5.1 导数的概念及其运算

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

选择性必修第二册同步拔高，难度2颗星！

模块导图

知识剖析

平均变化率

若某个问题中的函数关系用\(f(x)\)表示，问题中的变化率用式子\(\dfrac { Δ y } { Δx } = \dfrac { f ( x _ { 0 } + Δ x ) - f ( x _ { 0 } ) } { Δ x }\)表示，
则式子\(\dfrac{\Delta y}{\Delta x}\)称为函数\(f(x)\)从\(x_0\)到\(x_0+∆x\)的平均变化率.
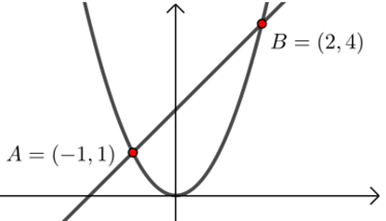
\({\color{Red}{ Eg }}\) 函数\(f(x)=x^2\)在区间\([－1 ,2]\)上的平均变化率为\(\dfrac{\Delta y}{\Delta x}=\dfrac{f(2)-f(-1)}{2-(-1)}=\dfrac{4-1}{3}=1\)．
它与斜率\(k_{AB}\)相等.

 

导数概念

函数\(f(x)\)在\(x=x_0\)处的瞬时变化率是

\[\lim _{\Delta x \rightarrow 0} \dfrac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \dfrac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} \]

则称它为函数\(y=f(x)\)在\(x=x_0\)处的导数，记作\(f'(x_0)\) 或\(y ^ { \prime } | _ { x = x _ { 0 } }\)，即

\[f^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0} \dfrac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \dfrac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x} \]

 

导函数

若当\(x\)变化时，\(f'(x)\)是\(x\)的函数，则称它为\(f(x)\)的导函数(简称导数)，记作\(f'(x)\)或\(y'\) ，即

\[f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \dfrac{f(x+\Delta x)-f(x)}{\Delta x} \]

 

基本初等函数的导数公式

 

导数运算法则

(1)\([ f ( x ) \pm g ( x ) ] ^ { \prime } = f ^ { \prime } ( x ) \pm g ^ { \prime } ( x )\)；
拓展：\([ f ( x ) \pm g ( x ) + \cdots \pm u ( x ) ] ^ { \prime } = f ^ { \prime } ( x ) \pm g ^ { \prime } ( x ) \pm \cdots\pm u ^ { \prime } ( x )\)；
记忆：函数的和差的导数等于函数导数的和差；
 
(2)\([ f ( x ) \cdot g ( x ) ] ^ { \prime } = f ^ { \prime } ( x ) g ( x ) + f ( x ) g ^ { \prime } ( x )\)；
特别：\([ C \cdot f ( x ) ] ^ { \prime } = C \cdot f ^ { \prime } ( x )\)，\(C\)为常数；
记忆：两函数积的导数等于“前导后不导＋后导前不导”；
 
(3)\(\left[\dfrac{f(x)}{g(x)}\right]^{\prime}=\dfrac{f^{\prime}(x) g(x)-f(x) g^{\prime}(x)}{[g(x)]^{2}}(g(x) \neq 0)\).
记忆：两函数商的导数等于“分母平分，分子导分母不导－分母导分子不导”.
 

复合函数的导数

对于两个函数\(y=f(u)\)和\(u=g(x)\)，若通过变量\(u ,y\) 可以表示成\(x\)的函数，则称这个函数为函数\(y=f(u)\)和\(u=f(x)\)的复合函数，记作\(y=f(g(x))\)．
复合函数\(y=f(g(x))\)的导数与函数\(y=f(u)\) ,\(u=f(x)\) 的导数间的关系是\(y _ { x } ^ { \prime } = y _ { u } ^ { \prime } \cdot u _ { x } ^ { \prime }\)．
\({\color{Red}{ Eg }}\) 若\(f(x)=ln⁡(x^2+2x+3)\)，设\(y=\ln u\)，\(u=x^2+2x+3\)
则\(f^{\prime}(x)=(\ln u)^{\prime} \cdot\left(x^{2}+2 x+3\right)\)\(=\dfrac{1}{u} \cdot(2 x+2)=\dfrac{2 x+2}{x^{2}+2 x+3}\).
 

经典例题

【题型一】导数概念的理解

【典题1】 函数\(y=x^2\)在区间\([x_0 ,x_0+∆x]\)上的平均变化率为\(k_1\)，在\([x_0－∆x ,x_0]\)上的平均变化率为\(k_2\)，则\(k_1\)与\(k_2\)的大小关系是(　　)
A．\(k_1>k_2\) \(\qquad \qquad\qquad \qquad \qquad \qquad\) B．\(k_1<k_2\)
C．\(k_1=k_2\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D．\(k_1 ,k_2\)大小关系不能确定
【解析】\(∵\)函数\(y=f(x)=x^2\)在\(x_0\)到\(x_0+∆x\)之间的平均变化量为：
\(∆y=f(x_0+∆x)－f(x_0)=(x_0+∆x)^2－(x_0 )^2=∆x(2x_0+∆x)\)
\(\therefore k_{1}=\dfrac{\Delta y}{\Delta x}=2 x_{0}+\Delta x\)．
\(∵\)函数\(y=f(x)=x^2\)在\(x_0－∆x\)到\(x_0\)之间的平均变化量为：
\(\Delta y=f\left(x_{0}\right)-f\left(x_{0}-\Delta x\right)=\left(x_{0}\right)^{2}-\left(x_{0}-\Delta x\right)^{2}=\Delta x\left(2 x_{0}-\Delta x\right)\)
\(\therefore k_{2}=\dfrac{\Delta y}{\Delta x}=2 x_{0}-\Delta x\)．
\(∵k_1－k_2=2∆x\)，而\(∆x>0\)，故\(k_1>k_2\)．
故选：\(A\)．
【点拨】平均变化率\(\dfrac{\Delta y}{\Delta x}=\dfrac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}\)，由二次函数的图象也易得\(k_1>k_2.\)
 

【典题2】 已知函数\(f(x)\)是可导函数，且\(f'(a)=1\)，则\(\lim _{x \rightarrow a} \dfrac{f(2 x-a)-f(2 a-x)}{x-a}\)等于\(\underline{\quad \quad}\)．
【解析】\(∵ f'(a)=1\)，\(\therefore \lim _{\left(x_{2}-x_{1}\right) \rightarrow 0} \dfrac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}=1\)，
设\(x_2=2x-a ,x_1=2a-x\)，
\(\begin{aligned} &\therefore \lim _{x \rightarrow a} \dfrac{f(2 x-a)-f(2 a-x)}{(2 x-a)-(2 a-x)}=1 \\ &\Rightarrow \lim _{x \rightarrow a} \dfrac{f(2 x-a)-f(2 a-x)}{3(x-a)}=1 \end{aligned}\)
\(\begin{aligned} &\Rightarrow \dfrac{1}{3} \cdot \lim _{x \rightarrow a} \dfrac{f(2 x-a)-f(2 a-x)}{x-a}=1 \\ &\Rightarrow \lim _{x \rightarrow a} \dfrac{f(2 x-a)-f(2 a-x)}{x-a}=3 \end{aligned}\)
故答案为：\(3\)．
【点拨】导数有不同表示形式
\(f^{\prime}(a)=\lim _{\Delta x \rightarrow 0} \dfrac{f(a+\Delta x)-f(a)}{\Delta x}\)\(=\lim _{x \rightarrow a} \dfrac{f(x)-f(a)}{x-a}\)\(=\lim _{\left(x_{2}-x_{1}\right) \rightarrow 0} \dfrac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}\) (\(x_2 ,x_1\)与\(x_0\)相关).
 

【典题3】 求\(\lim _{x \rightarrow 0} \dfrac{\sin x}{x}\).
【解析】设\(f(x)=sinx\)，由求导公式可知\(f^{\prime} (x)=cosx\)，
\(\lim _{x \rightarrow 0} \dfrac{\sin x}{x}\)
\(=\lim _{x \rightarrow 0} \dfrac{\sin x-\sin 0}{x-0}\) \({\color{Red}{(构造出导数的形式) }}\)
\(=\lim _{x \rightarrow 0} \dfrac{f(x)-f(0)}{x-0}\)
\(=f^{\prime}(0)\) \({\color{Red}{ (由导数的概念可知) }}\)
\(=1\)
【点拨】
① 用大学知识点洛必达法则可算出\(\lim _{x \rightarrow 0} \dfrac{\sin x}{x}=1\)；
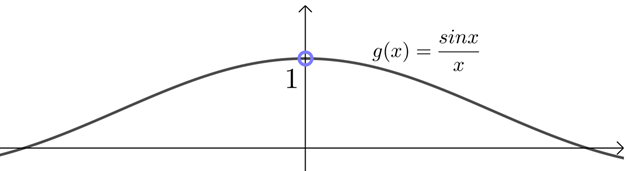
② 本题的实质：函数\(g(x)=\dfrac{\sin x}{x}\)在\(x=0\)处没意义，那当\(x⟶0\)时，\(g(x)\)趋向何值？在后面求函数值域时常要考虑，解析中由导数的概念也可得到\(y\)值趋向\(1\)，如下图.

 

巩固练习

1(★)函数\(f(x)=x\) ,\(g(x)=x^2\) ,\(h(x)=x^3\)在\([0 ,1]\)的平均变化率分别记为\(m_1\) ,\(m_2\) ,\(m_3\)，则下面结论正确的是(　　)
A．\(m_1=m_2=m_3\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B．\(m_1>m_2>m_3\)
C．\(m_2>m_1>m_3\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) D．\(m_1<m_2<m_3\)
 

2(★) 某物体做自由落体运动的位移\(s(t)=\dfrac{1}{2} gt^2\)，\(g=9.8m/s^2\)，若\(\lim _{\Delta t \rightarrow 0} \dfrac{s(1+\Delta t)-s(1)}{\Delta t}=9.8 \mathrm{~m} / \mathrm{s}\)，
则\(9.8m/s\)是该物体(　　)
A．从\(0 s\)到\(1 s\)这段时间的平均速度
B．从\(1 s\)到\((1+∆t)s\)这段时间的平均速度
C．在\(t=1 s\)这一时刻的瞬时速度
D．在\(t=∆t s\)这一时刻的瞬时速度
 

3(★★)设函数\(f(x)\)可导，\(f^{\prime} (1)=3\)，则\(\lim _{\Delta x \rightarrow 0} \dfrac{f(1+\Delta x)-f(1)}{3 \Delta x}=\) \(\underline{\quad \quad}\)．
 

4(★★) 已知\(f'(x)\)是\(f(x)\)的导函数，且\(f^{\prime} (1)=3\)，则\(\lim _{\Delta x \rightarrow 0} \dfrac{f(1)-f(1+2 \Delta x)}{\Delta x}=\) \(\underline{\quad \quad}\)．
 

5(★★★)求\(\lim _{x \rightarrow 0} \dfrac{e^{x}-1}{x}\).
 

参考答案

1. \(A\)
2. \(C\)
3. \(1\)
4. \(－6\)
5. \(1\)
    

【题型二】导数的运算

【典题1】 设函数\(f(x)\)的导函数是\(f^{\prime}(x)\)，若\(f(x)=f^{\prime}\left(\dfrac{\pi}{2}\right) \cdot \cos x-\sin x\)，则\(f^{\prime}(\dfrac{π}{3})=\) \(\underline{\quad \quad}\)
【解析】 \(∵f(x)=f^{\prime}\left(\dfrac{\pi}{2}\right) \cdot \cos x-\sin x\)，
\(\therefore f^{\prime}(x)=-f^{\prime}\left(\dfrac{\pi}{2}\right) \sin x-\cos x\)，
\({\color{Red}{( f^{\prime}(\dfrac{π}{2})是个常数) }}\)
\(\therefore f^{\prime}\left(\dfrac{\pi}{2}\right)=-f^{\prime}\left(\dfrac{\pi}{2}\right) \sin \dfrac{\pi}{2}-\cos \dfrac{\pi}{2}=-f^{\prime}\left(\dfrac{\pi}{2}\right)\)，
\(\therefore f^{\prime}\left(\dfrac{\pi}{2}\right)=0\)
\(∴f'(x)=－cosx\)，\(∴f^{\prime}(\dfrac{π}{3})=-\dfrac{1}{2}\).
 

【典题2】 求下列函数的导数：
\((1)y=(2x^2+3)(3x－1)\)；
\((2) y=2xtanx\)；
\((3)y=-2 \sin \dfrac{x}{2}\left(2 \sin ^{2} \dfrac{x}{4}-1\right)\)；
\((4)y=sin^2 (2x+\dfrac{π}{3})\)
【解析】(1) \({\color{Red}{方法一 }}\) \(∵y=(2x^2+3)(3x－1)\)，
\(\therefore y^{\prime}=\left(2 x^{2}+3\right)^{\prime}(3 x-1)+\left(2 x^{2}+3\right)(3 x-1)^{\prime}\)
\(=4x(3x－1)+3(2x^2+3)\)
\(=18x^2－4x+9\)；
\({\color{Red}{方法二 }}\) \(∵y=(2x^2+3)(3x－1)\)\(=6x^3-2x^2+9x-3\)
\(∴y^{\prime}=18x^2－4x+9\)
(2) \(\because y=2 x \tan x=2 \cdot \dfrac{x \sin x}{\cos x}\),
\({\color{Red}{(y=tanx没有求导公式tanx=\dfrac{ \sin x}{\cos x} )}}\)
\(\therefore y^{\prime}=2 \dfrac{(\sin x+x \cos x) \cos x-x \sin x(-\sin x)}{\cos ^{2} x}\)\(=\dfrac{2 \sin x \cos x+2 x}{\cos ^{2} x}\)\(=\dfrac{\sin 2 x+2 x}{\cos ^{2} x}\)．
(3)\(\because y=-2 \sin \dfrac{x}{2}\left(2 \sin ^{2} \dfrac{x}{4}-1\right)\)\(=2 \sin \dfrac{x}{2}\left(1-2 \sin ^{2} \dfrac{x}{4}\right)\)\(=2 \sin \dfrac{x}{2} \cos \dfrac{x}{2}=\sin x\)． \({\color{Red}{(先化简) }}\)
\(∴y'=(sin x)'=cos x\)．
(4) \({\color{Red}{ 方法一}}\) 由复合函数求导，可得
\(y^{\prime}=2 \sin \left(2 x+\dfrac{\pi}{3}\right) \cdot\left[\sin \left(2 x+\dfrac{\pi}{3}\right)\right]^{\prime}\)\(=2 \sin \left(2 x+\dfrac{\pi}{3}\right) \cos \left(2 x+\dfrac{\pi}{3}\right) \cdot 2\)\(=2 \sin \left(4 x+\dfrac{2 \pi}{3}\right)\)；
\({\color{Red}{ 方法二}}\) \(y=\sin ^{2}\left(2 x+\dfrac{\pi}{3}\right)\)\(=\dfrac{1-\cos \left(4 x+\dfrac{2 \pi}{3}\right)}{2}\)\(=\dfrac{1}{2}-\dfrac{1}{2} \cos \left(4 x+\dfrac{2 \pi}{3}\right)\)
\(\therefore y^{\prime}=0+\dfrac{1}{2} \cdot \sin \left(4 x+\dfrac{2 \pi}{3}\right) \cdot 4=2 \sin \left(4 x+\dfrac{2 \pi}{3}\right)\).
【点拨】求导先要明确函数的结构，是函数“加减形式”、“乘除形式”还是“复合函数形式”,再选择简单形式求导.
 

【典题3】 已知函数\(f(x)=\dfrac{(x+1)^{2}+\sin x}{x^{2}+1}\)，其中\(f^{\prime}(x)\)为函数\(f(x)\)的导数，则\(f(2020)+ f(－2020)+f'(2019)－f'(－2019)=\) \(\underline{\quad \quad}\)
【解析】 \({\color{Red}{方法一 }}\) \(\because f(x)=\dfrac{(x+1)^{2}+\sin x}{x^{2}+1}\)\(=\dfrac{2 x+\sin x}{x^{2}+1}+1\)
设\(g(x)=\dfrac{2 x+\sin x}{x^{2}+1}\)，则\(g(x)\)是奇函数，\(g(x)+g(-x)=0\),
\(∴f(x)+f(－x)=g(x)+g(-x)+2=2\)\(⟹f(2020)+f(－2020)=2\)
\(\because f^{\prime}(x)=\dfrac{(\cos x+2)\left(x^{2}+1\right)-2 x(2 x+\sin x)}{\left(x^{2}+1\right)^{2}}\)\(=\dfrac{x^{2} \cos x+\cos x-2 x^{2}+2 x \sin x+2}{\left(x^{2}+1\right)^{2}}\)是偶函数；
\(∴f^{\prime}(2019)－f^{\prime}(－2019)=0\)；
\(∴f(2020)+f(－2020)+f'(2019)－f'(－2019)=2\)．
\({\color{Red}{ 方法二}}\) \(\because f(x)=\dfrac{(x+1)^{2}+\sin x}{x^{2}+1}\)\(=\dfrac{2 x+\sin x}{x^{2}+1}+1\)
设\(g(x)=\dfrac{2 x+\sin x}{x^{2}+1}\)，则\(g(x)\)是奇函数，\(g(x)+g(-x)=0\),
\(∴f(x)+f(－x)=g(x)+g(-x)+2=2\)\(⟹f(2020)+f(－2020)=2\)
\(∵g(x)\)是奇函数，\(∴g'(x)\)是偶函数，\(∴f^{\prime} (x)\)是偶函数
\(∴f^{\prime} (2019)－f^{\prime} (－2019)=0\)；
\(∴f(2020)+f(－2020)+f'(2019)－f'(－2019)=2\).
【点拨】
① 函数奇偶性的判断：奇+奇=奇，偶+偶=偶，奇×奇=偶，奇×偶=奇，偶×偶=偶；了解这些能更快判断复杂函数的奇偶性；
② 奇函数的导数是偶函数，偶函数的导数是奇函数.
 

【典题4】 设\(f(x)=x(x-1)(x-2)(x-3)……(x-99)\)，则\(f'(0)=\) \(\underline{\quad \quad}\) .
【解析】
\({\color{Red}{ 方法一}}\) \(∵f(x)=x\cdot [(x-1)(x-2)(x-3)……(x-99)]\)
\(∴f^{\prime}(x)=[(x-1)(x-2)(x-3)……(x-99)]\)\(+x\cdot [(x-1)(x-2)(x-3)……(x-99)]\)
\(∴f^{\prime}(0) =-99!+0=-99!\).
\({\color{Red}{ 方法二}}\) \(f(x)=x(x-1)(x-2)(x-3)……(x-99)\)
\(∴f(x)=a_{100} x^{100}+a_{99} x^{99}+⋯+a_2 x^2+(-1)\cdot(-2)\cdot(-3)\cdot \cdot \cdot(-99)x\)
\(∴f^{\prime} (x)=100a_{100} x^{99}+99a_{99} x^{98}+⋯+2a_2 x-99!\)
\(∴f'(0)=-99!.\)
 

【典题5】 写出\(g(x)\)与\(f(x)\)的一种关系.
\((1)\)若\(f^{\prime} (x)+2x-3>0\)，则\(g^{\prime}(x)>0\)
\((2)\)若\(xf^{\prime}(x)+f(x)>0\)，则\(g^{\prime}(x)>0\)
\((3)\)若\(f^{\prime}(x)+f(x)>0\)，则\(g^{\prime}(x)>0\) .
\((4)\)若\(xf^{\prime}(x)+2f(x)>0(x>0)\)，则\(g^{\prime}(x)>0\)
\((5)\)若\(f^{\prime}(x)\cdot lnx+\dfrac{1}{x}\cdot f(x)>0\)，则\(g^{\prime}(x)>0\)
\((6)\)若\(xf^{\prime} (x)-f(x)>0\)，则\(g^{\prime}(x)>0\)
\((7)\)若\(f^{\prime} (x)-f(x)>0\)，则\(g^{\prime}(x)>0\)
【解析】
\((1)g(x)=f(x)+x^2-3x\)
\({\color{red} {对应[f(x)± g(x)]^{\prime}=f^{\prime} (x)±g^{\prime}(x)}}\)
\((2)g(x)=xf(x)\) \((3)g(x)=e^x f(x)\)
\((4) g(x)=x^2 f(x)\) \((5)g(x)=lnx\cdot f(x)\)
\({\color{red} {2-5题对应[f(x)⋅g(x)]^{\prime}=f^{\prime} (x) g(x)+f(x) g^{\prime} (x)}}\)
\((6) g(x)=\dfrac{f(x)}{x}\) \((7) g(x)=\dfrac{f(x)}{e^{x}}\)
\({\color{red} {6,7题对应\left[\dfrac{f(x)}{g(x)}\right]^{\prime}=\dfrac{f^{\prime}(x) g(x)-f(x) g^{\prime}(x)}{[g(x)]^{2}}(g(x) \neq 0)}}\)
【点拨】这是导数运算法则的逆运用，也是后面的一种构造函数的技巧，注意函数的结构灵活运用导数运算公式.
 

巩固练习

1(★)若函数\(f(x)\)满足\(f(x)=\dfrac{1}{3} x^3-f'(1)⋅x^2-x\)，则\(f'(0)\)的值为\(\underline{\quad \quad}\)．
 

2(★)已知函数\(f(\theta)=\dfrac{\sin \theta}{2+\cos \theta}\)，则\(f'(0)=\) \(\underline{\quad \quad}\)．
 

3(★)已知函数\(f(x)=\ln \left(x+\sqrt{1+x^{2}}\right)\)，则\(f'(3)=\) \(\underline{\quad \quad}\)
 

4(★★)已知函数\(f(x)=e^x-cosx\)，设\(f_0 (x)=f^{\prime}(x) ,f_{k+1} (x)=f_k^{\prime} (x)(k∈N)\)，则\(f_{2014} (0)\)的值为\(\underline{\quad \quad}\)．
 

5(★★)求下列函数的导数：
\((1)f(x)=(3x^2+1)(2－x)\)
\((2)f(x)=x^2 ln(2x)\)
\((3)f(x)=ln(2x－1)^3\)．
 

6(★★★)求\(\lim \limits _{x \rightarrow 1} \dfrac{2 x \ln x}{1-x^{2}}\).
 
 

7(★★★)记函数\(f(x)\)的导数为\(f^{1} (x)\)，\(f^{1} (x)\)的导数为\(f^{2} (x)\)，…，\(f^{n-1} (x)\)的导数为\(f^{n} (x)\)，若\(f(x)\)可进行\(n\)次求导，则\(f(x)\)均可近似表示为：\(f(x) \approx f(0)+\dfrac{f^{(1)}(0)}{1 !} x+\dfrac{f^{(2)}(0)}{2 !} x^{2}\)\(+\dfrac{f^{(3)}(0)}{3 !} x^{3}+\cdots+\dfrac{f^{(n)}(0)}{n !} x^{n}\)，若取\(n=4\)，根据这个结论，则可近似估计\(cos2≈\) \(\underline{\quad \quad}\) (用分数表示)．
 
 

答案

1. \(-1\)

2. \(\dfrac{1}{3}\)

3. \(\dfrac{\sqrt{10}}{10}\)

4. \(1\)

5. \((1)f'(x)=－9x^2+12x－1\)；
   \((2)f'(x)=x(2ln2x+1)\)；
   \((3) f^{\prime}(x)=\dfrac{6}{2 x-1}\)

6. \(-1\)

7. \(-\dfrac{1}{3}\)