2.1 一元二次函数、方程和不等式

\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步拔高，难度3颗星！

模块导图

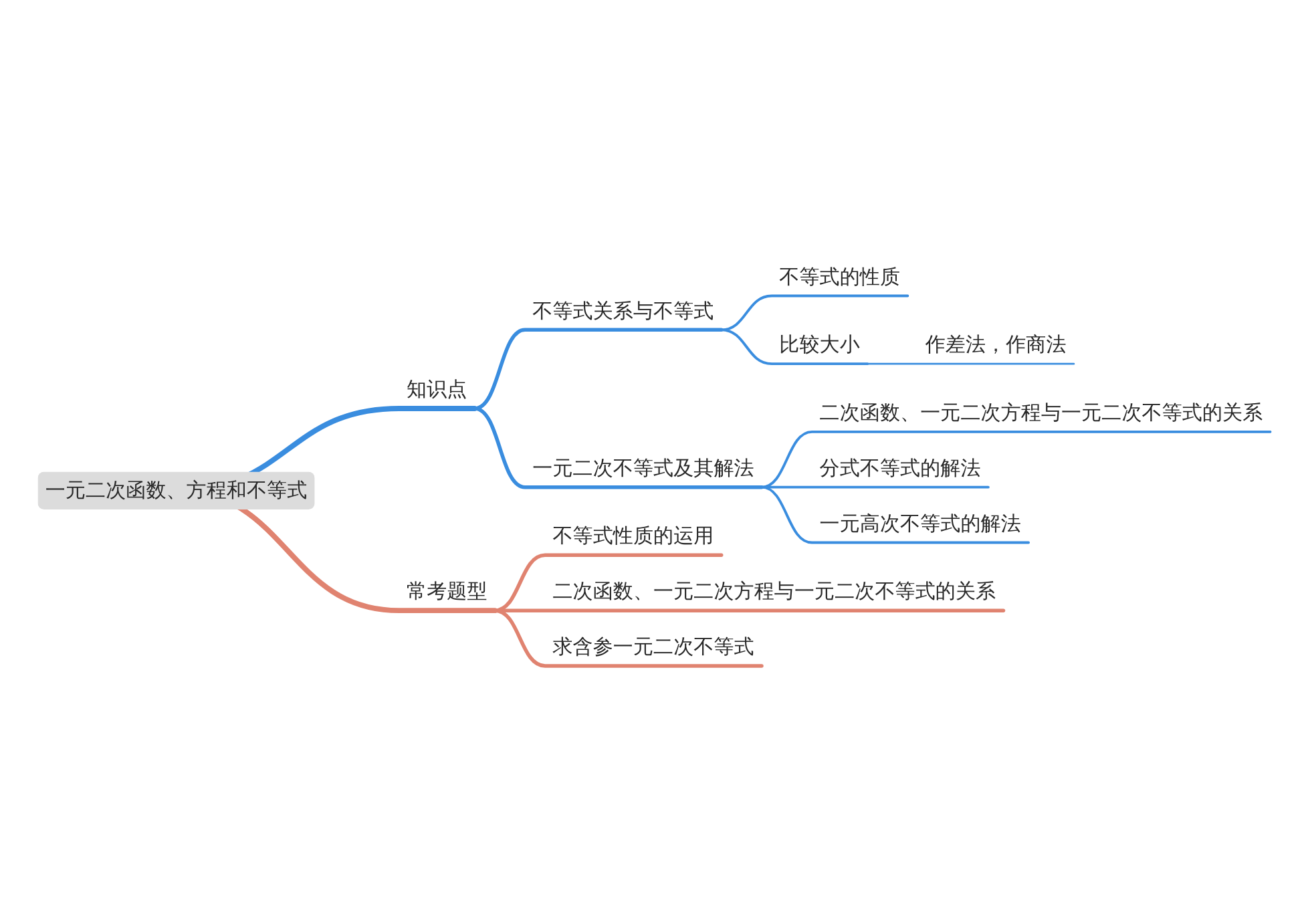
知识剖析

不等式关系与不等式

1 不等式的性质
\((1)\)传递性：\(a>b ,b>c⇒ a>c\)；
\((2)\)加法法则：\(a>b ⇒ a+c>b+c\),\(a>b ,c>d ⇒ a+c>b+d\)；
\((3)\)乘法法则：\(a>b ,c>0 ⇒ ac>bc\),\(a>b ,c<0⇒ac<b c\)；
\((4)\)倒数法则：\(a>b, a b>0 \Rightarrow \dfrac{1}{a}<\dfrac{1}{b}\)；
\((5)\)乘方法则：\(a>b>0 \Rightarrow a^{n}>b^{n}\)(\(n∈ N^*\)且\(n>1\))；
 

2 比较\(a ,b\)大小
\((1)\)作差法(\(a-b\)与\(0\)的比较)
\(a-b>0\Rightarrow a>b\);\(a-b=0\Rightarrow a=b\);\(a-b<0\Rightarrow a<b\)

\((2)\)作商法(\(\dfrac{a}{b}\)与\(1\)比较)
\(\dfrac{a}{b}>1, b>0 \Rightarrow a>b\)；\(\dfrac{a}{b}>1, b<0 \Rightarrow a<b\)
 

一元二次不等式及其解法

1二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系：
(以下均以为例)

 
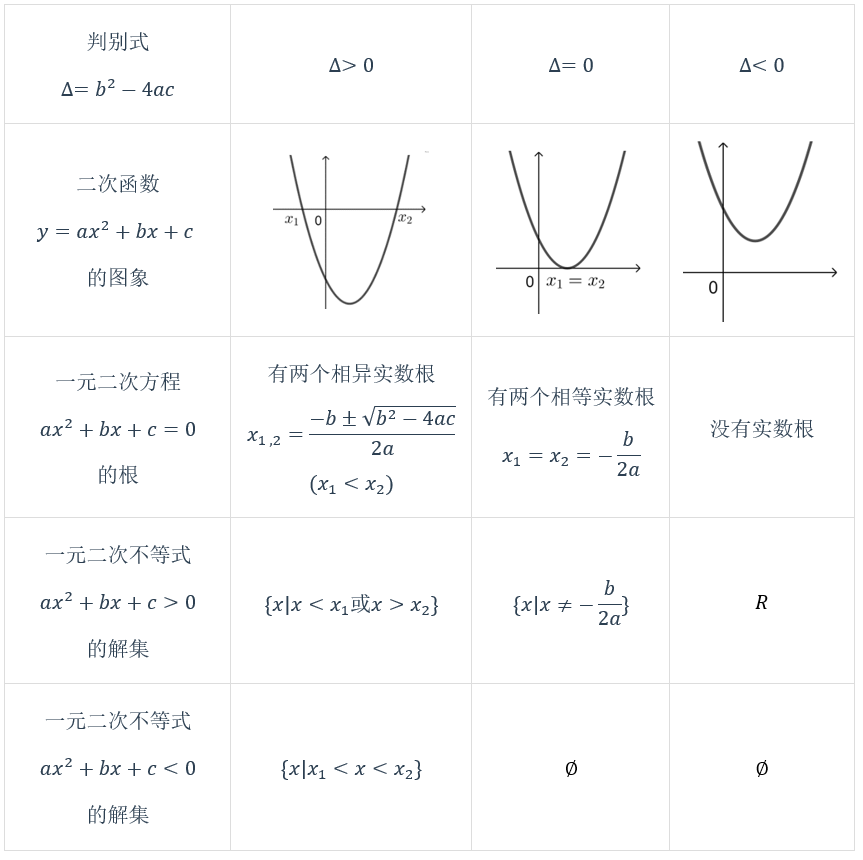
2二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系，可充分利用二次函数图像去理解；

3求解一元二次不等式时，利用二次函数图像思考，需要确定二次函数的开口方向，判别式，两根的大小与不等式的解集有关，而对称轴是不会影响解集的.

一元二次不等式的应用

1 分式不等式的解法
解分式不等式可等价为有理整式不等式(组)求解.
由于\(\dfrac{a}{b}>0\)与\(ab>0\)均意味\(a,b\)同号，
故\(\dfrac{a}{b}>0\)与\(ab>0\)等价的；
\(\dfrac{a}{b}<0\)与\(ab<0\)均意味\(a,b\)异号，
故\(\dfrac{a}{b}<0\)与\(ab<0\)等价的；
可得①\(\dfrac{f(x)}{g(x)}>0 \Rightarrow f(x) g(x)>0\)，\(\dfrac{f(x)}{g(x)} \geq 0 \Rightarrow f(x) g(x) \geq 0\)且\(g(x)≠0\).
\({\color{Red}{ Eg }}\)\(\dfrac{x-1}{x-2}>0 \Rightarrow(x-1)(x-2)>0\);\(\dfrac{x-1}{x-2} \leq 0 \Rightarrow(x-1)(x-2) \leq 0\)且\(x-2≠0\).
②\(\dfrac{f(x)}{g(x)}<0 \Rightarrow f(x) g(x)<0\)，\(\dfrac{f(x)}{g(x)} \leq 0 \Rightarrow f(x) g(x) \leq 0\)且\(g(x)≠0\).

\({\color{Red}{ Eg }}\)\(\dfrac{x-1}{x-2}<0 \Rightarrow(x-1)(x-2)<0\);\(\dfrac{x-1}{x-2} \leq 0 \Rightarrow(x-1)(x-2) \leq 0\)且\(x-2≠0\).
 

2 一元高次不等式的解法
① 一元高次不等式通常先进行因式分解，化为\((x-x_1 )(x-x_2 )…(x-x_n )>0\)(或\(<0\))的形式，然后用穿针引线法求解.首先保证每个因式中\(x\)的系数为正，然后从右侧画起，右侧第一个区间为正，从右向左依次正负出现，特别要注意“奇穿偶切”，“奇”(“偶”)指的是某个因式的次数.
\({\color{Red}{ Eg }}\)
解\((x+1)(x-2)(x-3)(x-4)≥0\)，如图所示，解集为\(\{x|x≥4或2≤x≤3或x≤-1\}\).

解\((x+1) (x-2)^2 (x-3) (x-4)^3≤0\)，如图所示，解集为\(\{x|x≤-1或x=2或3≤x≤4\}\).

 

经典例题

【题型一】不等式性质的运用

【典题1】实数\(a、b、c\)满足\(a>b>c\)，则下列不等式正确的是 (　　)
A．\(a+b>c\) \(\qquad \qquad\) B．\(\dfrac{1}{a-c}<\dfrac{1}{b-c}\)\(\qquad \qquad\) C．\(a|c|>b|c|\) \(\qquad \qquad\)D．\(\dfrac{a b^{2}}{c^{2}+1}<\dfrac{a^{2} b}{c^{2}+1}\)
【解析】\(∵a>b>c\)，
\(∴\)对于\(A\)，\(a+b>c\)错误，比如\(-4>-5>-6\)，得出\(-4+(-5)<-6\)；
对于\(B\)．\(a-c>b-c>0\)，\(\therefore \dfrac{1}{a-c}<\dfrac{1}{b-c}\)，\(∴\)该选项正确；
对于\(C\)．\(a|c|>b|c|\)错误，
比如\(|c|=0\)时，\(a|c|=b|c|\)；
对于\(D\)．\(∵a b^{2}-a^{2} b=a b(b-a)\)，
\(∴a b(b-a)=0\)时，\(a b^{2}=a^{2} b\)，
\(\therefore \dfrac{a b^{2}}{c^{2}+1}=\dfrac{a^{2} b}{c^{2}+1}\)，\(∴\)该选项错误．
故选：\(B\)．
【点拨】涉及不等式的选择题，适当利用“取特殊值排除法”会做得更快些.
 

【典题2】已知\(a>0\)，试比较\(\dfrac{a^{2}+1}{a^{2}-1}\)与\(\dfrac{a+1}{a-1}\)的值的大小．
【解析】\(\dfrac{a^{2}+1}{a^{2}-1}-\dfrac{a+1}{a-1}=\dfrac{a^{2}+1-(a+1)^{2}}{a^{2}-1}=\dfrac{-2 a}{a^{2}-1}\)， \({\color{Red}{(作差法) }}\)
\((i)\)当\(a>1\)时，\(-2a<0\)，\(a^2-1>0\)，
则\(\dfrac{-2 a}{a^{2}-1}<0\)；
\({\color{Red}{ (确定差\dfrac{-2 a}{a^{2}-1}与0的大小)}}\)
即\(\dfrac{a^{2}+1}{a^{2}-1}<\dfrac{a+1}{a-1}\)
\((ii)\)当\(0<a<1\)时，\(-2a<0\),\(a^2-1<0\)，
则\(\dfrac{-2 a}{a^{2}-1}>0\)；即\(\dfrac{a^{2}+1}{a^{2}-1}>\dfrac{a+1}{a-1}\)．
综上可得\(a>1\)时，\(\dfrac{a^{2}+1}{a^{2}-1}<\dfrac{a+1}{a-1}\)；
\(0<a<1\)时，\(\dfrac{a^{2}+1}{a^{2}-1}>\dfrac{a+1}{a-1}\)．
【点拨】比较两个式子的大小，可用做差法或做商法；一般幂的形式比较大小用作商法，比如比较\(a^{a} b^{b}\)与\((a b)^{\frac{a+b}{2}}\)；多项式形式常用做差法，比如比较\(xy\)与\(x+y-1\).
 

【典题3】已知\(C>1\)，\(a=\sqrt{C+1}-\sqrt{C}\)，\(b=\sqrt{C}-\sqrt{C-1}\)，则正确的结论是(　　)
A．\(a<b\) \(\qquad \qquad \qquad \qquad\)B．\(a>b\)\(\qquad \qquad \qquad \qquad\)C\(．a=b\)\(\qquad \qquad \qquad \qquad\) D．\(a\)与\(b\)的大小不确定
【解析】 \({\color{Red}{方法一 \quad 特殊值法 }}\)
取特殊值，令\(c=2\)，
则\(a=\sqrt{3}-\sqrt{2}\)，\(b=\sqrt{2}-1\)，
易知\(a<b\), 排除\(B,C\)，还不能排除\(D\)，猜测选\(A\).
\({\color{Red}{方法二 \quad 做差法，分析法 }}\)
\(a-b=\sqrt{c+1}-\sqrt{c}-(\sqrt{c}-\sqrt{c-1})\)\(=\sqrt{c+1}+\sqrt{c-1}-2 \sqrt{c}\)
要比较\(a ,b\)大小，
只需要比较\(\sqrt{c+1}+\sqrt{c-1}\)与\(2 \sqrt{c}\)的大小
\(\Leftrightarrow\)比较\((\sqrt{c+1}+\sqrt{c-1})^{2}\)与\(4c\)的大小
\({\color{Red}{(遇到二次根式可考虑平方去掉根号) }}\)
\(\Leftrightarrow\)比较\(2 c+2 \sqrt{c^{2}-1}\)与\(4c\)的大小
\(\Leftrightarrow\)比较\(\sqrt{c^{2}-1}\)与\(c\)的大小
而显然\(\sqrt{c^{2}-1}<c\)，
故\(\sqrt{c+1}+\sqrt{c-1}<2 \sqrt{c}\)，故\(a<b\)，故选\(A\).
\({\color{Red}{ 方法三 \quad 共轭根式法}}\)
\(\sqrt{c+1}-\sqrt{c}=\dfrac{(\sqrt{c+1}-\sqrt{c})(\sqrt{c+1}+\sqrt{c})}{\sqrt{c+1}+\sqrt{c}}=\dfrac{1}{\sqrt{c+1}+\sqrt{c}}\)\(\sqrt{c}-\sqrt{c-1}=\dfrac{(\sqrt{c}-\sqrt{c-1})(\sqrt{c}+\sqrt{c-1})}{\sqrt{c}+\sqrt{c-1}}=\dfrac{1}{\sqrt{c}+\sqrt{c-1}}\)，
\(∵c>1\)，
\(\therefore c+1>c-1>0 \Rightarrow \sqrt{c+1}>\sqrt{c-1}\)\(\Rightarrow \sqrt{c+1}+\sqrt{c}>\sqrt{c}+\sqrt{c-1}>0\)，
\(\therefore \dfrac{1}{\sqrt{c+1}+\sqrt{c}}<\dfrac{1}{\sqrt{c}+\sqrt{c-1}}\)，即\(a<b\)，故选\(A\).
【点拨】
① 比较两个式子的方法很多，选择题可以考虑取特殊值排除法；
② 方法二中，遇到带有根号的常常两边平方去掉根号再比较，此时注意两个式子是否都是正数；在思考的过程中，不断使用“等价转化”把比较的两个式子越化越简单，等价过程中注意严谨；
③ 方法三中注意到\((\sqrt{c}-\sqrt{c-1})(\sqrt{c}+\sqrt{c-1})=1\).
若\(A=\sqrt{x}+\sqrt{y}\)，\(B=\sqrt{x}-\sqrt{y}\)，\(A,B\)互为共轭根式，它们的乘积、平方和差有一定的特点.
\(A B=x-y\)，\(A^{2}+B^{2}=2(x+y)\)，\(A^{2}-B^{2}=4 \sqrt{x y}\).
 

巩固练习

1 (★) 已知\(-1<b<0\),\(a<0\)，那么下列不等式成立的是(　　)
A．\(a>ab>ab^2\) \(\qquad \qquad\)B．\(ab^2>ab>a\) \(\qquad \qquad\)C．\(ab>a>ab^2\) \(\qquad \qquad\)D．\(ab>ab^2>a\)
 

2(★★)设\(\dfrac{1}{b}<\dfrac{1}{a}<0\)，则下列不等式恒成立的是(　　)
A．\(a>b\) \(\qquad \qquad \qquad\) B．\(\dfrac{a}{b}<a-b\) \(\qquad \qquad \qquad\) C．\(\dfrac{b^{3}}{a^{3}}+\dfrac{a^{3}}{b^{3}}>2\)\(\qquad \qquad \qquad\)D．\(\dfrac{1}{|b|}<\dfrac{1}{|a|}\)
 

3(★★)已知\(a ,b∈R\)，且\(P=\dfrac{a+b}{2}\)，\(Q=\sqrt{\dfrac{a^{2}+b^{2}}{2}}\)，则\(P、Q\)的关系是(　　)
A．\(P≥Q\) \(\qquad \qquad \qquad \qquad\)B．\(P>Q\) \(\qquad \qquad \qquad \qquad\)C．\(P≤Q\) \(\qquad \qquad \qquad \qquad\)D．\(P<Q\)
 

4(★★)若\(P=\sqrt{a+3}+\sqrt{a+5}\)，\(Q=\sqrt{a+1}+\sqrt{a+7}(a \geq 0)\)，则\(P，Q\)的大小关系是(　　)
A．\(P=Q\)\(\qquad \qquad \qquad \qquad\) B．\(P>Q\)\(\qquad \qquad \qquad \qquad\)C．\(P<Q\) \(\qquad \qquad \qquad \qquad\)D．由\(a\)的取值确定
 

5(★★★)设\(S=\dfrac{a}{a+b+c}+\dfrac{b}{b+c+d}\)\(+\dfrac{c}{c+d+a}+\dfrac{d}{d+a+b}\),\(a ,b ,c ,d∈R^+\)，则下列判断中正确的是(　　)
A．\(0<S<1\)\(\qquad \qquad \qquad\)B．\(1<S<2\)\(\qquad \qquad \qquad\)C．\(2<S<3\)\(\qquad \qquad \qquad\)D．\(3<S<4\)
 

答案

1.\(D\)
2.\(C\)
3.\(C\)
4.\(B\)
5.\(B\)

 

【题型二】二次函数、一元二次方程与一元二次不等式的关系

【典题1】如果关于\(x\)的不等式\(ax^2+bx+c>0\)的解集为\(-1<x<2\)，则关于\(x\)的不等式\(bx^2-ax-c>0\)的解集为\(\underline{\quad \quad}\).
【解析】关于\(x\)的不等式\(ax^2+bx+c>0\)的解集为\(-1<x<2\)，
\(∴-1、2\)是方程\(ax^2+bx+c=0\)的两实数根，且\(a<0\)，
由韦达定理得\(\left\{\begin{array}{l} -1+2=-\dfrac{b}{a} \\ -1 \times 2=\dfrac{c}{a} \end{array}\right.\)，
\(∴b=-a>0\),\(c=-2a>0\)，
\(∴\)不等式\(b x^{2}-a x-c>0\)化为\(-ax^2-ax+2a>0⇒x^2+x-2>0\)，
即\((x-1)(x+2)>0\)，解得\(x<-2\)或\(x>1\)；
则该不等式的解集为\((-∞ ,-2)∪(1 ,+∞)\)．
【点拨】通过二次函数的图像理解，二次函数、一元二次方程和一元二次不等式三者之间的关系.
 

【典题2】解关于\(x\)的不等式：\(\dfrac{x-2}{x+3} \geq 2\)
【解析】\(\dfrac{x-2}{x+3}-2 \geq 0 \Rightarrow \dfrac{x-2-2(x+3)}{x+3} \geq 0\)
\(\Rightarrow \dfrac{-x-8}{x+3} \geq 0 \Rightarrow \dfrac{x+8}{x+3} \leq 0\)；
等价变形为\((x+8)(x+3)≤0\)且\(x+3≠0\)
\({\color{Red}{(注意分母x+3≠0) }}\)
解得\(-8≤x<-3\).
 

巩固练习

1(★)若不等式\(2 k x^{2}+k x-\dfrac{3}{8}<0\)对一切实数\(x\)都成立，则\(k\)的取值范围为 (　　)
A．\(-3<k<0\) \(\qquad \qquad\) B．\(-3≤k<0\) \(\qquad \qquad\) C．\(-3≤k≤0\) \(\qquad \qquad\) D．\(-3<k≤0\)
 

2(★★)若关于\(x\)的不等式\(x^2-3ax+2>0\)的解集为\((-∞ ,1)∪(m ,+∞)\)，则\(a+m\)等于(　　)
A．\(-1\) \(\qquad \qquad \qquad \qquad\) B．\(1\) \(\qquad \qquad \qquad \qquad\) C．\(2\) \(\qquad \qquad \qquad \qquad\) D．\(3\)
 

3(★★)若不等式\(ax^2+2x+c<0\)的解集是\(\left(-\infty,-\dfrac{1}{3}\right) \cup\left(\dfrac{1}{2},+\infty\right)\)，则不等式\(cx^2-2x+a≤0\)的解集是(　　)
A．\(\left[-\dfrac{1}{2}, \dfrac{1}{3}\right]\) \(\qquad \qquad\) B．\(\left[-\dfrac{1}{3}, \dfrac{1}{2}\right]\) \(\qquad \qquad\) C．\([-2,3]\) \(\qquad \qquad\) D．\([-3 ,2]\)
 

4(★★)【多选题】关于\(x\)的一元二次不等式\(x^2-6x+a≤0(a∈Z)\)的解集中有且仅有\(3\)个整数，则\(a\)的取值可以是(　　)
A．\(6\) \(\qquad \qquad \qquad \qquad\) B．\(7\) \(\qquad \qquad \qquad \qquad\) C．\(8\) \(\qquad \qquad \qquad \qquad\) D．\(9\)
 

5(★★)不等式\(\dfrac{3 x+1}{3-x}>-1\)的解集是\(\underline{\quad \quad}\).
 

6(★★)已知不等式\(ax^2+bx+c>0\)的解集是\(\{x \mid \alpha<x<\beta\}\)，\(\alpha>0\)，则不等式\(cx^2+bx+a>0\)的解集是\(\underline{\quad \quad}\) .
 

7(★★)不等式\(\dfrac{a x}{x-1}<1\)的解集为\(\{x|x<1或x>2\}\)，则\(a\)值是 \(\underline{\quad \quad}\).
 

参考答案

1.\(D\)
2.\(D\)
3.\(C\)
4.\(ABC\)
5.\((-2，3)\)
6.\(\left(\dfrac{1}{\beta}, \dfrac{1}{\alpha}\right)\)
7.\(a=\dfrac{1}{2}\)
 

【题型三】求含参一元二次不等式

角度1：按二次项的系数\(a\)的符号分类，即\(a>0\),\(a=0\),\(a<0\);
解不等式\(ax^2+(a+2) x+1>0\).
【解析】
\({\color{Red}{ (不确定不等式对应函数y=ax^2+(a+2) x+1是否是二次函数，分a=0与a≠0讨论)}}\)
\((1)\)当\(a=0\)时，不等式为\(2x+1>0\)，解集为\(\left\{x \mid x>-\dfrac{1}{2}\right\}\)；
\((2)\)当\(a≠0\)时，\(\because \Delta=(a+2)^{2}-4 a=a^{2}+4>0\)
\({\color{Red}{ (二次函数y=ax^2+(a+2) x+1与x轴必有两个交点)}}\)
解得方程\(ax^2+(a+2) x+1=0\)两根\(x_{1}=\dfrac{-a-2-\sqrt{a^{2}+4}}{2 a}\)，\(x_{2}=\dfrac{-a-2+\sqrt{a^{2}+4}}{2 a}\)；
\({\color{Red}{(二次函数的开口方向与不等式的解集有关，分a>0与a<0讨论) }}\)
\((i)\)当\(a>0\)时，解集为\(\left\{x \mid x>\dfrac{-a-2+\sqrt{a^{2}+4}}{2 a} \text { 或 } x<\dfrac{-a-2-\sqrt{a^{2}+4}}{2 a}\right\}\)；
\((ii)\)当\(a<0\)时, 解集为\(\left\{x \mid \dfrac{-a-2+\sqrt{a^{2}+4}}{2 a}<x<\dfrac{-a-2-\sqrt{a^{2}+4}}{2 a}\right\}\).
\({\color{Red}{(注意x_1,x_2的大小) }}\)
综上，当\(a=0\)时，解集为\(\left\{x \mid x>-\dfrac{1}{2}\right\}\)；
当\(a>0\)时，解集为\(\left\{x \mid x>\dfrac{-a-2+\sqrt{a^{2}+4}}{2 a} \text { 或 } x<\dfrac{-a-2-\sqrt{a^{2}+4}}{2 a}\right\}\)；
当\(a<0\)时, 解集为\(\left\{x \mid x>\dfrac{-a-2+\sqrt{a^{2}+4}}{2 a} \text { 或 } x<\dfrac{-a-2-\sqrt{a^{2}+4}}{2 a}\right\}\).
 

角度2：按判别式的符号分类
解不等式\(x^2+ax+4>0\).
【解析】\(∵Δ=a^2-16\)
\({\color{Red}{(此时不确定二次函数y=x^2+ax+4是否与x轴有两个交点，对判别式进行讨论) }}\)
\(∴\)①当\(-4<a<4\)，即\(Δ<0\)时，解集为\(R\)；
②当\(a=±4\)，即\(Δ=0\)时，解集为\(\left\{x \mid x \neq-\dfrac{a}{2}\right\}\)；
③当\(a>4\)或\(a<-4\)，即\(Δ>0\)时，
此时两根为\(x_{1}=\dfrac{-a+\sqrt{a^{2}-16}}{2}\)，\(x_{2}=\dfrac{-a-\sqrt{a^{2}-16}}{2}\)，显然\(x_1>x_2\)，
\(∴\)不等式的解集为\(\left\{x \mid x>\dfrac{-a+\sqrt{a^{2}-16}}{2} \text { 或 } x<\dfrac{-a-\sqrt{a^{2}-16}}{2}\right\}\).
综上，当\(-4<a<4\)时，解集为\(R\)；

当\(a=±4\)时，解集为a>4；

当\(a>4\)或\(a<-4\)时，解集为\(\left\{x \mid x>\dfrac{-a+\sqrt{a^{2}-16}}{2} \text { 或 } x<\dfrac{-a-\sqrt{a^{2}-16}}{2}\right\}\).
 

角度3：按方程的根大小分类
解不等式\(x^{2}-\left(a+\dfrac{1}{a}\right) x+1<0\)\((a≠ 0)\).
【解析】原不等式可化为：\((x-a)\left(x-\dfrac{1}{a}\right)<0\),
令\((x-a)\left(x-\dfrac{1}{a}\right)=0\)，得\(x_{1}=a\)，\(x_{2}=\dfrac{1}{a}\)
\({\color{Red}{(因式分解很关键，此时确定y=(x-a)\left(x-\dfrac{1}{a}\right)与x轴有交点， x_1,x_2的大小影响不等式解集) }}\)
\(∴(i)\)当\(x_1=x_2\)时，即\(a=\dfrac{1}{a} \Rightarrow a=\pm 1\)时，解集为\(\varnothing\)；
\((ii)\)当\(x_1<x_2\)时，即\(a<\dfrac{1}{a} \Rightarrow a<-1\)或\(0<a<1\)时，解集为\(\left\{x \mid a<x<\dfrac{1}{a}\right\}\)；
\((iii)\)当\(x_1>x_2\)时，即\(a>\dfrac{1}{a} \Rightarrow-1<a<0\)或\(a>1\)时，解集为\(\left\{x \mid \dfrac{1}{a}<x<a\right\}\).
综上，当\(a=±1\)时，解集为\(\varnothing\)；
\((ii)\)当\(a<-1\)或\(0<a<1\)时，解集为\(\left\{x \mid a<x<\dfrac{1}{a}\right\}\)；
\((iii)\)当\(-1<a<0\)或\(a>1\)时， 解集为\(\left\{x \mid \dfrac{1}{a}<x<a\right\}\).
【点拨】
① 当求解一元二次不等式时，它是否能够因式分解，若可以就确定对应的二次函数与\(x\)轴有交点，就不需要考虑判别式.
常见的形式有\(x^{2}-(a+1) x+a=(x-1)(x-a)\),\(x^{2}-\left(a+\dfrac{1}{a}\right) x+1=(x-a)\left(x-\dfrac{1}{a}\right)\)，
\(ax^2+(a+1)x+1=(ax+1)(x+1)\)等，若判别式Δ是一个完全平方式，它就能做到“较好形式的十字相乘”，当然因式分解也可以用公式法求解；
② 在求解含参的一元二次不等式，需要严谨，多从二次函数的开口方向、判别式、两根大小的比较三个角度进行分类讨论，利用图像进行分析.
 

巩固练习

1(★★) 关于x的不等式\(x^2-(a+1)x+a<0\)的解集中恰有\(1\)个整数，则实数\(a\)的取值范围是 (　　)
A．\((-1 ,0]∪[2 ,3)\) \(\qquad \qquad\) B．\([-2 ,-1)∪(3 ,4]\) \(\qquad \qquad\) C．\([-1 ,0)∪( 2 ,3]\) \(\qquad \qquad\) D．\((-2 ,-1)∪(3 ,4)\)
 

2(★★) 解关于\(x\)的不等式\(x^2+2x+a>0\)．
 
 

3(★★)解关于\(x\)的不等式：\(2x^2+ax+2>0(a∈R)\)．
 
 

4(★★★)若\(a∈R\)，解关于\(x\)的不等式\(ax^2+(a+1)x+1>0\)．

 
 
5(★★★)关于\(x\)的不等式\((a x-1)^{2}<x^{2}\)恰有\(2\)个整数解，求实数\(a\)的取值范围.
 
 

参考答案

1.\(C\)
2.\(a>1\)时，不等式的解集是\(R\)，
\(a=1\)时，不等式的解集是\(\{x|x≠-1\}\)，
\(a<1\)时，不等式的解集是\(\{x \mid x>-1+\sqrt{1-a} \text { 或 } x<-1-\sqrt{1-a}\}\)．
3.\(a>4\)或\(a<-4\)时，不等式的解集为\(\left\{x \mid x<\dfrac{-a-\sqrt{a^{2}-16}}{4} \text { 或 } x>\dfrac{-a+\sqrt{a^{2}-16}}{4}\right\}\)
\(a＝±4\)时，不等式的解集为\(\left\{x \mid x \neq-\dfrac{a}{4}\right\}\)；
\(-4<a<4\)时，不等式的解集为\(R\)．
4. 当\(a<0\)时，解集是\(\left(-1,-\dfrac{1}{a}\right)\)；
当\(a=0\)时，解集是\((-1 ,+∞)\)；
当\(0<a≤1\)时，解集是\(\left(-\infty,-\dfrac{1}{a}\right) \cup(-1,+\infty)\)；
当\(a>1\)时，解集是\((-\infty,-1) \cup\left(-\dfrac{1}{a},+\infty\right)\)．
5.\(\left(-\dfrac{3}{2},-\dfrac{4}{3}\right] \cup\left[\dfrac{4}{3}, \dfrac{3}{2}\right)\)