欢 迎 到 学 科 网 下 载 资 料 学 习 欢 迎 到 学 科 网 下 载 资 料 学 习 https://www.zxxk.com/docpack/2783085.html )跟 贵 哥 学 数 学 , s o e a s y ! 跟 贵 哥 学 数 学 , s o e a s y !
必修第一册同步拔高练习,难度 2 颗星!
模块导图
集合的含义与表示
知识剖析
1 元素与集合的概念
2 集合的元素特征 确定性 :给定一个集合,那么任何一个元素在不在这个集合中就确定了.E g E g 互异性 :一个集合中的元素是互不相同的,即集合中的元素是不重复出现的.E g E g A = { 1 , 2 , a } A = { 1 , 2 , a } ,就意味 a ≠ 1 a ≠ 1 且 a ≠ 2 a ≠ 2 .无序性 :集合中的元素无顺序,可以任意排列、调换.E g E g { 1 , 2 , 3 } = { 2 , 3 , 1 } { 1 , 2 , 3 } = { 2 , 3 , 1 }
3 元素与集合的关系 a a 是集合 A A 的元素,则称 a a 属于集合 A A ,记作 a ∈ A a ∈ A ; a a 不是集合 A A 的元素,则称 a a 不属于集合 A A ,记作 a ∉ A a ∉ A .E g E g ∉ { ∉ { 平行四边形 } } ,0 ∈ N 0 ∈ N 0 ∉ { 1 , 2 , 3 , 4 } 0 ∉ { 1 , 2 , 3 , 4 } 脑 筋 急 转 弯 脑 筋 急 转 弯 答案: 如果上帝万能,他能否创造一块他举不起来的石头么?(这跟集合有什么关系呢?)
4 常用数集 N N ;正整数集,记作 N ∗ N ∗ 或 N + N + ;整数集,记作 Z Z ; Q Q ;实数集,记作 R R .
5 集合的分类 ∅ ∅ .E g E g { x ∣ x = 2 n + 1 , n ∈ Z } { x ∣ x = 2 n + 1 , n ∈ Z } 属于无限集,{ x ∈ R ∣ x 2 + 1 = 0 } = ∅ { x ∈ R ∣ x 2 + 1 = 0 } = ∅
6 集合的表示方法 ①列举法 ②描述法 { x ∈ A ∣ p ( x ) } { x ∈ A ∣ p ( x ) } ( 1 ) ( 1 ) ( 2 ) ( 2 ) E g E g ( 1 ) A = { x | x 2 − x − 2 = 0 } ( 1 ) A = { x | x 2 − x − 2 = 0 } x 2 − x − 2 = 0 x 2 − x − 2 = 0 的解,即 A = { − 1 , 2 } A = { − 1 , 2 } ;( 2 ) B = { x | x 2 − x − 2 < 0 } ( 2 ) B = { x | x 2 − x − 2 < 0 } x 2 − x − 2 < 0 x 2 − x − 2 < 0 的解集,即 B = { x | − 1 < x < 2 } B = { x | − 1 < x < 2 } ;( 3 ) C = { x | y = x 2 − x − 2 } ( 3 ) C = { x | y = x 2 − x − 2 } y = x 2 − x − 2 y = x 2 − x − 2 的定义域,即 C = R C = R ;( 4 ) D = { y | y = x 2 − x − 2 } ( 4 ) D = { y | y = x 2 − x − 2 } y = x 2 − x − 2 y = x 2 − x − 2 的值域,即 D = { y | y > 9 4 } D = { y | y > 9 4 } ;( 5 ) E = { ( x , y ) | y = x 2 − x − 2 } ( 5 ) E = { ( x , y ) | y = x 2 − x − 2 } y = x 2 − x − 2 y = x 2 − x − 2 的图像,它是个点集.
经典例题
【典题 1】 { 1 , 2 , 3 , 4 , 5 } { 1 , 2 , 3 , 4 , 5 } 和 { 5 , 4 , 3 , 2 , 1 } { 5 , 4 , 3 , 2 , 1 } 表示同一个集合;1 , 0.5 , 1 2 , 3 2 , 6 4 , √ 1 4 1 , 0.5 , 1 2 , 3 2 , 6 4 , 1 4 【解析】 A , B A , B D D 0.5 , 1 2 , √ 1 4 0.5 , 1 2 , 1 4 相等,3 2 , 6 4 3 2 , 6 4 3 3 个元素;集合具有无序性,所以是正确的; C C .【点拨】
【典题 2】 A = { 2 , 1 − a , a 2 − a + 2 } A = { 2 , 1 − a , a 2 − a + 2 } ,若 4 ∈ A 4 ∈ A ,则 a = a = – ––– – _ 【解析】 ∵ 4 ∈ A ∵ 4 ∈ A ∴ 1 − a = 4 ∴ 1 − a = 4 a 2 − a + 2 = 4 a 2 − a + 2 = 4 , 1 − a = 4 1 − a = 4 ,则 a = − 3 a = − 3 , a 2 − a + 2 = 14 a 2 − a + 2 = 14 ,∴ A = { 2 , 4 , 14 } ∴ A = { 2 , 4 , 14 } a 2 − a + 2 = 4 a 2 − a + 2 = 4 ,则 a = 2 a = 2 或 a = − 1 a = − 1 a = 2 a = 2 A = { 2 , − 1 , 4 } A = { 2 , − 1 , 4 } a = − 1 a = − 1 A = { 2 , 2 , 4 } A = { 2 , 2 , 4 } a ≠ − 1 a ≠ − 1 . a = 2 a = 2 或 a = − 3 a = − 3 .【点拨】 a = − 1 a = − 1 时,A = { 2 , 2 , 4 } A = { 2 , 2 , 4 }
【典题 3】 A = { 6 x − 2 ∈ Z ∣ x ∈ N } = A = { 6 x − 2 ∈ Z ∣ x ∈ N } = – ––– – _ 【解析】 x ∈ N x ∈ N ,且 6 x − 2 ∈ Z 6 x − 2 ∈ Z 可得:x = 0 x = 0 6 x − 2 = − 3 6 x − 2 = − 3 x = 1 x = 1 6 x − 2 = − 6 6 x − 2 = − 6 x = 3 x = 3 6 x − 2 = 6 6 x − 2 = 6 x = 4 x = 4 6 x − 2 = 3 6 x − 2 = 3 x = 5 x = 5 6 x − 2 = 2 6 x − 2 = 2 x = 8 x = 8 6 x − 2 = 1 6 x − 2 = 1 A = { − 3 , − 6 , 6 , 3 , 2 , 1 } A = { − 3 , − 6 , 6 , 3 , 2 , 1 } .【点拨】 6 x − 2 6 x − 2 x x
【典题 4】 A = { x ∣ a x 2 + 2 x + 1 = 0 , a ∈ R } A = { x ∣ a x 2 + 2 x + 1 = 0 , a ∈ R } 至多有一个元素,则 a a 的取值范围是 – ––– – _ .【解析】 A = { x ∣ a x 2 + 2 x + 1 = 0 , a ∈ R } A = { x ∣ a x 2 + 2 x + 1 = 0 , a ∈ R } 至多有一个元素, a = 0 a = 0 或 { a ≠ 0 △ = 4 − 4 a ≤ 0 { a ≠ 0 △ = 4 − 4 a ≤ 0 , a = 0 a = 0 或 a ≥ 1 a ≥ 1 . a a 的取值范围是 { a ∣ a = 0 或 a ≥ 1 } { a ∣ a = 0 或 a ≥ 1 } .【点拨】 0 0 ,先确认函数类型.
巩固练习
1 (★★) 设集合 M = { x ∣ x = 3 k , k ∈ Z } M = { x ∣ x = 3 k , k ∈ Z } ,P = { x ∣ x = 3 k + 1 , k ∈ Z } P = { x ∣ x = 3 k + 1 , k ∈ Z } Q = { x ∣ x = 3 k − 1 , k ∈ Z } Q = { x ∣ x = 3 k − 1 , k ∈ Z } a ∈ M , b ∈ P , c ∈ Q a ∈ M , b ∈ P , c ∈ Q ,则 a + b − c ∈ a + b − c ∈ ( )M M P P Q Q M U P M U P (★★) 若集合 A = { x ∣ k x 2 + 4 x + 4 = 0 , x ∈ R } A = { x ∣ k x 2 + 4 x + 4 = 0 , x ∈ R } 中只有一个元素,则实数 k k 的值为 – ––– – _ .(★★) 用列举法表示集合 { m ∣ m − 2 3 ∈ N , m ∈ N , m ≤ 10 } = { m ∣ m − 2 3 ∈ N , m ∈ N , m ≤ 10 } = – ––– – _
答案
1.A A 0 或 1 0 或 1 { 2 , 5 , 8 } { 2 , 5 , 8 }
集合间的关系
知识剖析
1 子集 ①概念 A , B A , B ,如果集合 A A 的任何一个元素都是集合的元素,我们说这两个集合有包含关系,称集合 A A 是集合 B B 的子集.A ⊆ B A ⊆ B B ⊇ A B ⊇ A ),读作:A A B B ,或 B B 包含 A A . A A 不包含于集合 B B 时,记作 (A ⊈ B A ⊈ B B ⊉ A B ⊉ A ).
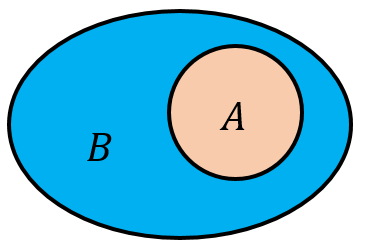
②V e n n V e n n
2 真子集 A ⊆ B A ⊆ B ,但存在元素 x ∈ B x ∈ B 且 x ∉ A x ∉ A ,则称集合 A A 是集合 B B 的真子集.A ⊂ B A ⊂ B B ⊃ A B ⊃ A )A A B B (或 B B 真包含)类 比 类 比 ⊆ ⊆ ⊂ ⊂ 的关系就好比 ≤ ≤ 与 < < 的关系,“≤ ≤ ⊆ ⊆ E g E g 3 ≤ 3 3 ≤ 3 3 < 3 3 < 3 错的,若 a < b a < b ,则 a ≤ b a ≤ b 也成立;A ⊆ A A ⊆ A A ⊂ A A ⊂ A 错的,若 A ⊂ B A ⊂ B ,则 A ⊆ B A ⊆ B 也成立. 3 集合相等 A A 是集合 B B 的子集,且集合 B B 是集合 A A 的子集,则集合 A A 与集合 B B 相等. A ⊆ B A ⊆ B 且 B ⊆ A B ⊆ A ⇔ A = B ⇔ A = B
4 几个结论 ∅ ⊆ A ∅ ⊆ A A , B , C A , B , C ,如果 A ⊆ B A ⊆ B 且 B ⊆ C B ⊆ C ,那么 A ⊆ C A ⊆ C ; n n 个元素,则子集的个数为 2 n 2 n ,真子集的个数为 2 n − 1 2 n − 1 .
经典例题
【典题 1】 A = { x ∈ N ∣ 0 < x < 4 } A = { x ∈ N ∣ 0 < x < 4 } 的子集个数.【解析】 A = { x ∈ N ∣ 0 < x < 4 } = { 1 , 2 , 3 } A = { x ∈ N ∣ 0 < x < 4 } = { 1 , 2 , 3 } ,( 先 化 简 集 合 ) ( 先 化 简 集 合 ) ∅ , { 1 } , { 2 } , { 3 } , { 1 , 2 } ∅ , { 1 } , { 2 } , { 3 } , { 1 , 2 } ,{ 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 } { 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 } 2 3 = 8 2 3 = 8 个.【点拨】 n n 个元素,则子集的个数为 2 n 2 n ,真子集的个数为 2 n − 1 2 n − 1 .
【典题 2】 A = { x ∣ x 2 − 3 x + 2 = 0 } A = { x ∣ x 2 − 3 x + 2 = 0 } ,B = { x ∣ x 2 + 2 ( a + 1 ) x + a 2 − 5 = 0 } B = { x ∣ x 2 + 2 ( a + 1 ) x + a 2 − 5 = 0 } B ⊆ A B ⊆ A ,则 a a 的取值范围 – ––– – _ .【解析】 A = { 1 , 2 } A = { 1 , 2 } ,因为 B ⊆ A B ⊆ A ,则 B = ∅ B = ∅ 或 { 1 } { 1 } 或 { 2 } { 2 } 或 { 1 , 2 } { 1 , 2 } , B = ∅ B = ∅ ,所以 Δ = 4 ( a + 1 ) 2 − 4 ( a 2 − 5 ) = 8 a + 24 < 0 Δ = 4 ( a + 1 ) 2 − 4 ( a 2 − 5 ) = 8 a + 24 < 0 ,解得 a < − 3 a < − 3 ; B = { 1 } B = { 1 } ,则 { △ = 8 a + 24 = 0 1 + 2 ( a + 1 ) + a 2 − 5 = 0 { △ = 8 a + 24 = 0 1 + 2 ( a + 1 ) + a 2 − 5 = 0 ,无解;( 不 要 漏 了 Δ = 0 ) ( 不 要 漏 了 Δ = 0 ) B = { 2 } B = { 2 } ,则 { Δ = 8 a + 24 = 0 4 + 4 ( a + 1 ) + a 2 − 5 = 0 { Δ = 8 a + 24 = 0 4 + 4 ( a + 1 ) + a 2 − 5 = 0 ,解得 a = 3 a = 3 ; B = { 1 , 2 } B = { 1 , 2 } ,则无解.【点拨】 B ⊆ A B ⊆ A ,注意不能忽略了 B = ∅ B = ∅ 这种情况.
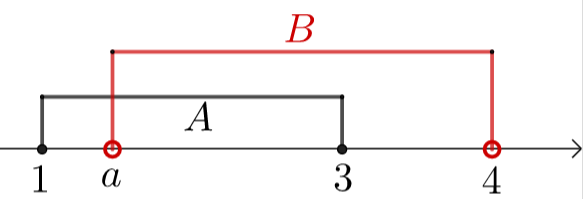
【典题 3】 A = { x ∣ x 2 − 5 x + 4 ≤ 0 } A = { x ∣ x 2 − 5 x + 4 ≤ 0 } ,B = { x ∣ x 2 − 2 a x + a + 2 ≤ 0 } B = { x ∣ x 2 − 2 a x + a + 2 ≤ 0 } B ⊆ A B ⊆ A , a a 的取值范围为 – ––– – _ 【解析】 A = { x ∣ x 2 − 5 x + 4 ≤ 0 } = { x ∣ 1 ≤ x ≤ 4 } A = { x ∣ x 2 − 5 x + 4 ≤ 0 } = { x ∣ 1 ≤ x ≤ 4 } ,B = { x ∣ x 2 − 2 a x + a + 2 ≤ 0 } B = { x ∣ x 2 − 2 a x + a + 2 ≤ 0 } ∵ B ⊆ A ∵ B ⊆ A ( 分 B = ∅ 或 B ≠ ∅ 两 种 情 况 讨 论 ) ( 分 B = ∅ 或 B ≠ ∅ 两 种 情 况 讨 论 ) ∴ ( i ) ∴ ( i ) B = ∅ B = ∅ 时,x 2 − 2 a x + a + 2 ≤ 0 x 2 − 2 a x + a + 2 ≤ 0 Δ < 0 ⇒ 4 a 2 − 4 ( a + 2 ) < 0 Δ < 0 ⇒ 4 a 2 − 4 ( a + 2 ) < 0 ,解得 − 1 < a < 2 − 1 < a < 2 .( i i ) ( i i ) B ≠ ∅ B ≠ ∅ 时,要使 B ⊆ A B ⊆ A 成立, f ( x ) = x 2 − 2 a x + a + 2 f ( x ) = x 2 − 2 a x + a + 2 , ⎧ ⎪
⎪
⎪
⎪
⎪
⎪ ⎨ ⎪
⎪
⎪
⎪
⎪
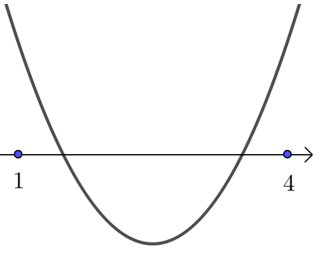
⎪ ⎩ Δ ≥ 0 1 < − − 2 a 2 < 4 f ( 1 ) ≥ 0 f ( 4 ) ≥ 0 { Δ ≥ 0 1 < − − 2 a 2 < 4 f ( 1 ) ≥ 0 f ( 4 ) ≥ 0 ,解得 2 ≤ a ≤ 18 7 2 ≤ a ≤ 18 7 ,如 图 所 示 如 图 所 示
综上可得 − 1 < a ≤ 18 7 − 1 < a ≤ 18 7 .【点拨】
巩固练习
1(★★) A = { x ∣ x = k + 1 6 , k ∈ N } A = { x ∣ x = k + 1 6 , k ∈ N } ,B = { x ∣ x = m 2 − 1 3 , m ∈ N } B = { x ∣ x = m 2 − 1 3 , m ∈ N } C = { x ∣ x = n 2 + 1 6 , n ∈ N } C = { x ∣ x = n 2 + 1 6 , n ∈ N } A A 、B B C C A ⫋ C ⫋ B A ⫋ C ⫋ B C ⫋ A ⫋ B C ⫋ A ⫋ B A ⫋ B = C A ⫋ B = C A ⫋ B ⫋ C A ⫋ B ⫋ C
2(★★) A = { x | x > 1 } A = { x | x > 1 } ,B = { x ∣ a x > 1 } B = { x ∣ a x > 1 } B ⊆ A B ⊆ A ,则实数 a a 的取值范围 – ––– – _ .(★★★) A = { x ∣ 1 ≤ x ≤ 2 } A = { x ∣ 1 ≤ x ≤ 2 } ,B = { x ∣ x 2 − a x + 4 ≥ 0 } B = { x ∣ x 2 − a x + 4 ≥ 0 } A ⊆ B A ⊆ B ,则实数 a a 的取值范围是 – ––– – _ .
参考答案
1.A A [ 0 , 1 ] [ 0 , 1 ] a < 4. a < 4.
集合的基本运算
知识剖析
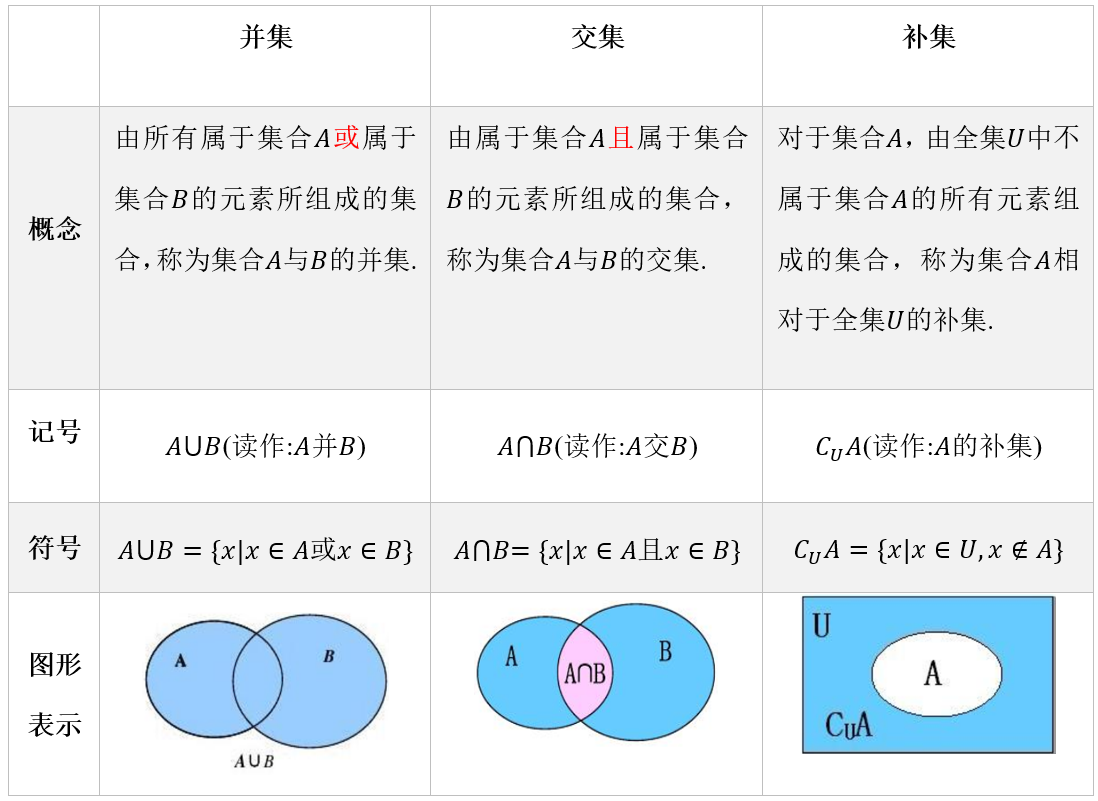
1 并集、交集、补集
2 结论 A ∩ B = A A ∩ B = A ,则 A ⊆ B A ⊆ B ; A ∪ B = A A ∪ B = A ,则 B ⊆ A B ⊆ A .
3 运算律 A ∪ B = B ∪ A A ∪ B = B ∪ A ,A ∩ B = B ∩ A A ∩ B = B ∩ A ( A ∪ B ) ∪ C = A ∪ ( B ∪ C ) ( A ∪ B ) ∪ C = A ∪ ( B ∪ C ) ,( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) ( A ∩ B ) ∪ C = ( A ∩ C ) ∪ ( B ∩ C ) ( A ∩ B ) ∪ C = ( A ∩ C ) ∪ ( B ∩ C ) ,( A ∪ B ) ∩ C = ( A ∩ C ) ∪ ( B ∩ C ) ( A ∪ B ) ∩ C = ( A ∩ C ) ∪ ( B ∩ C ) C U ( A ∪ B ) = ( C U A ) ∩ ( C U B ) C U ( A ∪ B ) = ( C U A ) ∩ ( C U B ) , C U ( A ∩ B ) = ( C U A ) ∪ ( C U B ) C U ( A ∩ B ) = ( C U A ) ∪ ( C U B )
经典例题
【典题 1】 U = { x ∈ Z ∣ − 3 < x < 8 } U = { x ∈ Z ∣ − 3 < x < 8 } ,C U M = { − 2 , 1 , 3 , 4 , 7 } C U M = { − 2 , 1 , 3 , 4 , 7 } N = { − 2 , − 1 , 2 , 4 , 5 , 7 } N = { − 2 , − 1 , 2 , 4 , 5 , 7 } M ∩ N M ∩ N 的元素个数为 – ––– – _ .【解析】 U = { − 2 , − 1 , 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 } U = { − 2 , − 1 , 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 } M = { − 1 , 0 , 2 , 5 , 6 } M = { − 1 , 0 , 2 , 5 , 6 } ,∴ M ∩ N = { − 1 , 2 , 5 } ∴ M ∩ N = { − 1 , 2 , 5 } ∴ M ∩ N ∴ M ∩ N 3 3 .
【典题 2】 U = R U = R , 集合 A = { x | x 2 − 3 x − 4 < 0 } A = { x | x 2 − 3 x − 4 < 0 } ,B = { x | x − 1 ≤ 0 } B = { x | x − 1 ≤ 0 } A ∩ C U B = A ∩ C U B = – ––– – _ 【解析】 ∵ A = { x ∣ − 1 < x < 4 } ∵ A = { x ∣ − 1 < x < 4 } B = { x ∣ x ≤ 1 } B = { x ∣ x ≤ 1 } U = R U = R ∴ C U B = { x ∣ x > 1 } ∴ C U B = { x ∣ x > 1 } , ∴ A ∩ C U B = { x ∣ 1 < x < 4 } ∴ A ∩ C U B = { x ∣ 1 < x < 4 } 【点拨】
【典题 3】 A = { x ∣ x 2 + 8 x = 0 } A = { x ∣ x 2 + 8 x = 0 } ,B = { x ∣ x 2 + 2 ( a + 2 ) x + a 2 − 4 = 0 } B = { x ∣ x 2 + 2 ( a + 2 ) x + a 2 − 4 = 0 } a ∈ R a ∈ R , A ∪ B = A A ∪ B = A ,求实数 a a 的取值范围.【解析】 ∵ x 2 + 8 x = 0 ∵ x 2 + 8 x = 0 ∴ x ( x + 8 ) = 0 ∴ x ( x + 8 ) = 0 x = 0 x = 0 或 x = − 8 x = − 8 ,∴ A = { 0 , − 8 } ∴ A = { 0 , − 8 } ∵ A ∪ B = A ∵ A ∪ B = A ∴ B ⊆ A ∴ B ⊆ A ( 利 用 v e n n 图 理 解 下 这 个 结 论 ) ( 利 用 v e n n 图 理 解 下 这 个 结 论 ) ∴ B ∴ B ∅ , { 0 } , { − 8 } , { 0 , − 8 } ∅ , { 0 } , { − 8 } , { 0 , − 8 } . x 2 + 2 ( a + 2 ) x + a 2 − 4 = 0 ( ⊗ ) x 2 + 2 ( a + 2 ) x + a 2 − 4 = 0 ( ⊗ ) 的 Δ = 4 ( a + 2 ) 2 − 4 ( a 2 − 4 ) = 16 ( a + 2 ) Δ = 4 ( a + 2 ) 2 − 4 ( a 2 − 4 ) = 16 ( a + 2 ) . Δ = 0 Δ = 0 ,即 a = − 2 a = − 2 时,此时 B = { 0 } B = { 0 } ,适合题意. △ < 0 △ < 0 ,即 a < − 2 a < − 2 时,得 B = ∅ B = ∅ ,适合题意. △ > 0 △ > 0 ,即 a > − 2 a > − 2 时,方程 (⊗) 由两个不等根,若为 0 , − 8 0 , − 8 , { − 8 + 0 = − 2 ( a + 2 ) − 8 × 0 = a 2 − 4 { − 8 + 0 = − 2 ( a + 2 ) − 8 × 0 = a 2 − 4 ,解得 a = 2 a = 2 . ( 韦 达 定 理 ) ( 韦 达 定 理 ) a a 的取值范围是 { a | a = 2 或 a ≤ − 2 } { a | a = 2 或 a ≤ − 2 } .【点拨】 B ⊆ A B ⊆ A B = ∅ B = ∅ 的情况.
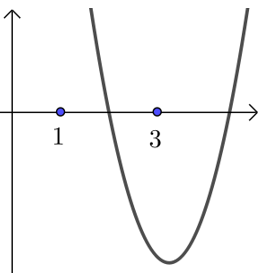
【典题 4】 A = { x | x 2 − 4 x + 3 ≤ 0 } A = { x | x 2 − 4 x + 3 ≤ 0 } ,B = { x | x 2 + m x + n < 0 } B = { x | x 2 + m x + n < 0 } A ∩ B ≠ ∅ A ∩ B ≠ ∅ ,A ∪ B = { x ∣ 1 ≤ x < 4 } A ∪ B = { x ∣ 1 ≤ x < 4 } m m 的取值范围.【解析】 A = { x | 1 ≤ x ≤ 3 } A = { x | 1 ≤ x ≤ 3 } , ∵ A ∩ B ≠ ∅ ∵ A ∩ B ≠ ∅ A ∪ B = { x ∣ 1 ≤ x < 4 } A ∪ B = { x ∣ 1 ≤ x < 4 } 此 时 画 数 轴 分 析 下 , 会 清 晰 很 多 此 时 画 数 轴 分 析 下 , 会 清 晰 很 多 则 易 知 a 、 4 是 方 程 x 2 + m x + n = 0 的 根 , 且 1 ≤ a < 3 则 易 知 a 、 4 是 方 程 x 2 + m x + n = 0 的 根 , 且 1 ≤ a < 3 ∴ x = 4 ∴ x = 4 x 2 + m x + n = 0 x 2 + m x + n = 0 的一个根, 16 + 4 m + n = 0 16 + 4 m + n = 0 , 并且另一个根在 [ 1 , 3 ) [ 1 , 3 ) 上,此 时 还 是 试 试 画 出 满 足 条 件 的 f ( x ) = x 2 + m x + n 函 数 图 象 , 体 会 下 数 形 结 合 的 威 力 此 时 还 是 试 试 画 出 满 足 条 件 的 f ( x ) = x 2 + m x + n 函 数 图 象 , 体 会 下 数 形 结 合 的 威 力 ∴ ∴ f ( x ) = x 2 + m x + n f ( x ) = x 2 + m x + n , 则 f ( 1 ) f ( 3 ) ≤ 0 f ( 1 ) f ( 3 ) ≤ 0 , 其中 f ( 3 ) ≠ 0 f ( 3 ) ≠ 0 ,∴ ⎧ ⎪ ⎨ ⎪ ⎩ 16 + 4 m + n = 0 ( 1 + m + n ) ( 9 + 3 m + n ) ≤ 0 9 + 3 m + n ≠ 0 ∴ { 16 + 4 m + n = 0 ( 1 + m + n ) ( 9 + 3 m + n ) ≤ 0 9 + 3 m + n ≠ 0 − 7 < m ≤ − 5 − 7 < m ≤ − 5 .
【点拨】
巩固练习
1(★) P = { x | x + 2 ≥ x 2 } P = { x | x + 2 ≥ x 2 } ,Q = { x ∈ N | | x | ≤ 3 } Q = { x ∈ N | | x | ≤ 3 } P ∩ Q = P ∩ Q = – ––– – _
2(★) A = { x | x 2 − x − 2 < 0 } A = { x | x 2 − x − 2 < 0 } ,B = { x | a − 2 < x < a } B = { x | a − 2 < x < a } A ∩ B = { x ∣ − 1 < x < 0 } A ∩ B = { x ∣ − 1 < x < 0 } ,则 A ∪ B = A ∪ B = – ––– – _
3(★★) A = { x ∣ x 2 − 5 x + 6 = 0 } A = { x ∣ x 2 − 5 x + 6 = 0 } ,B = { x │ m x + 1 = 0 } B = { x │ m x + 1 = 0 } A ∪ B = A A ∪ B = A , 则实数 m m 的取值集合为 – ––– – _ .
挑战学霸 1 已知集合 A = { x ∣ x = m + n √ 3 A = { x ∣ x = m + n 3 , 且 m 2 − 3 n 2 = 1 , m , n ∈ Z } , 且 m 2 − 3 n 2 = 1 , m , n ∈ Z } x ∈ A x ∈ A ,则 x + 1 x x + 1 x 是偶数; a ∈ A a ∈ A ,且 1 < a < 4 1 < a < 4 ,求实数 a a 的值; c ∈ A c ∈ A ,求证:c 2 + √ 3 ∈ A c 2 + 3 ∈ A 2 + √ 3 < c ≤ ( 2 + √ 3 ) 2 2 + 3 < c ≤ ( 2 + 3 ) 2 的 c c 的值.
2 (清华大学自招真题) A = { a 1 , a 2 , … , a n } A = { a 1 , a 2 , … , a n } ,任取 1 ≤ i < j < k ≤ n 1 ≤ i < j < k ≤ n ,a i + a j ∈ A a i + a j ∈ A a j + a k ∈ A , a i + a k ∈ A a j + a k ∈ A , a i + a k ∈ A n n 的最大值为 – ––– – _ .
参考答案
1.0 , 1 , 2 0 , 1 , 2 ( − 2 , 2 ) ( − 2 , 2 ) { − 1 2 , 1 3 , 0 } { − 1 2 , 1 3 , 0 }
挑战学霸
解 (1) 因为 x ∈ A x ∈ A , 不妨设 x = m + n √ 3 x = m + n 3 , x + 1 x = ( m + n √ 3 ) + 1 m + √ 3 n x + 1 x = ( m + n 3 ) + 1 m + 3 n = m + √ 3 n + m − √ 3 n m 2 − 3 n 2 = m + 3 n + m − 3 n m 2 − 3 n 2 m 2 − 3 n 2 = 1 m 2 − 3 n 2 = 1 可得 x + 1 x = 2 m x + 1 x = 2 m m ∈ Z m ∈ Z , 所以 x + 1 x x + 1 x 为偶数. x ∈ A x ∈ A , 不妨设 x = m + n √ 3 x = m + n 3 , 1 < a < 4 1 < a < 4 可得 1 4 < 1 a < 1 1 4 < 1 a < 1 , a + 1 a = 2 m a + 1 a = 2 m , 5 4 < 2 m < 5 5 4 < 2 m < 5 ,即 5 8 < m < 5 2 5 8 < m < 5 2 m 2 − 3 n 2 = 1 m 2 − 3 n 2 = 1 ,m , n ∈ Z m , n ∈ Z m = 1 m = 1 或 2 2 m = 1 m = 1 时 n = 0 n = 0 不符合, m = 2 m = 2 时,n = 1 n = 1 a = 2 + √ 3 a = 2 + 3 , c ∈ A c ∈ A , 则设 c = m + n √ 3 c = m + n 3 , c 2 + √ 3 = m + √ 3 n 2 + √ 3 c 2 + 3 = m + 3 n 2 + 3 = ( m + √ 3 n ) ( 2 − √ 3 ) 4 − 3 = ( 2 m − 3 n ) + √ 3 ( 2 n − m ) = ( m + 3 n ) ( 2 − 3 ) 4 − 3 = ( 2 m − 3 n ) + 3 ( 2 n − m ) 2 m − 3 n 、 2 n − m ∈ Z 2 m − 3 n 、 2 n − m ∈ Z , ( 2 m + 3 n ) 2 − 3 ( 2 n − m ) 2 = 1 ( 2 m + 3 n ) 2 − 3 ( 2 n − m ) 2 = 1 符合集合 A A 定义, 2 + √ 3 < c ≤ ( 2 + √ 3 ) 2 2 + 3 < c ≤ ( 2 + 3 ) 2 1 < c 2 + √ 3 ≤ 2 + √ 3 1 < c 2 + 3 ≤ 2 + 3 c 2 + √ 3 = 2 + √ 3 c 2 + 3 = 2 + 3 , c = ( 2 + √ 3 ) 2 = 7 + 4 √ 3 c = ( 2 + 3 ) 2 = 7 + 4 3 .
解 不妨假设 a 1 > a 2 > ⋯ > a n a 1 > a 2 > ⋯ > a n ,若集合 A A 中的正数个数大于等于 4 4 ,由于 a 2 + a 3 a 2 + a 3 和 a 2 + a 4 a 2 + a 4 均大于 a 2 a 2 ,于是有 a 2 + a 3 = a 2 + a 4 = a 1 a 2 + a 3 = a 2 + a 4 = a 1 ,从而 a 3 = a 4 a 3 = a 4 ,矛盾! A A 中至多有 3 3 个正数, A A 中最多有 3 3 个负数, A = { − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 } A = { − 3 , − 2 , − 1 , 0 , 1 , 2 , 3 } ,满足题意,所以 n n 的最大值为 7 7 .
 )
)
 )
) )
)



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通