1.4.1 空间向量的应用---线面位置关系的证明
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第一册同步拔高,难度3颗星!
知识剖析
1 直线的方向向量和平面的法向量
(1)直线的方向向量
若\(A\)、\(B\)是直线\(l\)上的任意两点,则\(\overrightarrow{A B}\)为直线\(l\)的一个方向向量;与\(\overrightarrow{A B}\)平行的任意非零向量也是直线\(l\)的方向向量.
(2)平面的法向量
若向量\(\vec{n}\)所在直线垂直于平面\(α\),则称这个向量垂直于平面\(α\),记作\(\vec{n} \perp α\),向量\(\vec{n}\)叫做平面\(α\)的法向量.
(3)平面的法向量的求法(待定系数法)
① 建立适当的坐标系;
② 设平面\(α\)的法向量为\(\vec{n}=(x, y, z)\);
③ 求出平面内两个不共线向量的坐标\(\vec{a}=\left(a_{1}, a_{2}, a_{3}\right)\),\(\vec{b}=\left(b_{1}, b_{2}, b_{3}\right)\);
④ 根据法向量定义建立方程组\(\left\{\begin{array}{l}
\vec{n} \cdot \vec{a}=0 \\
\vec{n} \cdot \vec{b}=0
\end{array}\right.\)
⑤ 解方程组,取其中一组解,即得平面\(α\)的法向量.
2 判定空间的平行关系
(1)线线平行
设直线\(l_1\),\(l_2\)的方向向量分别是\(\vec{a}\),\(\vec{b}\),则要证明\(l_1 || l_2\),只需证明\(\vec{a} \| \vec{b}\),即\(\vec{a}=k \vec{b}(k \in R)\).
(2)线面平行
设直线\(l\)的方向向量是\(\vec{a}\),平面\(α\)的法向量是\(\vec{n}\),则要证明\(l||α\),
只需证明\(\vec{a} \perp \vec{n}\),即\(\vec{a} \cdot \vec{n}=0\).
(3)面面平行
若平面\(α\)的法向量为\(\overrightarrow{n_{1}}\),平面\(β\)的法向量为\(\overline{n_{2}}\),要证\(α||β\),只需证\(\overrightarrow{n_{1}} \| \overrightarrow{n_{2}}\),即证\(\overrightarrow{n_{1}}=\lambda \overrightarrow{n_{2}}\).
3 判定空间的垂直关系
(1)线线垂直
设直线\(l_1\),\(l_2\)的方向向量分别是\(\vec{a}\),\(\vec{b}\),则要证明\(l_1⊥ l_2\),只需证明\(\vec{a} \perp \vec{b}\),即\(\vec{a} \cdot \vec{b}=0\).
(2)线面垂直
①(法一)设直线\(l\)的方向向量是\(\vec{a}\),平面\(α\)的法向量是\(\vec{n}\),则要证明\(l⊥α\),只需证明\(\vec{a} \| \vec{n}\),即\(\vec{a}=\lambda \vec{n}\).
②(法二)设直线\(l\)的方向向量是\(\vec{a}\),平面\(α\)内的两个相交向量分别为\(\vec{m}\),\(\vec{n}\),
若\(\left\{\begin{array}{l}
\vec{a} \cdot \vec{m}=0 \\
\vec{a} \cdot \vec{n}=0
\end{array}\right.\),则\(l⊥α\).
(3)面面垂直
若平面\(α\)的法向量为\(\overrightarrow{n_{1}}\),平面\(β\)的法向量为\(\overrightarrow{n_{2}}\),要证\(α⊥β\),
只需证\(\overrightarrow{n_{1}} \perp \overrightarrow{n_{2}}\),即证\(\overrightarrow{n_{1}} \cdot \overrightarrow{n_{2}}=0\).
经典例题
【典题1】若平面\(α\)与\(β\)的法向量分别是\(\vec{a}=(2,4,-3)\),\(\vec{b}=(-1,2,2)\),则平面\(α\)与\(β\)的位置关系是( )
A.平行 \(\qquad \qquad \qquad \qquad\) B.垂直 \(\qquad \qquad \qquad \qquad\) C.相交但不垂直 \(\qquad \qquad \qquad \qquad\) D.无法确定
【解析】\(\because \vec{a} \cdot \vec{b}=(2,4,-3)(-1,2,2)=-2+8-6=0\)
\(\therefore \vec{a} \perp \vec{b}\),
\(∴\)平面\(α\)与平面\(β\)垂直
故选:\(B\).
【典题2】如图\(1\)所示,在边长为\(12\)的正方形\(A A^{\prime} A_{1}^{\prime} A_{1}\)中,点\(B\),\(C\)在线段\(AA'\)上,且\(AB=3\),\(BC=4\),作\(BB_1∥AA_1\),分别交\(A_{1} A_{1}^{\prime}\)、\(A A_{1}^{\prime}\)于点\(B_1\)、\(P\),作\(CC_1∥AA_1\),分别交\(A_{1} A_{1}^{\prime}\)、\(A A_{1}^{\prime}\)于点\(C_1\)、\(Q\),将该正方形沿\(BB_1\)、\(CC_1\)折叠,使得\(A^{\prime} A_{1}{ }^{\prime}\)与\(AA_1\)重合,构成如图\(2\)所示的三棱柱\(ABC-A_1 B_1 C_1\).

(1)在三棱柱\(ABC-A_1 B_1 C_1\)中,求证:\(AB⊥\)平面\(BCC_1 B_1\);
(2)试判断直线\(AQ\)是否与平面\(A_1 C_1 P\)平行,并说明理由.
【解析】(1)证明\(∵AB=3\),\(BC=4\),\(∴AC=12-3-4=5\),
从而有\(AC^2=AB^2+BC^2\),\(∴AB⊥BC\),
又\(∵AB⊥BB_1\),\(BC∩BB_1=B\),
\(∴AB⊥\)平面\(BCC_1 B_1\).
(2)直线\(AQ\)与平面\(A_1 C_1 P\)不平行.
理由如下:
以\(B\)为原点,\(BA\)为\(x\)轴,\(BC\)为\(y\)轴,\(BB_1\)为\(z\)轴,建立空间直角坐标系,

\(A(3,0,0)\),\(Q(0,4,7)\),\(A_1 (3,0,12)\),\(C_1 (0,4,12)\),\(P(0,0,3)\),
\(\overrightarrow{A Q}=(-3,4,7)\),\(\overrightarrow{P A_{1}}=(3,0,9)\),\(\overrightarrow{P C_{1}}=(0,4,9)\),
设平面\(A_1 C_1 P\)的法向量\(\vec{n}=(x, y, z)\),
则\(\left\{\begin{array}{l}
\vec{n} \cdot \overrightarrow{P A_{1}}=3 x+9 z=0 \\
\vec{n} \cdot \overrightarrow{P C_{1}}=4 y+9 z=0
\end{array}\right.\),取\(x=3\),得\(\vec{n}=\left(3, \dfrac{9}{4},-1\right)\),
\(\because \overrightarrow{A Q} \cdot \vec{n}=-9+9-7=-7 \neq 0\),
\(∴\)直线\(AQ\)与平面\(A_1 C_1 P\)不平行.
【点拨】
① 当题中出现多线段长度,注意可利用勾股定理逆定理证明线段垂直的方法;
② 第一问利用线面垂直判定定理便可证明,不需要利用向量法;
③ 第二问用高一线面平行判定定理很难做出来,此时想到向量法;思路如下,
\(AQ//\)平面\(A_{1} C_{1} P \Leftrightarrow \overrightarrow{A Q} \cdot \vec{n}=0\)(\(\vec{n}\)为平面\(A_1 C_1 P\)的法向量).
④ 利用待定系数法求平面\(A_1 C_1 P\)的法向量\(\vec{n}\).
【典题3】如图,在直三棱柱\(ABC-A_1 B_1 C_1\)中,\(A_1 B_1=A_1 C_1\),\(F\)为\(B_1 C_1\)的中点,\(D\),\(E\)分别是棱\(BC\),\(CC_1\)上的点,且\(AD⊥BC\).
(1) 求证:直线\(A_1 F∥\)平面\(ADE\);
(2) 若\(∆ABC\)是正三角形,\(E\)为\(C_1 C\)中点,能否在线段\(B_1 B\)上找一点\(N\),使得\(A_1 N∥\)平面\(ADE\)?若存在,确定该点位置;若不存在,说明理由.

【解析】(1)证明:在直三棱柱\(ABC-A_1 B_1 C_1\)中,
\(∵AB=AC,AD⊥BC\),\(∴D\)是\(BC\)的中点,
又\(∵F\)为\(B_1 C_1\)的中点\(∴DF//AA_1\)
\(∴\)四边形\(DFA_1 A\)是平行四边形,
\(∴A_1 F∥AD\),
\(∵A_1 F⊄\)平面\(ADE\),\(AD⊂\)平面\(ADE\),
\(∴A_1 F∥\)平面\(ADE\).
(2)在直线\(B_1 B\)上找一点\(N\),使得\(A_1 N∥\)平面\(ADE\),证明如下:
在直三棱柱\(ABC-A_1 B_1 C_1\)中,\(∵DF//AA_1\)
\(∴DF⊥AD\),\(DF⊥DC\)
又\(∵AD⊥BC\)\(∴DA\),\(DC\),\(DF\)两两垂直,
以\(D\)为原点,\(DA\)为\(x\)轴,\(DC\)为\(y\)轴,\(DF\)为\(z\)轴,建立空间直角坐标系,

设\(A_1 B_1=2\),\(AA_1=2t\),
\(∵N\)在线段\(B_1 B\)上,设\(BN=λBB_1\),\(0≤λ≤1\),则\(N(0,-1,2λt)\),
则\(A(\sqrt{3}, 0,0)\),\(D(0,0,0)\),\(E(0,1,t)\),\(B(0,-1,0)\),\(B_1 (0,-1,2t)\),\(A_{1}(\sqrt{3}, 0,2 t)\),
\(\overrightarrow{D A}=(\sqrt{3}, 0,0)\),\(\overrightarrow{D E}=(0,1, t)\),\(\overrightarrow{A_{1} N}=(-\sqrt{3}, \quad-1,(2 \lambda-2) t)\),
设平面\(ADE\)的法向量\(\vec{n}=(x, y, z)\),
则\(\left\{\begin{array}{l}
\vec{n} \cdot \overrightarrow{D A}=\sqrt{3} x=0 \\
\vec{n} \cdot \overrightarrow{D E}=y+t z=0
\end{array}\right.\),取\(z=1\),得\(\vec{n}=(0,-t, 1)\),
\(∵A_1 N∥\)平面\(ADE\),
\(\overrightarrow{A_{1} N} \cdot \vec{n}=0+t+(2 \lambda-2) t=0\),解得\(\lambda=\dfrac{1}{2}\),
\(∴\)在直线\(B_1 B\)上存在一点\(N\),且\(BN=\dfrac{1}{2} B B_{1}\),使得\(A_1 N∥\)平面\(ADE\).
【点拨】
① 第一问利用线面平行判定定理易证明;
② 题中线段没有给到具体值,可作假设\(A_1 B_1=2\),便于建系后确定点坐标,同时减少计算量,直棱柱的高\(AA_1\)与\(A_1 B_1\)长度没联系,所有只能设\(AA_1=2t\).
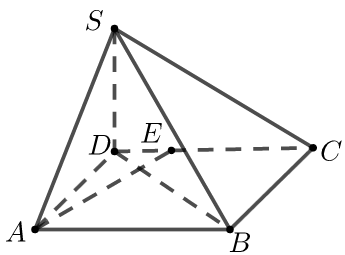
【典题4】如图,四棱锥\(S-ABCD\)中.\(ABCD\)为矩形,\(SD⊥AD\),且\(SD⊥AB\),\(AD=1\),\(AB=2\),\(S D=\sqrt{3}\).\(E\)为\(CD\)上一点,且\(CE=3DE\).
(1)求证:\(AE⊥\)平面\(SBD\);
(2)\(M\)、\(N\)分别在线段\(SB\)、\(CD\)上的点,是否存在\(M\)、\(N\),使\(MN⊥CD\)且\(MN⊥SB\),若存在,确定\(M\)、\(N\)的位置;若不存在,说明理由.
【解析】(1) \({\color{Red}{ 方法一}}\)
证明:\(∵ SD⊥AD\),且\(SD⊥AB\),\(∴SD⊥\)平面\(ABCD\).
又\(∵AD⊥CD\)
可建立如图所示的空间直角坐标系,
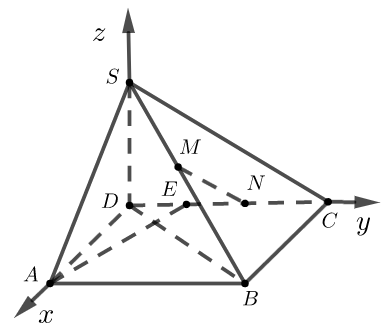
由题意可知\(D(0,0,0)\),\(E\left(0, \dfrac{1}{2}, 0\right)\),\(B(1,2,0)\),\(A(1,0,0)\),\(C(0,2,0)\),\(S(0,0, \sqrt{3})\)
\(\therefore \overrightarrow{A E}=\left(-1, \dfrac{1}{2}, 0\right)\),\(\overrightarrow{D B}(1,2,0)\),\(\overrightarrow{D S}(0,0, \sqrt{3})\)
\(\therefore \overrightarrow{A E} \cdot \overrightarrow{D B}=0\),\(\overrightarrow{A E} \cdot \overrightarrow{D S}=0\)
\(∴AE⊥DB\),\(AE⊥DS\)
又\(DB∩DS=D\)
\(∴AE⊥\)平面\(SBD\);
\({\color{Red}{ 方法二}}\)
\(∵ SD⊥AD\),且\(SD⊥AB\),\(∴SD⊥\)平面\(ABCD\)
\(∴SD⊥AE\)
如图:

\(\because \tan \angle D A E=\dfrac{D E}{A D}=\dfrac{1}{2}\),\(\tan \angle D B A=\dfrac{A D}{A B}=\dfrac{1}{2}\),
\(∴∠DAE=∠DBA\)
\(∴∠DBA+∠EAB=90°\).
\(∴AE⊥BD\);
\(∴AE⊥\)平面\(SBD\);
(2)假设存在\(MN\)满足\(MN⊥CD\)且\(MN⊥SB\).
在空间直角坐标系中,\(\overrightarrow{B S}=(-1,-2, \sqrt{3})\),
\(∵M\)在线段\(CD\)上 可设\(\overrightarrow{B M}=\lambda \overrightarrow{B S}=(-\lambda,-2 \lambda, \sqrt{3} \lambda) \quad(\lambda \in[0,1])\)
\(\because \overrightarrow{D M}=\overrightarrow{D B}+\overrightarrow{B M}=(1,2,0)+(-\lambda,-2 \lambda, \sqrt{3} \lambda)=(1-\lambda, 2-2 \lambda, \sqrt{3} \lambda)\)
\(∴M\)的坐标\((1-λ,2-2λ,√3 λ)\),
\(∵N\)在线段\(SB\)上 可设\(N(0,y,0)\),\(y∈[0,2]\)
则\(\overrightarrow{N M}=(1-\lambda, 2-2 \lambda-y, \sqrt{3} \lambda)\).
要使\(MN⊥CD\)且\(MN⊥SB\),
则\(\left\{\begin{array}{l}
\overrightarrow{N M} \cdot \overrightarrow{D C}=0 \\
\overrightarrow{N M} \cdot \overrightarrow{B S}=0
\end{array}\right.\)
可得\(\left\{\begin{array}{l}
2(2-2 \lambda-y)=0 \\
-(1-\lambda)-2(2-2 \lambda-y)+3 \lambda=0
\end{array}\right.\),
解得\(\lambda=\dfrac{1}{4} \in[0,1]\),\(y=\dfrac{3}{2} \in[0,2]\)
故存在\(MN\)使\(MN⊥CD\)且\(MN⊥SB\),其中\(M\)是线段\(SB\)靠近\(B\)的四等分点,\(N\)是线段\(CD\)靠\(近C\)的四等分点.
【点拨】
① 对于高一非向量法与向量法的取舍,若第一问非向量法较容易解答,而第二问很难则第一问用非向量法,第二问用向量法;若第一问用非向量法较难,则建议从第一问就开始利用向量法,比如该题,不用纠结第一问用向量法要建系描点浪费时间,其实不然,因为第二问大多数情况下都使用向量法的;
② 第一问方法二中利用平面几何知识点怎么垂直关系,常见技巧是勾股定理逆定理、相似三角形、三角函数等;
③ 三点共线设元问题:“\(∵M\)在线段\(CD\)上,可设\(\overrightarrow{B M}=\lambda \overrightarrow{B S}=(-\lambda,-2 \lambda, \sqrt{3} \lambda) \quad(\lambda \in[0,1])\)”中,常用向量共线的方法:\(\overrightarrow{B M}=\lambda \overrightarrow{B S}\),同时要注意变量\(λ\)的取值范围.
巩固练习
1(★)已知\(\vec{n}=(1,2,-1)\)为平面\(α\)的一个法向量,\(\vec{a}=(-2, \lambda, 1)\)为直线\(l\)的方向向量.若\(l∥α\),则\(λ=\) \(\underline{\quad \quad}\).
2(★)已知平面\(α\)的法向量是\(\vec{a}=(3 x-1,-1, x+5)\),平面\(β\)的法向量是\(\vec{b}=\left(x+1, x^{2}+3,-x\right)\),且\(α⊥β\),则实数\(x\)的值为\(\underline{\quad \quad}\).
3(★★)如图,在直三棱柱\(ABC-A_1 B_1 C_1\)中,\(AB⊥AC\),\(AB=AC=AA_1\),\(D\)为\(BC\)的中点.
(1)证明:\(A_1 B∥\)平面\(ADC_1\);
(2)证明:平面\(ADC_1⊥\)平面\(BB_1 C_1 C\).

4(★★★)如图\(1\),在\(Rt△ABC\)中,\(∠C=90°\),\(BC=3\),\(AC=6\),\(D\),\(E\)分别是\(AC\),\(AB\)上的点,且\(DE∥BC\),\(DE=2\),将\(△ADE\)沿\(DE\)折起到\(△A_1 DE\)的位置,使\(A_1 C⊥CD\),如图\(2\).
(1)求证:\(A_1 C⊥\)平面\(BCDE\);
(2)线段\(BC\)上是否存在点\(P\),使平面\(A_1 DP\)与平面\(A_1 BE\)垂直?说明理由.

5(★★★)在如图所示的几何体中,面\(CDEF\)为正方形,面\(ABCD\)为等腰梯形,\(AB∥CD\),\(AB=2BC\),\(∠ABC=60°\),\(AC⊥FB\).
(1)求证:\(AC⊥\)平面\(FBC\);
(2)线段\(ED\)上是否存在点\(Q\),使平面\(EAC⊥\)平面\(QBC\)?证明你的结论.

答案
1.\(\dfrac{3}{2}\)
2.\(-1\)或\(4\)
3. 证明略
4. (1)证明略 (2)不存在
5. (1)证明略 (2)不存在


 浙公网安备 33010602011771号
浙公网安备 33010602011771号