1.3.(2) 建立空间直角坐标系和确定点坐标的方法
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)
选择性必修第一册同步提高，难度3颗星！
模块导图
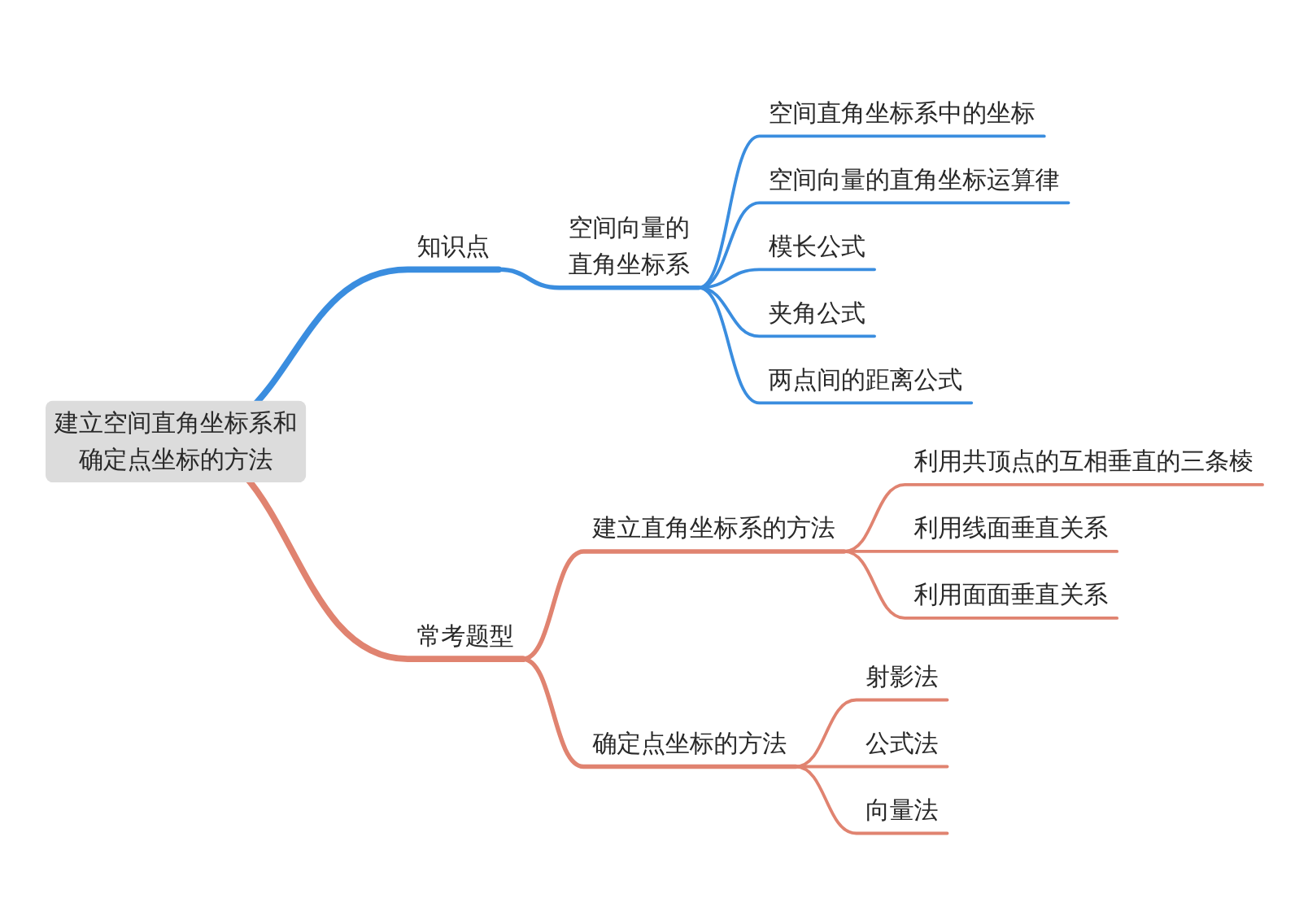
知识剖析
1空间向量的直角坐标系
(1) 空间直角坐标系中的坐标
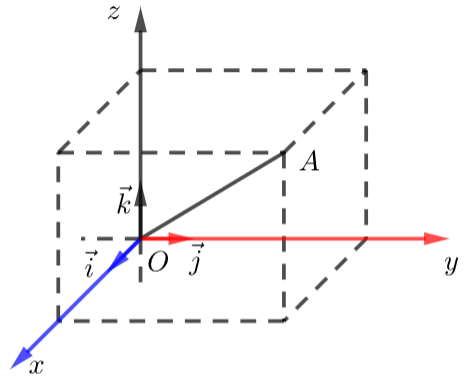
在空间直角坐标系\(O-xyz\)中，对空间任一点\(A\)，存在唯一的有序实数组\((x,y,z)\)，使\(\overrightarrow{O A}=x \vec{\imath}+y \vec{\jmath}+z \vec{k}\)，有序实数组\((x,y,z)\)叫作向量\(A\)在空间直角坐标系中的坐标，记作\(A(x,y,z)\)，\(x\)叫横坐标，\(y\)叫纵坐标，\(z\)叫竖坐标.
(2) 空间向量的直角坐标运算律
① 若\(: \vec{a}=\left(a_{1}, a_{2}, a_{3}\right)\)，\(\vec{b}=\left(b_{1}, b_{2}, b_{3}\right)\)，
则\(\vec{a}+\vec{b}=\left(a_{1}+b_{1}, a_{2}+b_{2}, a_{3}+b_{3}\right)\)，\(\vec{a}-\vec{b}=\left(a_{1}-b_{1}, a_{2}-b_{2}, a_{3}-b_{3}\right)\)，
\(\lambda \vec{a}=\left(\lambda a_{1}, \lambda a_{2}, \lambda a_{3}\right) \quad(\lambda \in R)\)，
\(\vec{a} \cdot \vec{b}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}\)，
\(\vec{a} \| \vec{b} \Rightarrow a_{1}=\lambda b_{1}\),\(a_{2}=\lambda b_{2}\)，\(a_{3}=\lambda b_{3}(\lambda \in R)\)，
\(\vec{a} \perp \vec{b}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}=0\)，
② 若\(A(x_1,y_1,z_1 )\),\(B(x_2,y_2,z_2 )\)，则\(\overrightarrow{A B}=\left(x_{2}-x_{1}, y_{2}-y_{1}, z_{2}-z_{1}\right)\).
③ 模长公式
若\(\vec{a}=\left(a_{1}, a_{2}, a_{3}\right)\)，则\(|\vec{a}|=\sqrt{\vec{a} \cdot \vec{a}}=\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}\).
④ 夹角公式
\(\cos \langle\vec{a}, \vec{b}\rangle=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot|\vec{b}|}=\dfrac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}} \sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}\)
\(∆ABC\)中,\(\overrightarrow{A B} \cdot \overrightarrow{A C}>0 \Rightarrow\)\(A\)为锐角,\(\overrightarrow{A B} \cdot \overrightarrow{A C}<0 \Rightarrow\)\(A\)为钝角.
⑤ 两点间的距离公式
若\(A(x_1,y_1,z_1)\),\(B(x_2,y_2,z_2)\)
则\(|\overrightarrow{A B}|=\sqrt{\overrightarrow{A B}^{2}}=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)
或\(d_{A B}=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\).
2 建立直角坐标系的方法
\((1)\)利用共顶点的互相垂直的三条棱构建直角坐标系
\((2)\)利用线面垂直关系构建直角坐标系
\((3)\)利用面面垂直关系构建直角坐标系
3 确定空间直角坐标系中点坐标的方法
求点的坐标和设点坐标的方法是一致的，常见方法具体如下
(1) 射影法
看所求点分别在\(x\)，\(y\)，\(z\)轴的投影对应的数值.
如求点\(P\)横坐标\(x\)，过点\(P\)作\(PP_1⊥\)平面\(xoy\)，再过点\(P_1\)作\(P_1 P_2⊥x\)轴，看点\(P_2\)对应数值即是\(x\)；
或直接构造长方体\(OP\)，即求出线段\(P_1 P_3\)、\(P_1 P_2\)、\(PP_1\)长度，再注意下正负号可得点\(B\)坐标.
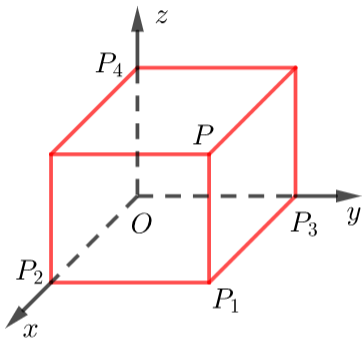
一般地，点在平面\(xOy\)、\(xOz\)、\(yOz\)或易得点在\(x\)，\(y\)，\(z\)轴的投影均适合射影法；
(2) 公式法
对中点、\(n\)等分点、重心等点可用公式求解；
若点\(A(x_1,y_1,z_1 )\)，\(B(x_2,y_2,z_2 )\)，\(C(x_3,y_3,z_3 )\)，
则线段\(AB\)的中点坐标\(\left(\dfrac{x_{1}+x_{2}}{2}, \dfrac{y_{1}+y_{2}}{2}, \dfrac{z_{1}+z_{2}}{2}\right)\)；三角形\(ABC\)的重心\(\left(\dfrac{x_{1}+x_{2}}{3}, \dfrac{y_{1}+y_{2}}{3}, \dfrac{z_{1}+z_{2}}{3}\right)\)；
点\(P\)在线段\(AB\)上且\(AP=λPB\)，则\(P\left(\dfrac{x_{1}+\lambda x_{2}}{1+\lambda}, \dfrac{y_{1}+\lambda y_{2}}{1+\lambda}, \dfrac{z_{1}+\lambda z_{2}}{1+\lambda}\right)\).
(3) 向量法
\((i)\)利用平行、垂直关系求某向量的坐标，再求点坐标；
\((ii)\)利用三角形法则或平行四边形法则，求出某向量的坐标，再求点坐标；
\((iii)\)三点共线问题：如若点\(A(x_1,y_1,z_1 )\),\(B(x_2,y_2,z_2 )\)，若点\(C\)在线段\(AB\)上，则可设\(\overrightarrow{A C}=\lambda \overrightarrow{A B}\)，利用待定系数法\(C(x,y,z)\)求出\(x\)，\(y\)，\(z\)！
(4) 几何法 把空间问题转化为平面问题，常见于利用相似三角形的性质.
(5) 待定系数法 设点\(P(x,y,z)\)，利用已知条件求出\(x\)，\(y\)，\(z\).
(6) 函数法 常用于设动点坐标；
动点\(P(a,b,c)\)在定直线\(AB\)上，把\(AB\)投影到空间坐标系中某个平面，如投影平面\(xoy\)，得到投影直线\(A'B'\)方程，从而达到动点\(P\)投影\(P'(a,b)\)中\(a\)，\(b\)的关系.
以上的方法其实也是相通的，也还存在其他一些灵活的处理方法(比如平移法等)，都需要理解再灵活运用.
经典例题
【题型一】建立直角坐标系的方法
利用共顶点的互相垂直的三条棱构建直角坐标系
【典题1】如图，已知直四棱柱\(ABCD－A_1 B_1 C_1 D_1\)中，\(AA_1=2\)，底面\(ABCD\)是直角梯形，\(∠A\)为直角，\(AB∥CD\)，\(AB=4\)，\(AD=2\)，\(DC=1\)，求异面直线\(BC_1\)与\(DC\)所成角的余弦值．
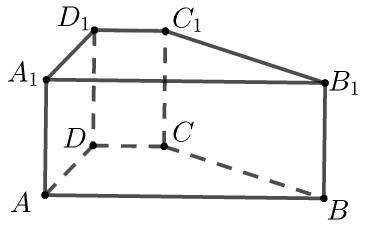
【解析】易得\(DA\)、\(DC\)、\(DD_1\)三线两两垂直，
如图，以\(D\)为坐标原点，分别以\(DA\)、\(DC\)、\(DD_1\)所在直线为\(x\)，\(y\)，\(z\)轴建立空间直角坐标系.
(后面解析省略)
利用线面垂直关系构建直角坐标系
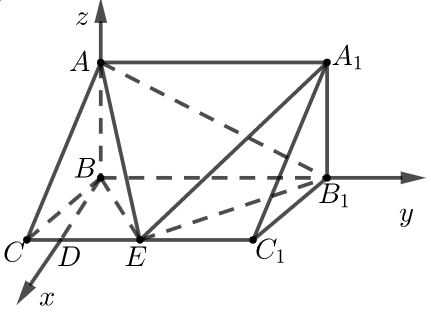
【典题2】如图，在三棱柱\(ABC－A_1 B_1 C_1\)中，\(AB⊥\)侧面\(BB_1 C_1 C\)，\(E\)为棱\(CC_1\)上异于\(C\)、\(C_1\)的一点，\(EA⊥EB_1\)．已知\(A B=\sqrt{2}\)，\(BB_1=2,BC=1\)，\(\angle B C C_{1}=\dfrac{\pi}{3}\)．求二面角\(A－EB_1－A_1\)的平面角的正切值．
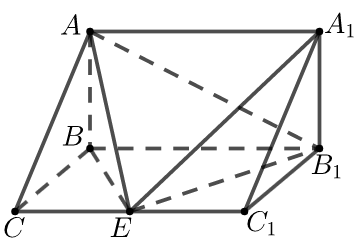
【解析】\(AB⊥\)侧面\(BB_1 C_1 C\)，而\(BC\)与\(BB_1\)不垂直，原图没三条两两垂直直线，此时在平面\(BB_1 C_1 C\)上过\(B\)点作垂直\(BB_1\)的直线，便得\(BD\)、\(BB_1\)、\(BA\)三线两两垂直，
如图，以\(B\)为原点，分别以\(BD\)、\(BB_1\)、\(BA\)所所在直线为\(x\)，\(y\)，\(z\)轴建立空间直角坐标系．
(后面解析省略)
利用面面垂直关系构建直角坐标系
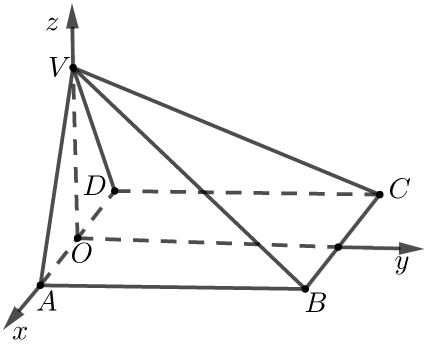
【典题3】如图，在四棱锥\(V－ABCD\)中，底面\(ABCD\)是正方形，侧面\(VAD\)是正三角形，平面\(VAD⊥\)底面\(ABCD\)．求面\(VAD\)与面\(VDB\)所成的二面角的余弦值．
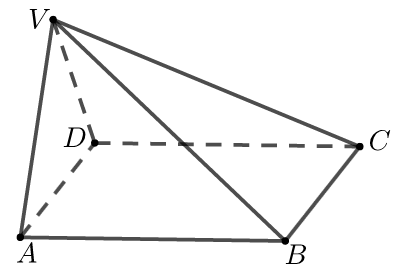
【解析】取\(AD\)的中点\(O\)，连接\(VO\)，
\(∵∆VAD\)是正三角形，\(∴VO⊥AD\)
又\(∵\)平面\(VAD⊥\)底面\(ABCD\)\(∴VO⊥\)平面\(ABCD\)
则以点\(O\)为原点，分别以\(OA\)、\(OV\)所在直线为\(x\)、\(z\)轴，以过点\(O\)作\(AD\)的垂线所在直线为\(y\)轴，建立如图所示的空间直角坐标系．
【点拨】
① 同一道题目中建系的方法不是唯一，是优是劣取决于关键点的坐标是否好求；
② 建系最根本的想法是找到两两垂直的三线，多关注题中有垂直关系的量，
(1) 垂直关系：长方体模型、等腰三角形的三线合一、菱形对角线相互垂直等；
(2) 若有线面垂直，则可考虑该面为平面\(xOy\)、\(xOz\)、\(yOz\)之一；
(3) 若有面面垂直，则可考虑两面为平面\(xOy\)、\(xOz\)、\(yOz\)其中两个.
③ 若是分别以\(OA\)、\(OB\)、\(OC\)所所在直线为\(x\)，\(y\)，\(z\)轴建立空间直角坐标系，则要先证明\(OA\)、\(OB\)、\(OC\)三线两两垂直，需要严谨些，不能想当然.
巩固练习
1(★)如图，在直三棱柱\(ABC－A_1 B_1 C_1\)中，\(A_1 B_1=A_1 C_1\)，\(F\)为\(B_1 C_1\)的中点，\(D\)，\(E\)分别是棱\(BC\)，\(CC_1\)上的点，且\(AD⊥BC\)，如何建立空间直角坐标系呢？
2(★)如图，已知四棱锥\(P－ABCD\)的底面\(ABCD\)为等腰梯形，\(AB∥DC\)，\(AC⊥BD\)，\(AC\)与\(BD\)相交于点\(O\)，且顶点\(P\)在底面上的射影恰为\(O\)点，如何建立空间直角坐标系呢？
3(★★)如图，三棱锥\(V－ABC\)的侧棱长都相等，底面\(ABC\)与侧面\(VAC\)都是以\(AC\)为斜边的等腰直角三角形，如何建立空间直角坐标系呢？
参考答案
- 以\(D\)为原点，分别以\(BD\)、\(DA\)、\(DF\)所在的直线为\(x\)，\(y\)，\(z\)轴建立空间直角坐标系.
- 以\(O\)为原点，分别以\(OB\)、\(OA\)、\(OP\)所在的直线为\(x\)，\(y\)，\(z\)轴建立空间直角坐标系.
- 取\(AC\)中点\(E\)，以\(E\)为原点，分别以\(EB\)、\(EC\)、\(EV\)所在的直线为\(x\)，\(y\)，\(z\)轴建立空间直角坐标系.
【题型二】确定空间直角坐标系中点坐标的方法
情况1 求点的坐标
【典题1】在平行六面体\(ABCD-A_1 B_1 C_1 D_1\)中，底面\(ABCD\)是矩形，\(AB=4\)，\(AD=2\)， 平行六面体高为\(2 \sqrt{3}\)，顶点\(D\)在底面\(A_1 B_1 C_1 D_1\)的射影\(O\)是\(C_1 D_1\)中点，设\(△AB_1 D_1\)的重心\(G\)，建立适当空间直角坐标系并写出下列点的坐标.
(1)\(A_1\)、\(B_1\)、\(A\)、\(D_1\)；
(2)\(G\)；
(3)\(B\)；
(4)若\(N\)为\(DD_1\)上点，且\(ON⊥ DD_1\)写出\(N\)坐标；
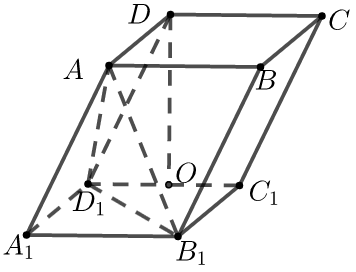
【解析】如图，以\(O\)为坐标原点，分别以\(OC_1\)、\(OD\)所在直线为\(y\)，\(z\)轴，以过点\(O\)作\(B_1 C_1\)的平行线为\(x\)轴建立空间直角坐标系．
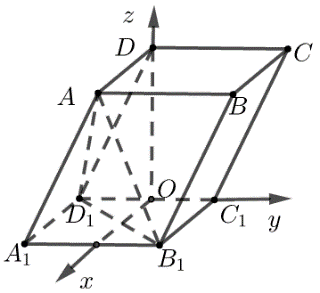
\({\color{Red}{ (1)射影法 }}\)
求点\(A_1 (x,y,z)\)，在平面\(xoy\)上则\(z=0\)，
由图可知它到\(y\)轴投影\(D_1\)对应数值\(-2\)，则\(y=-2\)，
到\(x\)轴投影对应数值为\(2\)，则\(x=2\)，即\(A_1 (2,-2,0)\)；
同理得\(B_1 (2,2,0)\)、\(A(2,0,2 \sqrt{3})\)、\(D_1 (0,-2,0)\)；
\({\color{Red}{ (2)公式法}}\)
\(∵G\)是\(△AB_1 D_1\)的重心，
\(\therefore G=\left(\dfrac{2+2+0}{3}, \dfrac{2+0-2}{3}, \dfrac{0+2 \sqrt{3}+0}{3}\right)=\left(\dfrac{4}{3}, 0, \dfrac{2 \sqrt{3}}{3}\right)\)
\({\color{Red}{(由三角形重心公式 \left(\dfrac{x_{1}+x_{2}+x_{3}}{3}, \dfrac{y_{1}+y_{2}+y_{3}}{3}, \dfrac{z_{1}+z_{2}+z_{3}}{3}\right) 可得) }}\)
\({\color{Red}{ (3)向量法}}\)
设\(B ( x,y,z )\)，则\(\overrightarrow{B_{1} B}=(x-2, y-2, z)\)，\(\overrightarrow{D_{1} D}=(0,2,2 \sqrt{3})\)，
又\(\because \overrightarrow{B_{1} B}=\overrightarrow{D_{1} D}\)，
\({\color{Red}{ (利用向量平行关系)}}\)
比较得\(x=2\)，\(y=4\)，\(z=2 \sqrt{3}\)，
\(∴\)点\(B\)坐标为\((2,4,2 \sqrt{3})\) \({\color{Red}{ (投影法也可以)}}\)
(4)\(∵D_1\)、\(N\)、\(D\)三点共线，可设\(\overrightarrow{D_{1} N}=\lambda \overrightarrow{D D_{1}}\)，
\({\color{Red}{(某点在一直线上常用向量法) }}\)
即\(\overrightarrow{D_{1} N}=\lambda(0,2,2 \sqrt{3})=(0,2 \lambda, 2 \sqrt{3} \lambda)\)，
\(\therefore \overrightarrow{O N}=\overrightarrow{O D_{1}}+\overrightarrow{D_{1} N}=(0,2 \lambda-2,2 \sqrt{3} \lambda)\)，
\(\therefore N(0,2 \lambda-2,2 \sqrt{3} \lambda)\)，
\(\because \overrightarrow{O N} \cdot \overrightarrow{D_{1} D}=0\)，
\(\therefore 0+4(\lambda-1)+12 \lambda=0\)，解得\(\lambda=\dfrac{1}{4}\)，
故\(N\left(0,-\dfrac{3}{2}, \dfrac{\sqrt{3}}{2}\right)\).
\({\color{Red}{ (几何法也可以，求出点N到y，z轴的距离) }}\)
【点拨】
(1)射影法：看所求点分别在\(x\)，\(y\)，\(z\)轴的投影对应的数值；
一般地，点在平面\(xOy\)、\(xOz\)、\(yOz\)或易得点在\(x\)，\(y\)，\(z\)轴的投影均适合射影法；
② 公式法：对中点、\(n\)等分点、重心等点可用公式求解；
③ 向量法：常用于涉及到平行、垂直、共线等向量关系中的点.
各方法之间也是相通的，需要理解再灵活运用.
【典题2】如图，矩形\(ABCD\)中，\(2BC=CD\)，\(E\)为\(CD\)的中点，以\(BE\)为折痕把四边形\(ABED\)折起，使\(A\)达到\(P\)的位置，且\(PC⊥BC\),\(M\)，\(N\)，\(F\)分别为\(PB\)，\(BC\)，\(EC\)的中点．建系求点\(P\)的坐标.
【解析】设\(BC=2\)，则\(BN=CN=1\)，\(CF=EF=1\)，
以\(C\)为原点，\(CB\)为\(x\)轴，\(CE\)为\(y\)轴，过\(C\)作平面\(BCE\)的垂直\(CQ\)为\(z\)轴，建立空间直角坐标系，
则\(B(2,0,0)\)，\(E(0,2,0)\)，\(F(0,1,0)\)，
设\(P(x,y,z)\)，\(PB=CD=2BC=4\)，
则\(J P E=\sqrt{P D^{2}+D E^{2}}=\sqrt{2^{2}+2^{2}}=2 \sqrt{2}\)，\(P C=\sqrt{P B^{2}-B C^{2}}=\sqrt{4^{2}-2^{2}}=2 \sqrt{3}\)，
\(\therefore\left\{\begin{array}{l}
(x-2)^{2}+y^{2}+z^{2}=16 \\
x^{2}+(y-2)^{2}+z^{2}=8 \\
x^{2}+y^{2}+z^{2}=12
\end{array}\right.\)，解得\(x=0\)，\(y=2\)，\(z=2 \sqrt{2}\)，
\(\therefore P(0,2,2 \sqrt{2})\).
\({\color{Red}{(不同的建系，坐标当然不同，这里主要介绍待定系数法求点坐标) }}\)
【点拨】利用待定系数法，设\(P(x,y,z)\)，再利用两点距离公式求得点的坐标.
情况2 设点坐标
【典题3】长方形\(ABCD\)中，\(AB=2AD\)，\(M\)是\(CD\)中点(图1)，将\(∆ADM\)沿\(AM\)折起，使得\(AD⊥BM\)(图\(2\))在图\(2\)中
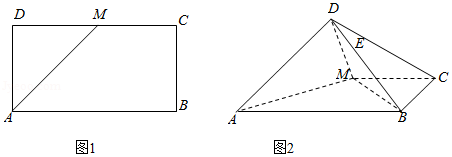
(1)求证：平面\(ADM⊥\)平面\(ABCM\)；
(2)在线段\(BD\)上是否存点\(E\)，使得二面角\(E-AM-D\)的余弦值为\(\dfrac{\sqrt{5}}{5}\)，说明理由．
【解析】(1)证明：在长方形\(ABCD\)中，由\(A B=2 A D=2 \sqrt{2}\)，\(M\)是\(DC\)中点，
得\(AM=BM=2\)，而\(A B=2 \sqrt{2}\)，
\(∴AM^2+BM^2=AB^2\)，得\(BM⊥AM\)，
又\(AD⊥BM\)，且\(AD∩AM=A\)，\(∴BM⊥\)平面\(ADM\)，
而\(BM⊂\)平面\(ABCD\)，
\(∴\)平面\(ADM⊥\)平面\(ABCM\)；
(2) \({\color{Red}{思路：先根据“点E(a,b,c)在线段BD上”，得到其坐标形式(即找到a,b,c的关系)，再利用二面角余弦值求出点E的坐标；那怎么引入参数设出点E坐标呢？ }}\)
解：取\(AB\)中点\(N\)，以\(M\)为坐标原点，分别以\(MN\)，\(MC\)所在直线为\(x\)，\(y\)轴，
在平面\(ADM\)内，过\(M\)作底面垂线为\(z\)轴，建立空间直角坐标系，
则\(M(0,0,0)\)，\(A(\sqrt{2},-1,0)\)，\(D\left(\dfrac{\sqrt{2}}{2},-\dfrac{1}{2}, 1\right)\)，\(B(\sqrt{2}, 1,0)\)，
\(\overrightarrow{M A}=(\sqrt{2},-1,0)\)，\(\overrightarrow{M D}=\left(\dfrac{\sqrt{2}}{2},-\dfrac{1}{2}, 1\right)\)，
\({\color{Red}{方法1 \quad向量法 }}\)
设\(E\)为线段\(BD\)上的点，
则\(\overrightarrow{D E}=\lambda \overrightarrow{D B}=\left(\dfrac{\sqrt{2}}{2} \lambda, \dfrac{3}{2} \lambda,-\lambda\right)(0 \leq \lambda \leq 1)\)，
\(\overrightarrow{M E}=\overrightarrow{D E}-\overrightarrow{D M}=\left(\dfrac{\sqrt{2}}{2} \lambda+\dfrac{\sqrt{2}}{2}, \dfrac{3}{2} \lambda-\dfrac{1}{2}, 1-\lambda\right)\)，
\({\color{Red}{ (即得到点E坐标)}}\)
\({\color{Red}{(以上是由共线关系利用向量法引入参数λ设点E坐标) }}\)
\({\color{Red}{(PS 以下求λ的过程学完求二面角的向量法方能理解) }}\)
设平面\(AMD\)的一个法向量为\(\vec{m}=\left(x_{1}, y_{1}, z_{1}\right)\)，平面\(EAM\)的一个法向量为\(\vec{n}=\left(x_{2}, y_{2}, z_{2}\right)\)，
由\(\left\{\begin{array}{l}
\vec{m} \cdot \overrightarrow{M A}=\sqrt{2} x_{1}-y_{1}=0 \\
\vec{m} \cdot \overrightarrow{M D}=\dfrac{\sqrt{2}}{2} x_{1}-\dfrac{1}{2} y_{1}+z_{1}=0
\end{array}\right.\)，
取\(y_{1}=\sqrt{2}\)，得\(\vec{m}=(1, \sqrt{2}, 0)\)；
由\(\left\{\begin{array}{l}
\vec{n} \cdot \overrightarrow{M A}=\sqrt{2} x_{2}-y_{2}=0 \\
\vec{n} \cdot \overrightarrow{M E}=\left(\dfrac{\sqrt{2}}{2} \lambda+\dfrac{\sqrt{2}}{2}\right) x_{2}+\left(\dfrac{3}{2} \lambda-\dfrac{1}{2}\right) y_{2}+(1-\lambda) z_{2}=0
\end{array}\right.\)，
取\(y_{2}=\sqrt{2}\)，得\(\vec{n}=\left(1, \sqrt{2}, \dfrac{2 \sqrt{2} \lambda}{\lambda-1}\right)\)．
由\(\cos <\vec{m}, \vec{n}>=\dfrac{\vec{m} \cdot \vec{n}}{|\vec{m}||\vec{n}|}=\dfrac{3}{\sqrt{3} \times \sqrt{3+\dfrac{8 \lambda^{2}}{(\lambda-1)^{2}}}}=\dfrac{\sqrt{5}}{5}\)，
解得\(\lambda=3+\sqrt{6}\)(舍)或\(\lambda=3-\sqrt{6} \in[0,1]\)．
\(∴\)在线段\(BD\)上存点\(E\)，使得二面角\(E-AM-D\)的余弦值为\(\dfrac{\sqrt{5}}{5}\)．
\({\color{Red}{方法2 \quad函数法 }}\)
设\(E(a,b,c)\)，
\(\because D\left(\dfrac{\sqrt{2}}{2},-\dfrac{1}{2}, 1\right)\)，\(B(\sqrt{2}, 1,0)\)，
\(∴\)点\(B\)、\(D\)、\(E\)在平面\(xoy\)上投影为\(B^{\prime}(\sqrt{2}, 1)\)、\(D^{\prime}\left(\dfrac{\sqrt{2}}{2},-\dfrac{1}{2}\right)\)，\(E^{\prime}(a, b)\)，
\({\color{Red}{(相当于把直线BD投影到平面xoy上，空间问题化为平面问题，降维处理)
}}\)
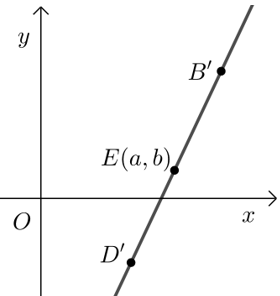
求得直线\(B'D'\)的方程为\(y=\dfrac{3 \sqrt{2}}{2} x-2\)，则\(b=\dfrac{3 \sqrt{2}}{2} a-2\)；
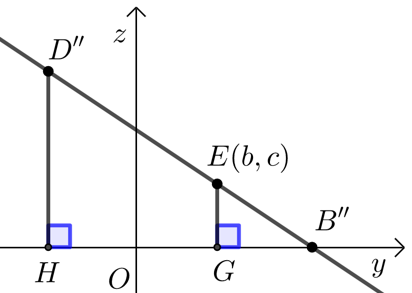
点\(B\)、\(D\)、\(E\)在平面\(yoz\)上投影为\(B^{\prime \prime}(1,0)\)、\(D^{\prime \prime}\left(-\dfrac{1}{2}, 1\right)\)，\(E^{\prime \prime}(b, c)\)，
求得直线\(B^{\prime \prime} D^{\prime \prime}\)的方程为\(z=-\dfrac{2}{3} y+\dfrac{2}{3}\)，
则\(c=-\dfrac{2}{3} b+\dfrac{2}{3}\)，即\(c=-\sqrt{2} a+2\)；
所以\(E\)的坐标可设为\(\left(a, \dfrac{3 \sqrt{2}}{2} a-2,-\sqrt{2} a+2\right)\)，
以下求解类似方法1！
【点拨】
① 本题在处理“点\(E\)在线段\(BD\)上”这一条件时，想设点\(E(a,b,c)\)找到\(a\),\(b\),\(c\)的关系，介绍了向量法和函数法，而向量法引入变量\(λ\)表示\(a\),\(b\),\(c\)，而函数法变量是\(a\)，用其表示\(b\),\(c\)便可；
② 有时也可用几何法相似求解，
比如在方法2中求\(E(a,b,c)\)中\(b\)、\(c\)的关系，
如下图，过点\(D^{\prime \prime}\)、\(E\)分别作\(D^{\prime \prime} H \perp x\)轴，\(EG⊥x\)轴，
由\(\Delta D^{\prime \prime} H B^{\prime \prime} \sim \Delta E G B^{\prime \prime}\)得\(\dfrac{D^{\prime \prime} H}{E G}=\dfrac{B^{\prime \prime} H}{B^{\prime \prime} G} \Rightarrow \dfrac{1}{c}=\dfrac{3}{2(1-b)} \Rightarrow c=-\dfrac{2}{3} b+\dfrac{2}{3}\).
巩固练习
1(★★)一张平行四边形的硬纸\(ABC_0 D\)中，\(AD=BD=1\)，\(A B=\sqrt{2}\).沿它的对角线\(BD\)折起，使点\(C_0\)到达平面外\(C\)点的位置.若\(\cos \angle C A B=\dfrac{3}{4}\)，建系求点\(C\)的坐标.
2(★★)四棱锥\(S-ABCD\)中，\(AB∥CD\)，\(BC⊥CD\)，侧面\(SAB\)为等边三角形，\(AB=BC=2\)，\(CD=SD=1\).建系求点\(S\)的坐标.
3(★★)在四棱锥\(P-ABCD\)中，底面\(ABCD\)是正方形，侧棱\(PD\)垂直于底面\(ABCD\)，\(PD=DC\),\(E\)是\(PC\)的中点，\(F\)在\(PB\)上，若\(EF⊥PB\)于点\(F\)，试求点\(F\)的坐标.
参考答案
-
， 如图建系，则\(C\left(\dfrac{1}{2}, 1, \dfrac{\sqrt{3}}{2}\right)\). -
， 如图建系，则\(S\left(1, \dfrac{1}{2}, \dfrac{\sqrt{3}}{2}\right)\). -
如图建系，则$F\left(\dfrac{2}{3}, \dfrac{2}{3}, \dfrac{4}{3}\right)$.
(点的坐标与建系的方法有关)
