专题 直线系方程与圆系方程

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

选择性必修第一册同步提高，难度3颗星！

模块导图

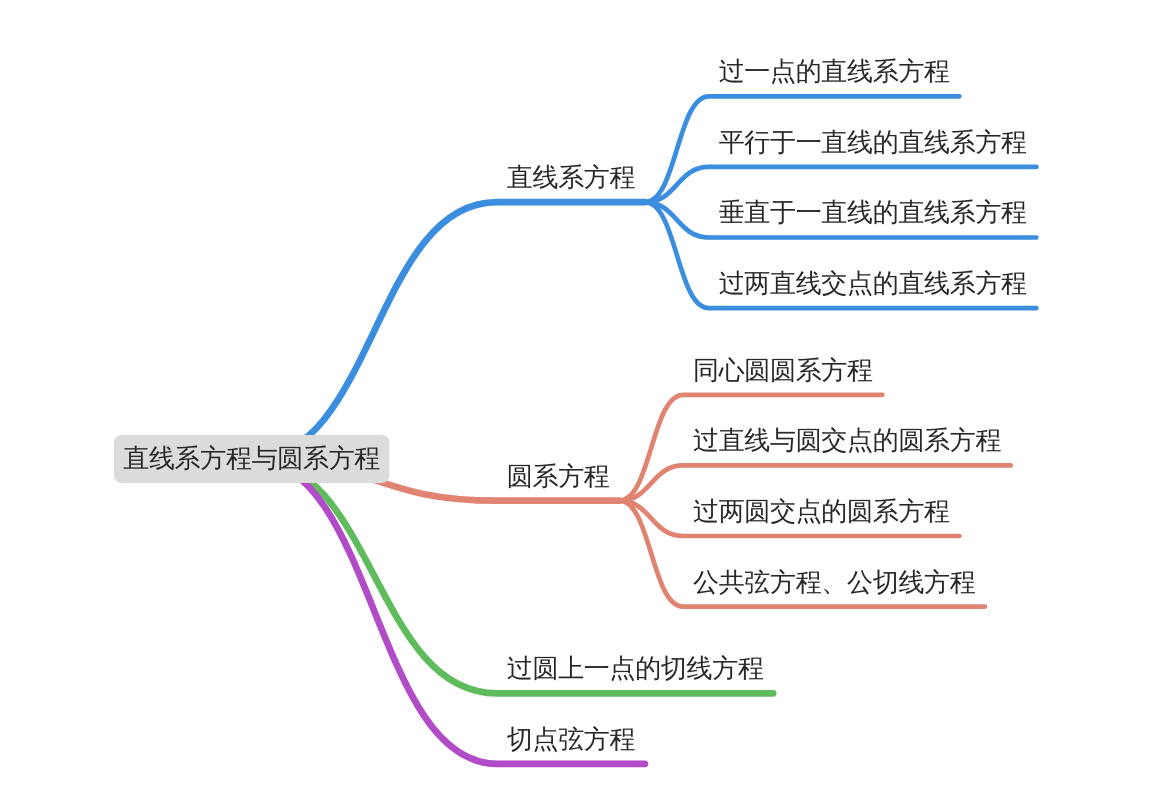
知识剖析

直线系方程

\((1)\)过点\((x_0 ,y_0)\)的直线系方程为\(A(x-x_0 )+B(y-y_0 )=0\)(其中\(A\),\(B\)不全为零)
\((2)\)平行于直线\(Ax+By+C=0\)的直线系方程\(Ax+By+C_0=0(C≠C_0)\)；
\((3)\)垂直于直线\(Ax+By+C=0\)的直线系方程\(Bx-Ay+C_0=0\)；
\((4)\)过两条已知直线\(l_1:A_1 x+B_1 y+C_1=0\)和\(l_2:A_2 x+B_2 y+C_2=0\)交点的直线系方程\(A_1 x+B_1 y+C_1+λ(A_2 x+B_2 y+C_2 )=0\)
(\(λ∈R\), 这个直线系下不包括直线\(l_2:A_2 x+B_2 y+C_2=0\)，解题时注意检验\(l_2\)是否满足题意)
 

圆系方程

\((1)\)以\((a ,b)\)为圆心的同心圆圆系方程：\((x-a)^2+(y-b)^2=λ(λ>0)\)；
\((2)\)与圆\(x^2+y^2+Dx+Ey+F=0\)同心圆的圆系方程为\(x^2+y^2+Dx+Ey+λ=0\)；
\((3)\)过直线\(Ax+By+C=0\)与圆\(x^2+y^2+Dx+Ey+F=0\)交点的圆系方程为\(x^2+y^2+Dx+Ey+F+λ(Ax+By+C)=0(λ∈R)\)；
\((4)\)过两圆\(C_1：x^2+y^2+D_1 x+E_1 y+F_1=0\)，\(C_2：x^2+y^2+D_2 x+E_2 y+F_2=0\)交点的圆系方程为\(x^2+y^2+D_1 x+E_1 y+F_1+λ(x^2+y^2+D_2 x+E_2 y+F_2 )=0\)
(\(λ≠-1\), 此圆系不含\(C_2：x^2+y^2+D_2 x+E_2 y+F_2=0\))
特别地，当\(λ=-1\)时，上述方程为一次方程.
两圆相交时，表示公共弦方程；两圆相切时，表示公切线方程.
 

过圆上一点的切线方程

过圆上一点\(P(x_0 ,y_0)\)作圆\(\odot M:(x-a)^2+(y-b)^2=r^2\)的切线\(l\)方程为
\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\\\)
\({\color{Red}{证明 \quad 向量法 }}\)

向量\(\overrightarrow{P M}=\left(a-x_{0}, b-y_{0}\right)\)，设切线上任意一点\(B(x ,y)\)，
\(∵l⊥PM\)，\(\therefore \overrightarrow{P M} \perp \overrightarrow{P B}\)，即\(\overrightarrow{P M} \cdot \overrightarrow{P B}=0 \text {, }\)，
\(∴(a-x_0 ,b-y_0 )(x-x_0 ,y-y_0 )=0\)
\(⇒(a-x_0)(x-x_0)+(b-y_0)(y-y_0)=0\)
即切线\(l\)方程为\((a-x_0)(x-x_0)+(b-y_0)(y-y_0)=0\).
\(∵(a-x_0 )(x-x_0 )+(b-y_0 )(y-y_0 )=0\)
\(⇒(a-x_0 )(x-a+a-x_0 )+(b-y_0 )(y-b+b-y_0 )=0\)
\(⇒(a-x_0 )(x-a)+(a-x_0 )^2+(b-y_0 )(y-y_0 )+(b-y_0 )^2=0\)
\(⇒(a-x_0 )(x-a)+(b-y_0 )(y-y_0 )+r^2=0\)
\(⇒(x_0-a)(x-a)+(y_0-b)(y-b)=r^2\)
\(∴\)切线\(l\)方程也可以写成\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\).
 

切点弦方程

过圆\(\odot M:(x-a)^2+(y-b)^2=r^2\)外一点\(P(x_0 ,y_0)\)引圆的两条切线，切点分别是\(A\)、\(B\)，则直线\(AB\)的方程为\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\).

\({\color{Red}{ 证明}}\)

\({\color{Red}{ 方法1}}\) 设切点\(A(x_1,y_1 )\)，
则过点\(A\)的切线方程为\((x-a)(x_1-a)+(y-b)(y_1-b)=r^2\)，
由于点\(P(x_0 ,y_0)\)在切线\(PA\)上，所以有\((x_0-a)(x_1-a)+(y_0-b)(y_1-b)=r^2\)①，
设切点\(B(x_2,y_2 )\)，同理得\((x_0-a)(x_2-a)+(y_0-b)(y_2-b)=r^2\)②，
由①②得点\(A\)与点\(B\)在直线\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\)上，
则直线\(AB\)的方程为\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\).
\({\color{Red}{ 方法2}}\) 以\(MP\)为直径的圆方程为\((x-a)(x-x_0 )+(y-b)(y-y_0 )=0\)，记为圆\(C\)，
因为\(\angle P A M=\angle P B M=\dfrac{\pi}{2}\)，所以点\(A\)、\(B\)在圆\(C\)上，
则\(A\)、\(B\)是圆\(C\)与圆\(M\)的两个交点，
由圆系方程可知，两圆方程相减即得直线\(AB\)方程
\((x_0-a)(x-a)+(y_0-b)(y-b)=r^2\)
\({\color{Red}{ (这跟圆上点的切线方程形式一致)}}\)
 

经典例题

【题型一】直线系方程

【典题1】求过两直线\(x-2y+4=0\)和\(x+y-2=0\)的交点\(P\)，且分别满足下列条件的直线\(l\)的方程．
(1)过点\((2 ,1)\)；
(2)和直线\(3x-4y+5=0\)垂直．
【解析】由\(\left\{\begin{array}{l} x-2 y+4=0 \\ x+y-2=0 \end{array}\right.\)解得\(\left\{\begin{array}{l} x=0 \\ y=2 \end{array}\right.\)，\(∴P(0 ,2)\)．
(1) \({\color{Red}{ 方法一}}\) 由两点的坐标求得斜率为\(k_{l}=\dfrac{2-1}{0-2}=-\dfrac{1}{2}\)，
由点斜式求得直线方程为\(y-2=-\dfrac{1}{2}(x-0)\)，
化简得\(x+2y－4=0\)．
\({\color{Red}{方法二 }}\) 设过点\(P\)的直线方程为\(x-2y+4+λ(x+y-2)=0\)，
\(∵\)过点\((2 ,1)\)，\(∴2-2+4+λ=0⇒λ=-4\)，
故所求直线方程为\(x-2y+4-4(x+y-2)=0⇒x+2y-4=0\).
(2) \({\color{Red}{方法一 }}\) 依题意得所求直线的斜率为\(k_{2}=-\dfrac{4}{3}\)，
由点斜式求得直线方程为\(y-2=-\dfrac{4}{3}(x-0)\)，即\(4x+3y-6=0\)．
\({\color{Red}{ 方法二}}\) 设所求直线为\(4x+3y+λ=0\)
\(∵\)过点\(P(0 ,2)\)，\(∴0+6+λ=0⇒λ=-6\)，
故所求直线方程为\(4x+3y-6=0\).
【点拨】此题是直线系问题.从本题来看，用直线系方程的方法求解对于一般的解法也没有优势，这里只是拓展大家的思路.
 

【典题2】求过点\(P(-1 ,4)\)，圆\((x-2)^2+(y-3)^2=1\)的切线\(l\)的方程．
【解析】\({\color{Red}{方法一 }}\) 当直线\(l\)斜率不存在时，方程为\(x=-1\)，显然不是切线，
故可设切线方程为\(y=k(x+1)+4\)，
\(∵\)直线\(l\)与圆相切，\(∴\)圆心\((2 ,3)\)到直线\(l\)的距离等于半径\(1\)，
故\(\dfrac{|3 k+1|}{\sqrt{1+k^{2}}}=1\)，解得\(k=0\)或\(-\dfrac{3}{4}\)，
故所求直线\(l\)的方程为\(y=4\)或\(3x+4y-13=0\)．
\({\color{Red}{方法二 }}\) 如方法二，设切线方程为\(y=k(x+1)+4\)，
由\(\left\{\begin{array}{c} y=k(x+1)+4 \\ (x-2)^{2}+(y-3)^{2}=1 \end{array}\right.\)得\((1+k^2 ) x^2+(2k^2+2k-4)x+k^2+2k-4=0\)
其判别式\(∆=(2k^2+2k-4)^2-4(1+k^2 )(k^2+2k-4)=0\), 解得\(k=0\)或\(-\dfrac{3}{4}\)，
故所求直线\(l\)的方程为\(y=4\)或\(3x+4y-13=0\)．
\({\color{Red}{方法三 }}\) 设所求直线的方程为\(A(x+1)+B(y-4)=0\)(其中\(A\)\(,B\)不全为零)，
\(∵\)直线\(l\)与圆相切，\(∴\)圆心\((2 ,3)\)到直线\(l\)的距离等于半径\(1\)，故\(\dfrac{|3 A-B|}{\sqrt{A^{2}+B^{2}}}=1\)
整理，得\(A(4A-3B)=0\)，即\(A=0\)(这时\(B≠0\))或\(A=\dfrac{3}{4}\)，\(B≠0\)．
故所求直线\(l\)的方程为\(y=4\)或\(3x+4y-13=0\)．
【点拨】本题的方法很多，这里利用了直线系方程，过点\((x_0 ,y_0)\)的直线系方程为\(A(x-x_0 )+B(y-y_0 )=0\)(其中\(A\),\(B\)不全为零) , 它比起斜截式\(y=kx+b\)的设法好在不用对\(k\)的存在进行讨论.
 

【题型二】圆系方程

【典题1】经过直线\(2x-y+3=0\)与圆\(x^2+y^2+2x-4y+1=0\)的两个交点，且面积最小的圆的方程是\(\underline{\quad \quad}\)．
【解析】\({\color{Red}{方法一 }}\) \({\color{Red}{ (面积最小的圆是以两个交点为直径的圆) }}\)
\(∵\)圆\(x^2+y^2+2x-4y+1=0\)的方程可化为\((x+1)^{2}+(y-2)^{2}=4\)．
\(∴\)圆心坐标为\((-1 ,2)\)，半径为\(r=2\)；
\(∴\)圆心到直线\(2x-y+3=0\)的距离为\(d=\dfrac{1}{\sqrt{5}}\)．
设直线\(2x-y+3=0\)和圆\(x^2+y^2+2x-4y+1=0\)的交点为\(A\),\(B\)．
则\(|A B|=2 \sqrt{r^{2}-d^{2}}=2 \sqrt{4-\dfrac{1}{5}}=\dfrac{2 \sqrt{19}}{\sqrt{5}}\)．
\(∴\)过点\(A\),\(B\)的最小圆半径为\(\dfrac{\sqrt{19}}{\sqrt{5}}\)．
联立\(\left\{\begin{array}{l} 2 x-y+3=0 \\ x^{2}+y^{2}+2 x-4 y+1=0 \end{array}\right.\)得\(5x^2+6x-2=0\)，
故\(x_{1}+x_{2}=-\dfrac{6}{5}\)，
则圆心的横坐标为\(\dfrac{1}{2}\left(x_{1}+x_{2}\right)=-\dfrac{3}{5}\)，纵坐标为\(2 \times\left(-\dfrac{3}{5}\right)+3=\dfrac{9}{5}\)，
\(∴\)最小圆的圆心为\(\left(-\dfrac{3}{5}, \dfrac{9}{5}\right)\)，
\(∴\)最小圆的方程为\(\left(x+\dfrac{3}{5}\right)^{2}+\left(y-\dfrac{9}{5}\right)^{2}=\dfrac{19}{5}\)．
\({\color{Red}{ 方法二}}\) 依题意，
可设过点\(A\)、\(B\)两点圆的方程为\(x^2+y^2+2x－4y+1+λ(2x-y+3)=0\)，
\({\color{Red}{(利用圆系方程把满足题意的所有圆表示出来，再用代数的方法求面积最小的圆) }}\)
整理得\((x+\lambda+1)^{2}+\left(y-\dfrac{4+\lambda}{2}\right)^{2}=\dfrac{5}{4} \lambda^{2}+\lambda+4\)
若要使得圆的面积最小，则只需半径最小，即\(\dfrac{5}{4} \lambda^{2}+\lambda+4\)取到最小值，
而\(\dfrac{5}{4} \lambda^{2}+\lambda+4=\dfrac{5}{4}\left(\lambda+\dfrac{2}{5}\right)^{2}+\dfrac{19}{5} \geq \dfrac{19}{5}\)，当\(\lambda=-\dfrac{2}{5}\)时取到最小值，
此时圆的方程为\(\left(x+\dfrac{3}{5}\right)^{2}+\left(y-\dfrac{9}{5}\right)^{2}=\dfrac{19}{5}\).
【点拨】本题是过直线与圆交点的圆系问题.方法一可以说是从几何的角度得出思路求解，而方法二算是“代数法”，略显简洁些.
 

【典题2】已知圆\(C_1：x^2+y^2=10\)与圆\(C_2：x^2+y^2+2x+2y-14=0\)．
(1)求证：圆\(C_1\)与圆\(C_2\)相交；
(2)求两圆公共弦所在直线的方程；
(3)求经过两圆交点，且圆心在直线\(x+y-6=0\)上的圆的方程．
【解析】(1)证明： \({\color{Red}{(圆心距C_1 C_2∈(R-r ,R+r)⇔ 两圆相交) }}\)
圆\(C_2：x^2+y^2+2x+2y-14=0\)化为标准方程为\((x+1)^{2}+(y+1)^{2}=16\)
\(∴C_2 (-1 ,-1)\)，\(r=4\)
\(∵\)圆\(C_1：x^2+y^2=10\)的圆心坐标为\((0 ,0)\)，半径为\(R=\sqrt{10}\)
\(\therefore\left|C_{1} C_{2}\right|=\sqrt{2}\),
\(\because 4-\sqrt{10}<\sqrt{2}<4+\sqrt{10},\)，\(∴\)两圆相交；
(2) \({\color{Red}{(两圆方程相减所得方程即是公共弦所在直线方程) }}\)
将两圆方程相减，可得\(2x+2y-4=0\)，
即两圆公共弦所在直线的方程为\(x+y-2=0\)；
(3) \({\color{Red}{ 方法一}}\) \({\color{Red}{(先求出两个交点，再求圆心与半径得圆的方程，思路很直接) }}\)
由\(\left\{\begin{array}{c} x^{2}+y^{2}+2 x+2 y-14=0 \\ x^{2}+y^{2}=10 \end{array}\right.\)解得\(\left\{\begin{array}{c} x=3 \\ y=-1 \end{array}\right.\)或\(\left\{\begin{array}{c} x=-1 \\ y=3 \end{array}\right.\)，
\({\color{Red}{(这里还是有些计算量的) }}\)
则交点为\(A(3 ,-1)\)\(,B(-1 ,3)\)，
\(∵\)圆心在直线\(x+y-6=0\)上，设圆心为\(P(6-n ,n)\)，
则\(AP=BP\)，解得\(n=3\)，
故圆心\(P(3 ,3)\)，半径\(r=AP=4\)，
\(∴\)所求圆的方程为\((x-3)^{2}+(y-3)^{2}=16\)．
\({\color{Red}{方法二 }}\) 设所求圆的方程为\(x^2+y^2+2x+2y-14+λ(x^2+y^2-10)=0(λ≠-1)\)
即\((1+\lambda) x^{2}+(1+\lambda) y^{2}+2 x+2 y-14-10 \lambda=0\)
\(∴\)圆心坐标为\(\left(-\dfrac{1}{1+\lambda},-\dfrac{1}{1+\lambda}\right)\)
代入直线\(x+y-6=0\)可得\(-\dfrac{1}{1+\lambda}-\dfrac{1}{1+\lambda}-6=0\)，\(\therefore \lambda=-\dfrac{4}{3}\)
\(∴\)所求圆的方程为\(x^2+y^2-6x-6y+2=0\)．
【点拨】此题是过圆与圆交点的圆系问题.
① 两圆之间的位置关系看圆心距\(O_1 O_2\)与两圆半径\(R\)与\(r\)之间的关系；
② 过两圆\(C_1：x^2+y^2+D_1 x+E_1 y+F_1=0\)，\(C_2：x^2+y^2+D_2 x+E_2 y+F_2=0\)交点的圆系方程为\(x^2+y^2+D_1 x+E_1 y+F_1+λ(x^2+y^2+D_2 x+E_2 y+F_2 )=0\)
(\(λ≠-1\), 此圆系不含\(C_2：x^2+y^2+D_2 x+E_2 y+F_2=0\))
特别地，当\(λ=-1\)(即两圆方程相减)时，上述方程为一次方程.
两圆相交时，表示公共弦方程；两圆相切时，表示公切线方程.
③ 方法的选取在于思考难度、计算量、严谨性性等.
 

【典题3】过点\((3 ,1)\)作圆\((x-1)^{2}+y^{2}=1\)的两条切线，切点分别为\(A\)、\(B\)，则直线\(AB\)的方程为\(\underline{\quad \quad}\) .
【解析】\({\color{Red}{方法一 }}\) 由图易得一切点为\((1 ,1)\)，
连接点\((3 ,1)\)与圆心\((1 ,0)\)直线的斜率\(k=\dfrac{1-0}{3-1}=\dfrac{1}{2}\)，
由切线性质可知\(k_{A B} \cdot k=-1 \Rightarrow k_{A B}=-2\)，
又直线\(AB\)过点\((1 ,1)\)
\(∴\)直线\(AB\)方程为\(y-1=-2(x-1)⇒2x+y-3=0\).
\({\color{Red}{(结合图形的特殊性，利用平几的知识求解，不具有一般性) }}\)
\({\color{Red}{方法二 }}\) 圆\((x-1)^{2}+y^{2}=1\)的圆心为\(C(1 ,0)\)，半径为\(1\)，
以\((3 ,1)\)、\(C(1 ,0)\)为直径的圆的方程为\((x-2)^{2}+\left(y-\dfrac{1}{2}\right)^{2}=\dfrac{5}{4}\)，
将两圆的方程相减可得公共弦AB的方程\(2x+y－3=0\)，
\({\color{Red}{(这里把直线AB看成是两个圆公共弦所在的直线) }}\)
\({\color{Red}{ 方法三 }}\)过圆\(\odot M:(x-a)^{2}+(y-b)^{2}=r^{2}\)外一点\(P(x_0 ,y_0)\)引圆的两条切线，
切点分别是\(A\)、\(B\), 则直线\(AB\)的方程为\((x-x_0 )(a-x_0 )+(y-y_0 )(b-y_0 )=r^2\).
所以有\((3+1)(x-1)+1\cdot y=1\)，化简得\(2x+y-3=0\)．
\({\color{Red}{(使用结论直接快捷) }}\)
【点拨】本题是圆的切点弦问题. 方法三直接快捷，但若是只会直接套用，达不到锻炼数学思维的能力 , 应多比较多种方法的优略性，掌握解题方法的本质.
 

【典题4】已知直线\(l：y=kx-2\)，\(M(-2 ,0)\),\(N(-1 ,0)\)，\(O\)为坐标原点，动点\(Q\)满足\(\dfrac{|Q M|}{|Q N|}=\sqrt{2}\)，动点\(Q\)的轨迹为曲线\(C\)
(1)求曲线\(C\)的方程；
(2)若直线\(l\)与圆\(O：x^2+y^2=2\)交于不同的两点\(A\),\(B\)，当\(\angle A O B=\dfrac{\pi}{2}\)时，求\(k\)的值；
(3)若\(k=\dfrac{1}{2}\)，\(P\)是直线\(l\)上的动点，过点\(P\)作曲线\(C\)的两条切线\(PC\)、\(PD\)，切点为\(C\)、\(D\)，探究：直线\(CD\)是否过定点．

【解析】(1)设点\(Q(x ,y)\)，依题意知\(\dfrac{|Q M|}{|Q N|}=\dfrac{\sqrt{(x+2)^{2}+y^{2}}}{\sqrt{(x+1)^{2}+y^{2}}}=\sqrt{2}\)，
整理得\(x^2+y^2=2\)，
\(∴\)曲线\(C\)的方程为\(x^2+y^2=2\).
(2)\(∵\)点\(O\)为圆心，\(\angle A O B=\dfrac{\pi}{2}\)，
\(∴\)点\(O\)到\(l\)的距离\(d=\dfrac{\sqrt{2}}{2} r\)，
\(\therefore \dfrac{2}{\sqrt{k^{2}+1}}=\dfrac{\sqrt{2}}{2} \cdot \sqrt{2} \Rightarrow k=\pm \sqrt{3}\)；
(3)由题意可知：\(O\)、\(P\)、\(C\)、\(D\)四点共圆且在以\(OP\)为直径的圆上，
\({\color{Red}{(对角互补的四边形的四顶点共圆) }}\)

设\(P\left(t, \dfrac{1}{2} t-2\right)\)，则圆心\(\left(\dfrac{t}{2}, \dfrac{t}{4}-1\right)\)，半径\(\sqrt{\dfrac{t^{2}}{4}+\left(\dfrac{t}{4}-1\right)^{2}}\)
得\(\left(x-\dfrac{t}{2}\right)^{2}+\left(y-\dfrac{t}{4}+1\right)^{2}=\dfrac{\mathrm{t}^{2}}{4}+\left(\dfrac{t}{4}-1\right)^{2}\)
即\(x^{2}-t x+y^{2}-\left(\dfrac{1}{2} t-2\right) y=0\)
又\(C\)、\(D\)在圆\(O：x^2+y^2=2\)上
\(\therefore l_{C D}: t x+\left(\dfrac{1}{2} t-2\right) y-2=0\)，即\(\left(x+\dfrac{y}{2}\right) t-2 y-2=0\)，
\({\color{Red}{(直线CD是两圆的公共弦所在直线，故两圆方程相减便得其方程) }}\)
由\(\left\{\begin{array}{l} x+\dfrac{y}{2}=0 \\ 2 y+2=0 \end{array}\right.\)得\(\left\{\begin{array}{l} x=\dfrac{1}{2} \\ y=-1 \end{array}\right.\)，
\(∴\)直线\(CD\)过定点\(\left(\dfrac{1}{2},-1\right)\).
 

巩固练习

1(★★) 求过两条直线\(y=2x+3\)与\(3x-y+2=0\)的交点，且分别满足下列条件的直线方程：
(1)斜率为\(-\dfrac{1}{2}\)；
(2)过点\(P(2 ,3)\)；
(3)平行于直线\(3x+y=1\)．
 

2(★★) 求过直线\(2x+y+4=0\)和圆\((x+1)^{2}+(y-2)^{2}=4\)的交点，并且面积最小的圆的方程．
 
 

3(★★) 求经过圆\(x^2+y^2+8x-6y+21=0\)与直线\(x-y+5=0\)的交点且在\(y\)轴上的弦长为\(2 \sqrt{33}\)的圆的方程．
 
 

4(★★) 求圆心在直线\(x+y=0\)上，且过两圆\(x^2+y^2－2x+10y－24=0\)与\(x^2+y^2+2x+2y-8=0\)的交点的圆的方程．
 
 

5(★★) 过圆\(x^2+y^2=4\)内一点\(A(1 ,1)\)作一弦交圆于\(B\)、\(C\)两点，过点\(B\)、\(C\)作圆的切线\(PB\)、\(PC\)，求点\(P\)的轨迹方程.
 
 

6(★★★) 已知圆\(C\)的圆心在\(x\)轴的正半轴上，半径为\(2\)，且被直线\(l：4x-3y－3=0\)截得的弦长为\(2 \sqrt{3}\)．
(1)圆\(C\)的方程；
(2)设\(P\)是直线\(x+y+4=0\)上动点，过点\(P\)作圆\(C\)的切线\(PA\)，切点为\(A\)，证明：经过\(A\)，\(P\),\(C\)三点的圆必过定点，并求所有定点坐标．
 
 

7(★★★) 如图，已知圆\(M: x^{2}+(y-4)^{2}=4\)，直线\(l\)的方程为\(x-2y=0\)，点\(P\)是直线\(l\)上一动点，过点\(P\)作圆的切线\(PA\)、\(PB\)，切点为\(A\)、\(B\)．
(1)当\(P\)的横坐标为\(\dfrac{16}{5}\)时，求\(∠APB\)的大小；
(2)求证：经过\(A\)、\(P\)、\(M\)三点的圆\(N\)必过定点，并求出所有定点的坐标．

 
 
 
 

8(★★★★) 已知圆\(C\)经过坐标原点\(O\)和点\(G(-2 ,2)\)，且圆心\(C\)在直线\(x+y-2=0\)上．
(1)求圆\(C\)的方程；
(2)设\(PA\)、\(PB\)是圆\(C\)的两条切线，其中\(A\)、\(B\)为切点．
①若点\(P\)在直线\(x-y-2=0\)上运动，求证：直线\(AB\)经过定点；
②若点\(P\)在曲线\(y=\dfrac{1}{4} x^{2}\)(其中\(x>4\))上运动，记直线\(PA\)、\(PB\)与\(x\)轴的交点分别为\(M\)、\(N\)，求\(△PMN\)面积的最小值．
 
 
 
 

参考答案

1.\((1) x+2y-11=0 \quad (2) 2x+y-7=0 \quad (3) 3x+y-8=0\)

2.\(x^{2}+y^{2}+\dfrac{26}{5} x-\dfrac{12}{5} y+\dfrac{37}{5}=0\)

3.\(x^2+y^2-2x+4y-29=0\)或\(x^2+y^2+26x-24y+111=0\)

4.\((x+3)^{2}+(y-3)^{2}=10\)

5.\(x+y=4\)

6.\(\text { (1) }(x-2)^{2}+y^{2}=4\)\((2) (-1 ,-3)\)和\((2 ,0)\)

7.\((1) 60^{\circ}\quad (2) (0,4),\left(\dfrac{8}{5}, \dfrac{4}{5}\right)\)

8.\((1) x^{2}+(y-2)^{2}=4\)；

\((2)\)①直线\(AB\)恒过定点\((1 ,1)\)； ②\(△PMN\)的面积取得最小值\(32\)．