欢迎到学科网下载资料学习【高分突破系列】 高二数学上学期同步知识点剖析精品讲义!
跟贵哥学数学,soeasy!
选择性必修第一册同步提高,难度 3 颗星!
模块导图
知识剖析
1两条直线的交点
设两条直线的方程是 l1∶A1x+B1y+C1=0,l2∶A2x+B2y+C2=0,
两条直线的交点坐标就是方程组 {A1x+B1y+C1=0A2x+B2y+C2=0 的解.
(1) 若方程组有唯一解,则这两条直线相交,此解就是交点的坐标;
(2) 若方程组无解,则两条直线无公共点,此时两条直线平行;
(3) 若方程组有无数个解,则两条直线重合.
2几种距离
(1) 两点距离公式
平面上的两点 P1(x1,y1),P2(x2,y2) 间的距离公式 |P1P2|=√(x2−x1)2+(y2−y1)2.
(2) 点到直线的距离公式
点 P0(x0,y0) 到直线 Ax+By+C=0 的距离 d=|Ax0+By0+C|√A2+B2.
(3) 两平行直线间的距离
两条平行线 Ax+By+C1=0 与 Ax+By+C2=0 间的距离 d=|C1−C2|√A2+B2.
经典例题
【题型一】 直线交点问题
【典题 1】若关于 x、y 的方程组 {x+y=mx+ny=1 有无穷多组解,则 m+n 的值为 –––––.
【解析】关于 x、y 的方程组 {x+y=mx+ny=1 有无穷多组解,
则直线 x+y=m 和直线 x+ny=1 重合,
故 m=1,n=1,所以 m+n=2.
【典题 2】已知直线 kx−y+1=0 和 x−ky=0 相交,且交点在第二象限,则实数 k 的取值范围为 –––––.
【解析】联立方程 {kx−y+1=0x−ky=0,解得 ⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩x=k1−k2y=11−k2, (由于两直线相交,故k≠±1)
因为交点在第二象限,所以 ⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩k1−k2<011−k2>0,解得 -1<k<0,
故实数 k 的取值范围为 (−1,0).
【典题 3】求过直线 x+2y+1=0 与直线 2x−y+1=0 的交点且在两坐标轴上截距相等的直线方程.
【解析】方法1(求出交点,再用截距式求解)
由 {x+2y+1=02x−y+1=0 得交点坐标 P(−35,−15),
由于直线在两坐标轴上截距相等, (截距相等要注意是否为0)
(i) 当截距为 0,此时直线方程为 y=kx,代入点 P 得 k=13,
即所求直线方程为 x−3y=0.
(ii) 当截距不等于 0,设直线方程为 xa+ya=1,代入点 P 得 a=−45,
此时所求直线方程为 5x+5y+4=0,
综上所述,所求直线方程为 x−3y=0 或 5x+5y+4=0.
方法2 设所求直线方程为 x+2y+1+λ(2x−y+1)=0,
(i) 当直线过原点时,则 1+λ=0,则 λ=−1,
此时所求直线方程为 x−3y=0.
(ii) 当直线不过原点时,令 x=0,解得 y=λ+1λ−2,令 y=0,解得 x=−λ+12λ+1,
由题意得 λ+1λ−2=−λ+12λ+1,解得 λ=13,此时所求直线方程为 5x+5y+4=0,
(∗) 中不包括直线 2x−y+1=0,而它显然不满足题意,
综上所述,所求直线方程为 x−3y=0 或 5x+5y+4=0.
【点拨】本题中方法 2 采取了直线系方程的方法.
过两条已知直线 l1:A1x+B1y+C1=0 和 l2:A2x+B2y+C2=0 交点的直线系方程 A1x+B1y+C1+λ(A2x+B2y+C2)=0
(λ∈R, 这个直线系下不包括直线 l2:A2x+B2y+C2=0,解题时注意检验 l2 是否满足题意)
【典题 4】若 k>4,直线 kx−2y−2k+8=0 与 2x+k2y−4k2−4=0 和坐标轴围成的四边形面积的取值范围是 –––––.
【解析】(确定所求的四边形面积,要四边形的图象,即了解两条直线与坐标轴的交点与两直线的交点)
由 {kx−2y−2k+8=02x+k2y−4k2−4=0 得 {x=2y=4,即两直线的交点为定点 B(2,4),
而直线 L:kx−2y−2k+8=0 与 x 轴的交点 A(2−8k,0),与 y 轴的交点 D(0,4−k),
直线 M:2x+k2y−4k2−4=0 与 x 轴的交点 E(2k2+2,0),与 y 轴的交点 C(0,4+4k2),
(由k>4,很容易确定各点的位置)
如图所示,
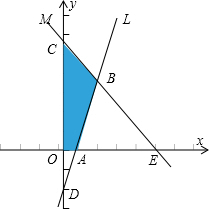
∴S四边形OABC=S△OCE−S△ABE
=12×(4+4k2)(2k2+2)−12×4×(2k2+2−2+8k)
=4k2−16k+8=4(1k−2)2−8,
∵k>4,∴0<1k<14,
则 174<S<8,
故 k>4 时,所求面积的取值范围是 (174,8).
【点拨】
① 根据题意画出正确的图象是正确求解的基础,对于含参的直线,要注意它是否存在定点、斜率的正负、与 x、y 轴交点的位置等.
② 而定点如何确定,如直线 M:2x+k2y−4k2−4=0 变式为 k2(y−4)+(2x−4)=0 易得过定点 B(2,4).
巩固练习
1(★) 曲线 y=|x| 与 y=kx+1 的交点的情况是 ( )
A.最多有两个交点 B.两个交点 C.一个交点 D.无交点
2(★) 关于 x、y 的二元一次方程组 {mx+y=−13mx−my=2m+3 无解,则 m= –––––.
3(★) 若三条直线 2x+3y+8=0,x−y−1=0 和 x+ky=0 交于一点,则 k 的值为 –––––.
4(★★) 直线 kx−y−1=0 与直线 x+2y−2=0 的交点在第四象限,则实数 k 的取值范围为 –––––.
5(★★★) 在平面直角坐标系 xOy 中,已知点 A(1,2),点 M(4,2),点 N 在线段 OA 的延长线上.设直线 MN 与直线 OA 及 x 轴围成的三角形面积为 S,则 S 的最小值为 –––––.
参考答案
1.A
2.0
3.−12
4.(−12,12)
5.12
【题型二】 距离问题
情况1 两点间的距离
【典题 1】在平面直角坐标系内,到点 A(1,2),B(1,5),C(3,6),D(7,−1) 的距离之和最小的点的坐标是 –––––.
【解析】如图,设平面直角坐标系中任一点 P,

P 到点 A(1,2),B(1,5),C(3,6),D(7,−1) 的距离之和为:
PA+PB+PC+PD=PB+PD+PA+PC≥BD+AC=QA+QB+QC+QD,
故四边形 ABCD 对角线的交点 Q 即为所求距离之和最小的点.
∵A(1,2),B(1,5),C(3,6),D(7,−1),
∴AC,BD 的方程分别为 y−26−2=x−13−1,y−5−1−5=x−17−1,
即 2x−y=0,x+y−6=0.
解方程组 {2x−y=0x+y−6=0 得 Q(2,4).
【点拨】本题是从几何方法入手,利用 “一点到两定点距离之和最小值为两定点距离” 的三点共线最值模型求解.
【典题 2】设 a,b∈R,√(a−1)2+(b−1)2+√(a+1)2+(b+1)2 的最小值为 –––––.
【解析】从几何意义看,
√(a−1)2+(b−1)2+√(a+1)2+(b+1)2 表示点 (a,b) 到点 (1,1) 和 (−1,−1) 距离的和,
其最小值为 (1,1) 和 (−1,−1) 两点间的距离 2√2.
【点拨】本题是函数最值问题,但很巧妙的使用了两点距离公式从而化为几何最值问题。平面上的两点 P1(x1,y1),P2(x2,y2) 间的距离 |P1P2|=√(x2−x1)2+(y2−y1)2,若给两点坐标我们用此公式很容易得到两点距离,若给了 √(a−1)2+(b−1)2 能够联想到两点距离公式呢?这里就提醒我们在掌握知识的 “直用” 也要会 “逆用”.
【典题 3】已知 m∈R,动直线 l1:x+my−2=0 过定点 A,动直线 l2:mx−y−2m+3=0 过定点 B,若 l1 与 l2 交于点 P(异于点 A,B),则 |PA|+|PB| 的最大值为 –––––.
【解析】l1:x+my−2=0 可变形为 (x−2)+my=0,过定点 A(2,0),
l2:mx−y−2m+3=0 可变形为 m(x−2)−(y−3)=0,过定点 B(2,3),

方法1代数法
由 {x+my−2=0mx−y−2m+3=0 可得交点 P(2−3mm2+1,3m2+1),
则 |PA|=√(3mm2+1)2+(3m2+1)2=3√m2+1,|PB|=√(3mm2+1)2+(3m2+1−3)2=3√2|m|m2+1
设 a=3√m2+1,b=3√2|m|m2+1,则 a2+b2=9, (发现这关系是关键)
则 (a+b2)2≤a2+b22=92⇒a+b≤3√2,当 a=b=3√22 时取到等号,
即 |PA|+|PB| 的最大值为 3√2,当 m=±1 时取到最值.
方法2几何法
观察直线斜率可知直线 l1 与直线 l2 垂直, (发现这一隐含条件是关键)
则有 PA⊥PB,且 |PA|2+|PB|2=|AB|2=9,
(相当于方法1的a2+b2=9,此时题目转化为“已知|PA|2+|PB|2=9,求|PA|+|PB|的最大值”,想到基本不等式)
由 |PA|2+|PB|2≥2|PA|⋅|PB|⇒|PA|⋅|PB|≤92
所以 (|PA|+|PB|)2=|PA|2+|PB|2+2|PA|⋅|PB|≤18,
即 |PA|+|PB|≤3√2,当且仅当 |PA|=|PB| 时取等号,
所以 |PA|+|PB| 的最大值为 3√2.
【思考】体会下两种方法的异同与优劣性,方法 1 中 |PA|+|PB|=3√m2+1+3√2|m|m2+1 还能转化为函数最值求解么?
【典题 4】已知点 A(4,0),B(0,2),对于直线 l:x−y+m=0 的任意一点 P,都有 |PA|2+|PB|2>18,则实数 m 的取值范围是 –––––.
【解析】根据题意,点 P 在直线 l:x−y+m=0 上,设 P 的坐标为 (x,x+m),
则有 |PA|2+|PB|2
=(x−4)2+(x+m−0)2+(x−0)2+(x+m−2)2
=4x2+(4m−12)x+(2m2−4m+20),
若对于直线 l:x−y+m=0 上的任意一点 P,都有 |PA|2+|PB|2>18,
则 4x2+(4m−12)x+(2m2−4m+20)>18 恒成立,
即 4x2+(4m−12)x+(2m2−4m+2)>0 对于 R 恒成立,
则有 △=(4m−12)2-16(2m2−4m+2)<0,即 m2+2m−7>0,
解可得 m>−1+2√2 或 m<−1−2√2,
即 m 的取值范围为 (−∞,−1−2√2)∪(−1+2√2,+∞).
【点拨】本题采取设元的方法,把 |PA|2+|PB|2>18 转化为恒成立问题处理。这是典型的代数方法,又是否存在几何的思路呢?
情况2 点到直线的距离
【典题 1】已知曲线 C:xy=27 和直线 l:3x+4y=0,点 M 在曲线 C 上,点 N 在直线 l 上,则 |MN| 的最小值是 –––––.
【解析】设点 M(a,b),则 ab=27,|MN| 取到最小值时是点 M 到直线 l 的距离,
点 M 到直线 l 的距离为 d=|3a+4b|5,
∴d2=9a2+16b2+24ab25≥24ab+24ab25=48×2725⇒d≥365,
∴|MN| 的最小值是 365.
【典题 2】已知直线 l 方程为 (2+m)x+(1−2m)y+4−3m=0.那 m 为何值时,点 Q(3,4) 到直线的距离最大,最大值为多少?
【解析】方法一函数法
点 Q 到直线 l 的距离 d=3(2+m)+4(1−2m)+4−3m√(2+m)2+(1−2m)2=14−8m√5(m2+1),
则 d2=45⋅(7−4m)2m2+1=45⋅16m2−56m+49m2+1=45⋅(16+−56m+33m2+1)
令 t=−56m+33,
则 −56m+33m2+1=3136tt2−66t+4225=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩0,t=03136t+4225t−66,t≠0,
由对勾函数易得 t+4225t−66≥64(当 t=65 时取到等号),t+4225t−66≤−196,
则 0≤3136tt2−66t+4225≤49 或 −3136196<3136tt2−66t+4225<0
故当 t=65,即 m=−47 时,d2 取到最大值 45⋅(16+49)=52,即 dmax=2√13.
方法二几何法
直线 (2+m)x+(1−2m)y+4−3m=0 化为 (x−2y−3)m=−2x−y−4.
由 {x−2y−3=0−2x−y−4=0,得 {x=−1y=−2,
∴ 直线必过定点 (−1,−2).
当点 Q(3,4) 到直线的距离最大时,QP 垂直于已知的直线,
即点 Q 与定点 P(−1,−2) 的连线就是所求最大值,
此时直线 PQ 与直线 (2+m)x+(1−2m)y+4−3m=0 垂直,
∵kPQ=−2−4−1−3=32,∴2+m2m−1=−23,解得 m=−47,
此时,点 Q(3,4) 到直线的最大距离是 √(3+1)2+(4+2)2=2√13.
综上所述,m=−47 时,点 Q(3,4) 到直线的距离最大,最大值为 2√13.
【点拨】体会下两种方法的优劣性.
【典题 3】设直线 l1:y=k1x+1,l2:y=k2x−1, 其中实数 k1,k2 满足 k1k2+1=0.
(1) 证明:直线 l1 与 l2 相交;
(2) 试用解析几何的方法证明:直线 l1 与 l2 的交点到原点距离为定值;
(3) 设原点到 l1 与 l2 的距离分别为 d1 和 d2,求 d1+d2 的最大值.
【解析】证明:(1) (只需证明k1≠k2)
反证法:假设 l1 与 l2 不相交,(若从正面入手较难,可考虑“反证法”)
则 l1 与 l2 平行,有 k1=k2,
代入 k1k2+1=0,得 k21+1=0,
这与 k1 为实数的事实相矛盾,∴k1≠k2,故 l1 与 l2 相交.
(2) 由 (1) 知 k1≠k2,由方程组 {y=k1x+1y=k2x−1
解得交点 P 的坐标 (x,y) 为 ⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩x=2k2−k1y=k2+k1k2−k1,
而 x2+y2=(2k2−k1)2+(k2+k1k2−k1)2=4+k22+k21+2k1k2k22+k21−2k1k2=k21+k22+2k21+k22+2=1.
即 l1 与 l2 的交点到原点距离为 1.
(3)d1+d2=1√1+k21+1√1+k22
(从函数的角度思考,遇到二元,要不基本不等式,要不消元)
=1√1+k21+1√1+1k21=1√1+k21+|k1|√1+k21
=1+|k1|√1+k21(遇到根号,基本思路是考虑平方,换元)
=√(1+|k1|)21+k21
(遇到y=a1x2+b1x+c1a2x2+b2x+c2形式,利用分离常数法、基本不等式)
=√1+2|k1|1+k21=
⎷1+21|k1|+|k1|≤√2,
当 |k1|=1 即 k1=±1 时,d1+d2 的最大值是 √2.
【点拨】对于一些常见的式子 (或模型) 的处理手段要掌握好,这是基本功.
情况3 两平行线间的距离
【典题 1】若平面内两条平行线 l1:x+(a−1)y+2=0,l2:ax+2y+1=0 间的距离为 3√55,则实数 a= –––––.
【解析】∵ 平面内两条平行线 l1:x+(a−1)y+2=0,l2:ax+2y+1=0,
∴1a=a−12≠21,∴a=2 或 a=−1.
当 a=2 时,两条平行直线即 l1:2x+2y+4=0,l2:2x+2y+1=0,
它们之间的距离为 |4−1|√4+4=32√2,不满足条件.
当 a=−1 时,两条平行直线即 l1:x−2y+2=0,l2:x−2y−1=0,
它们之间的距离为 |2+1|√1+4=3√55,满足条件,
故实数 a=−1.
【点拨】用两平行直线距离公式时,要确定 x、y 前的系数一致后才能使用.
【典题 2】正方形 ABCD 一条边 AB 所在方程为 x+3y−5=0,另一边 CD 所在直线方程为 x+3y+7=0,
(1) 求正方形中心 G 所在的直线方程;
(2) 设正方形中心 G(x0,y0),当正方形仅有两个顶点在第一象限时,求 x0 的取值范围.
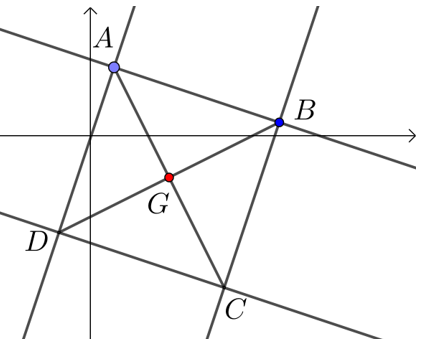
【解析】(1) 由于正方形中心 G 所在直线平行于直线 x+3y−5=0,
设中心所在直线为 x+3y+c=0,
由平行线间的距离公式得 |c+5|√12+32=|c−7|√12+32,解得 c=1.
则正方形中心 G 所在的直线方程为 x+3y+1=0;
(2) 正方形的边长即为平行直线 AB 与 CD 间的距离 d=|7+5|√12+32=12√10,
设正方形 BC 所在直线方程为 3x−y+m=0, (用到了正方形内角是直角的性质)
由于中心 G(x0,y0) 到 BC 的距离均等于 d2=6√10, (相当用到了正方形四边相等的性质)
那么 |3x0−y0+m|√12+32=6√10,解得 m=±6−3x0+y0①,
又因为 G 在直线 x+3y+1=0 上,那么 x0+3y0+1=0,即 y0=−x0+13②,
把②代入①得 m=±6−10x0+13③,
联立方程 {x+3y−5=03x−y+m=0,解得 ⎧⎪
⎪⎨⎪
⎪⎩x=−3m+510y=m+1510,
由于正方形只有两个点在第一象限,
那么 {x>0y>0,,就是 ⎧⎪
⎪⎨⎪
⎪⎩−3m+510>0m+1510>0,解得 −15<m<53④,
把③代入④得到 −15<±6−10x0+13<53,解得 65<x0<135.
故 x0 的取值范围为 (65,135).
【点拨】结合图象,充分利用图象的性质得到变量的限制要求,从而求出变量范围.
巩固练习
1(★) 已知 △ABC 的顶点为 A(2,1),B(−2,3),C(0,−1),则 AC 边上的中线长为 –––––.
2(★) 点 P(cosθ,sinθ) 到直线 3x+4y−12=0 的距离的取值范围为 –––––.
3(★) 到直线 3x-4y+1=0 的距离为 3 且与此直线平行的直线方程是 –––––.
4(★★) 两条平行线 l1,l2 分别过点 P(−1,2),Q(2,−3),它们分别绕 P,Q 旋转,但始终保持平行,则 l1,l2 之间距离的取值范围是 –––––.
5(★) 已知直线 l 经过点 P(5,10),且原点到它的距离为 5,则直 线l 的方程为 –––––.
6(★★) 已知点 M(a,b) 在直线 l:3x+4y=25 上,则 √a2+b2 的最小值为 –––––.
7(★★) 若直线 m 被两平行线 l1:x−√3y+1=0 与 l2:x−√3y+3=0 所截得的线段的长为 1,则直线 m 的倾斜角的大小为 –––––.
8(★★) 已知实数 a,b,c 成等差数列,则点 P(2,−1) 到直线 ax+by+c=0 的最大距离是 –––––.
9(★★) 平面直角坐标系内,动点 P(a,b) 到直线 l1:y=12x 和 l2:y=−2x 的距离之和是 4,则 a2+b2 的最小值是 –––––.
10(★★★) 在平面直角坐标系 xOy 中,设定点 A(a,a),P 是函数 y=1x(x>0) 图象上一动点.若点 P,A 之间的最短距离为 2√2,则满足条件的实数 a 的所有值为 –––––.
11(★★★) 已知点 P,Q 分别在直线 l1:x+y+2=0 与直线 l2:x+y−1=0 上,且 PQ⊥l1,点 A(−3,−3),B(32,12),则 |AP|+|PQ|+|QB| 的最小值为 –––––.
参考答案
1.3√2
2.[75,175]
3.3x-4y+16=0 或 3x-4y-14=0
4.(0,√34]
5.x=5 或 3x−4y+25=0
6.5
7.120°
8.√2
9.8
10.a=√10 或 a=−1
11.√13+3√22









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)