2.2 直线的位置关系

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

选择性必修第一册同步拔高，难度3颗星！

模块导图

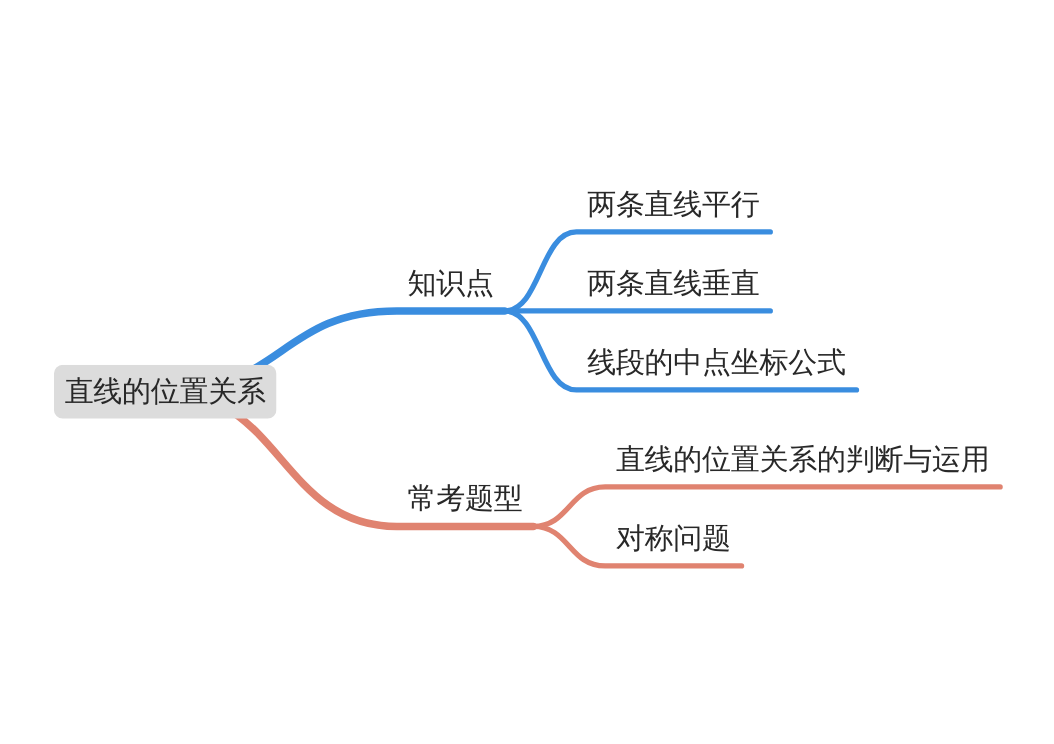
知识剖析

1两直线的位置关系

\({\color{Red}{解释}}\)
对于两条不重合的直线\(l_1\),\(l_2\)，其斜率存在时分别为\(k_1\),\(k_2\)，
则有\(l_1 // l_2 ⇔k_1=k_2\)或\(l_1\),\(l_2\)的斜率都不存在.
有\(l_1⊥ l_2⇔k_1⋅ k_2=-1\)或\(k_1=0\)且\(l_2\)的斜率不存在或\(k_2=0\)且\(l_1\)的斜率不存在.
 

2 线段的中点坐标公式

若点\(P_1\),\(P_2\)的坐标分别是\((x_1 ,y_1)\),\((x_2 ,y_2)\), 则线段\(P_1 P_2\)中点坐标为\(M\left(\dfrac{x_{1}+x_{2}}{2}, \dfrac{y_{1}+y_{2}}{2}\right)\).
 

3 常见的直线系方程

平行于直线\(Ax+By+C=0\)的直线系方程\(Ax+By+C_0=0(C≠C_0)\)；
垂直于于直线\(Ax+By+C=0\)的直线系方程\(Bx-Ay+C_0=0\)；
过两条已知直线\(l_1:A_1 x+B_1 y+C_1=0\)和\(l_2:A_2 x+B_2 y+C_2=0\)交点的直线系方程
\(A_1 x+B_1 y+C_1+λ(A_2 x+B_2 y+C_2 )=0\)；
(\(λ∈R\), 这个直线系下不包括直线\(l_2:A_2 x+B_2 y+C_2=0\)，解题时注意检验\(l_2\)是否满足题意)
 

4 对称性问题

(1)点关于点的对称
点\(P(x_0 ,y_0)\)关于\(A(a ,b)\)的对称点为\(P'(2a-x_0 ,2b-y_0)\)；
 

(2)点关于直线的对称
设点\(P(x_0 ,y_0)\)关于直线\(l：y=kx+b\)的对称点为\(P'(x' ,y')\)
则有\(\left\{\begin{array}{c} \dfrac{y^{\prime}-y_{0}}{x^{\prime}-x_{0}} \cdot k=-1 \\ \dfrac{y^{\prime}+y_{0}}{2}=k \cdot \dfrac{x^{\prime}+x_{0}}{2}+b \end{array}\right.\)可求出\(x'\),\(y'\)，从而得到点\(P'\).

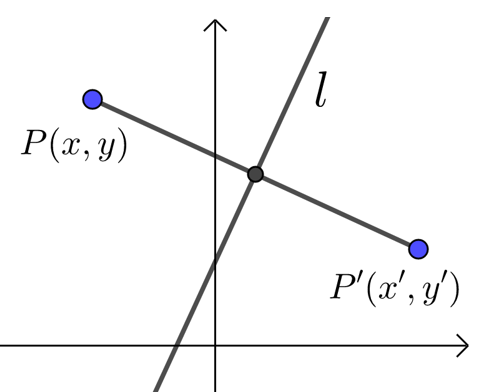
(直线\(l\)是线段\(PP'\)的垂直平分线，则\(k_{P P^{\prime}} \cdot k=-1\)，\(PP'\)的中点\(\left(\dfrac{x^{\prime}+x_{0}}{2}, \dfrac{y^{\prime}+y_{0}}{2}\right)\)在直线\(l\)上)
 

(3)直线关于直线的对称
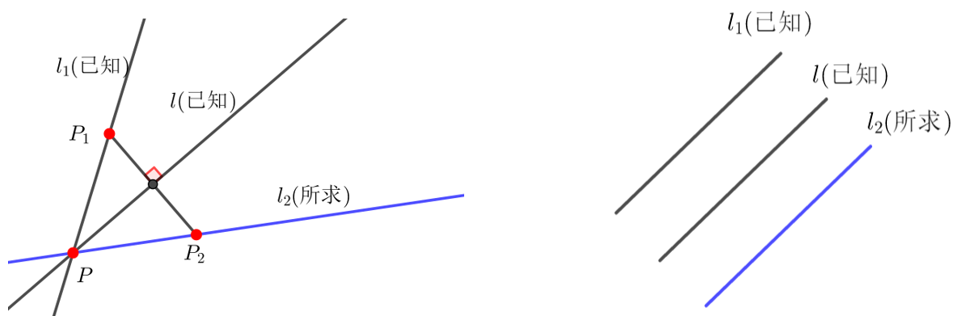
\((i)\)若已知直线\(l_1\)与对称轴\(l\)相交于点\(P\)，则与\(l_1\)对称的直线\(l_2\)过点\(P\)，再求出直线\(l_1\)上一点\(P_1\)关于对称轴\(l\)的对称点\(P_2\)，则由点\(P\)与\(P_2\)可求出直线\(l_2\)的方程；
\((ii)\)若已知直线\(l_1\)与对称轴\(l\)平行，求与已知直线\(l_1\)关于对称轴\(l\)对称的直线\(l_2\)，利用直线\(l_1\)、\(l_2\)到直线\(l\)的距离相等便可求.(方法其实多样，大致均可转化为点关于直线对称问题)

 

经典例题

【题型一】 直线的位置关系的判断

【典题1】已知\(l_1：x+my+6=0\)，\(l_2：(m-2)x+3y+2m=0\)，分别求\(m\)的值，使得\(l_1\)和\(l_2\)：\((1)\)垂直；\((2)\)平行；\((3)\)重合；\((4)\)相交．
【解析】(1)若\(l_1\)和\(l_2\)垂直，
\({\color{Red}{方法1 }}\)把直线化为斜截式，由斜率\(k_1\cdot k_2=-1\)求解
当\(m=0\)时，\(l_1:x=-6\)，\(l_2:-2x+3y=0\)，显然不满足题意；
\({\color{Red}{ (注意斜率不存在的情况)}}\)
当\(m≠0\)时，\(k_{1}=-\dfrac{1}{m}\)，\(k_{2}=\dfrac{m-2}{3}\)，则\(-\dfrac{1}{m} \cdot \dfrac{m-2}{3}=-1\)，解得\(m=\dfrac{1}{2}\)；
\({\color{Red}{方法2 }}\)从一般式来看，可得\(1\cdot (m-2)+3\cdot m=0\)，\(\therefore m=\dfrac{1}{2}\)；
(2)若\(l_1\)和\(l_2\)平行，则\(\dfrac{m-2}{1}=\dfrac{3}{m} \neq \dfrac{2 m}{6}\)， \({\color{Red}{ (也可如(1)化为斜截式求解)}}\)
\(\therefore\left\{\begin{array}{l} m^{2}-2 m-3=0 \\ m \neq \pm 3 \end{array}\right.\)解得\(m=-1\)，
(3)若\(l_1\)和\(l_2\)重合，则\(\dfrac{m-2}{1}=\dfrac{3}{m}=\dfrac{2 m}{6}\)，\(∴m=3\)，
(4)若\(l_1\)和\(l_2\)相交，则由(2)(3)可知\(m≠3\)且\(m≠-1\).
【点拨】 判定直线的位置，有斜截式和一般式两种角度；由斜截式判定时，要注意直线斜率是否存在；由一般式判定时，切记不要死记结论.
 

【典题2】顺次连接\(A(-4 ,3)\)、\(B(2 ,5)\)、\(C(6 ,3)\)、\(D(-3 ,0)\)，所组成的图形是(　　)
A．平行四边形 \(\qquad \qquad\) B．直角梯形 \(\qquad \qquad\) C．等腰梯形 \(\qquad \qquad\) D．以上都不对
【解析】\({\color{Red}{(要判断四边形形状，需要判断各边的位置关系，可从直线斜率入手) }}\)
\(AB\)的斜率为\(\dfrac{5-3}{2+4}=\dfrac{1}{3}\)，\(CD\)的斜率为\(\dfrac{3-0}{6+3}=\dfrac{1}{3}\)，
则\(k_{A B}=k_{C D}\)，故\(AB||CD\)；
由\(AD\)的斜率为\(\dfrac{3-0}{-4+3}=-3\)得\(k_{A D} \cdot k_{A B}=-1\)，则\(AB⊥AD\)；
由\(BC\)的斜率为\(\dfrac{5-3}{2-6}=-\dfrac{1}{2}\)得\(k_{A D} \neq k_{B C}\)，则\(AD\)与\(BC\)不平行，
故四边形为直角梯形，故选\(B\)．
 

【典题3】已知\(|m|<1\)，直线\(l_1：y=mx+1\)，\(l_2：x=-my+1\)，\(l_1\)与\(l_2\)相交于点\(P\)，\(l_1\)交\(y\)轴于点\(A\)，\(l_2\)交\(x\)轴于点\(B\)
(1)证明：\(l_1⊥l_2\)；
(2)用\(m\)表示四边形\(OAPB\)的面积\(S\)，并求出\(S\)的最大值.
【解析】(1)当\(m=0\)时，直线\(l_1：y=1\)，\(l_2：x=1\)，显然有\(l_1⊥l_2\)；
\({\color{Red}{ (确定l_2是否一定存在斜率) }}\)
当\(m≠0\)时，\(l_1\)与\(l_2\)的斜率分别为\(m\)，\(\dfrac{1}{-m}\)，斜率之积\(m \cdot \dfrac{1}{-m}=-1\)，故\(l_1⊥l_2\)．
综上，\(l_1⊥l_2\).
(2)由题意知，\(A(0 ,1)\)，\(B(1 ,0)\)，

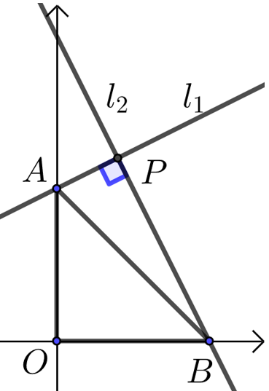
由\(l_1\)与\(l_2\)相的方程联立方程组\(\left\{\begin{array}{c} y=m x+1 \\ x=-m y+1 \end{array}\right.\)，
解得点\(P\left(\dfrac{1-m}{1+m^{2}}, \dfrac{1+m}{1+m^{2}}\right)\)，
因\(|m|<1\)，故点\(P\)在第一象限，
\({\color{Red}{ (注意这点，否则图不准确，导致四边形OAPB判断出错) }}\)
则\(|P A|=\sqrt{\left(\dfrac{1-m}{1+m^{2}}\right)^{2}+\left(\dfrac{1+m}{1+m^{2}}-1\right)^{2}}=\dfrac{1-m}{\sqrt{1+m^{2}}}\)，
\(|P B|=\sqrt{\left(\dfrac{1-m}{1+m^{2}}-1\right)^{2}+\left(\dfrac{1+m}{1+m^{2}}\right)^{2}}=\dfrac{1+m}{\sqrt{1+m^{2}}}\)，
由(1)可知\(PA⊥PB\)，
\(\therefore S_{\triangle A P B}=\dfrac{1}{2}|P A| \cdot|P B|=\dfrac{1-m^{2}}{2\left(1+m^{2}\right)}\)，
\(\therefore S_{\text {四边形 } O A P B}=S_{O A B}+S_{\triangle A P B}=\dfrac{1}{2}+\dfrac{1-m^{2}}{2\left(1+m^{2}\right)}=\dfrac{1}{1+m^{2}}\)，
故\(m=0\)时，\(S\)有最大值为\(1\)．
【点拨】 谨记\(l_1 // l_2 ⇔k_1=k_2\)，\(l_1⊥ l_2⇔k_1⋅ k_2=-1\)成立的前提是直线斜率\(k_1\),\(k_2\)存在，若不确定要分类讨论.
 

巩固练习

1(★)若\(l_1\)与\(l_2\)为两条不重合的直线，它们的倾斜角分别为\(a_1\),\(a_2\)，斜率分别为\(k_1\),\(k_2\)，则下列命题
(1)若\(l_1∥l_2\)，则斜率\(k_1=k_2\)；
(2)若斜率\(k_1=k_2\)，则\(l_1∥l_2\)；
(3)若\(l_1∥l_2\)，则倾斜角\(a_1=a_2\)；
(4)若倾斜角\(a_1=a_2\)，则\(l_1∥l_2\)；
其中正确命题的个数是 \(\underline{\quad \quad}\) .
 

2(★)已知直线\(l_1：x+2ay-1=0\)，与\(l_2：(2a-1)x-ay-1=0\)平行，则\(a\)的值是\(\underline{\quad \quad}\) .
 

3(★)三条直线\(l_1：x-y=0\),\(l_2：x+y-2=0\)，\(l_3：5x-ky-15=0\)构成一个三角形，则\(k\)的取值范围是\(\underline{\quad \quad}\) .
 

4(★)已知直线\(l_1：mx+4y-2=0\)与\(l_2：2x-5y+n=0\)互相垂直，其垂足为\((1 ,p)\)，则\(m+n-p\)的值为\(\underline{\quad \quad}\) .
 

5(★)直线\(l\)过点\(A(3 ,4)\)且与点\(B(-3 ,2)\)的距离最远，那么\(l\)的方程为\(\underline{\quad \quad}\) .
 

6(★★)[多选题] 已知等腰直角三角形\(ABC\)的直角顶点为\(C(3 ,3)\)，点\(A\)的坐标为\((0 ,4)\)，则点\(B\)的坐标为(　　)
A．\((2 ,0)\) \(\qquad \qquad \qquad \qquad\) B．\((6 ,4)\)\(\qquad \qquad \qquad \qquad\) C．\((4 ,6)\) \(\qquad \qquad \qquad \qquad\) D．\((0 ,2)\)
 

7(★★★)在\(△ABC\)中，已知\(M(1 ,6)\)是\(BC\)边上一点，边\(AB\),\(AC\)所在直线的方程分别为\(2x-y+7=0\),\(x-y+6=0\)．
(1)若\(AM⊥BC\)，求直线\(BC\)的方程；
(2)若\(|BM|=|CM|\)，求直线\(BC\)在\(x\)轴上的截距．
 
 

参考答案

1.\(4\)
2.\(0\)或\(\dfrac{1}{4}\)
3.\(k∈R\)且\(k≠±5\),\(k≠-10\)
4.\(0\)
5.\(3x+y-13=0\)
6.\(AC\)
7.\((1) 2x+y-8=0\)\(\text { (2) } \dfrac{19}{5}\)
 

【题型二】对称问题

【典题1】已知直线\(y=2x\)是\(△ABC\)中\(∠C\)的平分线所在的直线，若点\(A\)、\(B\)的坐标分别是\((-4 ,2)\)，\((3 ,1)\)，则点\(C\)的坐标为\(\underline{\quad \quad}\) .
【解析】
\({\color{Red}{(直线y=2x是角平分线，意味直线AC与BC关于y=2x对称) }}\)

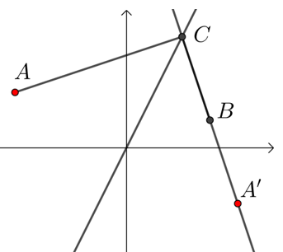
设\(A(-4 ,2)\)关于直线\(y=2x\)的对称点为\(A'(x ,y)\)，
则\(\left\{\begin{array}{l} \dfrac{y-2}{x+4} \times 2=-1 \\ \dfrac{y+2}{2}=2 \times \dfrac{-4+x}{2} \end{array}\right.\)\((*)\)，解得\(\left\{\begin{array}{l} x=4 \\ y=-2 \end{array}\right.\)，即\(A'(4 ,-2)\)．
\({\color{Red}{(这是点关于直线对称的问题，理解到直线y=2x是AA'的垂直平分线易得(*)式)}}\)
\(∴\)直线\(BA'\)方程为\(y-1=\dfrac{-2-1}{4-3}(x-3)=-3(x-3)\)，
化为\(3x+y-10=0\)． \({\color{Red}{(点A'在直线BC上) }}\)
联立\(\left\{\begin{array}{l} 3 x+y-10=0 \\ y=2 x \end{array}\right.\)，解得\(\left\{\begin{array}{l} x=2 \\ y=4 \end{array}\right.\)，可得\(C(2 ,4)\)．
(对称轴\(y=2x\)与直线\(BC\)的交点就是点\(C\))
【点拨】 建议通过画图去理解它们之间的关系，在图中你能更容易发现一些隐含信息.
 

【典题2】如图已知\(A(4 ,0)\)、\(B(0 ,4)\)、\(O(0 ,0)\)，若光线\(L\)从点\(P(2 ,0)\)射出，直线\(AB\)反射后到直线\(OB\)上，在经直线\(OB\)反射回原点\(P\)，则光线\(L\)所在的直线方程为\(\underline{\quad \quad}\) .

【解析】由题意知直线\(AB\)的方程为\(y=-x+4\)，

设光线分别射在\(AB\)、\(OB\)上的\(M、N\)处，
\({\color{Red}{ (本题就是求直线PM方程，只要求出点M便可)}}\)
由于光线从点\(P\)经两次反射后又回到\(P\)点，
根据反射规律，则\(∠PMA=∠BMN\)，\(∠PNO=∠BNM\)．
\({\color{Red}{(反射问题，当然想到入射角相等，数学上是对称问题) }}\)
作出点\(P\)关于\(OB\)的对称点\(P_1\)，作出点\(P\)关于\(AB\)的对称点\(P_2\)，
则\(∠P_2 MA=∠PMA=∠BMN\)，\(∠P_1 NO=∠PNO=∠BNM\)，
\(∴P_1\),\(N\),\(M\),\(P_2\)共线， \({\color{Red}{(通过平几知识得到四点共线) }}\)
易得点\(P\)关于\(y\)轴的对称点\(P_1 (-2 ,0)\)，
\(∵OA=OB=4\),\(∴∠P_2 AB=∠PAB=45°\)，
\(∴P_2 A⊥OA\)，\(∴P_2\)的横坐标为\(4\)，
由对称性可知\(P_2 A=PA=2\)，可得\(P_2\)的纵坐标为\(2\)，
\(∴P_2 (4 ,2)\)，
\({\color{Red}{ (求P_2的坐标常规方法是点关于直线对称的套路，但有时通过细致的观察，不走寻常路更容易得到你想要的，}}\)
\({\color{Red}{ 要善于思考、观察)}}\)
\(∴\)直线\(PP_2\)方程\(\dfrac{y}{x+2}=\dfrac{2}{4+2}\)，即\(x-3y+2=0\)，
联立\(\left\{\begin{array}{l} x-3 y+2=0 \\ x+y-4=0 \end{array}\right.\)，得\(x=\dfrac{5}{2}\)，\(y=\dfrac{3}{2}\)，则\(M\left(\dfrac{5}{2}, \dfrac{3}{2}\right)\)，
\(∴\)直线\(P M: \dfrac{y}{x-2}=\dfrac{\dfrac{3}{2}}{\dfrac{5}{2}-2}\)，
即光线\(L\)所在的直线方程为\(y=3x-6\)．
【点拨】 反射问题的本质还是对称问题，平时处理一类问题中在掌握通法的同时也要注意“巧法”，根据题目的特殊性多思考与观察！
 

【典题3】已知\(O\)为坐标原点，倾斜角为\(\dfrac{2 \pi}{3}\)的直线\(l\)与\(x\),\(y\)轴的正半轴分别相交于点\(A\),\(B\)，\(△AOB\)的面积为\(8 \sqrt{3}\)．
(1)求直线\(l\)的方程；
(2)直线\(l^{\prime}: y=-\dfrac{\sqrt{3}}{3} x\)，点\(P\)在\(l'\)上，求\(|PA|+|PB|\)的最小值．
【解析】(1)由题意可得：直线\(l\)的斜率\(k=\tan \dfrac{2 \pi}{3}=-\sqrt{3}\)，
设直线\(l\)的方程为\(y=-\sqrt{3} x+b\)．
可得直线\(l\)与坐标轴的正半轴交点为\(A\left(\dfrac{\sqrt{3}}{3} b, 0\right)\),\(B(0 ,b)\)，其中\(b>0\)．
\(\therefore S_{\triangle O A B}=\dfrac{1}{2} \times \dfrac{\sqrt{3}}{3} b \times b=8 \sqrt{3}\)，解得\(b=4 \sqrt{3}\)，
\(∴\)直线\(l\)的方程为\(y=-\sqrt{3} x+4 \sqrt{3}\)．
(2)由(1)可得\(A(4 ,0)\)，\(B(0,4 \sqrt{3})\)，

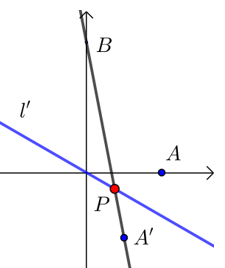
\({\color{Red}{ (求|PA|+|PB|的最小值是“将军饮马”问题，则要求点A或B关于直线l'的对称点)}}\)
设点\(A\)关于直线\(l'\)的对称点\(A'(m ,n)\)，
则\(\left\{\begin{array}{l} \dfrac{n-0}{m-4}=\sqrt{3} \\ \dfrac{n}{2}=-\dfrac{\sqrt{3}}{3} \cdot \dfrac{m+4}{2} \end{array}\right.\)，解得\(\left\{\begin{array}{l} m=2 \\ n=2 \sqrt{3}-4 \end{array}\right.\)，
\(\therefore A^{\prime}(2,2 \sqrt{3}-4)\)．
\(∵|PA|+|PB|=|PA'|+|PB'|\)，
\(∴\)当\(A'\),\(B\),\(P\)三点共线时，\(|PA|+|PB|\)取得最小值．
\(\therefore(|P A|+|P B|)_{\min }=\left|A^{\prime} B\right|=4 \sqrt{2+\sqrt{3}}\)
\(=2 \sqrt{2} \cdot \sqrt{4+2 \sqrt{3}}=2 \sqrt{2} \cdot \sqrt{(\sqrt{3}+1)^{2}}=2(\sqrt{2}+\sqrt{6})\)．
\({\color{Red}{(对于形如\sqrt{a+b \sqrt{c}}式子的化简也是运算基本功) }}\)
【点拨】 在解析几何中最值问题也是常见的题型，你试试设点\(P(m,n)\)用函数的方法求解，感受下与本题的几何法比较.我们最好熟悉更多的模型，比如“将军饮马”，它在本题利用点关于直线对称处理了！后面我们在圆的方程、圆锥曲线中也会有.
 

巩固练习

1(★)原点关于\(x-2y+1=0\)的对称点的坐标为\(\underline{\quad \quad}\) ．
 

2(★)已知点\(A(1 ,2)\)、\(B(3 ,1)\)，则线段\(AB\)的垂直平分线的方程是\(\underline{\quad \quad}\) ．
 

3(★)入射光线沿直线\(x－2y+3=0\)射向直线\(l：y=x\)，被\(l\)反射后的光线所在直线的方程是\(\underline{\quad \quad}\) ．
 

4(★)已知\(△ABC\)的顶点\(A(1 ,2)\)，\(AB\)边上的中线\(CM\)所在的直线方程为\(x+2y-1=0\)，\(∠ABC\)的平分线\(BH\)所在直线方程为\(y=x\)，则直线\(BC\)的方程为\(\underline{\quad \quad}\) ．
 

5(★★)已知\(A(3 ,0)\),\(B(0 ,3)\)，从点\(P(0 ,2)\)射出的光线经\(x\)轴反射到时直线\(AB\)上，又经过直线\(AB\)反射回到时P点，则光线所经过的路程为\(\underline{\quad \quad}\) ．
 

6(★★)已知直线\(l\)经过点\(P(6 ,4)\)，斜率为\(k\)
(1)若\(l\)的纵截距是横截距的两倍，求直线\(l\)的方程；
(2)若\(k=-1\)，一条光线从点\(M(6 ,0)\)出发，遇到直线\(l\)反射，反射光线遇到\(y\)轴再次放射回点\(M\)，求光线所经过的路程．
 
 
7(★★)在直线\(l：3x-y-1=0\)上求一点\(P\)，使得：
(1)\(P\)到\(A(4 ,1)\)和\(B(0 ,4)\)的距离之差最大；
(2)\(P\)到\(A(4 ,1)\)和\(C(3 ,4)\)的距离之和最小．
 
 

参考答案

1.\(\left(-\dfrac{2}{5}, \dfrac{4}{5}\right)\)
2.\(4x-2y-5=0\)
3.\(2x-y-3=0\)
4.\(2x-3y-1=0\)
5.\(\sqrt{26}\)
6.\((1) 2x-3y=0\)或\(2x+y-16=0\)\(\text { (2) } 4 \sqrt{17}\)
7.\((1) (2,5) \quad (2) \left(\dfrac{11}{7}, \dfrac{26}{7}\right)\)