4.3 函数的应用

\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步拔高练习，难度3颗星！

模块导图

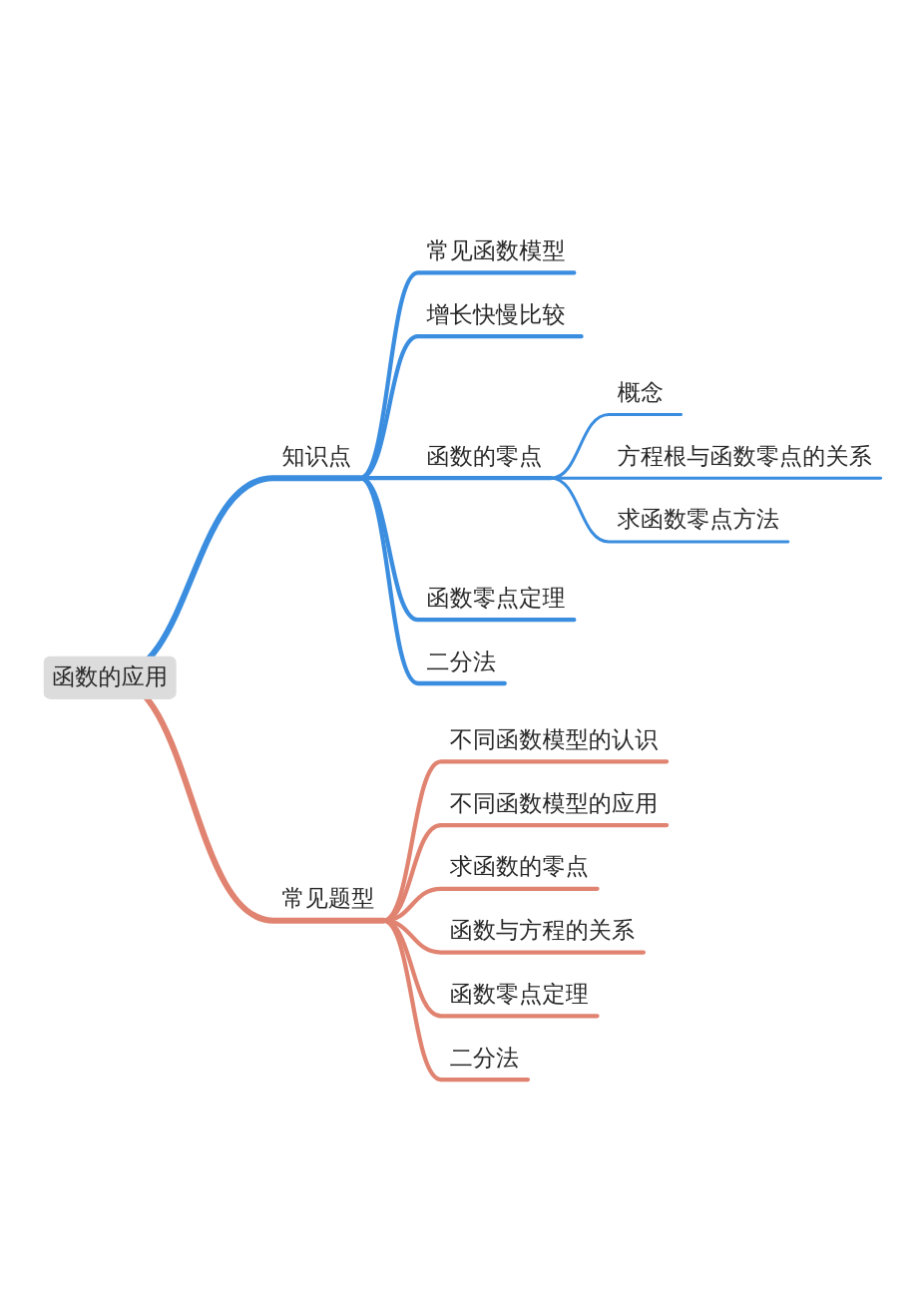
知识剖析

函数模型

 

增长快慢比较

\(V\left(a^{x}\right)>V\left(x^{n}\right)>V\left(\log _{a} x\right)\)
\(V(k x)>V\left(\log _{a} x\right)\)
常见函数图象

 

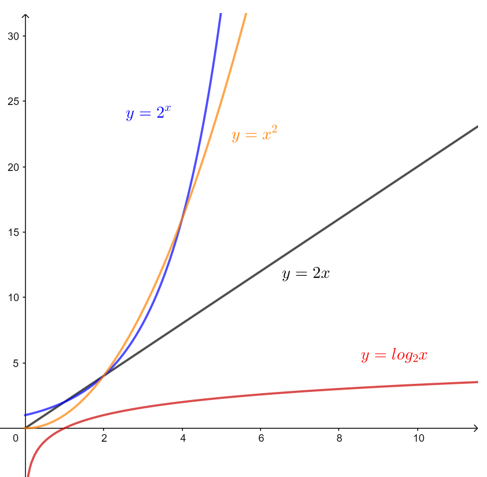
函数的零点

① 函数零点的概念
对于函数\(y=f(x)\)，使\(f(x)=0\)的实数\(x\)叫做函数的零点.
② 方程根与函数零点的关系
方程\(f(x)=0\)有实数根\(x_0\)
\(⇔\)函数\(y=f(x)\)有零点\(x_0\)
\(⇔\)函数\(y=f(x)\)的图象与\(x\)轴有交点，且交点横坐标为\(x_0\).
如 方程\(2^x-4=0\)的实数根是\(x=2\)，
函数\(f(x)=2^x-4\)与\(x\)轴的交点横坐标是\(2\)，
函数\(f(x)=2^x-4\)的零点是\(2\)，而不是\((2 ,0)\).

 

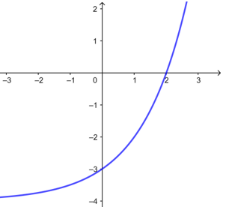
拓展
方程\(f(x)=g(x)\)有实数根\(x_0\)
\(⇔\)函数\(y=f(x)\)与函数\(y=g(x)\)有交点，且交点横坐标为\(x_0\).
\({\color{Red}{解惑}}\) 若让你求解\(x^2-2^x=0\)?可能知道\(x=2\)，那是否只有一个实数根呢？
而方程\(x^2-2^x=0\)的实数根
\(⇔\)函数\(f(x)=x^2\)与函数\(g(x)=2^x\)的交点横坐标
如图就较容易得到，方程\(x^2-2^x=0\)实数根有\(3\)个\(x_1∈(-1 ,0)\),\(x_2=2\)，\(x_3=4\).

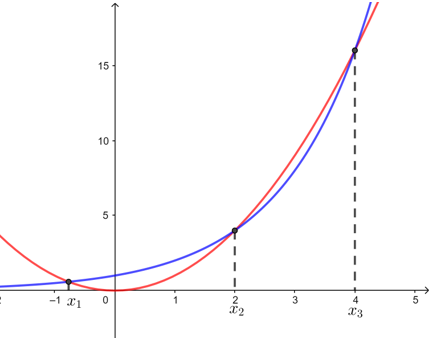
③求函数零点方法
(1) (代数法) 求方程\(f(x)=0\)的实数根.
(2) (几何法) 利用函数的图象，根据函数的性质判断零点是否存在或找出零点位置.
 

函数零点定理

如果函数\(y=f(x)\)在\([a ,b]\)上的图象是连续不断的，且\(f(a)f(b)<0\)，那么函数\(y=f(x)\)在\((a ,b)\)至少有一个零点\(c\)，即存在\(c∈(a ,b)\)，使得\(f(c)=0\)，这个\(c\)也就是方程\(f(x)=0\)的解.

二分法

① 二分法的概念
对于在区间\([a ,b]\)上连续不断且\(f(a)f(b)<0\)的函数\(y=f(x)\)，通过不断地把它的零点所在区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法.
② 用二分法求方程近似解的步骤
\((1)\)确定区间\([a ,b]\)，验证\(f(a)f(b)<0\)，给定精确度ε；
\((2)\)求区间\((a ,b)\)的中点\(c\);
\((3)\)计算\(f(c)\)，
\((i)\)若\(f(c)\), 则\(c\)就是函数的零点；
\((ii)\)若\(f(a)f(c)<0\)，则令\(b=c\)(此时零点\(x_0∈(a ,c)\))
\((iii)\)若\(f(c)f(b)<0\)，则令\(a=c\)(此时零点\(x_0∈(c ,b)\))
\((4)\)判断是否达到精确度\(ε\)：即若\(|a-b|<ε\)，则得到零点近似值为\(a\)(或\(b\))；否则重复\((2)-(4)\).
 

经典例题

【题型一】不同函数模型的认识

【典题1】 惠州市某学校物理兴趣小组在实验测试中收集到一组数据如表所示：

用下列函数中的一个近似地表示这些数据满足的规律，其中最接近的一个是(　　)
A．\(v=\log_2⁡t\) \(\qquad \qquad\)B．\(v=\log _{\frac{1}{2}} t\) \(\qquad \qquad\) C．\(v=\dfrac{t^{2}-1}{2}\) \(\qquad \qquad\)D．\(v=2t-2\)
【解析】 \({\color{Red}{方法1}}\) 由表可知：\(v\)是关于\(t\)的增函数；且增幅随\(t\)的增大而增大，故只有\(C\)满足要求．故选\(C\)．
\({\color{Red} {方法2}}\) 作出散点图，如图，
由函数拟合可知只有\(C\)满足要求．故选\(C\)．

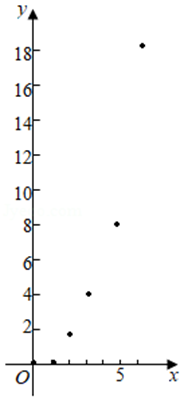
\({\color{Red}{方法3}}\) 由表可知：\(v\)是关于\(t\)的增函数；故\(B\)不适合；
对于\(A\)：\(\log _{2} 1.99 \approx 2\)，\(\log _{2} 3 \approx 0.3\)，\(\log _{2} 4=2\)；故\(A\)不接近；
对于\(C\)：\(\dfrac{1.99^{2}-1}{2} \approx 1.5\)，\(\dfrac{3^{2}-1}{2}=4\)，\(\dfrac{4^{2}-1}{2}=7.5\)，\(\dfrac{5.1^{2}-1}{2} \approx 12.5\)，\(\dfrac{6.12^{2}-1}{2} \approx 18.2\)．故\(C\)接近；
对于\(D\)：\(2×1.99-2=1.98\)，\(2×3-2=4\)，\(2×4-2=6\)，\(2×5.1-2=8.2\)，
\(2×6.12－2=10.24\)，故\(D\)不接近．
故选\(C\)．
【点拨】
判断最佳函数模型，方法如下
① 根据数据的增减性和增幅，排除不符合的函数；
② 根据表格描点做出散点图，结合常见函数模型进行判断；
③ 代点法，把数值代入函数中，若数值偏离较远则排除.
 

【典题2】 假设有一套住房从\(2002\)年的\(20\)万元上涨到\(2012\)年的\(40\)万元．如表给出了两种价格增长方式，其中\(P_1\)是按直线上升的房价，\(P_2\)是按指数增长的房价，\(t\)是\(2002\)年以来经过的年数．

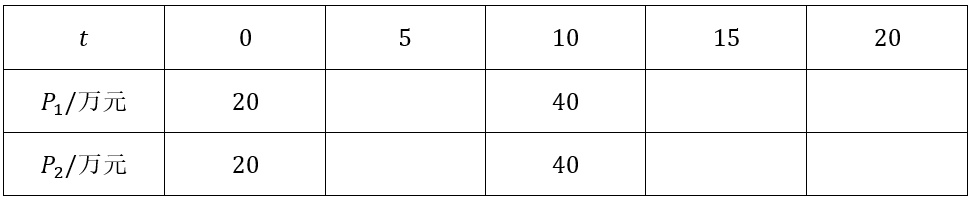
(1)求函数\(P_1=f(t)\)的解析式；
(2)求函数\(P_2=g(t)\)的解析式；
(3)完成上表空格中的数据，并在同一直角坐标系中画出两个函数的图象，然后比较两种
【解析】 (1)由题意可设\(P_1=f(t)=mt+n\)
\(∵\)当\(t=0\)时，\(P_1=20\)；当\(t=10\)时，\(P_1=40\)，
\(\therefore\left\{\begin{array}{l} n=20 \\ 10 m+n=40 \end{array}\right.\)，解得\(\left\{\begin{array}{l} m=2 \\ n=20 \end{array}\right.\)，
\(∴P_1=f(t)=2t+20\)；
(2)由题意可设\(P_2=g(t)=k\cdot a^t\)，
\(∵\)当\(t=0\)时，\(P_2=20\)；当\(t=10\)时，\(P_2=40\)，
\(\therefore\left\{\begin{array}{c} k=20 \\ k \cdot a^{10}=40 \end{array}\right.\)，解得\(\left\{\begin{array}{l} k=20 \\ a=2^{\frac{1}{10}} \end{array}\right.\)，
\(\therefore P_{2}=g(t)=20 \times 2^{\frac{t}{10}}\)；
(3)表中数据如下：

在同一直角坐标系中画出两个函数的图象，如图所示：

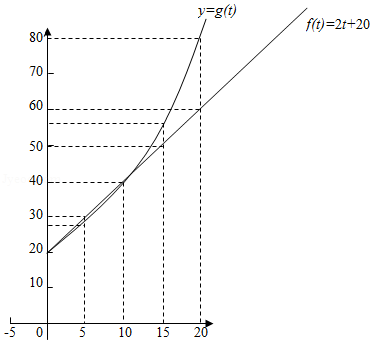
有图象可知，\(P_1=f(t)=2t+20\)呈直线增长，增长速度较慢；\(P_{2}=g(t)=20 \times 2^{\frac{t}{10}}\)呈指数型增长，增长速度较快．
【点拨】 求函数的解析式，当已知函数类型时用“待定系数法”.
 

【题型二】不同函数模型的应用

【典题1】 某地为践行绿水青山就是金山银山的理念，大力开展植树造林．假设一片森林原来的面积为\(a\)亩，计划每年种植一些树苗，且森林面积的年增长率相同，当面积是原来的\(2\)倍时，所用时间是\(10\)年．
(1)求森林面积的年增长率；
(2)到今年为止，森林面积为原来的\(\sqrt{2}\)倍，则该地已经植树造林多少年？
(3)为使森林面积至少达到\(6a\)亩至少需要植树造林多少年？
(参考数据：\(\lg2=0.3010\)，\(lg3=0.4771\))
【解析】 (1)设森林面积的年增长率为\(x\)，
则\(a(1+x)^{10}=2a\)，解得\(x=2^{\frac{1}{10}}-1\)，
\(∴\)森林面积的年增长率为\(2^{\frac{1}{10}}-1\)；
(2)设已经植树造林\(n\)年，则由题意可知\(a(1+x)^{n}=\sqrt{2} a\)，
\(\therefore a \times 2^{\frac{n}{10}}=\sqrt{2} a\)，\(∴n=5\)，
\(∴\)已经植树造林\(5\)年；
(3)设为使森林面积至少达到\(6a\)亩至少需要植树造林\(m\)年，
则\(a(1+x)^{m} \geq 6 a\)，
\(\therefore 2^{\frac{m}{10}} \geq 6\)，
\(\therefore \dfrac{m}{10} \geq \log _{2} 6=\dfrac{\lg 6}{\lg 2}=\dfrac{\lg 2+\lg 3}{\lg 2}\)，
\(\therefore m \geq 10 \times \dfrac{\lg 2+\lg 3}{\lg 2} \approx 26\)，
故为使森林面积至少达到\(6a\)亩至少需要植树造林\(26\)年．
 

【典题2】 新冠肺炎疫情造成医用防护服短缺，某地政府决定为防护服生产企业\(A\)公司扩大生产提供\(x(x∈[0,10])\)(万元)的专项补贴，并以每套\(80\)元的价格收购其生产的全部防护服．\(A\)公司在收到政府\(x\)(万元)补贴后，防护服产量将增加到\(t=k \cdot\left(6-\dfrac{12}{x+4}\right)\)(万件)，其中\(k\)为工厂工人的复工率\((k∈[0,5.1])\)．\(A\)公司生产\(t\)万件防护服还需投入成本\((20+8x+50t)\)(万元)．
(1)将\(A\)公司生产防护服的利润\(y\)(万元)表示为补贴\(x\)(万元)的函数；
(2)对任意的\(x∈[0,10]\)(万元)，当复工率\(k\)达到多少时，\(A\)公司才能不产生亏损？(精确到\(0.01\))．
【解析】 (1)\(y=80t-(20+8x+50t)=30t-20-8x\)
\(=30 k\left(6-\dfrac{12}{x+4}\right)-20-8 x\)
\(=180 k-\dfrac{360 k}{x+4}-8 x-20\)，\(x∈[0,10]\)．
(2)若对任意的\(x∈[0,10]\)，公司都不产生亏损，
则\(180 k-\dfrac{360 k}{x+4}-8 x-20 \geq 0\)在\(x∈[0,10]\)恒成立，
即\(k \geq \dfrac{1}{45} \cdot \dfrac{(x+4)(2 x+5)}{x+2}\)， \({\color{Red}{(分离参数法) }}\)
记\(t=x+2\)，则\(t∈[2,12]\)，
此时\(\dfrac{(x+4)(2 x+5)}{x+2}=\dfrac{(t+2)(2 t+1)}{t}=2 t+\dfrac{2}{t}+5\)
由于函数\(f(t)=2 t+\dfrac{2}{t}+5\)在\(t∈[2,12]\)单调递增， \({\color{Red}{(对勾函数)}}\)
所以当\(t∈[2,12]\)时，\(f_{\max }(t)=f(12)=29+\dfrac{1}{6} \approx 29.167\)，
\(\therefore k \geq \dfrac{1}{45} \times 29.167 \approx 0.648\)，
即当工厂工人的复工率达到\(0.65\)时，对任意的\(x∈[0,10]\)，公司都不产生亏损．
【点拨】
① 根据题意求出函数的解析式，在实际问题中，特别注意自变量的取值范围；
② 求函数\(y=\dfrac{a x^{2}+b x+c}{a_{1} x^{2}+b_{1} x+c_{1}}\)最值问题中，注意基本不等式和对勾函数的应用.
 

巩固练习

1(★) 有一组实验数据如表：

则体现这些数据的最佳函数模型是(　　)
A．\(y=x^{\frac{1}{2}}\) \(\qquad \qquad\) B．\(y=\log _{2} x\) \(\qquad \qquad\) C．\(y=\dfrac{1}{3} \cdot 2^{x}\) \(\qquad \qquad\)D．\(y=\dfrac{1}{2} x^{2}\)
 

2(★) 设光线通过一块玻璃，强度损失\(10 \%\)、如果光线原来的强度为\(k(k>0)\)，通过\(x\)块这样的玻璃以后强度为\(y\)，则\(y=k \cdot 0.9^{x}\left(x \in \boldsymbol{N}^{*}\right)\)，那么光线强度减弱到原来的\(\dfrac{1}{3}\)以下时，至少通过这样的玻璃块数为(　　)(参考数据：\(1 g 3 \approx 0.477)\))
A．\(9\) \(\qquad \qquad \qquad \qquad\) B．\(10\) \(\qquad \qquad \qquad \qquad\)C．\(11\) \(\qquad \qquad \qquad \qquad\) D．\(12\)
 

3(★★) 某地区今年\(1\)月，\(2\)月，\(3\)月患某种传染病的人数分别为\(42\)，\(48\)，\(52\)．为了预测以后各月的患病人数，甲选择了模型\(y=ax^2+bx+c\)，乙选择了模型\(y=pq^x+r\)，其中\(y\)为患病人数，\(x\)为月份数，\(a\)，\(b\)，\(c\)，\(p\)，\(q\)，\(r\)都是常数．结果\(4\)月，\(5\)月，\(6\)月份的患病人数分别为\(54\)，\(57\)，\(58\)．
(1)求\(a\)，\(b\)，\(c\)，\(p\)，\(q\)，\(r\)的值；
(2)你认为谁选择的模型好．
 
 

4(★★)某心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其注意力指数\(p\)与听课时间\(t\)之间的关系满足如图所示的曲线．当\(t∈(0,14]\)时，曲线是二次函数图象的一部分，当\(t∈[14,40]\)时，曲线是函数\(y=\log _{a}(t-5)+83\)(\(a>0\),且\(a≠1\))图象的一部分．根据专家研究，当注意力指数\(p\)大于等于\(80\)时听课效果最佳．
(1)试求\(p=f(t)\)的函数关系式；
(2)一道数学难题，讲解需要\(22\)分钟，问老师能否经过合理安排在学生听课效果最佳时讲完？请说明理由．
 
 

5(★★)培养某种水生植物需要定期向培养植物的水中加入物质\(N\)．已知向水中每投放\(1\)个单位的物质\(N\)，\(x\)(单位：天)时刻后水中含有物质\(N\)的量增加\(y mol/L\)，\(y\)与\(x\)的函数关系可近似地表示为\(y=\left\{\begin{array}{l} 8-\dfrac{16}{x+2}, 0 \leq x \leq 6 \\ 12-x, 6<x \leq 12 \end{array}\right.\)．根据经验，当水中含有物质\(N\)的量不低于\(4mol/L\)时，物质\(N\)才能有效发挥作用．
(1)若在水中首次投放\(1\)个单位的物质\(N\)，计算物质\(N\)能持续有效发挥作用几天？
(2)若在水中首次投放\(1\)个单位的物质\(N\)，第\(8\)天再投放\(1\)个单位的物质\(N\)，试判断第\(8\)天至第\(12\)天，水中所含物质\(N\)的量是否始终不超过\(6mol/L\)，并说明理由．
 
 

参考答案

1.\(C\)

2.\(C\)

3.\((1) a=-1\)，\(b=9\)，\(c=34\),\(p=-27\)，\(q=\dfrac{2}{3}\)，\(r=60\)(2) 乙模型

4.\(\text { (1) } f(t)=\left\{\begin{array}{l} -\dfrac{1}{4}(t-12)^{2}+82, t \in(0,14] \\ \log _{\dfrac{1}{3}}(t-5)+83, t \in(14,40] \end{array}\right.\)

\((2)\)教师能够合理安排时间讲完题目

5.\((1)6\)
\((2)\)第\(8\)天至第\(12\)天，水中所含物质\(N\)的量始终不超过\(6mol/L\)
 

【题型三】求函数的零点

【典题1】 下列函数中，在\((-1 ,1)\)内有零点且单调递增的是(　　)
A．\(y=\log _{\dfrac{1}{3}} x\) \(\qquad \qquad \qquad\)B．\(y=3^x-1\) \(\qquad \qquad \qquad\)C．\(y=x^{2}-\dfrac{1}{2}\) \(\qquad \qquad \qquad\)D．\(y=-x^3\)
【解析】 根据题意，依次分析选项：
对于\(A\)，\(y=\log _{\dfrac{1}{3}} x\)，其定义域为\((0 ,+∞)\)，在\((-1 ,0)\)上没有定义，不符合题意；
对于\(B\)，\(y=3^x-1\)，在\((-1 ,1)\)上有零点\(x=0\)，且在\((-1 ,1)\)为增函数，符合题意；
对于\(C\)，\(y=x^{2}-\dfrac{1}{2}\)，为二次函数，在\((-1 ,0)\)上为减函数，不符合题意；
对于\(D\)，\(y=-x^3\)，在\((-1 ,1)\)上为减函数，不符合题意；
故选：\(B\)．
【点拨】 求函数零点方法：① 代数法，即解方程；② 几何法，即数形结合.
 

【题型四】函数与方程的关系

【典题1】 方程\(3^x+4^x=5^x\)解的情况是( )
A.有且只有一个根\(2\) \(\qquad \qquad \qquad \qquad\)B.不仅有根\(2\)还有其他根
C.有根\(2\)和另一个负根 \(\qquad \qquad \qquad \qquad\)D.有根\(2\)和另一个正根
【解析】方程\(3^x+4^x=5^x\)等价为\(\left(\dfrac{3}{5}\right)^{x}+\left(\dfrac{4}{5}\right)^{x}=1\)
设\(f(x)=\left(\dfrac{3}{5}\right)^{x}+\left(\dfrac{4}{5}\right)^{x}\)，
则函数\(f(x)\)在\(R\)上为减函数，
\(∵f(2)=\left(\dfrac{3}{5}\right)^{2}+\left(\dfrac{4}{5}\right)^{2}=1\)
\(∴\)方程\(3^x+4^x=5^x\)有且只有一个根\(2\)，故选\(A\).
【点拨】 本题巧妙的把方程\(3^x+4^x=5^x\)的解转化为函数\(f(x)=\left(\dfrac{3}{5}\right)^{x}+\left(\dfrac{4}{5}\right)^{x}\)与\(y=1\)的交点问题.
 

【典题2】 若\(x_1\)满足\(3^x=2-x\)，\(x_2\)满足\(\log_3⁡x+x-2=0\)，则\(x_1+x_2=\).
【解析】 设\(f(x)=3^x\)，\(g(x)=\log _{3} x\)，\(t(x)=2-x\)
\(∵x_1\)满足\(3^x=2-x\)，
\(∴ x_1\)是函数\(f(x)=3^x\)与函数\(t(x)=2-x\)交点横坐标，
\(∵x_2\)满足\(\log_3⁡x+x-2=0\)，
\(∴ x_2\)是函数\(g(x)=\log _{3} x\)与函数\(t(x)=2-x\)交点横坐标，
由于函数\(y=3^t\)与函数\(y=\log_3⁡t\)互为反函数，
所以它们的图象关于直线\(y=x\)轴对称，
故两图象与直线\(t(x)=2-x\)的交点\((x_1 ,y_1)\),\((x_2 ,y_2)\)也关于\(y=x\)对称，
所以\(x_1+x_2=2\).

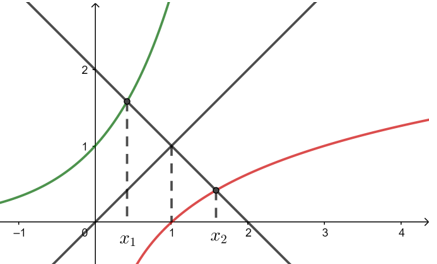
【点拨】
① 指数函数\(y=a^x\)与对数函数\(y=\log_a x\)互为反函数，它们的图象关于直线\(y=x\)对称.
② 方程问题转化为函数问题时，在构造函数时，常把常见的函数模型(一次函数型、二次函数型、反比例函数型，指数函数型、对数函数型等)分开，比如方程\((x+1) 2^x+3=0\)\(⇔\)函数\(y=2^x\)与函数\(y=-\dfrac{3}{x+1}\)，方程\(e^{x}|\ln x|-k=0\)\(⇔\)函数\(y=|lnx|\)与函数\(y=k \cdot\left(\dfrac{1}{e}\right)^{x}\).
 

【典题3】 已知函数\(f(x)=\left\{\begin{array}{l} \left|\log _{2} x\right|, x>0 \\ x^{2}+4 x+1, x \leq 0 \end{array}\right.\)，若函数\(F(x)=f(x)-b\)有四个不同的零点\(x_1\)，\(x_2\)，\(x_3\)，\(x_4\)\((x_1<x_2<x_3<x_4)\)，则\(\dfrac{x_{4}}{x_{3}}-\dfrac{x_{1} x_{3}^{2}+x_{2} x_{3}^{2}}{4}\)的取值范围是\(\underline{\quad \quad }\) .
【解析】 \({\color{Red}{(函数F(x)=f(x)-b的零点等价于函数y=f(x)与y=b的交点)}}\)
作出\(f(x)\)的函数图象如图所示，

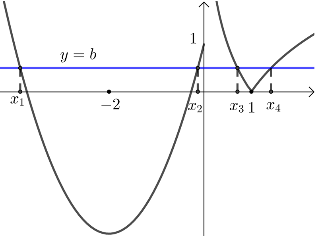
由图象知\(x_1+x_2=-4\)，\(x_3 x_4=1\)，\(0<b≤1\)，
而\(0<-\log _{2} x_{3} \leq 1\)得\(\dfrac{1}{2} \leq x_{3}<1\)，
\(\therefore \dfrac{x_{4}}{x_{3}}-\dfrac{x_{1} x_{3}^{2}+x_{2} x_{3}^{2}}{4}=\dfrac{1}{x_{3}^{2}}+x_{3}^{2}\)，
令\(t=x_3^2\)，则\(\dfrac{1}{4} \leq t<1\)，
令\(g(t)=t+\dfrac{1}{t}\)，
则\(g(t)\)在\(\left[\dfrac{1}{4}, 1\right]\)上单调递减，\(g(1)=2\)，\(g\left(\dfrac{1}{4}\right)=\dfrac{17}{4}\),
\(\therefore g(1)<g(t) \leq g\left(\dfrac{1}{4}\right)\)，
即\(2<t+\dfrac{1}{t} \leq \dfrac{17}{4}\).
【点拨】
① 函数\(F(x)=f(x)－b\)零点的问题转化为函数\(y=f(x)\)与\(y=b\)的交点问题；
② 遇到分段函数常常需要数形结合；
③ 求\(\dfrac{x_{4}}{x_{3}}-\dfrac{x_{1} x_{3}^{2}+x_{2} x_{3}^{2}}{4}\)的取值范围，应该根据图象找出\(x_1+x_2=-4\)，\(x_3 x_4=1\)的关系，在利用“消元”的思想把问题化简成“求\(\dfrac{1}{x_{3}^{2}}+x_{3}^{2}\)的取值范围”，从而想到构造函数\(g(t)=t+\dfrac{1}{t}\).
 

【典题4】 已知偶函数\(f(x)\)满足\(f(3+x)=f(3-x)\)，且当\(x∈[0 ,3]\)时，\(f(x)=-x^2+2x+1\)，若关于\(x\)的方程\(f^2 (x)-tf(x)－3=0\)在\([-150 ,150]\)上有\(300\)个解，则实数\(t\)的取值范围是\(\underline{\quad \quad }\).
【解析】 \(∵f(x)\)是偶函数，\(∴f(3+x)=f(3-x)=f(x-3)\)，
\(∴f(x)\)是以\(6\)为周期的函数．
\(∵\)关于\(x\)的方程\(f^2 (x)-tf(x)-3=0\)在\([-150 ,150]\)上有\(300\)个解，
\(∴\)关于\(x\)的方程\(f^2 (x)-tf(x)-3=0\)在\((-3 ,3]\)上有\(6\)个解．
做出\(f(x)\)在一个周期\((-3 ,3]\)上的函数图象如图所示：

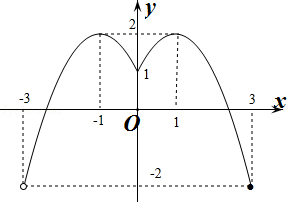
令\(f(x)=m\)，由函数图象可知：
当\(m=-2\)时，\(f(x)=m\)只有\(1\)解，
当\(-2<m<1\)或\(m=2\)时，\(f(x)=m\)有\(2\)解，
当\(m=1\)时，\(f(x)=m\)有\(3\)解，
当\(1<m<2\)时，\(f(x)=m\)有\(4\)解．
\(∴\)关于\(m\)的方程\(m^2-tm-3=0\)在\(\{2\}\)和\((1，2)\)上各有\(1\)解或\((－2 ,1)\)和\((1 ,2)\)上各有1解，
若方程的一解为\(m=2\)，则方程的另一解为\(m=-\dfrac{3}{2} \notin(1,2)\)，不符合题意．
\(∴\)关于\(m\)的方程\(m^2-tm-3=0\)在\((－2 ,1)\)和\((1 ,2)\)上各有\(1\)解，
\(\therefore\left\{\begin{array}{l} 1+2 t>0 \\ -2-t<0 \\ 1-2 t>0 \end{array}\right.\)，解得\(-\dfrac{1}{2}<t<\dfrac{1}{2}\)．
【点拨】
① 由\(f(3+x)=f(3-x)\)可得\(f(x)\)关于\(x=3\)对称，又由于\(f(x)\)是偶函数，可得函数的周期\(T=6\)；
② 在“关于\(x\)的方程\(f^2 (x)-tf(x)-3=0\)在\((-3 ,3]\)上有\(6\)个解”这一步中的区间是\((-3 ,3]\)，不能是\([-3 ,3]\).
 

巩固练习

1(★) 下列函数中，是偶函数且不存在零点的是(　　)
A．\(y=x^2\) \(\qquad \qquad\)B．\(y=\sqrt{x}\) \(\qquad \qquad\)C．\(y=\log_2⁡x\) \(\qquad \qquad\)D．\(y=-\left(\dfrac{1}{2}\right)^{|x|}\)

 

2(★★) 函数\(f(x)=\left(\dfrac{1}{2}\right)^{|x|}-x^{2}\)的零点个数是\(\underline{\quad \quad }\)．
 

3(★★) 若方程\(m^x-x-m=0\)(\(m>0\), 且\(m≠1\))有两个不同实数根，则\(m\)的取值范围是\(\underline{\quad \quad }\)．
 

4(★★) 设\(a\)、\(b\)、\(c\)依次表示函数\(f(x)=x^{\frac{1}{2}}-x+1\)，\(g(x)=\log _{\frac{1}{2}} x-x+1\)，\(h(x)=\left(\dfrac{1}{2}\right)^{x}-x+1\)的零点，则\(a\)、\(b\)、\(c\)的大小关系为\(\underline{\quad \quad }\)．
 

5(★★★) 已知函数\(f(x)=\log_3⁡x\)，函数\(h(x)\)是最小正周期为\(2\)的偶函数，且当\(x∈[0 ,1]\)时，\(h(x)=3^x-1\)．若函数\(y=k\cdot f(x)+h(x)\)有\(3\)个零点，则实数\(k\)的取值范围是\(\underline{\quad \quad }\)．
 

6(★★★) 已知函数\(f(x)=\left\{\begin{array}{l} \left|5^{x}-1\right|, x<1 \\ \dfrac{8}{x+1}, x \geq 1 \end{array}\right.\)，若方程\(f(f(x))=a\)恰有\(5\)个不同的实数根，则实数\(a\)的取值范围为\(\underline{\quad \quad }\)．
 
 

参考答案

1.\(D\)
2.\(2\)
3.\(m>1\)
4.\(b<c<a\)
5.\(\left(-2,-2 \log _{5} 3\right)\)
6.\(\left(\dfrac{8}{5}, 4\right)\)

 

【题型五】函数零点定理

【典题1】 设函数\(f(x)=\dfrac{2 x}{x+1}+\ln x\)满足\(f(a)f(b)f(c)<0\)\((a<b<c)\)，若\(f(x)\)存在零点\(x_0\)，则下列选项中一定错误的是(　　)
A．\(x_0∈(a ,c)\) \(\qquad \qquad\) B．\(x_0∈(a ,b)\) \(\qquad \qquad\) C．\(x_0∈(b ,c)\) \(\qquad \qquad\) D．\(x_0∈(c ,+∞)\)
【解析】 函数函数\(f(x)=\dfrac{2 x}{x+1}+\ln x\)的定义域为\(\{x|x>0\}\)，函数是增函数，
满足\(f(a)f(b)f(c)<0(a<b<c)\)，说明\(f(a)\),\(f(b)\),\(f(c)\)有\(1\)个是负数两个正数(且负数一定是\(f(a)\))或\(3\)个负数，由函数的零点判断定理可知，函数的零点在\((a ,c)\)，在\((a ,b)\)，在\((c ,+∞)\)，不可能在\((b ,c)\)．
故选\(C\)．
【点拨】
①\(\dfrac{2 x}{x+1}=2-\dfrac{2}{x+1}\)利用了分离常数法.
② 判断函数零点所在的区间，就要注意区间上端点对应的函数值(本题中\(f(a)\)、\(f(b)\)、\(f(c)\))是正数还是负数.

 

【典题2】 \([x]\)表示不超过\(x\)的最大整数，例如\([3.5]=3\)，\([－0.5]=-1\)．已知\(x_0\)是方程\(\ln x+3x－15=0\)的根，则\([x_0]=\) \(\underline{\quad \quad }\)．
【解析】 \(x_0\)是方程\(\ln x+3x－15=0\)的根，
设\(f(x)=\ln x+3x－15\)，显然\(f(x)\)单调递增，
故\(f(x)=0\)只有一个根，
\(f(4)=\ln 4-3=2 \ln 2-3<2(\ln 2-1)<0\)
\(f(5)=\ln 5>0\)
故\(x_0∈(4 ,5)\)，所以\([x_0]=4\).
【点拨】
① 若\(f(x)\)在\([a ,b]\)上是单调函数，则它在\([a ,b]\)上至多只有一个零点.
② 求函数零点的近似值，可利用代入一些数值进行逼近，再用函数的零点判断定理确认零点的范围.
 

【题型六】二分法

【典题1】 用二分法求函数\(f(x)=\ln(x+1)+x-1\)在区间\([0 ,1]\)上的零点，要求精确度为\(0.01\)时，所需二分区间的次数最少为\(\underline{\quad \quad }\)．
【解析】 根据题意，原来区间\([0 ,1]\)的长度等于\(1\)，每经过二分法的一次操作，区间长度变为原来的一半，则经过\(n\)次操作后，区间的长度为\(\dfrac{1}{2^{n}}\)，若\(\dfrac{1}{2^{n}}<0.01\)，即\(n≥7\)；
故最少为\(7\)次.
【点拨】 二分法每一次操作都会让区间缩小一半长度.
 

巩固练习

1(★) 设函数\(f(x)=e^x+\ln x\)，满足\(f(a)f(b)f(c)<0\)\((a<b<c)\)，若\(f(x)\)存在零点\(x_0\)，则下列选项中一定错误的是(　　)
A．\(x_0∈(a ,c)\) \(\qquad \qquad\) B．\(x_0∈(a ,b)\) \(\qquad \qquad\) C．\(x_0∈(b ,c)\) \(\qquad \qquad\) D．\(x_0∈(c ,+∞)\)
 

2(★★) [多选题]函数\(f(x)=x^3+3x-2\)的一个正零点所在的区间不可能是(　　)
A．\((3 ,4)\)\(\qquad \qquad \qquad \qquad\) B．\((2 ,3)\) \(\qquad \qquad \qquad \qquad\) C．\((1 ,2)\) \(\qquad \qquad \qquad \qquad\) D．\((0 ,1)\)
 

3(★★) 已知函数\(f(x)=\log_2⁡x+x﹣b\)的零点在区间\([0 ,1]\)上，则\(b\)的取值范围为\(\underline{\quad \quad }\)．
 

4(★★) 若函数\(f(x)=x^2+tx+1\)在区间\((1 ,2)\)上有一个零点，则实数\(t\)的取值范围是\(\underline{\quad \quad }\)．
 
 

参考答案

1.\(C\)
2.\(ABC\)
3.\((-∞ ,1]\)
4.\((-\dfrac{5}{2},-2)\)