高一函数专题 函数的周期性和对称性
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步拔高练习,难度3颗星!
模块导图
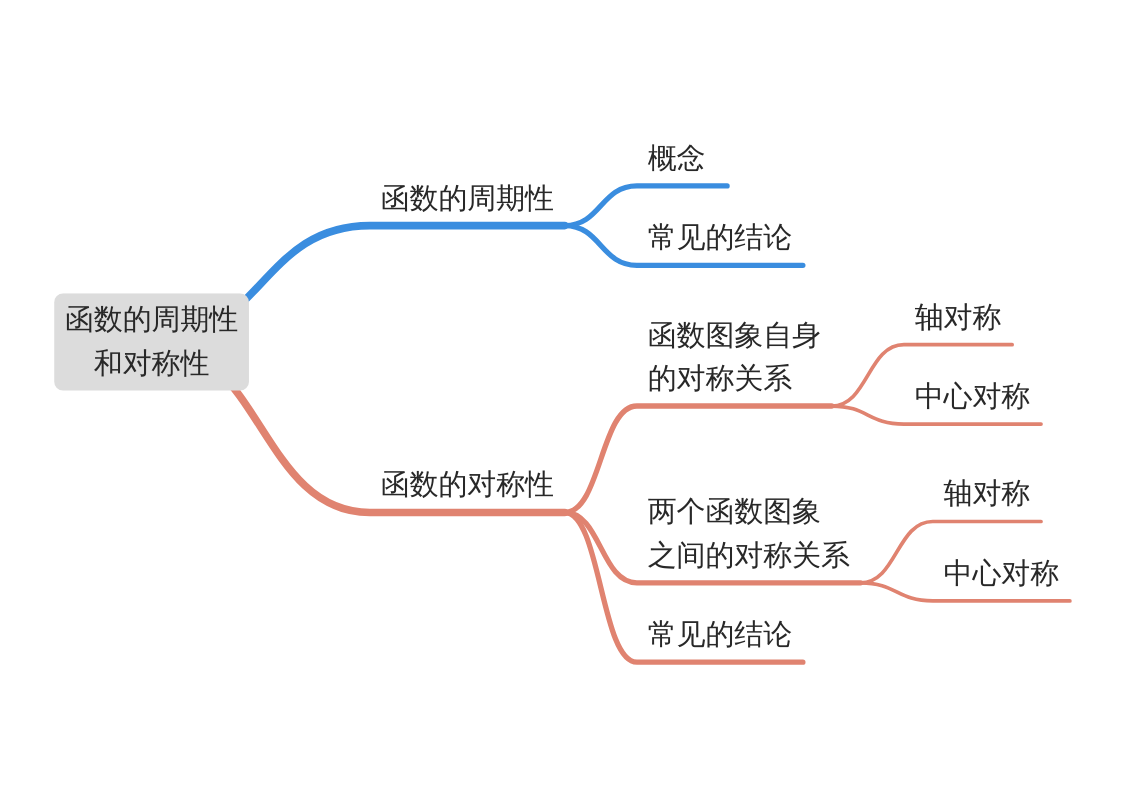
知识剖析
函数的周期性
1 概念
对于函数\(y=f(x)\),如果存在一个不为零的常数\(T\),使得当\(x\)取定义域内的每一个值时,\(f(x+T)=f(x)\)都成立,那么把函数\(y=f(x)\)叫做周期函数,常数\(T\)叫做这个函数的周期.
\({\color{Red}{ Eg }}\)
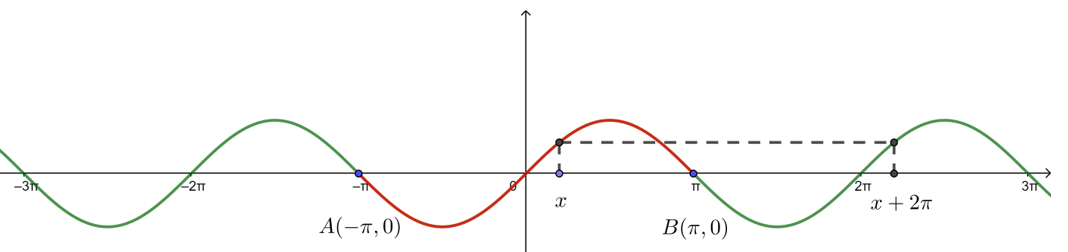
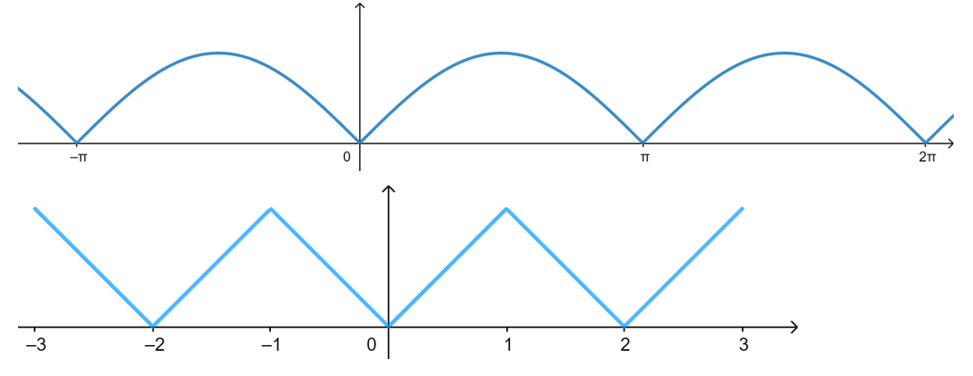
2 常见的结论
① 若\(f(x+a)=f(x+b)\),则\(y=f(x)\)的周期是\(T=a-b\)
② 若\(f(x+a)=-f(x)\),则\(y=f(x)\)的周期是\(T=2a\)
\({\color{Red}{(你可证明试试)}}\)
③ 若\(f(x+a)=\dfrac{1}{f(x)}\),则\(y=f(x)\)的周期是\(T=2a\)
函数的对称性
函数图象自身的对称关系
1 轴对称
若\(f(x+a)=f(b-x)\), 则\(y=f(x)\)有对称轴\(x=\dfrac{a+b}{2}\)
2 中心对称
若函数\(y=f(x)\)定义域为\(R\),且满足条件\(f(a+x)+f(b-x)=c\)(\(a\),\(b\),\(c\)为常数),则函数\(y=f(x)\)的图象关于点\(\left(\dfrac{a+b}{2}, \dfrac{c}{2}\right)\)对称.

两个函数图象之间的对称关系
1 轴对称
若函数\(y=f(x)\)定义域为\(R\),则两函数\(y=f(x+a)\)与\(y=f(b-x)\)的图象关于直线\(x=\dfrac{b-a}{2}\)对称.
特殊地,函数\(y=f(a+x)\)与函数\(y=f(a-x)\)的图象关于直\(x=0\)对称.
2 中心对称
若函数\(y=f(x)\)定义域为\(R\),则两函数\(y=f(a+x)\)与\(y=c-f(b-x)\)的图象关于点\(\left(\dfrac{b-a}{2}, \dfrac{c}{2}\right)\)对称.
特殊地,函数\(y=f(x+a)\)与函数\(y=-f(b-x)\)图象关于点\(\left(\dfrac{b-a}{2}, 0\right)\)对称.
周期性与对称性拓展
\((1)\)若函数\(y=f(x)\)同时关于直线\(x=a\),\(x=b\)对称,则函数\(y=f(x)\)的周期\(T=2|b-a|\);特殊地,若偶函数\(y=f(x)\)的图像关于直线\(x=a\)对称,则函数\(y=f(x)\)的周期\(T=2|a|\);
\((2)\)若函数\(y=f(x)\)同时关于点\((a ,0)\),\((b ,0)\)对称,则函数\(y=f(x)\)的周期\(T=2|b-a|\);
\((3)\)若函数\(y=f(x)\)同时关于直线\(x=a\)对称,又关于点\((b ,0)\)对称 , 则函数\(y=f(x)\)的周期
\(T=4|b-a|\);
特殊地,若奇函数\(y=f(x)\)的图像关于直线\(x=a\)对称,则函数\(y=f(x)\)的周期\(T=4|a|\).
经典例题
【题型一】函数的周期性
【典题1】 设\(f(x)\)是周期为\(4\)的奇函数,当\(0≤x≤1\)时,\(f(x)=x(1+x)\),则\(f\left(-\dfrac{9}{2}\right)=\) \(\underline{\quad \quad }\)
【解析】 \(∵f(x)\)是周期为\(4\)的奇函数,
当\(0≤x≤1\)时,\(f(x)=x(1+x)\),
\(\therefore f\left(-\dfrac{9}{2}\right)=f\left(-\dfrac{9}{2}+4\right)=f\left(-\dfrac{1}{2}\right)\)\(=-f\left(\dfrac{1}{2}\right)=-\dfrac{1}{2}\left(1+\dfrac{1}{2}\right)=-\dfrac{3}{4}\).
【典题2】 设偶函数\(f(x)\)对任意\(x∈R\),都有\(f(x+3)=-\dfrac{1}{f(x)}\),且当\(x∈[-3 ,-2]\)时,\(f(x)=4x\),则\(f(107.5)=\) \(\underline{\quad \quad }\).
【解析】 \(∵f(x+3)=-\dfrac{1}{f(x)}\),
\(\therefore f(x+6)=-\dfrac{1}{f(x+3)}=-\dfrac{1}{-\frac{1}{f(x)}}=f(x)\),
\(∴\)函数\(f(x)\)是以\(6\)为周期的函数.
\(∵\)当\(x∈[-3 ,-2]\)时,\(f(x)=4x\),
\(\therefore f(107.5)=f(6 \times 17+5.5)=f(5.5)=-\dfrac{1}{f(2.5)}\)\(=-\dfrac{1}{f(-2.5)}=-\dfrac{1}{4 \times(-2.5)}=\dfrac{1}{10}\).
故答案为\(\dfrac{1}{10}\).
【点拨】
① 在求值过程中,比如本题中求\(f(107.5)\),先用函数周期性把\(107.5\)这个数值变小些,尽量向\([-3 ,-2]\)靠拢.
② 函数综合性的题型,可用数形结合的方法找到思考的方向.
巩固练习
1 (★★) 已知定义在\(R\)上的奇函数\(f(x)\),满足\(f(x+4)=-f(x)\),且在\([0 ,2]\)上单调递减,则( )
A.\(f(8)<f(11)<f(15)\)\(\qquad \qquad \qquad\)B.\(f(11)<f(8)<f(15)\)\(\qquad \qquad\)
C.\(f(15)<f(11)<f(8)\)\(\qquad \qquad \qquad\)D.\(f(15)<f(8)<f(11)\)
2 (★★) 已知\(f(x)\)是定义在\(R\)上周期为\(2\)的函数,当\(x∈[-1 ,1]\)时,\(f(x)=|x|\),那么当\(x∈[-7 ,-5]\)时,\(f(x)=\) \(\underline{\quad \quad }\).
3 (★★★) 设函数\(f(x)\)是定义在\(R\)上的奇函数,满足\(f(x+1)=-f(x-1)\),若\(f(-1)>1\),
\(f(5)=a^2-2a-4\),则实数\(a\)的取值范围是\(\underline{\quad \quad }\).
参考答案
1.\(B\)
2.\(|x+6|\)
3.\((-1 ,3)\)
【题型二】函数图象自身的对称关系
【典题1】 定义在\(R\)上的函数\(f(x)\)的图象关于点\(\left(-\dfrac{3}{4}, 0\right)\)成中心对称且对任意的实数\(x\)都有\(f(x)=-f\left(x+\dfrac{3}{2}\right)\)且\(f(-1)=1\),\(f(0)=-2\),则\(f(1)+f(2)+⋯+f(2014)=\) \(\underline{\quad \quad }\).
【解析】 \(∵f(x)=-f\left(x+\dfrac{3}{2}\right)\),
\(\therefore f\left(x+\dfrac{3}{2}\right)=-f(x)\),
则\(f(x+3)=-f\left(x+\dfrac{3}{2}\right)=f(x)\)
\(∴f(x)\)是周期为\(3\)的周期函数.
\({\color{Red}{(确定周期后,接着求前三项和f(1)+f(2)+f(3)便可)}}\)
则\(f(2)=f(-1+3)=f(-1)=1\),\(f\left(\dfrac{1}{2}\right)=-f(-1)=-1\)
\(∵\)函数\(f(x)\)的图象关于点\(\left(-\dfrac{3}{4}, 0\right)\)成中心对称,
\(\therefore f(1)=-f\left(-\dfrac{5}{2}\right)=-f\left(\dfrac{1}{2}\right)=1\)
\(∵f(3)=f(0)=-2\)
\(∴f(1)+f(2)+f(3)=1+1-2=0\)
\(∴f(1)+f(2)+⋯+f(2014)=f(1)=1\)
【典题2】 已知函数\(f(x)=\dfrac{2 x^{2}}{x^{2}-4 x+8}\),则( )
A.函数\(f(x)\)的图象关于\(x=2\)对称 \(\qquad \qquad \qquad \qquad\)B.函数\(f(x)\)的图象关于\(x=4\)对称
C.函数\(f(x)\)的图象关于\((2 ,2)\)对称 \(\qquad \qquad \qquad \qquad\)D.函数\(f(x)\)的图象关于\((4 ,4)\)对称
【解析】 \({\color{Red}{方法一 利用函数平移和奇偶性}}\)
对于A选项:若函数\(f(x)\)的图象关于\(x=2\)对称,
则\(y=f(x+2)\)是偶函数,
而\(y=f(x+2)=\dfrac{2(x+2)^{2}}{x^{2}+4}\)不是偶函数,
\(∴A\)错误;
对于\(B\)选项,可以采取类似选项\(A\)的方法排除;
对于\(C\)选项:若函数\(f(x)\)的图象关于\((2 ,2)\)对称,则函数向左和向下均平移\(2\)个单位的函数关于原点对称,即\(y=f(x+2)-2\)是奇函数.
易得\(y=f(x+2)-2=\dfrac{2(x+2)^{2}}{x^{2}+4}-2=\dfrac{8 x}{x^{2}+4}\)是奇函数,
\(∴C\)正确;
对于\(D\)选项:若函数\(f(x)\)的图象关于\((4 ,4)\)对称,则函数向左和向下均平移\(4\)个单位的函数关于原点对称,即\(y=f(x+4)-4\)是奇函数.
而\(y=f(x+4)-4=\dfrac{2(x+4)^{2}}{(x+2)^{2}+4}-4=-\dfrac{2 x^{2}}{(x+2)^{2}+4}\)
不是奇函数,
\(∴D\)错误.
故选\(C\).
\({\color{Red}{方法二 利用函数自身的轴对称和中心对称关系}}\)
利用函数自身的轴对称关系:若\(f(x+a)=f(b-x)\), 则\(y=f(x)\)有对称轴\(x=\dfrac{a+b}{2}\).
对于\(A\)选项:若函数\(f(x)\)的图象关于\(x=2\)对称,
则有\(f(4-x)=f(x)\)
而\(f(4-x)=\dfrac{2(4-x)^{2}}{(4-x)^{2}-4(4-x)+8}\)\(=\dfrac{2(4-x)^{2}}{x^{2}-4 x+8} \neq \dfrac{2 x^{2}}{x^{2}-4 x+8}=f(x)\),
\(∴A\)错误;
对于\(B\)选项:若函数\(f(x)\)的图象关于\(x=4\)对称,
则有\(f(8-x)=f(x)\),
而\(f(8-x)=\dfrac{2(8-x)^{2}}{(8-x)^{2}-4(8-x)+8}\)\(=\dfrac{2(8-x)^{2}}{x^{2}-12 x+40} \neq \dfrac{2 x^{2}}{x^{2}-4 x+8}=f(x)\),
\(∴B\)错误;
利用函数自身的中心对称关系:
若\(f(a+x)+f(b-x)=c\)(\(a\),\(b\),\(c\)为常数),
则函数\(f(x)\)的图象关于点\(\left(\dfrac{a+b}{2}, \dfrac{c}{2}\right)\)对称.
对于\(C\)选项:若函数\(f(x)\)的图象关于\((2 ,2)\)对称,
则\(f(x)+f(4-x)=4\),
易得\(f(x)+f(4-x)\)\(=\dfrac{2 x^{2}}{x^{2}-4 x+8}+\dfrac{2(4-x)^{2}}{x^{2}-4 x+8}=4\),
\(∴C\)正确;
对于\(D\)选项:若函数\(f(x)\)的图象关于\((4 ,4)\)对称,
则\(f(x)+f(8-x)=8\),
而\(f(x)+f(8-x)\)\(=\dfrac{2 x^{2}}{x^{2}-4 x+8}+\dfrac{2(8-x)^{2}}{x^{2}-12 x+40}\)显然不恒等于\(8\),
\(∴D\)错误.
故选\(C\).
\({\color{Red}{方法三 取特殊值排除法}}\)
对于\(A\)选项:\(f(0)=0\),\(f(4)≠0\),故函数\(f(x)\)的图象不可能关于\(x=2\)对称,排除\(A\);
对于\(B\)选项:\(f(0)=0\),\(f(8)≠0\),故函数\(f(x)\)的图象不可能关于\(x=4\)对称,排除\(B\);
对于\(D\)选项:\(f(0)=0\),\(f(8)=\dfrac{16}{5} \neq 8\),故函数\(f(x)\)的图象不可能关于\((4 ,4)\)对称,排除\(D\);
故选\(C\).
【点拨】
① 从三种方法来说,显然大家觉得方法三有种秒杀的感觉,很爽,从应试的角度来讲是这样子的.从提高数学能力的角度,还是需要好好领会下方法一、二;
② 方法一需要理解抽象函数的平移变换:左加右减,上加下减,它充分体现了数形结合的力量;
③ 方法一其实也是方法二的一种特殊情况的表现;
对于函数自身的轴对称和中心对称关系
(1) 轴对称:若\(f(x+a)=f(b-x)\), 则\(y=f(x)\)有对称轴\(x=\dfrac{a+b}{2}\).
对于选项\(A\),令\(a=b=2\),有\(f(x+2)=f(2-x)\),
即证明\(f(x+2)\)是偶函数便可.
(2) 中心对称:若函数\(y=f(x)\)满足条件\(f(a+x)+f(b-x)=c\)(\(a\),\(b\),\(c\)为常数),则函数\(y=f(x)\)的图象关于点\(\left(\dfrac{a+b}{2}, \dfrac{c}{2}\right)\)对称.
对于选项\(C\),令\(a=b=2\),\(c=4\),有\(f(2+x)+f(2-x)=4\)\(\Rightarrow f(2+x)-2=2-f(2-x)\),
即证明\(y=f(2+x)-2\)是奇函数.
【题型三】两个函数图象之间的对称关系
【典题1】 下列函数中,其图象与函数\(y=lgx\)的图象关于点\((1 ,0)\)对称的是( )
A.\(y=\lg(1-x)\) \(\qquad\)B.\(y=\lg(2-x)\)\(\qquad\)C.\(y=\log _{0.1}(1-x)\) \(\qquad\)D.\(y=\log _{0.1}(2-x)\)
【解析】 设所求函数图象上任意一点\(P(x ,y)\),
则\(P(x ,y)\)关于\((1 ,0)\)对称的点\((2-x ,-y)\)在\(y=lgx\)上,即\(-y=lg(2-x)\),
所以\(y=-\lg (2-x)=\log _{0.1}(2-x)\)
故选:\(D\).
【典题2】 下列函数中,其图象与函数\(y=2^x\)的图象关于直线\(y=1\)对称的是\(\underline{\quad \quad }\) .
【解析】 设\(P(x ,y)\)为所求函数图象上的任意一点,
它关于直线\(y=1\)对称的点是\(Q(x ,2-y)\).
由题意知点\(Q(x ,2-y)\)在函数\(y=2^x\)的图象上,
则\(2-y=2^x\),即\(y=2-2^x\).
【点拨】 这种涉及函数对称性、平移去求解析式的题,常用代入法.
巩固练习
1(★★)已知函数\(f(x)=\dfrac{a x+2}{x-6}\)的对称中心为\((b ,1)\),则\(a=\) ;\(b=\) \(\underline{\quad \quad }\).
2(★★)【多选题】函数\(f(x)\)的图象关于直线\(x=1\)对称,那么( )
A.\(f (2-x)=f (x)\) \(\qquad \qquad \qquad \qquad \qquad \qquad\) B.\(f (1-x)=f (1+x)\)
C.函数\(y=f (x+1)\)是偶函数 \(\qquad \qquad \qquad \qquad\) D.函数\(y=f (x-1)\)是偶函数
3(★★★)已知函数\(f(x)=\ln x+\ln(a-x)\)的图象关于直线\(x=1\)对称,则函数\(f(1)\)的值为 ( )
A.\(0\)\(\qquad \qquad \qquad \qquad\) B.\(1\) \(\qquad \qquad \qquad \qquad\)C.\(\ln a\) \(\qquad \qquad \qquad \qquad\)D.\(-1\)
4(★★★)已知函数\(f(x)=\ln \dfrac{x}{4-x}\),则( )
A.\(y=f(x)\)的图象关于点\((2 ,0)\)对称
B.\(y=f(x)\)的图象关于直线\(x=2\)对称
C.\(f(x)\)在\((0 ,4)\)上单调递减
D.\(f(x)\)在\((0 ,2)\)上单调递减,在\((2 ,4)\)上单调递增
5(★★)同一平面直角坐标系中,函数\(y=2^{x+1}\)与\(y=2^{1-x}\)的图象( )
A.关于原点对称 \(\qquad \qquad\) B.关于\(x\)轴对称 \(\qquad \qquad\) C.关于\(y\)轴对称 \(\qquad \qquad\) D.关于直线\(y=x\)对称
6(★★★)【多选题】已知定义在\(R\)上的函数\(y=f(x)\)满足条件\(f(x+2)=-f(x)\),且函数\(y=f(x-1)\)为奇函数,则( )
A.函数\(y=f(x)\)是周期函数
B.函数\(y=f(x)\)的图象关于点\((-1 ,0)\)对称
C.函数\(y=f(x)\)为\(R\)上的偶函数
D.函数\(y=f(x)\)为\(R\)上的单调函数
答案
1.\(1,6\)
2.\(ABC\)
3.\(A\)
4.\(A\)
5.\(C\)
6.\(ABC\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号