3.3 函数的奇偶性
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步拔高练习,难度3颗星!
模块导图
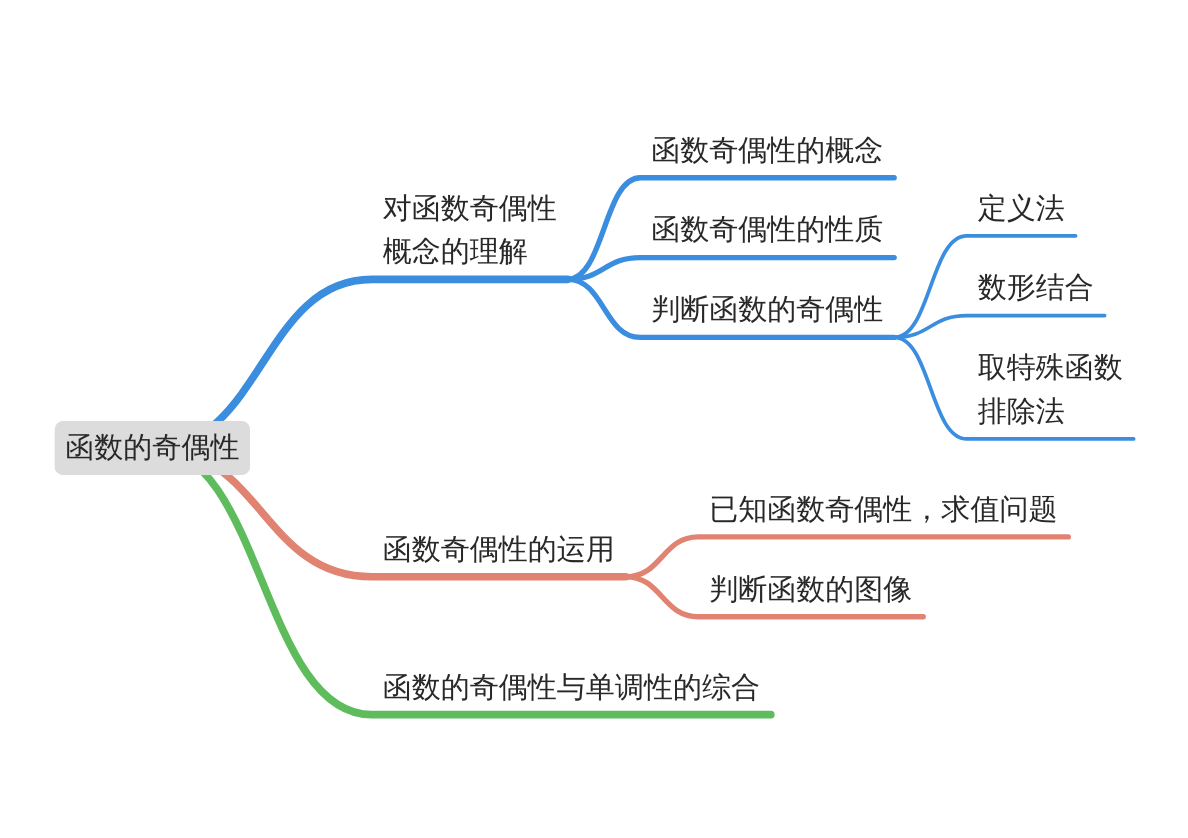
知识剖析
函数奇偶性的概念
① 一般地,设函数\(f(x)\)的定义域为\(I\),如果\(∀x∈I\),都有\(-x∈I\),且\(f(-x)=f(x)\),那么函数\(f(x)\)就叫做偶函数.
② 一般地,设函数\(f(x)\)的定义域为\(I\),如果\(∀x∈I\),都有\(-x∈I\),且\(f(-x)=-f(x)\),那么函数\(f(x)\)就叫做奇函数.
由奇偶函数的概念可知道其定义域\(I\)是关于原点对称的.
性质
① 偶函数关于\(y\)轴对称;
② 奇函数关于原点对称;
③ 若奇函数\(f(x)\)定义域内含有\(0\),则\(f(0)=0\);
④ 在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.
判断函数奇偶性的方法
① 定义法
先判断定义域是否关于原点对称,再求\(f(-x)\), 看下与\(f(x)\)的关系:若\(f(-x)=f(x)\),则\(y=f(x)\)是偶函数;若\(f(-x)=-f(x)\),则\(y=f(x)\)是奇函数.
② 数形结合
若函数关于原点对称,则函数是奇函数;若函数关于\(y\)轴对称,则函数是偶函数.
③ 取特殊值排除法(选择题)
比如:若根据函数得到\(f(1)≠f(-1)\),则排除\(f(x)\)是偶函数.
④ 性质法
偶函数的和、差、积、商(分母不为\(0\))仍为偶函数;奇函数的和、差 (分母不为\(0\))仍为奇函数;
奇(偶)数个奇函数的积为奇(偶)函数;两个奇函数的商(分母不为\(0\))为偶函数;
一个奇函数与偶函数的积为奇函数.
对于复合函数\(F(x)=f(g(x))\)的奇偶性如下图
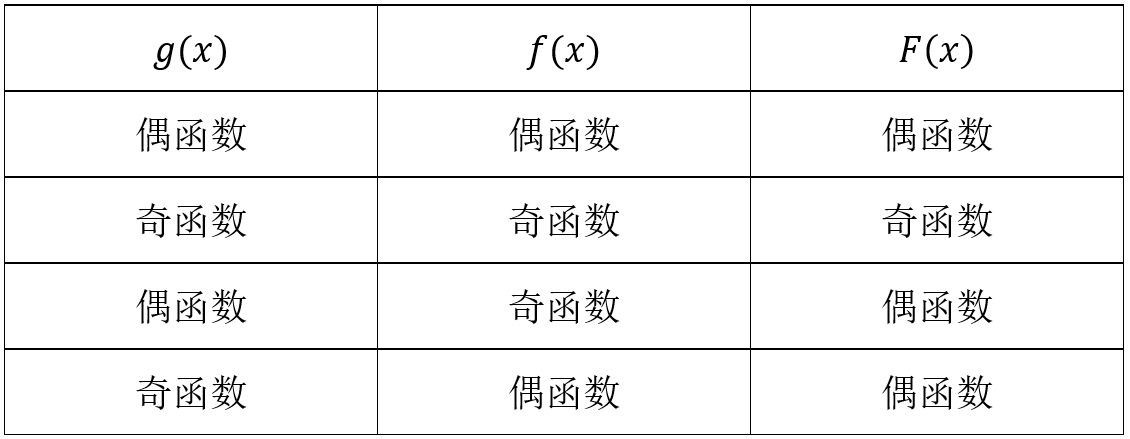
经典例题
【题型一】对函数奇偶性概念的理解
角度1 函数奇偶性的概念
【典题1】 已知\(f(x)=ax^2+bx\)是定义在\([a-1 ,2a]\)上的偶函数,那么\(a+b\)的值是\(\underline{\quad \quad }\).
【解析】 依题意得\(f(-x)=f(x)\),\(∴b=0\),
又\(a-1=-2a\)\({\color{Red}{(奇偶函数的定义域关于原点对称) }}\)
\(\therefore a=\dfrac{1}{3}\),\(\therefore a+b=\dfrac{1}{3}\).
【典题2】 \(f(x)\)是定义在\(R\)上的奇函数,下列结论中,不正确的是________:
\((1)f(-x)+f(x)=0\)
\((2)f(-x)-f(x)=-2 f(x)\)
\((3)f(x)⋅f(-x)≤0\)
\((4) f(x)/f(-x) =-1\)
【解析】 根据奇函数的定义可知\(f(-x)=-f(x)\),则\((1)\),\((2)\)正确;
对于\((3)\),\(f(x)f(-x)=-f^2 (x)≤0\), 故正确;
对于\((4)\),\(f(x)\)是定义在\(R\)上的奇函数,则\(f(0)=0\), 则\((4)\)不正确,
故答案为:\((4)\).
角度2 判断函数的奇偶性
\({\color{Red}{情况1\quad 具体函数的奇偶性判断}}\)
【典题1】 函数\(f(x)=\dfrac{\sqrt{4-x^{2}}}{|x+3|-3}\)的图象关于\(\underline{\quad \quad }\)对称.
【解析】 要使函数有意义,
则\(\left\{\begin{array}{c}
4-x^{2} \geq 0 \\
|x+3|-3 \neq 0
\end{array}\right.\),
解得\(-2<x<0\)或\(0<x<2\),
则定义域关于原点对称.
此时\(|x+3|=x+3\),
则函数\(f(x)=\dfrac{\sqrt{4-x^{2}}}{|x+3|-3}=\dfrac{\sqrt{4-x^{2}}}{x+3-3}=\dfrac{\sqrt{4-x^{2}}}{x}\)
\({\color{Red}{(化简函数形式很重要)}}\)
\(\because f(-x)=-\dfrac{\sqrt{4-x^{2}}}{x}=-f(x)\),
\(∴\)函数\(f(x)\)是奇函数,图象关于原点对称,
【点拨】 本题利用定义法判断函数的奇偶性,首先判断定义域是否关于原点对称,这点很重要;
\({\color{Red}{情况2 \quad 抽象函数的奇偶性判断}}\)
【典题1】 设\(f(x)\)是\(R\)上的任意函数,则下列叙述正确的是( )
A.\(f(x) f(-x)\)是奇函数 \(\qquad \qquad \qquad \qquad\) B.\(f(x) |f(-x)|\)是奇函数
C.\(f(x)- f(-x)\)是奇函数 \(\qquad \qquad \qquad \qquad\) D.\(f(x) +f(-x)\)是奇函数
【解析】 \({\color{Red}{方法一\quad 定义法}}\)
\(A\)选项:设\(F(x)=f(x)f(-x)\),
则\(F(-x)=F(x)\)为偶函数.
\(B\)选项:设\(G(x)=f(x)|f(-x)|\),
则\(G(-x)=f(-x)|f(x)|\).
\(∴G(x)\)与\(G(-x)\)关系不定.
\(C\)选项:设\(M(x)=f(x)-f(-x)\),
\(∴M(-x)=f(-x)-f(x)=-M(x)\),
\(∴M(x)\)为奇函数.
\(D\)选项:设\(N(x)=f(x)+f(-x)\),
则\(N(-x)=f(-x)+f(x)\),\(∴N(x)\)为偶函数.
故选\(C\).
\({\color{Red}{方法二 \quad 取特殊函数排除法}}\)
令\(f(x)=x\),可知\(F(x)=f(x)f(-x)=x^2\)是偶函数,排除\(A\),
令\(f(x)=x^2\),可知\(F(x)=f(x)|f(-x)|=x^4\)是偶函数,排除\(B\),
可知\(N(x)=f(x)+f(-x)=2x^2\)是偶函数,排除\(D\).
故选\(C\).
【点拨】
① 判断函数的奇偶性,一般利用定义法:先判断定义域是否关于原点对称,再求\(f(-x)\),看下与\(f(x)\)的关系.偶尔结合函数图像也可以.
② 判断抽象函数的奇偶性时,可以通过“取特殊函数排除法”.
③ 一般情况下,奇函数+奇函数=奇函数,偶函数+偶函数=偶函数,奇函数×奇函数=偶函数,偶函数×偶函数=偶函数.
巩固练习
1(★)下列函数中,是偶函数的是( )
A.\(y=|x^2+x|\)\(\qquad \qquad\) B.\(y=2^{|x|}\) \(\qquad \qquad\) C.\(y=x^3+x\) \(\qquad \qquad\) D.\(y=lgx\)
2(★)函数\(f(x)=\dfrac{9^{x}+1}{3^{x}}\)的图象关于( )对称
A.原点 \(\qquad \qquad \qquad \qquad\) B.\(y=x\) \(\qquad \qquad \qquad \qquad\) C.\(x\)轴 \(\qquad \qquad \qquad \qquad\) D.\(y\)轴
3(★★)若函数\(f(x)\)的定义域是\(R\),且对任意\(x\),\(y∈R\),都有\(f(x+y)=f(x)+f(y)\)成立.试判断\(f(x)\)的奇偶性.
参考答案
1.\(B\)
2.\(D\)
3.奇函数
【题型二】函数奇偶性的运用
角度1 已知函数奇偶性,求值问题
【典题1】 设\(f(x)\)为定义上\(R\)上的奇函数,当\(x≥ 0\)时,\(f(x)=2^x+2x+b\)(\(b\)为常数),求\(f(-1)\).
【解析】 因为\(f(x)\)为定义在\(R\)上的奇函数,
所以\(f(0)=0⇒2^0+2×0+b=0\),
解得\(b=-1\),
所以当\(x≥0\)时,\(f(x)=2^x+2x-1\),
又因为\(f(x)\)为定义在\(R\)上的奇函数,
所以\(f(-1)=-f(1)=-(2^1+2× 1-1)=-3\),故选\(A\).
【点拨】 若奇函数\(y=f(x)\)定义域内为\(I\),且\(0∈I\),则有\(f(0)=0\).
【典题2】 若函数\(F(x)=f(x)-2x^4\)是奇函数,\(G(x)=f(x)+\left(\dfrac{1}{2}\right)^{x}\)为偶函数,
则\(f(-1)=\)\(\underline{\quad \quad }\).
【解析】 \(∵\)函数\(F(x)=f(x)-2x^4\)是奇函数,
\(∴F(1)+F(-1)=0\),
即\(f(1)-2+f(-1)-2=0\),
则\(f(1)+f(-1)=4\)①,
\(∵G(x)=f(x)+\left(\dfrac{1}{2}\right)^{x}\)为偶函数,
\(∴G(1)=G(-1)\),即\(f(1)+\dfrac{1}{2}=f(-1)+2\),
则\(f(1)-f(-1)=\dfrac{3}{2}\)②,
由①-②解得\(f(-1)=\dfrac{4-\dfrac{3}{2}}{2}=\dfrac{5}{4}\).
角度2 判断函数的图像
【典题1】 函数\(f(x)=\dfrac{x^{3}}{2^{-x}-2^{x}}\)的图象大致为( )
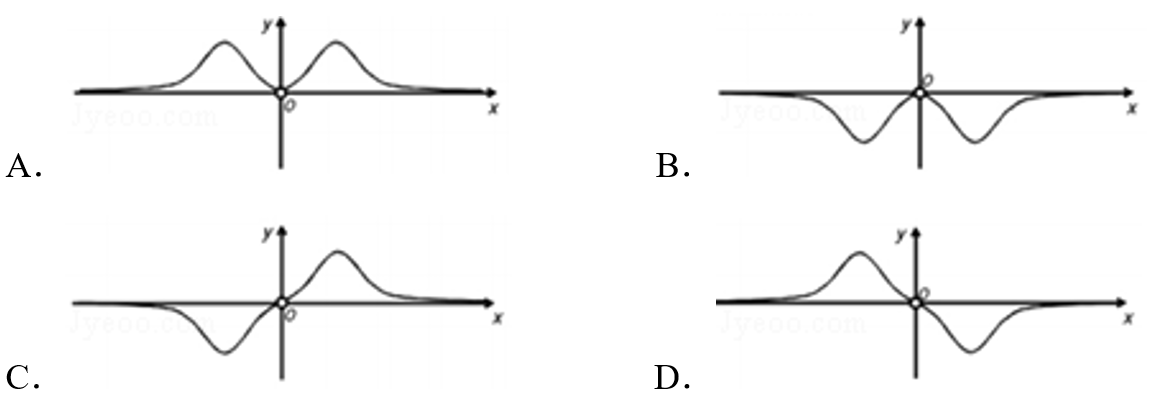
【解析】 函数的定义域为\(\{x|x≠0\}\)关于原点对称,
且\(f(-x)=\dfrac{-x^{3}}{2^{x}-2^{-x}}=\dfrac{x^{3}}{2^{-x}-2^{x}}=f(x)\),
\({\color{Red}{(或由y=x^3,y=2^{-x}-2^x均是奇函数,得f(x)=\dfrac{x^{3}}{2^{-x}-2^{x}}是偶函数)}}\)
即函数\(f(x)\)为偶函数,其图象关于\(y\)轴对称,可排除\(CD\);
又\(f(1)=\dfrac{1}{2^{-1}-2}=-\dfrac{2}{3}<0\),可排除\(A\);
故选:\(B\).
【点拨】 选择题中判断函数的图像,可采取排除法,主要是研究函数性质(定义域、值域、奇偶性、单调性等)、取特殊值等手段进行排除选项!其中取特殊值排除法最简单.
巩固练习
1(★)若函数\(f(x)=\dfrac{2^{x}-a}{2^{x}+1}\)的图象关于\(y\)轴对称,则常数\(a=\)\(\underline{\quad \quad }\) .
2(★)已知函数\(f(x)=x^5-ax^3+bx+2\),\(f(-5)=17\),则\(f(5)\)的值是\(\underline{\quad \quad }\).
3(★★)已知函数\(f(x)=g(x+1)-2^x\)为定义在\(R\)上的奇函数,则\(g(0)+g(1)+g(2)=\)\(\underline{\quad \quad }\).
4(★★)函数\(f(x)=\dfrac{\left(3^{x}-1\right) \ln x^{2}}{3^{x}+1}\)的部分图象大致为 ( )
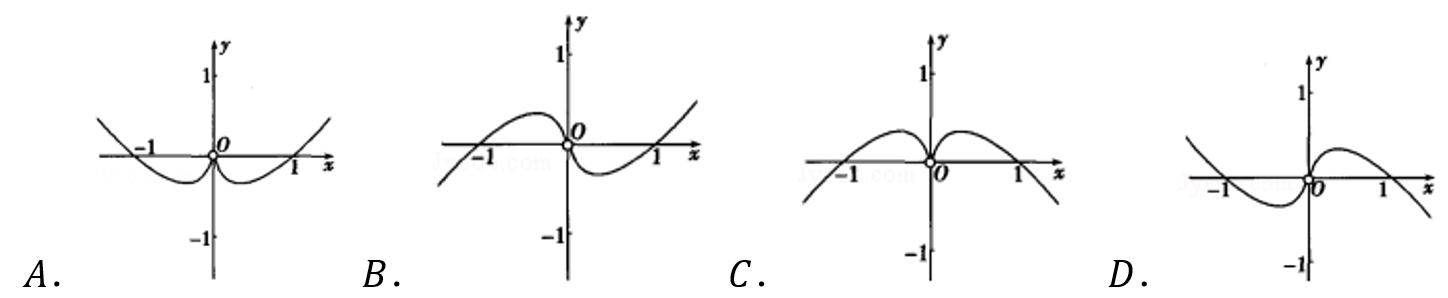
参考答案
1.\(-1\)
2.\(-13\)
3.\(\dfrac{7}{2}\)
4.\(B\)
【题型三】函数的奇偶性与单调性的综合
【典题1】 已知奇函数\(y=f(x)\)在\((-∞ ,0)\)为减函数,且\(f(2)=0\),则不等式
\((x-1)f(x-1)>0\)的解集为 ( )
A.\(\{x \mid-3<x<-1\}\)
B.\(\{x \mid-3<x<1 \text { 或 } x>2\}\)
C.\(\{x \mid-3<x<0 \text { 或 } x>3\}\)
D.\(\{x \mid-1<x<1 \text { 或 } 1<x<3\}\)
【解析】 由题意画出\(f(x)\)的草图如下,
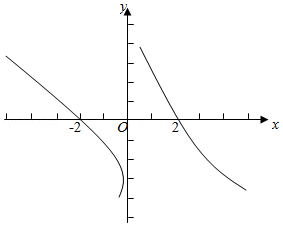
因为\((x-1)f(x-1)>0\),所以\((x-1)\)与\(f(x-1)\)同号,
由图象可得\(-2<x-1<0\)或\(0<x-1<2\),
解得\(-1<x<1\)或\(1<x<3\),
故选:\(D\).
【点拨】 涉及到函数奇偶性和单调性综合的题目,多利用数形结合的方法进行理解,对每个条件要等价转化,做到有根有据的,不能“想当然”.
【典题2】 设函数\(f(x)=lg(x^2+1)\),则使得\(f(3x-2)>f(x-4)\)成立的\(x\)的取值范围为( )
A.\(\left(\dfrac{1}{3}, 1\right)\) \(\qquad \qquad\) B.\(\left(-1, \dfrac{3}{2}\right)\) \(\qquad \qquad\) C.\(\left(-\infty, \dfrac{3}{2}\right)\) \(\qquad \qquad\) D.\((-\infty,-1) \cup\left(\dfrac{3}{2},+\infty\right)\)
【解析】 \({\color{Red}{方法一}}\)
\(∵f(x)=lg(x^2+1)\)
\(∴\)由\(f(3x-2)>f(x-4)\)
得\(lg[(3x-2)^2+1]>lg[(x-4)^2+1]\),\({\color{Red}{(代入原函数暴力求解)}}\)
则\((3x-2)^2+1>(x-4)^2+1\),
解得\(x<-1\)或\(x>\dfrac{3}{2}\).
\({\color{Red}{方法二}}\)
根据题意,函数\(f(x)=lg(x^2+1)\),其定义域为\(R\),
有\(f(-x)=lg(x^2+1)=f(x)\),
即函数\(f(x)\)为偶函数,
设\(t=x^2+1\),则\(y=lgt\),
在区间\([0 ,+∞)\)上,\(t=x^2+1\)为增函数且\(t≥1\),\(y=lgt\)在区间\([1 ,+∞)\)上为增函数,
则\(f(x)=lg(x^2+1)\)在\([0 ,+∞)\)上为增函数,
\(f(3x-2)>f(x-4)\)\(⇒f(|3x-2|)>f(|x-4|)\)\(⇒|3x-2|>|x-4|\),
解得\(x<-1\)或\(x>\dfrac{3}{2}\),
故选:\(D\).
【点拨】
① 若函数\(y=f(x)\)是偶函数,则函数在\(y\)轴两侧的单调性是相反的,
若函数\(y=f(x)\)是奇函数,则函数在\(y\)轴两侧的单调性是相同的,
② 若函数\(y=f(x)\)是偶函数,在\([0 ,+∞)\)上递增,
则求解\(f(x_2)>f(x_1)\)等价于解不等式\(|x_2 |>|x_1 |\),不要漏了绝对值.(如下图所示).

③ 遇到类似\(f(3x-2)>f(x-4)\)的函数不等式,一般都是利用函数的单调性处理.
巩固练习
1(★)下列函数中,既是偶函数,又在\((0,+∞)\)上单调递增的是( )
A.\(f(x)=1-x^2\)\(\qquad \qquad\) B.\(f(x)=x-\dfrac{1}{x}\)\(\qquad \qquad\)C.\(f(x)=\log _{\frac{1}{2}}|x|\) \(\qquad \qquad\)D.\(f(x)=2^{|x|}\)
2(★)如果奇函数\(f(x)\)在区间\([1 ,5]\)上是减函数,且最小值为\(6\),那么\(f(x)\)在区间\([-5 ,-1]\)上是 ( )
A.减函数且最大值为\(-6\) \(\qquad \qquad \qquad\) B.增函数且最大值为\(6\)
C.减函数且最小值为\(-6\) \(\qquad \qquad \qquad\) D.增函数且最小值为\(-6\)
3(★★)已知函数\(f(x)=x^3+2x\),则不等式\(f(2x)+f(x-1)>0\)的解集为\(\underline{\quad \quad }\) .
4(★★)已知函数\(f(x)=ln|x|+x^2\),设\(a=f(-2)\),\(b=f(1)\),\(c=f(2^{0.3})\),则\(a,c,b\)的大小关系\(\underline{\quad \quad }\).
5(★★★)已知\(f(x)\)是\(R\)上的奇函数且单调递增,则下列函数是偶函数且在\((0 ,+∞)\)上单调递增的有\(\underline{\quad \quad }\).
①\(y=|f(x)|\);②\(y=f(x^2+x)\);
③\(y=f(|x|)\);④\(y=e^{f(x)} +e^{-f(x)}\).
参考答案
1.\(D\)
2.\(A\)
3.\(\left(\dfrac{1}{3},+\infty\right)\)
4.\(a>c>b\)
5.①③④


 浙公网安备 33010602011771号
浙公网安备 33010602011771号