3.2 函数的单调性

\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步拔高练习，难度3颗星！

模块导图

知识剖析

函数单调性的概念

一般地，设函数\(y=f(x)\)的定义域为\(I\)，区间\(D∈I\):
如果\(∀x_1\),\(x_2∈D\)，当\(x_1<x_2\)时，都有\(f(x_1)<f(x_2)\)，那么就说\(f(x)\)在区间\(D\)上单调递增(图①).特别地，当函数\(f(x)\)在它定义域上单调递增时，我们就称它是增函数.
如果\(∀x_1\),\(x_2∈D\)，当\(x_1<x_2\)时，都有\(f(x_1 )>f(x_2)\)，那么就说\(f(x)\)在区间\(D\)上单调递减(图②).特别地，当函数\(f(x)\)在它定义域上单调递减时，我们就称它是减函数.

\({\color{Red}{ Eg }}\) \(y=\dfrac{1}{x}\)在\((0,+∞)\)上单调递减，但它不是减函数，
特别注意它的减区间是\((0,+∞)\)，\((-∞,0)\)，不是\((0,+∞)∪(-∞,0)\).
 

单调性概念的拓展

① 若\(y=f(x)\)递增，\(x_2>x_1\)，则\(f(x_2 )>f(x_1)\).
\({\color{Red}{ Eg }}\) \(y=f(x)\)递增，则\(f(a^2 )≥f(0)\).
② 若\(y=f(x)\)递增，\(f(x_2 )≥f(x_1)\)，则\(x_2≥x_1\).
\({\color{Red}{ Eg }}\) \(y=f(x)\)递增 ,\(f(1-m)≥f(n)\), 则\(1-m≥n\).
\(y=f(x)\)递减，有类似结论！
 

判断函数单调性的方法

\({\color{Red}{①\quad 定义法 }}\)
解题步骤
\((1)\)任取\(x_1\),\(x_2∈D\)，且\(x_1<x_2\)；
\((2)\)作差\(f(x_1)－f(x_2)\)；
\((3)\)变形(通常是因式分解和配方)；
\((4)\)定号(即判断差\(f(x_1)－f(x_2)\)的正负)；
\((5)\)下结论(指出函数\(f(x)\)在给定的区间\(D\)上的单调性)．

\({\color{Red}{ ②\quad 数形结合}}\)

\({\color{Red}{ ③\quad 性质法}}\)
增函数+增函数=增函数，减函数+减函数=减函数；
但增函数×增函数不一定是增函数，比如\(y=x\)，\(y=x-2\)均是增函数，而\(y=x(x-2)\)不是.

\({\color{Red}{④ \quad复合函数的单调性 }}\)
\((1)\)如果\(y=f(u)(u∈M)\),\(u=g(x)(x∈A)\), 则\(y=f[g(x)]=F(x)\)\((x∈A)\)称为\(f\)、\(g\)的复合函数；
\({\color{Red}{ Eg }}\)\(F(x)=\dfrac{1}{x^{2}+x}\)(\(f(u)=\dfrac{1}{u}\)和\(g(x)= x^2+x\)的复合函数)；
\(F(x)=\sqrt{1-2 x}\)(\(f(u)=\sqrt{u}\)和\(g(x)= 1-2x\)的复合函数)；
\(F(x)=2^{\frac{1}{x}}\)(\(f(u)=2^u\)和\(g(x)=\dfrac{1}{x}\)的复合函数).

\((2)\)同增异减
设函数\(u=g(x)(x∈A)\)的值域是\(M\)，函数\(y=f(u)(u∈M)\),
若\(y=f(u)\)，\(u=g(x)\)在各自区间单调性相同，则复合函数\(y=f[g(x)]\)在区间\(A\)上递增；
若\(y=f(u)\),\(u=g(x)\)在各自区间单调性不同，则复合函数\(y=f[g(x)]\)在区间A上递减.
 

函数的最值

一般地，设函数\(y=f(x)\)的定义域为\(I\)，如果存在实数\(M\)满足：
\((1)\)\(∀x∈I\)，都有\(f(x)≤M\)；
\((2)\)\(∃x_0∈I\)，使得\(f(x_0 )=M\)；
那么，我们称\(M\)是函数\(y=f(x)\)的最大值.(最小值类似定义)
简单来说，最大值和最小值分别是函数图像中最高点和最低点的函数值.
 

经典例题

【题型一】对函数单调性的理解

【典题1】 函数\(y=f(x)\)在\(R\)是增函数，若\(a+b≤ 0\)，则有 (　　)
A.\(f(a)+f(b)≤-f(a)-f(b)\)
B.\(f(a)+f(b)≥-f(a)-f(b)\)
C.\(f(a)+f(b)≤ f(-a)+f(-b)\)
D.\(f(a)+f(b)>f(-a)+f(-b)\)
【解析】\(∵a＋b≤0\),
\(∴a≤-b\),\(b≤-a\)
又\(∵\)函数\(f(x)\)在\(R\)上是增函数，
\(∴f(a)≤f(-b)\),\(f(b)≤f(-a)\)．
\(∴f(a)＋f(b)≤f(-a)＋f(－b)\)．
故选\(C\).
 

【典题2】 已知函数\(f(x)\)在\(R\)上是单调函数，且对任意\(x∈R\)，都有\(f(f(x)-2^x)=3\)，
则\(f(3)\)的值等于\(\underline{\quad \quad }\)
【解析】\(∵\)函数\(f(x)\)在\(R\)上是单调函数
\(∴\)可设\(f(x)-2^x=t\)(\(t\)是个常数)，
则\(f(x)=2^x+t\)；
\(∴f(t)=2^t+t=3\)；
\(∵f(t)\)在\(R\)上单调递增，
\(∴\)只有\(t=1\)时对应的函数值是\(3\)，即\(f(1)=3\)；
\(∴f(x)=2^x+1\)；
\(∴f(3)=9\)．
【点拨】函数若是单调函数，即函数是“一一对应”的关系，一个\(x\)对应一个\(y\)，所以题目中“\(f(x)-2^x\)”只能是个常数.
 

巩固练习

1(★★)设\(a∈R\)，函数\(f(x)\)在区间\((0 ,+∞)\)上是增函数，则(　　)
A．\(f\left(a^{2}+a+2\right)>f\left(\dfrac{7}{4}\right)\)
B．\(f\left(a^{2}+a+2\right)<f\left(\dfrac{7}{4}\right)\)
C．\(f\left(a^{2}+a+2\right) \geq f\left(\dfrac{7}{4}\right)\)
D．\(f\left(a^{2}+a+2\right) \leq f\left(\dfrac{7}{4}\right)\)
 

2(★★)已知\(f(x)\)是定义在\([0 ,+∞)\)上单调递增的函数，则满足\(f(2 x-1)<f\left(\dfrac{1}{3}\right)\)的\(x\)取值范围是\(\underline{\quad \quad }\)
 

参考答案

1.\(C\)
2.\(\left[\dfrac{1}{2}, \dfrac{2}{3}\right)\)
 

【题型二】 判断函数单调性的方法

方法1 定义法

【典题1】 判断\(f(x)=x+\dfrac{4}{x}\)在\((0 ,2)\),\((2 ,+∞)\)的单调性.
【解析】设\(0<x_1<x_2\),
则\(y_{1}-y_{2}=\left(x_{1}+\dfrac{4}{x_{1}}\right)-\left(x_{2}+\dfrac{4}{x_{2}}\right)\)\(=\left(x_{1}-x_{2}\right)+\left(\dfrac{4}{x_{1}}-\dfrac{4}{x_{2}}\right)\)
\({\color{Red}{(因式分解方便判断差y_1-y_2的正负) }}\)
(1) 假如\(0<x_1<x_2<2\),
则\(0<x_{1} x_{2}<4\)\(\Rightarrow \dfrac{4}{x_{1} x_{2}}>1 \Rightarrow 1-\dfrac{4}{x_{1} x_{2}}<0\),
又\(x_1-x_2<0\),
所以\(y_1-y_2>0 ⇒ y_1>y_2\),
故函数单调递减；
(2) 假如\(2<x_1<x_2\),
则\(x_{1} x_{2}>4 \Rightarrow \dfrac{4}{x_{1} x_{2}}<1\)\(\Rightarrow 1-\dfrac{4}{x_{1} x_{2}}>0\),
又\(x_1-x_2<0\),
所以\(y_1-y_2<0⇒ y_1<y_2\),
故函数单调递增；
所以函数在\((0 ,2)\)内单调递减，在\((2 ,＋∞)\)内单调递增．
【点拨】利用定义法证明函数的单调性，注意熟练掌握解题的步骤：设元—作差—变式—定号—下结论.
 

方法2 数形结合

【典题2】 函数\(f(x)=\dfrac{x}{1-x}\)的单调增区间是 (　　)
A.\((-∞ ,1)\)
B .\((-∞ ,1)∪(1 ,+∞)\)
C .\((-∞ ,1)\),\((1 ,+∞)\)
D .\((-∞ ,-1)\),\((-1 ,+∞)\)
【解析】\(f(x)=\dfrac{-(1-x)+1}{1-x}\)\(=-1+\dfrac{1}{1-x}=-\dfrac{1}{x-1}-1\);
\({\color{Red}{ (分离常数法) }}\)
\(∴f(x)\)的图象是由\(y=-\dfrac{1}{x}\)的图象沿\(x\)轴向右平移\(1\)个单位，然后沿\(y\)轴向下平移\(1\)个单位得到, 如下图

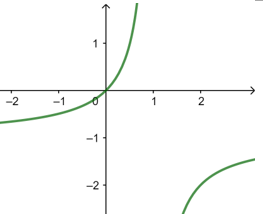
\(∴f(x)\)的单调增区间是\((-∞ ,1)\),\((1 ,+∞)\)．
故选\(C\)． \({\color{Red}{(切勿选B) }}\)
【点拨】
① 本题先利用分离常数法，再利用函数的平移变换得到函数的图像从而得到函数单调性.
② 利用数形结合的方法，平时需要多注意函数图像的变换，包括平移变换、对称变换、翻转变换等.
 

方法3 复合函数的单调性

【典题3】 函数\(f(x)=\sqrt{x^{2}+4 x-12}\)的单调减区间为\(\underline{\quad \quad }\).
【解析】函数\(f(x)=\sqrt{x^{2}+4 x-12}\)是由函数\(f(u)=\sqrt{u}\)和\(u(x)=x^2+4 x-12\)组成的复合函数，
\(∵x^2+4 x-12≥0\),
\(∴\)函数\(y=f(x)\)的定义域是\(x≤-6\)或\(x≥2\)
\({\color{Red}{(优先考虑定义域，否则容易选B) }}\)
由二次函数图像易得\(u(x)=x^2+4 x-12\)在\((-∞ ,-6]\)单调递减，在\([2 ,＋∞)\)单调递增，
而\(f(u)=\sqrt{u}\)在\(u≥0\)是单调递增，
由复合函数单调性的“同增异减”，
可得函数\(f(x)\)的单调减区间\((-∞,-6]\)．
【点拨】
① 研究函数的基本性质，优先考虑定义域；
② 研究复合函数，要弄清楚它由什么函数复合而成的.
 

巩固练习

1(★)下列四个函数在\((-∞,0)\)是增函数的为(　　)
A．\(f(x)=x^2+4\) \(\qquad\)B．\(f(x)=1-2x\) \(\qquad\)C．\(f(x)=-x^2-x+1\) \(\qquad\)D．\(f(x)=2-\dfrac{3}{x}\)
 

2(★)设函数\(f(x)\)在\(R\)上为增函数，则下列结论一定正确的是(　　)
A．\(y=\dfrac{1}{f(x)}\)在\(R\)上为减函数 \(\qquad \qquad \qquad\) B．\(y=|f(x)|\)在\(R\)上为增函数
C．\(y=-\dfrac{1}{f(x)}\)在\(R\)上为增函数 \(\qquad \qquad \qquad\) D．\(y=-f(x)\)在\(R\)上为减函数
 

3(★)函数\(f(x)=x|x-2|\)的递减区间为\(\underline{\quad \quad }\)．
 

4(★)函数\(y=\sqrt{x^{2}+3 x}\)的单调递减区间为\(\underline{\quad \quad }\)．
 

5(★★)函数\(f(x)=\left|\left(\dfrac{1}{2}\right)^{x}-2\right|\)的单调递增区间为\(\underline{\quad \quad }\)．
 

6(★★★)已知函数\(f(x)=x-\dfrac{a}{x}\)在定义域\([1,20]\)上单调递增
(1)求\(a\)的取值范围；
(2)若方程\(f(x)=10\)存在整数解，求满足条件\(a\)的个数.
 
 

7(★★★)函数\(f(x)\),\(g(x)\)在区间\([a ,b]\)上都有意义，且在此区间上
①\(f(x)\)为增函数，\(f(x)>0\)；
②\(g(x)\)为减函数，\(g(x)<0\)．
判断\(f(x)g(x)\)在\([a ,b]\)的单调性，并给出证明．
 
 

参考答案

1.\(D\)
2.\(D\)
3.\((1 ,2)\)
4.\((-∞ ,-3]\)
5.\([-1,+∞)\)
6.\((1)a≥-1\)\((2)11\)个
7. 提示：定义法
 

【题型三】函数单调性的应用

角度1 解不等式

【典题1】 已知函数\(f(x)=\left(\dfrac{1}{2}\right)^{x}-x^{3}\)，若\(f(2a+1)>f(a-1)\)，则实数\(a\)的取值范围是\(\underline{\quad \quad }\) .
【解析】\(\because y=\left(\dfrac{1}{2}\right)^{x}\)和\(y=-x^3\)在\(R\)上都单调递减，
\(\therefore f(x)=\left(\dfrac{1}{2}\right)^{x}-x^{3}\)在\(R\)上都单调递减，
\(∴\)由\(f(2a+1)>f(a-1)\)得\(2a+1<a-1\)，
解得\(a<-2\)．
【点拨】
① 我们有增函数+增函数=增函数，减函数+减函数=减函数，由此性质求出函数单调性.
② 处理类似“\(f(2a+1)>f(a-1)\)”这样的不等式，可利用函数的单调性去掉\(“f"\)求解，不要硬代入原函数来个“暴力求解”，特别\(f(x)\)是复杂的函数或者抽象函数的时候.
 

角度2 求参数取值范围或值

【典题2】 若\(f(x)=\left\{\begin{array}{l} a x^{2}+1, x \geq 0 \\ \left(a^{2}-1\right) \cdot 2^{a x}, x<0 \end{array}\right.\)\((a \neq 1)\)，在定义域\((-∞ ,+∞)\)上是单调函数，则\(a\)的取值范围\(\underline{\quad \quad }\).
【解析】\(f(x)\)在定义域\((-∞ ,+∞)\)上是单调函数，
①函数的单调性是增函数时，可得当\(x=0\)时，\((a^2-1)\cdot 2^{ax}≤ax^2+1=1\),
即\(a^2-1≤1\)，解之得\(-\sqrt{2} \leq a \leq \sqrt{2}\)，
\(∵x≥0\)时，\(y=ax^2+1\)是增函数，
\(∴a>0\)
\(∵x<0\)时，\((a^2-1)\cdot 2^{ax}\)是增函数，
\(∴a^2-1>0\)，得\(a<-1\)或\(a>1\)，
综上实数\(a\)的取值范围是\(1<a \leq \sqrt{2}\)；
②函数的单调性是减函数时，
可得当\(x=0\)时，\((a^2-1)\cdot 2^{ax}≥ax^2+1=1\)，
即\(a^2-1≥1\)，解之得\(a \leq-\sqrt{2}\)或\(a \geq \sqrt{2}\)，
\(∵x≥0\)时，\(y=ax^2+1\)是减函数，
\(∴a<0\)
又\(∵x<0\)时，\((a^2-1)\cdot 2^{ax}\)是减函数，
\(∴a^2-1>0\)，得\(a<-1\)或\(a>1\)
综上实数\(a\)的取值范围是\(a \leq-\sqrt{2}\)；
综上所述，得\(a \in(-\infty,-\sqrt{2}] \cup(1, \sqrt{2}]\).
【点拨】遇到分段函数，注意分离讨论和数形结合“双管齐下”方能一击制敌.
 

角度3 求函数最值

【典题3】 已知函数\(f(x)=ax^2-|x-a|\)．
(1)当\(a=1\)时，求\(f(x)\)的值域；
(2)当\(a>0\)时，求函数\(f(x)\)在区间\([0,+∞)\)上的最小值．
【解析】(1)\(a=1\)时，\(f(x)=x^{2}-|x-1|=\left\{\begin{array}{l} x^{2}-x+1, x \geq 1 \\ x^{2}+x-1, x<1 \end{array}\right.\)
\({\color{Red}{(遇到绝对值可变成分段函数处理) }}\)
\(∵f(x)\)在\(\left(-\infty,-\dfrac{1}{2}\right)\)上递减，在\(\left(-\dfrac{1}{2},+\infty\right)\)上递增，
\(\therefore f(x) \geq f\left(-\dfrac{1}{2}\right)=-\dfrac{5}{4},\)，
\(∴f(x)\)值域为\(\left[-\dfrac{5}{4},+\infty\right)\)．
(2)\(f(x)=a x^{2}-|x-a|=\left\{\begin{array}{l} a x^{2}-x+a, x \geq a \\ a x^{2}+x-a, x<a \end{array}\right.\)，
①当\(x<a\)时，\(f(x)=ax^2+x-a\)，对称轴\(x=-\dfrac{1}{2 a}<0\)，
\(∴f(x)\)在\([0 ,a]\)单调递增，
\(∴f(x)≥f(0)=-a\)．
②当\(x≥a\)时，\(f(x)=ax^2-x+a\)，对称轴\(x=\dfrac{1}{2 a}>0\)，
\({\color{Red}{(对于分段函数，多结合图像进行分析，比较对称轴x=\dfrac{1}{2 a}与a的大小)}}\)
\((i)\)当\(\dfrac{1}{2 a} \leq a\)即\(a \geq \dfrac{\sqrt{2}}{2}\)时，\(f(x)\)在\([a ,+∞)\)单调递增，
\(∴f(x)≥f(a)=a^3>f(0)=-a\)，
\(∴f(x)_{min}=f(0)=-a\)．
\((ii)\)当\(\dfrac{1}{2 a}>a\)，即\(0<a<\dfrac{\sqrt{2}}{2}\)时，
\(f(x)\)在\(\left[a, \dfrac{1}{2 a}\right)\)单调递减，在\(\left[\dfrac{1}{2 a},+\infty\right)\)单调递增，
\(\therefore f(x) \geq f\left(\dfrac{1}{2 a}\right)=\dfrac{4 a^{2}-1}{4 a}\)，
若\(\dfrac{4 a^{2}-1}{4 a} \geq-a\)，即\(\dfrac{\sqrt{2}}{4} \leq a<\dfrac{\sqrt{2}}{2}\)时，\(f(x)_{\min }=f(0)=-a\)，
若\(\dfrac{4 a^{2}-1}{4 a}<-a\)，即\(0<a<\dfrac{\sqrt{2}}{4}\)时，\(f(x)_{\min }=f\left(\dfrac{1}{2 a}\right)=\dfrac{4 a^{2}-1}{4 a}\)，
综上\(f(x)_{\min }=\left\{\begin{array}{l} \dfrac{4 a^{2}-1}{4 a}, 0<a<\dfrac{\sqrt{2}}{4} \\ -a, a \geq \dfrac{\sqrt{2}}{4} \end{array}\right.\)．
【点拨】
① 遇到绝对值，可利用\(|x|=\left\{\begin{aligned} -x, & x<0 \\ x, & x \geq 0 \end{aligned}\right.\)去掉绝对值符号，本题函数变成了分段函数；
② 函数最值或值域均与函数的单调性密不可分，了解到函数的单调性相当清晰函数的大致图像，最值便易于求解；而二次函数的单调性与函数的对称轴和开口方向有关；
③ 在分类讨论时，注意结合函数图像进行思考找到分类讨论的“临界值”.
 

巩固练习

1(★★)已知函数\(f(x)=\dfrac{2 x+1}{x-1}\)，其定义域是\([-8 ,-4)\)，则下列说法正确的是(　　)
A．\(f(x)\)有最大值\(\dfrac{5}{3}\)，无最小值
B．\(f(x)\)有最大值\(\dfrac{5}{3}\)，最小值\(\dfrac{7}{5}\)
C．\(f(x)\)有最大值\(\dfrac{7}{5}\)，无最小值
D．\(f(x)\)有最大值\(2\)，最小值\(\dfrac{7}{5}\)
 

2(★★)若\(f(x)=\left\{\begin{array}{l} \dfrac{a}{x}, x \geq 1 \\ -x+3 a, x<1 \end{array}\right.\)是\(R\)上的单调减函数，则实数\(a\)的取值范围为\(\underline{\quad \quad }\)．
 

3(★★)若函数\(f(x)=x^2-2ax+1-a\)在\([0 ,2]\)上的最小值为\(-1\)．则\(a=\)\(\underline{\quad \quad }\)．
 

4(★★)已知函数\(f(x)=\sqrt{x-2}\)，若\(f\left(2 a^{2}-5 a+4\right)<f\left(a^{2}+a+4\right)\)，则实数\(a\)的取值范围是\(\underline{\quad \quad }\)．
 

5(★★)已知函数\(f(x)=|x-1|+|2x+a|\)的最小值为\(2\)，则实数\(a\)的值为\(\underline{\quad \quad }\)．
 

6(★★★)已知函数\(f(x)=2 x-\dfrac{a}{x}\)的定义域为\((0，1]\)(\(a\)为实数)．
(1)当\(a=1\)时，求函数\(y=f(x)\)的值域；
(2)求函数\(y=f(x)\)在区间\((0，1]\)上的最大值及最小值，并求出当函数\(f(x)\)取得最值时\(x\)的值．
 
 

参考答案

1.\(A\)

2.\(\left[\dfrac{1}{2},+\infty\right)\)

3.\(1\)

4.\(\left(0, \dfrac{1}{2}\right] \cup[2,6)\)

5.\(-6\)或\(2\)

6.\((1) (-∞，1]\)

\((2)\)当\(a≥0\)时，无最小值，当\(x=1\)时取得最大值\(2-a\);
当\(a≤-2\)时，无最大值，当\(x=1\)时取得最小值\(2-a\);
当\(-2<a<0\)时，无最大值,当\(x=\sqrt{-\dfrac{a}{2}}\)时取得最小值\(2 \sqrt{-2 a}\).
 

【题型四】 抽象函数的单调性

定义在\((0 ,+∞)\)上的函数\(f(x)\)满足\(f(xy)=f(x)+f(y)\)对所有的正数\(x\)、\(y\)都成立，
\(f(2)=-1\)且当\(x>1\)，\(f(x)<0\)．
(1)求\(f(1)\)的值
(2)判断并证明函数\(f(x)\)在\((0 ,+∞)\)上的单调性
(3)若关于\(x\)的不等式\(f(kx)-f(x^2-kx+1)≥1\)在\((0 ,+∞)\)上恒成立，求实数\(k\)的取值范围.
【解析】(1)\(∵f(xy)=f(x)+f(y)\)，
取\(x=1\)，\(y=1\)得\(f(1)=f(1)+f(1)\)；
\(∴f(1)=0\)；
(2)设\(x_1>x_2>0\)，
则\(f\left(x_{1}\right)-f\left(x_{2}\right)=f\left(x_{2} \cdot \dfrac{x_{1}}{x_{2}}\right)-f\left(x_{2}\right)=f\left(\dfrac{x_{1}}{x_{2}}\right)\)
\({\color{Red}{ (定义法证明) }}\)
\(∵x_1>x_2>0\)；
\(\therefore \dfrac{x_{1}}{x_{2}}>1\)；
又\(x>1\)时，\(f(x)<0\)；\(\therefore f\left(\dfrac{x_{1}}{x_{2}}\right)<0\)；
\(∴f(x_1 )-f(x_2)<0\)，\(∴f(x_1)<f(x_2)\)；
\(∴f(x)\)在\((0 ,+∞)\)上单调递减；
(3)\(∵f(2)=-1\)，\(f(xy)=f(x)+f(y)\)；
由\(f(kx)-f(x^2-kx+1)≥1\)\(⇒f(kx)-1≥f(x^2-kx+1)\)
\(⇒f(kx)+f(2)≥f(x^2-kx+1)\)\(⇒f(2kx)≥f(x^2-kx+1)\)
又\(f(x)\)在\((0 ,+∞)\)上单调递减，
\(\therefore\left\{\begin{array}{l} 2 k x>0 \\ x^{2}-k x+1>0 \\ 2 k x \leq x^{2}-k x+1 \end{array}\right.\)
\(\Rightarrow\left\{\begin{array}{l} k>0 \\ k<x+\dfrac{1}{x} \\ k \leq \dfrac{1}{3}\left(x+\dfrac{1}{x}\right) \end{array}\right.\)
\(\Rightarrow\left\{\begin{array}{l} k>0 \\ k<2 \\ k \leq \dfrac{2}{3} \end{array}\right.\)
\(\Rightarrow 0<k \leq \dfrac{2}{3}\)
【点拨】
① 求具体值时，要大胆尝试，可取特殊值，如\(x=1\)、\(x=0\)等，可取特殊关系，如\(x=y\).
② 抽象函数的单调性用函数的定义法证明，具体的思路有
(1) 作差法 令\(x_1>x_2\)再根据题意“凑出”\(f(x_1 )-f(x_2)\)，证明其大于\(0\)或者小于\(0\);
(2) 作商法 令\(x_1>x_2\)再根据题意“凑出”\(\dfrac{f\left(x_{1}\right)}{f\left(x_{2}\right)}\)，证明其大于\(1\)或者小于\(1\)，此时还要注意\(f(x)>0\)是否成立；
③ 涉及抽象函数，解类似“\(f(kx)-f(x^2-kx+1)≥1\)”这样的不等式，都要利用函数的单调性去掉\(“f”\);
④ 恒成立问题可用分离参数法，最终转化为最值问题，如\(x^2-kx+1>0\)\((x>0)\)恒成立等价于\(k<x+\dfrac{1}{x}(x>0)\)，即求\(f(x)=x+\dfrac{1}{x}\)在\((0 ,+∞)\)上的最小值.
 

巩固练习

1(★★★)定义在\((0 ,+∞)\)上的函数\(f(x)\)满足下面三个条件：
① 对任意正数\(a\),\(b\)，都有\(f(a)+f(b)=f(ab)\)；
② 当\(x>1\)时，\(f(x)<0\)；
③\(f(2)=-1\)
(1)求\(f(1)\)和\(f\left(\dfrac{1}{4}\right)\)的值；
(2)试用单调性定义证明：函数\(f(x)\)在\((0 ,+∞)\)上是减函数；
(3)求满足\(f(4x^3-12x^2)+2>f(18x)\)的\(x\)的取值集合．
 
 
 

答案

1.\((1)\)\(f(1)=0, f\left(\dfrac{1}{4}\right)=2\)
\((2)\)略，提示：定义法
\((3)x∈(3 ,6)\)