3.1 函数的概念及其表示方法
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册函数同步拔高,难度3颗星!
模块导图
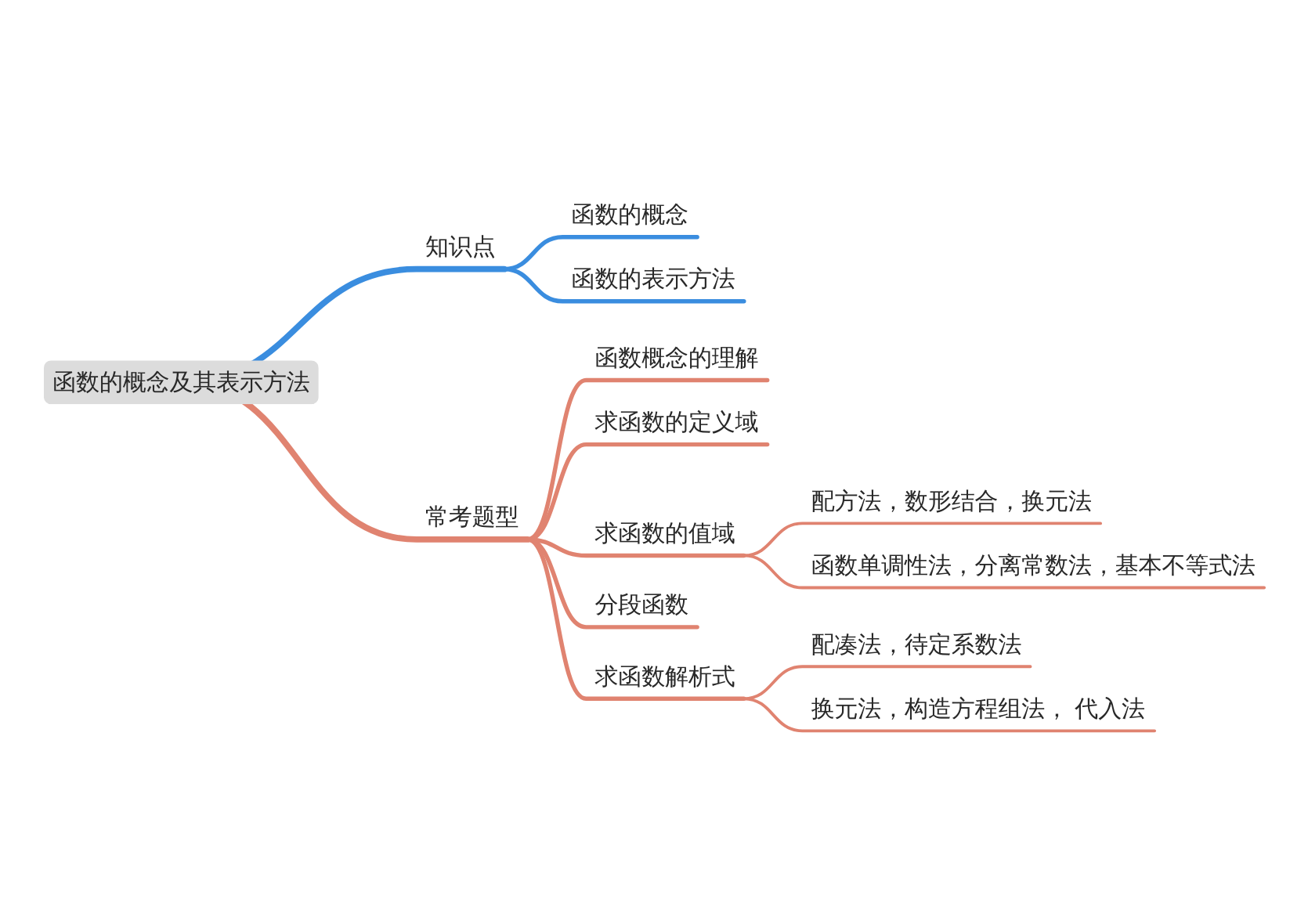
知识剖析
函数的概念
1 概念
设\(A\)、\(B\)是非空的数集,如果按照某个确定的对应关系\(f\),使对于集合\(A\)中的任意一个数\(x\),在集合\(B\)中都有唯一确定的数\(f(x)\)和它对应,那么就称\(f:A→B\)为从集合\(A\)到集合\(B\)的一个函数.记作:\(y=f(x) ,x∈A\).其中,\(x\)叫做自变量,\(x\)的取值范围\(A\)叫做函数的定义域;与\(x\)的值相对应的\(y\)值叫做函数值,函数值的集合\(\{f(x) \mid x \in A\}\)叫做函数的值域.
2 定义域
① 概念 函数自变量\(x\)的取值范围.
② 求函数的定义域主要应考虑以下几点
\((1)\)分式的分母不等于零;
\((2)\)偶次方根的被开方数不小于零;
\((3)\)对数式的真数必须大于零;
\((4)\)指数、对数式的底必须大于零且不等于1;
\((5)\)指数为零底不可以等于零;
\((6)\)抽象函数的定义域较为复杂.
3 值域
① 概念 函数值\(y\)的取值范围
② 求值域的方法
\((1)\)配方法
\((2)\)数形结合
\((3)\)换元法
\((4)\)函数单调性法
\((5)\)分离常数法
\((6)\)基本不等式法
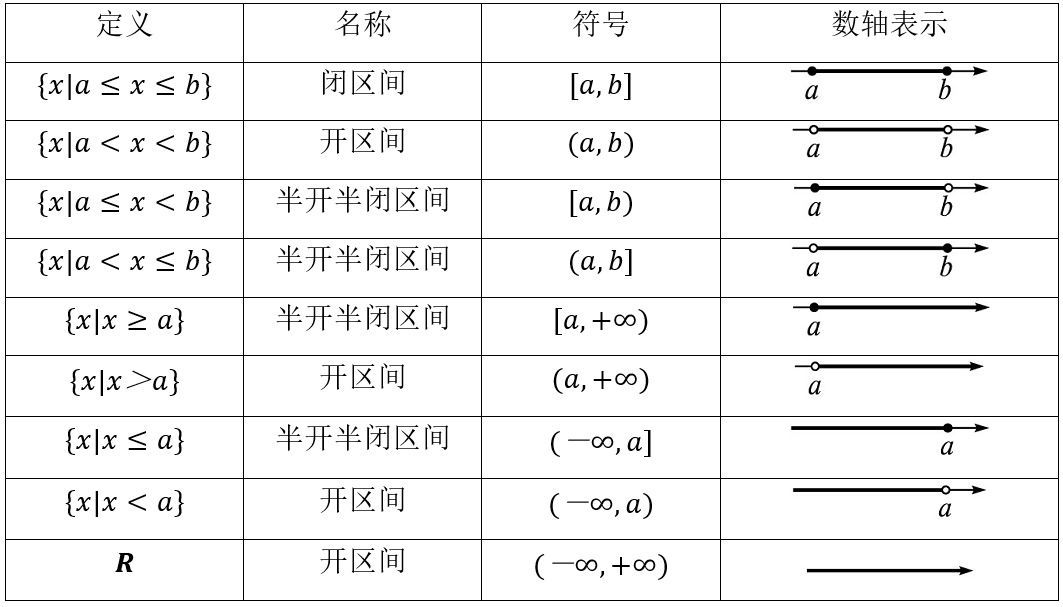
4 区间
函数的表示方法
1 表格法
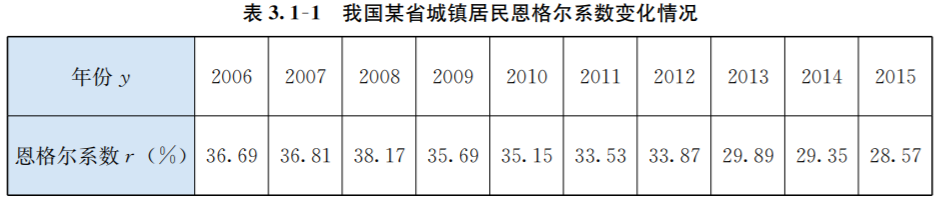
如上表,我们很容易看到\(y\)与\(r\)之间的函数关系.
在初中刚学画一次函数图像时,第一步就是列表,其实就是用表格法表示一次函数.
2 图像法
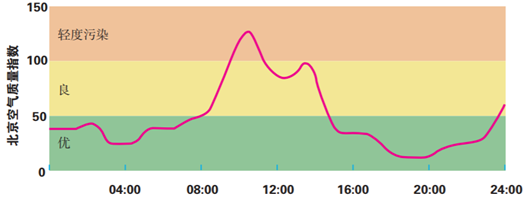
如上图,很清晰的看到某天空气质量指数\(I\)与时间\(t\)两个变量之间的关系,特别是其趋势.
数学中的“数形结合”也就是这回事,它是数学一大思想,在高中解题中识图和画图尤为重要.
3 解析式
求函数解析式的方法
\((1)\)配凑法
\((2)\)待定系数法
\((3)\)换元法
\((4)\)构造方程组法
\((5)\)代入法
经典例题
【题型一】 函数概念的理解
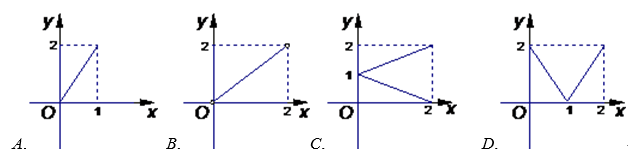
【典题1】设集合\(M=\{x \mid 0 \leq x \leq 2\}\),\(N=\{y \mid 0 \leq y \leq 2\}\), 给出如下四个图形,其中能表示从集合\(M\)到集合\(N\)的函数关系的是( )
【解析】
\({\color{Red}{(本题相当把M=\{x \mid 0 \leq x \leq 2\}看成定义域, N=\{y \mid 0 \leq y \leq 2\}看成值域) }}\)
图象\(A\)不满足条件,因为当\(1<x≤2\)时,\(N\)中没有\(y\)值与之对应.
图象\(B\)不满足条件,因为当\(x=2\)时,\(N\)中没有\(y\)值与之对应.
图象\(C\)不满足条件,因为对于集合\(M=\{x \mid 0 \leq x \leq 2\}\)中的每一个\(x\)值,在集合\(N\)中有\(2\)个\(y\)值与之对应,不满足函数的定义.
只有\(D\)中的图象满足对于集合\(M=\{x \mid 0 \leq x \leq 2\}\)中的每一个\(x\)值,在\(N=\{y \mid 0 \leq y \leq 2\}\)中都有唯一确定的一个\(y\)值与之对应,故选\(D\).
【典题2】给定的下列四个式子中,能确定\(y\)是\(x\)的函数的是( )
①\(x^2+y^2=1\)
②\(|x-1|+\sqrt{y^{2}-1}=0\)
③\(\sqrt{x-1}+\sqrt{y-1}=1\)
④\(y=\sqrt{x-2}+\sqrt{1-x}\)
A.① \(\qquad \qquad \qquad \qquad\) B.② \(\qquad \qquad \qquad \qquad\) C.③ \(\qquad \qquad \qquad \qquad\) D.④
【解析】①由\(x^2+y^2=1\)得\(y=\pm \sqrt{1-x^{2}}\),不满足函数的定义,
比如\(x=0\),\(y=±1\),所以①不是函数.
②由\(|x-1|+\sqrt{y^{2}-1}=0\)
得\(|x-1|=0\),\(\sqrt{y^{2}-1}=0\),
所以\(x=1\),\(y=±1\),所以②不是函数.
③由\(\sqrt{x-1}+\sqrt{y-1}=1\)得\(y=(1-\sqrt{x-1})^{2}+1\),满足函数的定义,所以③是函数.
④要使函数\(y=\sqrt{x-2}+\sqrt{1-x}\)有意义,
则\(\left\{\begin{array}{l}
x-2 \geq 0 \\
1-x \geq 0
\end{array}\right.\),解得\(\left\{\begin{array}{l}
x \geq 2 \\
x \leq 1
\end{array}\right.\),此时不等式组无解,所以④不是函数.
故选:\(C\).
【点拨】函数中自变量\(x\)与函数值\(y\)的关系是“一对一或多对一”的关系,不能是“一对多”.
【题型二】求函数的定义域
【典题1】函数\(y=\dfrac{\sqrt{-x^{2}+2 x+3}}{x}\)的定义域是\(\underline{\quad \quad }\).
【解析】要使函数有意义,
则\(\left\{\begin{array}{c}
-x^{2}+2 x+3 \geq 0 \\
x \neq 0
\end{array}\right.\),即\(\left\{\begin{array}{c}
-1 \leq x \leq 3 \\
x \neq 0
\end{array}\right.\).
即\(-1≤x<0\)或\(0<x≤3\),
即函数的定义域为\([-1 ,0)⋃(0 ,3]\).
【典题2】下列各组函数中表示的函数不同的是 ( )
A.\(f(x)=x\),\(g(x)=\sqrt[3]{x^{3}}\)
B.\(f(x)=\sqrt{x^{2}}\),\(g(x)=|x|\)
C.\(f(x)=x^2-3x\),\(g(t)=t^2-3t\)
D.\(f(x)=\dfrac{x^{2}-4}{x-2}\),\(g(x)=x+2\)
【解析】\(A\),\(B\),\(C\)的定义域和对应法则相同,表示同一函数,
\(D\)中\(g(x)=x+2\)的定义域是\(R\),\(f(x)=\dfrac{x^{2}-4}{x-2}\)定义域为\(\{x|x≠2\}\),两个函数的定义域不相同,不是同一函数.
故选:\(D\).
【点拨】
① 判断两个函数是否是同一函数,看函数的定义域和解析式是否均相同;
② 函数反应的是两个变量的关系,至于用什么字母表示都一样,故选项\(C\)的\(f(x)=x^2-3x\),\(g(t)=t^2-3t\)是同一函数.
【典题3】已知\(f(x^2-1)\)定义域为\([0 ,3]\),求\(f(2x-1)\)的定义域.
【解析】\(∵0≤x≤3\)
\(∴-1≤x^2-1≤8\)
\(∴-1≤2x-1≤8\)
\(\therefore 0 \leq x \leq \dfrac{9}{2}\)
故函数\(f(2x-1)\)的定义域是\(\left[0, \dfrac{9}{2}\right]\).
【点拨】抽象函数的定义域理解起来不容易,由于函数的解析式与字母的选择无关,若把题目换成“已知\(f(x^2-1)\)定义域为\([0 ,3]\),求\(f(2t-1)\)的定义域.”好理解多了,
① 谨记定义域指的是自变量的取值范围,所以由“\(f(x^2-1)\)定义域为\([0 ,3]\)”得到的是“\(0≤x≤3\)”,“求\(f(2t-1)\)的定义域”指的就是求\(t\)的范围.
② 把“\(x^2-1\)”和“\(2t-1\)”都看成整体,它们的范围是相等的,这样就有“\(-1≤x^2-1≤8\)\(⇒-1≤2t-1≤8\)”.
【题型三】求函数的值域
方法1 配方法
【典题1】求函数\(y=\dfrac{5 x^{2}-4 x+1}{x^{2}}\)在区间\(x \in\left[\dfrac{1}{4}, 1\right]\)的值域.
【解析】\(y=\dfrac{5 x^{2}-4 x+1}{x^{2}}\)\(=\dfrac{1}{x^{2}}-\dfrac{4}{x}+5=\left(\dfrac{1}{x}-2\right)^{2}+1\)
\(\because x \in\left[\dfrac{1}{4}, 1\right]\)
\(\therefore \dfrac{1}{x} \in[1,4]\),\(\therefore 1 \leq\left(\dfrac{1}{x}-2\right)^{2}+1 \leq 5,\)
即\(y=\dfrac{5 x^{2}-4 x+1}{x^{2}}\)在区间\(x \in\left[\dfrac{1}{4}, 1\right]\)的值域\([1 ,5]\).
【点拨】配方法针对二次函数型的函数值域.
方法2 数形结合
【典题2】求函数\(f(x)=\left\{\begin{array}{c}
2 x-x^{2},(0 \leq x \leq 3) \\
x^{2}+6 x,(-2 \leq x \leq 0)
\end{array}\right.\)的值域.
【解析】\({\color{Red}{(这是分段函数,两段函数均为二次函数,其图像易得,故可用数形结合求值域)}}\)
\(f(x)=2 x-x^2=-(x-1)^2+1\),开口向下,最大值为\(f(1)=1\),
而\(f(0)=0\),\(f(3)=-3\),
\(f(x)=x^2+6 x=(x+3)^2-9\), 开口向上,而\(f(-2)=-8\),\(f(0)=0\),
可得到函数图像如图,
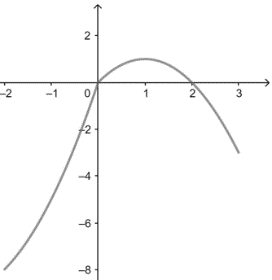
易得函数值域为\([-8 ,1]\).
【点拨】数形结合最大的好处是直观.
方法3 换元法
【典题3】求函数\(f(x)=2 x+\sqrt{1-x}\)的值域.
【解析】令\(t=\sqrt{1-x} \quad(t \geq 0)\),
\({\color{Red}{(要注意新变量t的取值范围)}}\)
得\(x=-t^2+1\),
\(∴\)原函数化为\(y=-2 t^{2}+t+2\)\(=-2\left(t-\dfrac{1}{4}\right)^{2}+\dfrac{17}{8} \leq \dfrac{17}{8}\)
\({\color{Red}{ (把函数转化为二次函数值域问题)}}\)
\(∴\)函数\(y=f(x)\)的值域为\(\left(-\infty, \dfrac{17}{8}\right]\).
【点拨】本题利用换元法把不熟悉函数值域问题转化为熟悉的二次函数值域问题,即求函数\(f(x)=2 x+\sqrt{1-x}\)的值域\(⇔y=-2t^2+t+2 (t≥0)\)的值域,其中特别注意\(t≥0\)不能忽略!这正是体现了数学中的“等价转化”思想.
【典题4】函数\(f(x)=-9^{-x}+\left(\dfrac{1}{3}\right)^{x-1}+\dfrac{3}{4}\)在\([-1 ,+∞)\)上的值域为\(\underline{\quad \quad }\).
【解析】\(f(x)=-9^{-x}+\left(\dfrac{1}{3}\right)^{x-1}+\dfrac{3}{4}\)\(=-\left(\dfrac{1}{3}\right)^{2 x}+3 \times\left(\dfrac{1}{3}\right)^{x}+\dfrac{3}{4}\),
\({\color{Red}{(本题主要是注意到了9^{-x}和\left(\dfrac{1}{3}\right)^{x-1}均可\left(\dfrac{1}{3}\right)^{x}或3^x的形式,故想到换元法) }}\)
令\(t=\left(\dfrac{1}{3}\right)^{x}\),
因为\(x∈[-1 ,+∞)\),所以\(t∈(0 ,3]\),
原函数的值域等价于函数\(g(t)=-t^{2}+3 t+\dfrac{3}{4}=-\left(t-\dfrac{3}{2}\right)^{2}+3\)\((0<t \leq 3)\)的值域,
由二次函数的性质可知\(f(x)=\left[\dfrac{3}{4}, 3\right]\),
即所求函数的值域为\(\left[\dfrac{3}{4}, 3\right]\).
【点拨】
① 换元法的本质就是“整体思想”,它能把“不太友善的”表示形式转化为“友善的”,前2题均用换元法把复杂形式函数转化为二次函数,故解题过程中特别要注意式子的结构特征.
② 换元法要注意换元后变量的取值范围,比如典题3的“\(t≥0\)”, 典题4中的“\(t∈(0 ,3]\)".
方法4 函数单调性法
【典题5】函数\(f(x)=2^{x^{2}-2 x+3}\),\(x∈[0 ,3]\)的值域为\(\underline{\quad \quad }\).
【解析】由复合函数的单调性可知,
函数\(f(x)\)在\([0 ,1]\)上单减,在\([1 ,3]\)上单增,
又\(f(0)=2^3=8\),\(f(1)=2^2=4\),\(f(3)=2^6=64\),
\(∴\)函数值域为\([4 ,64]\).
【点拨】
① 利用函数单调性是求函数值域最常见的方法,高二还会学到导数,它是一把利器.
② 复合函数的单调性是"同增异减".
方法5 分离常数法
【典题6】求函数\(f(x)=\dfrac{2 x^{2}-1}{x^{2}+1}\)的值域.
【解析】函数\(f(x)=\dfrac{2 x^{2}-1}{x^{2}+1}=\dfrac{2\left(x^{2}+1\right)-3}{x^{2}+1}\)\(=\dfrac{2\left(x^{2}+1\right)}{x^{2}+1}-\dfrac{3}{x^{2}+1}=2-\dfrac{3}{x^{2}+1}\),
\({\color{Red}{ (在分子2x^2-1中“凑出”分母x^2+1,最终达到“分式中的分子是个常数3”的目的)}}\)
\(∵x^2+1≥1\),
\(\therefore 0<\dfrac{1}{x^{2}+1} \leq 1\)\(\Rightarrow-3 \leq-\dfrac{3}{x^{2}+1}<0\)\(\Rightarrow-1 \leq 2-\dfrac{3}{x^{2}+1}<2\),
故函数\(f(x)=\dfrac{x^{2}-1}{x^{2}+1}\)的值域是\([-1 ,2)\).
【点拨】形如\(f(x)=\dfrac{a \cdot g(x)+b}{c \cdot g(x)+d}\)均可用分离常数法求函数值域,比如求函数\(y=\dfrac{3 x+1}{4 x-2}\),\(y=\dfrac{3 \cdot 2^{x}+4}{2^{x}-1}\)的值域.
方法6 基本不等式法(对勾函数法)
【典题7】求函数\(f(x)=\dfrac{x^{2}+4 x+1}{x^{2}+1}(x \geq 0)\)的值域.
【解析】\(\because f(x)=\dfrac{x^{2}+4 x+1}{x^{2}+1}\)\(=\dfrac{x^{2}+1}{x^{2}+1}+\dfrac{4 x}{x^{2}+1}=1+\dfrac{4 x}{x^{2}+1}\),
\({\color{Red}{(也有点分离常数法的感觉) }}\)
\(∴\)①当\(x=0\)时,\(f(x)=1\);\({\color{Red}{(x=0这个不能漏)}}\)
②当\(x>0\)时,
\(0<\dfrac{4 x}{x^{2}+1}=\dfrac{4}{x+\dfrac{1}{x}}\)\(\leq \dfrac{4}{2 \sqrt{x \cdot \dfrac{1}{x}}}=2\),
当且仅当\(x=1\)时“=”成立,此时\(1<f(x)≤3\)
\({\color{Red}{ (利用对勾函数y=x+\dfrac{1}{x}(x>0)的图像求解也可以)}}\)
\(∴\)函数\(y=f(x)\)的值域为\([1,3]\).
【点拨】利用基本不等式法(对勾函数法)能处理二次分式函数\(y=\dfrac{d x^{2}+e x+f}{a x^{2}+b x+c}\)的值域.
巩固练习
1(★)函数\(y=f(x-1)\)与函数\(y=f(x+1)\)( )
A.是同一个函数 \(\qquad \qquad\)B.定义域相同 \(\qquad \qquad\)C.图象重合 \(\qquad \qquad\)D.值域相同
2(★)函数\(f(x)=\sqrt{-x^{2}+4 x+12}+\dfrac{1}{x-4}\)的定义域为\(\underline{\quad \quad }\) .
3(★★)已知函数\(f(x+1)\)定义域为\([1 ,4]\),则函数\(f(x-1)\)的定义域为\(\underline{\quad \quad }\).
4(★★)函数\(y=2-\sqrt{-x^{2}+4 x}\)的值域是为\(\underline{\quad \quad }\).
5(★★)函数\(y=\sqrt{x-1}+\sqrt{x+1 }\)\((x \geq 1)\)的值域为\(\underline{\quad \quad }\).
6(★★)函数\(f(x)=\dfrac{x-1}{x+3}(x \geq 1)\)的值域为\(\underline{\quad \quad }\).
7(★★)函数\(y=4^{x}+2^{x+1}+3\)的值域为\(\underline{\quad \quad }\).
8(★★★)求函数\(y=\dfrac{2 x^{2}-x+1}{2 x-1}\)\(\left(x>\dfrac{1}{2}\right)\)的值域.
参考答案
1.\(D\)
2.\([-2,4)∪(4,6]\)
3.\([3 ,6]\)
4.\([0,2]\)
5.\([\sqrt{2},+\infty]\)
6.\([0,1)\)
7.\((3 ,+∞)\)
8.\(\left[\dfrac{1}{2}+\sqrt{2},+\infty\right)\)
【题型四】分段函数
【典题1】设函数\(f(x)= \begin{cases}x^{2}+2 & (x \leq 2) \\ 2 x & (x>2)\end{cases}\),若\(f(x_0)=8\),则\(x_0=\)\(\underline{\quad \quad }\).
【解析】由题意,得
①当\(x_0≤2\)时,有\(x_0^2+2=8\),解之得\(x_{0}=\pm \sqrt{6}\),
而\(\sqrt{6}>2\)不符合,所以\(x_{0}=-\sqrt{6}\);
②当\(x_0>2\)时,有\(2x_0=8\),解之得\(x_0=4\).
综上所述,得\(x_0=4\)或\(-\sqrt{6}\).
【典题2】 已知函数\(f(x)=\left\{\begin{array}{l}
x^{2}-6 x+6, x \geq 0 \\
3 x+4, x<0
\end{array}\right.\),若互不相等的实数\(x_1\),\(x_2\),\(x_3\)满足\(f(x_1)=f(x_2)=f(x_3)\),则\(x_1+x_2+x_3\)的取值范围为\(\underline{\quad \quad }\) .
【解析】 \({\color{Red}{ 乍眼一看,不太理解题意,设f(x_1 )=t,本题就函数y=t与y=f(x)交点横坐标的问题,自然想到数形结合)}}\)
函数\(f(x)=\left\{\begin{array}{l}
x^{2}-6 x+6, x \geq 0 \\
3 x+4, x<0
\end{array}\right.\)的图象如图,
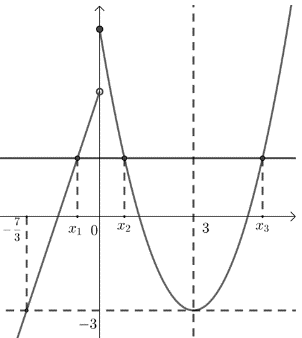
不妨设\(x_1<x_2<x_3\),
则\(x_2\),\(x_3\)关于直线\(x=3\)对称,故\(x_2+x_3=6\),
且\(x_1\)满足\(-\dfrac{7}{3}<x_{1}<0\);
则\(x_1+x_2+x_3\)的取值范围是\(-\dfrac{7}{3}+6<x_{1}+x_{2}+x_{3}<0+6\);
即\(x_{1}+x_{2}+x_{3} \in\left(\dfrac{11}{3}, 6\right)\).
【点拨】分段函数本质上是“分类讨论”,特别要注意“每段函数”的定义域.处理分段函数的性质问题(值域、交点等)常常用数形结合的方法.
【题型五】求函数解析式
方法1 配凑法
【典题1】已知\(f\left(x+\dfrac{1}{x}\right)=x^{2}+\dfrac{1}{x^{2}}(x>0)\), 求\(f(x)\)的解析式.
【解析】\(∵x>0\)\(\therefore x+\dfrac{1}{x} \geq 2\)
\(\because f\left(x+\dfrac{1}{x}\right)=\left(x+\dfrac{1}{x}\right)^{2}-2\),
\(∴ f(x)=x^2-2 (x≥2)\)(注意函数的定义域)
【点拨】本题主要是观察到\(x+\dfrac{1}{x}\)与\(x^{2}+\dfrac{1}{x^{2}}\)之间存在“完成平方”的关系.
方法2 待定系数法
【典题2】已知函数\(f(x)\)是二次函数,若\(f(0)=0\),且\(f(x+1)=f(x)+x+1\),求\(f(x)\)的解析式.
【解析】依题意可设\(f(x)=ax^2+bx+c(a≠0)\),
若\(f(0)=0\),且\(f(x+1)=f(x)+x+1\),
\(∴c=0\)且\(a(x+1)^2+b(x+1)+c=ax^2+bx+c+x+1\)
即\(c=0\)且\((2a+b)x+a+b+c=(b+1)x+c+1\),
\(\therefore\left\{\begin{array}{c}
c=0 \\
2 a+b=b+1 \\
a+b+c=c+1
\end{array}\right.\),
解得\(a=\dfrac{1}{2}\),\(b=\dfrac{1}{2}\),\(c=0\).
\(\therefore f(x)=\dfrac{x^{2}+x}{2}\)
【点拨】当函数的类型已知,利用待定系数法可求函数解析式.
方法3 换元法
【典题3】已知\(f(\sqrt{x}+1)=x+2 \sqrt{x}\), 求\(f(x+1)\).
【解析】令\(t=\sqrt{x}+1\),则\(t≥1\),\(x=(t-1)^2\),
\(\because f(\sqrt{x}+1)=x+2 \sqrt{x}\)
\(∴ f(t)=(t-1)^2+2(t-1)=t^2-1\)
\(∴ f(x)=x^2-1 (x≥1)\)
\(∴ f(x+1)=(x+1)^2-1=x^2+2x (x≥0)\).
【点拨】
① 用换元法时注意新变量的取值范围.
② 用配凑法\(f(\sqrt{x}+1)=x+2 \sqrt{x}\)\(=(\sqrt{x}+1)^{2}-1\)\(\Rightarrow f(x)=x^{2}-1(x \geq 1)\),但要求观察力足够好.
方法4 构造方程组法
【典题4】设\(f(x)\)满足\(f(x)-2 f\left(\dfrac{1}{x}\right)=x\), 求\(f(x)\)的解析式.
【解析】 \(\because f(x)-2 f\left(\dfrac{1}{x}\right)=x\)①
显然\(x≠ 0\),将\(x\)换成\(\dfrac{1}{x}\),
得\(f\left(\dfrac{1}{x}\right)-2 f(x)=\dfrac{1}{x}\)②
解①②联立的方程组,得\(f(x)=-\dfrac{x}{3}-\dfrac{2}{3 x}\).
方法5 代入法
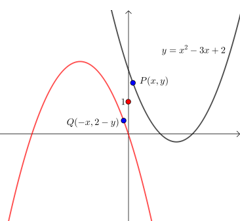
【典题5】与函数\(y=x^2-3x+2\)的图象关于点\((0,1)\)对称的函数是\(\underline{\quad \quad }\).
【解析】 设\(P(x ,y)\)为所求函数图象上的任意一点,
它关于点\((0,1)\)对称的点是\(Q(-x ,2-y)\).
由题意知点\(Q(-x ,2-y)\)在函数\(y=x^2-3x+2\)的图象上,
则\(2-y=x^2+3x+2\),
化简得\(y=-x^2-3x\).
【点拨】
① 由下图可对本题有个更清晰的理解.
② 求与一已知函数关于点对称或轴对称的函数解析式均可以用“代入法”.若把本题的函数\(y=x^2-3x+2\)换成\(y=2^x\)或者把“关于点\((0,1)\)对称”换成“关于\(y=-1\)对称”,其解题过程大同小异.
巩固练习
1(★)已知函数\(y=\left\{\begin{array}{l} x^{2}+1(x \leq 0) \\ 2 x(x>0) \end{array}\right.\),若\(f(a)=10\),则\(a\)的值是\(\underline{\quad \quad }\).
2(★★)已知函数\(f(x)=\left\{\begin{array}{l}
(2 a-1) x+7 a-2(x<1) \\
a^{x}(x \geq 1)
\end{array}\right.\)在\((-∞ ,+∞)\)上单调递减,则实数\(a\)的取值范围为\(\underline{\quad \quad }\).
3(★★)已知一次函数\(f(x)\)满足条件\(f(x+1)+f(x)=2x\),求函数\(f(x)\)的解析式.
4(★★)已知\(f(\sqrt{x})=x^{2}-2 x\),求函数\(f(x)\)的解析式.
5(★★★)已知\(f(0)=1\),对于任意实数\(x\),\(y\),等式\(f(x-y)=f(x)-y(2x-y+1)\),求\(f(x)\)的解析式.
参考答案
1.\(-3\)或\(5\)
2.\(\left[\dfrac{3}{8}, \dfrac{1}{2}\right)\)
3.\(f(x)=x-\dfrac{1}{2}\)
4.\(f(x)=x^4-2x^2 (x≥0)\)
5.\(f(x)=x^2+x+1\)

