6.4 平面向量的应用
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高一数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
必修第二册同步拔高,难度3颗星!
模块导图
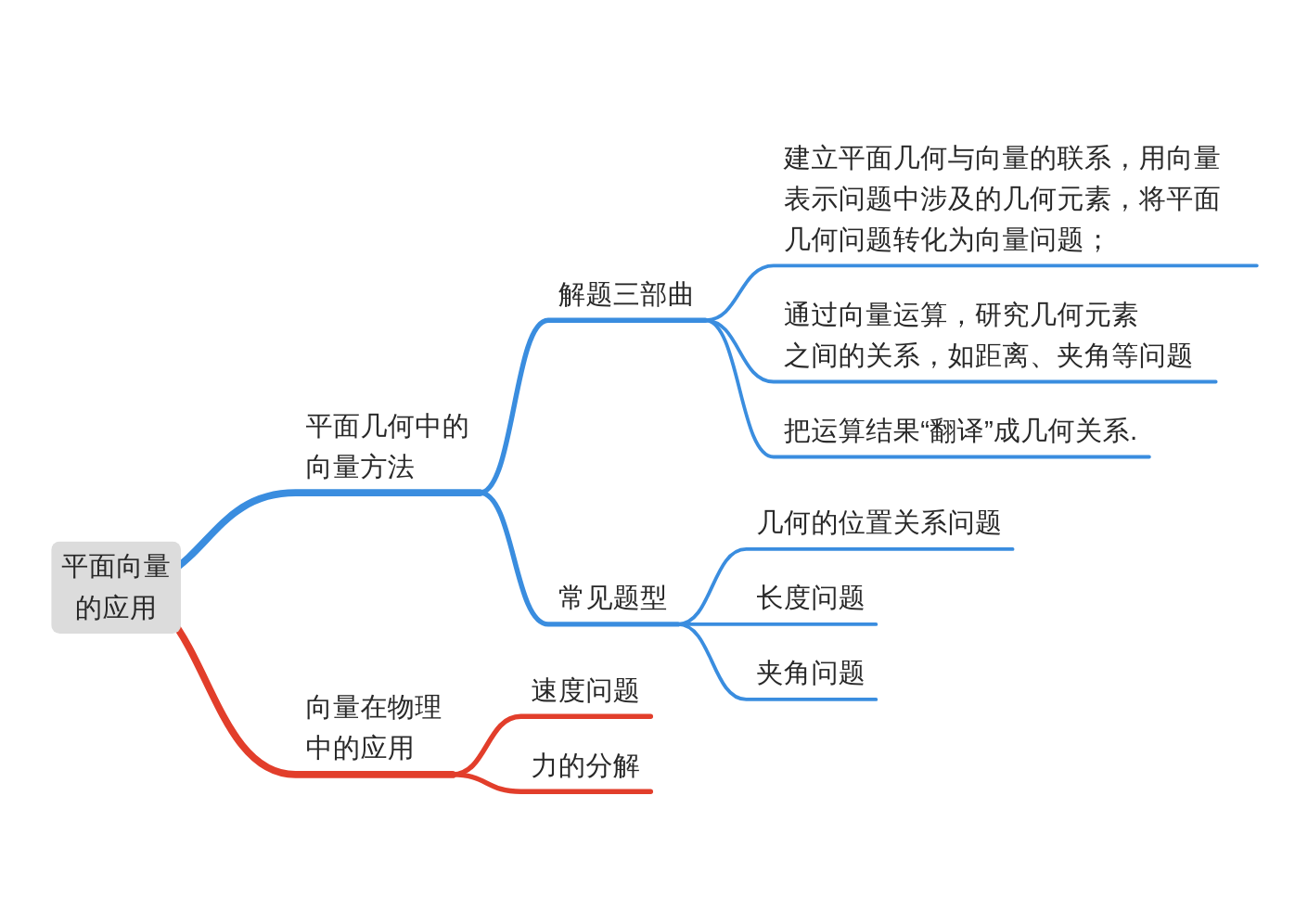
知识剖析
平面几何中的向量方法
1 由于向量的线性运算和数量积运算具有鲜明的几何背景,平面几何图形的许多性质,如全等、相似、长度、夹角等都可以由向量的线性运算及数量积表示出来,因此平面几何中的许多问题都可用向量运算的方法加以解决.
2 用向量方法解决平面几何问题的“三部曲”
(1) 建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2) 通过向量运算,研究几何元素之间的关系,如距离、夹角等问题;
(3) 把运算结果“翻译”成几何关系.
\({\color{Red}{ Eg }}\)点\(A\)、\(B\)、\(C\)、\(D\)不在同一直线上,
\((1)\)证明直线平行或共线:\(A B || C D\Leftrightarrow \overrightarrow{A B}||\overrightarrow{C D}\),
\((2)\)证明直线垂直:\(\overrightarrow{A B} \cdot \overrightarrow{C D}=0 \Leftrightarrow A B \perp C D\)
\((3)\)求线段比值:\(|\lambda| = \dfrac{A B}{C D}且A B||C D\Leftrightarrow\overrightarrow{A B}=\lambda \overrightarrow{C D}\),
\((4)\)证明线段相等:\(\overrightarrow{A B}^{2}=\overrightarrow{C D}^{2} \Leftrightarrow A B=C D\)
向量在物理中的应用
1 速度、力是向量,都可以转化为向量问题;
2 力的合成与分解符合平行四边形法则.
经典例题
【题型一】平面向量在几何中的应用
【典题1】 证明 对角线互相平分的四边形是平行四边形.

【证明】 设四边形\(ABCD\)的对角线\(AC\)、\(BD\)交于点\(O\),且\(AO=OC\),\(BO=OD\)
\(\because \overrightarrow{A B}=\dfrac{1}{2} \overrightarrow{A C}+\dfrac{1}{2} \overrightarrow{D B}, \overrightarrow{D C}=\dfrac{1}{2} \overrightarrow{D B}+\dfrac{1}{2} \overrightarrow{A C}\)
\(\therefore \overrightarrow{A B}=\overrightarrow{D C}\)
即\(AB=DC\)且\(AB//DC\)
所以四边形\(ABCD\)是平行四边形
即对角线互相平分的四边形是平行四边形.
【点拨】
① 证明四边形是平行四边形\(⇔AB=DC\)且\(AB//DC\)\(⇔\overrightarrow{A B}=\overrightarrow{D C}\).
② 证明几何中的平行和长度关系可以转化为向量的倍数关系.
【典题2】 已知平行四边形\(ABCD\)的对角线为\(AC、BD\),求证\(AC^2+BD^2=2(AB^2+AD^2)\)(即对角线的平方和等于邻边平方和的倍).

【证明】 由\(|\overrightarrow{A C}|^{2}=\overrightarrow{A C}^{2}=(\overrightarrow{A B}+\overrightarrow{A D})^{2}\)\(=|\overrightarrow{A B}|^{2}+|\overrightarrow{A D}|^{2}+2 \overrightarrow{A B} \cdot \overrightarrow{A D}\)①
\(|\overrightarrow{D B}|^{2}=\overrightarrow{D B}^{2}=(\overrightarrow{A B}-\overrightarrow{A D})^{2}\)\(=|\overrightarrow{A B}|^{2}+|\overrightarrow{A D}|^{2}-2 \overrightarrow{A B} \cdot \overrightarrow{A D}\)②
两式相加得\(|\overrightarrow{A C}|^{2}+|\overrightarrow{D B}|^{2}=2\left(|\overrightarrow{A B}|^{2}+|\overrightarrow{A D}|^{2}\right)\)
即\(A C^{2}+B D^{2}=2\left(A B^{2}+A D^{2}\right)\)
【点拨】 利用\(|\overrightarrow{A B}|^{2}=|A B|^{2}\)可证明线段长度关系.
【典题3】 用向量方法证明 三角形三条高线交于一点.

【证明】
\({\color{Red}{(分析 设H是高线BE、CF的交点,再证明AH⊥BC,则三条高线就交于一点.)}}\)
设\(H\)是高线\(BE\)、\(CF\)的交点 ,
则有\(\overrightarrow{B H}=\overrightarrow{A H}-\overrightarrow{A B}\),\(\overrightarrow{C H}=\overrightarrow{A H}-\overrightarrow{A C}\),\(\overrightarrow{B C}=\overrightarrow{A C}-\overrightarrow{A B}\)
\(\because \overrightarrow{B H} \perp \overrightarrow{A C}\),\(\overrightarrow{C H} \perp \overrightarrow{A B}\)
\(\therefore(\overrightarrow{A H}-\overrightarrow{A B}) \cdot \overrightarrow{A C}=(\overrightarrow{A H}-\overrightarrow{A C}) \cdot \overrightarrow{A B}=0\)
化简得\(\overrightarrow{A H} \cdot(\overrightarrow{A C}-\overrightarrow{A B})=0\)
\(\therefore \overrightarrow{A H} \cdot \overrightarrow{B C}=0\)则\(AH⊥BC\)
\({\color{Red}{(向量中证明AB⊥CD,只需要证明\overrightarrow{A B} \cdot \overrightarrow{C D}=0)}}\)
所以三角形三条高线交于一点.
【点拨】 本题的思路是:设\(H\)是高线\(BE\)、\(CF\)的交点,再证明\(AH⊥BC\),则三条高线就交于一点.
【典题4】 证明三角形三条中线交于一点.
【证明】 \({\color{Red}{(分析 设BE、AF交于O,证明C、O、D三点共线便可)}}\)
\(AF\)、\(CD\)、\(BE\)是三角形的三条中线
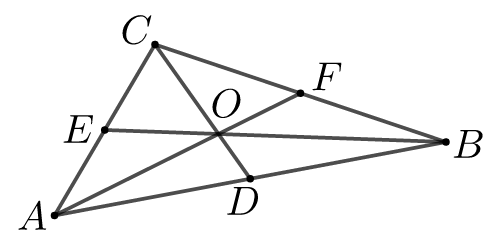
设\(BE\)、\(AF\)交于点\(O\),
\(∵\)点\(D\)是中点,\(\therefore \overrightarrow{C D}=\dfrac{1}{2}(\overrightarrow{C A}+\overrightarrow{C B})\)
连接\(EF\),
易证明\(\Delta A O B \sim \Delta F O E\),且相似比是\(2: 1\),
\(\therefore B O=\dfrac{2}{3} B E\),
\(\therefore \overrightarrow{C O}=\overrightarrow{C B}+\overrightarrow{B O}=\overrightarrow{C B}+\dfrac{2}{3} \overrightarrow{B E}\)\(=\overrightarrow{C B}+\dfrac{2}{3}(\overrightarrow{B A}+\overrightarrow{A E})\)
\(=\overrightarrow{C B}+\dfrac{2}{3}\left(\overrightarrow{B C}+\overrightarrow{C A}+\dfrac{1}{2} \overrightarrow{A C}\right)\)\(=\dfrac{1}{3}(\overrightarrow{C A}+\overrightarrow{C B})\)
\(\therefore \overrightarrow{C O}=\dfrac{2}{3} \overrightarrow{C D}\), 即\(C、O、D\)三点共线,
\({\color{Red}{(向量中证明A、B、C三点共线,只需证明\overrightarrow{A B}=\lambda \overrightarrow{A C})}}\)
\(∴AF、CD、BE\)交于一点,
即三角形三条中线交于一点.
【题型二】平面向量在物理中的应用
【典题1】 如图,已知河水自西向东流速为\(\left|v_{0}\right|=1 \mathrm{~m} / \mathrm{s}\),设某人在静水中游泳的速度为\(v_1\),在流水中实际速度为\(v_2\).
(1)若此人朝正南方向游去,且\(\left|v_{1}\right|=\sqrt{3} \mathrm{~m} / \mathrm{s}\),求他实际前进方向与水流方向的夹角\(α\)和\(v_2\)的大小;
(2)若此人实际前进方向与水流垂直,且\(\left|v_{2}\right|=\sqrt{3} \mathrm{~m} / \mathrm{s}\),求他游泳的方向与水流方向的夹角\(β\)和\(v_1\)的大小.

【解析】 如图,设\(\overrightarrow{O A}=\overrightarrow{v_{0}}\),\(\overrightarrow{O B}=\overrightarrow{v_{1}}\),\(\overrightarrow{O C}=\overrightarrow{v_{2}}\)
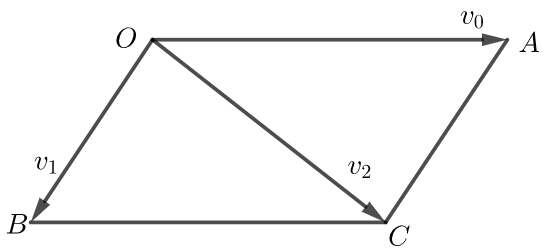
则由题意知\(\overrightarrow{v_{2}}=\overrightarrow{v_{0}}+\overrightarrow{v_{1}}\),\(|\overrightarrow{O A}|=1\)
根据向量加法的平行四边形法则得四边形OACB为平行四边形.
(1)由此人朝正南方向游去得四边形\(OACB\)为矩形,且\(|\overrightarrow{O B}|=A C=\sqrt{3}\),如下图所示,

则在直角\(△OAC\)中,\(\left|\overrightarrow{v_{2}}\right|=O C=\sqrt{O A^{2}+A C^{2}}=2\),
\(\tan \angle A O C=\dfrac{\sqrt{3}}{1}=\sqrt{3}\),
又\(\alpha=\angle A O C \in\left(0, \dfrac{\pi}{2}\right)\),所以\(\alpha=\dfrac{\pi}{3}\);
(2)由题意知\(\alpha=\angle O C B=\dfrac{\pi}{2}\),且\(\left|\overrightarrow{v_{2}}\right|=|O C|=\sqrt{3}\),\(BC=1\),如下图所示,

则在直角\(△OBC\)中,\(\left|\overrightarrow{v_{1}}\right|=O B=\sqrt{O C^{2}+B C^{2}}=2\),\(\tan \angle B O C=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
又\(\angle A O C \in\left(0, \dfrac{\pi}{2}\right)\),所以\(\angle B O C=\dfrac{\pi}{6}\),
则\(\beta=\dfrac{\pi}{2}+\dfrac{\pi}{6}=\dfrac{2 \pi}{3}\),
答 (1)他实际前进方向与水流方向的夹角\(α\)为\(\dfrac{\pi}{3}\),\(v_2\)的大小为\(2m/s\);
(2)他游泳的方向与水流方向的夹角\(β\)为\(\dfrac{2\pi}{3}\),\(v_1\)的大小为\(2m/s\).
【点拨】 注意平行四边形法则的使用!
【典题2】 在日常生活中,我们会看到如图所示的情境,两个人共提一个行李包.假设行李包所受重力为\(G\),作用在行李包上的两个拉力分别为\(\overrightarrow{F_{1}}, \overrightarrow{F_{2}}\),且\(\left|\overrightarrow{F_{1}}\right|=\left|\overrightarrow{F_{2}}\right|\),\(\overrightarrow{F_{1}}\)与\(\overrightarrow{F_{2}}\)的夹角为\(θ\).给出以下结论
①\(θ\)越大越费力,\(θ\)越小越省力;
②\(θ\)的范围为\([0 ,π]\);
③当\(\theta=\dfrac{\pi}{2}\)时,\(\left|\overrightarrow{F_{1}}\right|=\mid \vec{G}|\);
④当\(\theta=\dfrac{2 \pi}{3}\)时,\(\left|\overrightarrow{F_{1}}\right|=|\vec{G}|\).
其中正确结论的序号是 .

【解析】 对于①,由\(|\vec{G}|=\left|\overrightarrow{F_{1}}+\overrightarrow{F_{2}}\right|\)为定值,
所以\({G}^{2}=\left|\overrightarrow{F_{1}}\right|^{2}+\left|\overrightarrow{F_{2}}\right|^{2}+2\left|\overrightarrow{F_{1}}\right| \times\left|\overrightarrow{F_{2}}\right| \times \cos \theta\)\(=2\left|\overrightarrow{F_{1}}\right|^{2}(1+\cos \theta) .\),
解得\(\left|\overrightarrow{F_{1}}\right|^{2}=\dfrac{|\vec{G}|^{2}}{2(1+\cos \theta)}\);
由题意知\(θ∈(0 ,π)\)时,\(y=cosθ\)单调递减,所以\(\left|\overrightarrow{F_{1}}\right|^{2}\)单调递增,
即\(θ\)越大越费力,\(θ\)越小越省力;①正确.
对于②,由题意知,\(θ\)的取值范围是\((0 ,π)\),所以②错误.
对于③,当\(\theta=\dfrac{\pi}{2}\)时,\(\left|\overrightarrow{F_{1}}\right|^{2}=\dfrac{\vec{G}^{2}}{2}\),所以\(\left|\overrightarrow{F_{1}}\right|=\dfrac{\sqrt{2}}{2}|\vec{G}|\),③错误.
对于④,当\(\theta=\dfrac{2 \pi}{3}\)时,\(\left|\overrightarrow{F_{1}}\right|^{2}=|\vec{G}|^{2}\),所以\(\left|\overrightarrow{F_{1}}\right|=|\vec{G}|\),④正确.
综上知,正确结论的序号是①④.
故答案为 ①④.
【典题3】 如图,重为\(10N\)的匀质球,半径\(R\)为\(6cm\),放在墙与均匀的\(AB\)木板之间,\(A\)端锁定并能转动,\(B\)端用水平绳索\(BC\)拉住,板长\(AB=20cm\),与墙夹角为\(α\),如果不计木板的重量,则\(α\)为何值时,绳子拉力最小?最小值是多少?

【解析】 如图,设木板对球的支持力为\(\vec{N}\),则\(\vec{N}=\dfrac{10}{\sin \alpha}\),
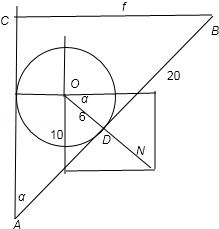
设绳子的拉力为\(\vec{f}\).又\(AC=20\cosα\),\(A D=\dfrac{6}{\tan \dfrac{\alpha}{2}}\),
由动力矩等于阻力矩得\(|\vec{f}| \times 20 \cos \alpha=|\vec{N}| \times \dfrac{6}{\tan \dfrac{\alpha}{2}}\)\(=\dfrac{60}{\sin \alpha \cdot \tan \dfrac{\alpha}{2}}\)
\(\therefore|\vec{f}|=\dfrac{60}{20 \cos \alpha \cdot \sin \alpha \cdot \tan \dfrac{\alpha}{2}}\)\(=\dfrac{3}{\cos \alpha(1-\cos \alpha)} \geq \dfrac{3}{\left(\dfrac{\cos \alpha+1-\cos \alpha}{2}\right)^{2}}=\dfrac{3}{\dfrac{1}{4}}=12\),
\(∴\)当且仅当\(\cos \alpha=1-\cos \alpha\)即\(\cos \alpha=\dfrac{1}{2}\),
亦即\(α=60°\)时,\(|\vec{f}|\)有最小值\(12N\).
巩固练习
1(★★)一条渔船以\(6km/h\)的速度向垂直于对岸的方向行驶,同时河水的流速为\(2km/h\),则这条渔船实际航行的速度大小为\(\underline{\quad \quad}\).
2(★★)如图所示,一个物体被两根轻质细绳拉住,且处于平衡状态,已知两条绳上的拉力分别是\(F_1\),\(F_2\),且\(F_1\),\(F_2\)与水平夹角均为\(45°\),\(\left|\vec{F}_{1}\right|=\left|\vec{F}_{2}\right|=10 \sqrt{2} N\),则物体的重力大小为\(\underline{\quad \quad}\).

3(★★)用向量方法证明 对角线互相垂直的平行四边形是菱形.
4(★★)证明勾股定理,在\(Rt∆ABC\)中,\(AC⊥BC\),\(AC=b\),\(BC=a\),\(AB=c\),则\(c^2=a^2+b^2\).
5(★★)已知一艘船以\(5km/h\)的速度向垂直于对岸方向行驶,航船实际航行方向与水流方向成\(30°\)角,求水流速度和船实际速度.
6(★★)一个物体受到同一平面内三个力\(F_1\)、\(F_2\)、\(F_3\)的作用,沿北偏东\(45°\)的方向移动了\(8m\).已知\(|F_1 |=2N\),方向为北偏东\(30°\);\(|F_2 |=4N\),方向为东偏北\(30°\);\(|F_3 |=6N\),方向为西偏北\(60°\),求这三个力的合力\(F\)所做的功.
参考答案
1.\(2 \sqrt{10} \mathrm{~km} / \mathrm{h}\)
2.\(20\)
3. 证明略
4. 证明略
5. 船实际航行速度的大小为\(10km/h\),水流速度\(5 \sqrt{3} \mathrm{~km} / \mathrm{h}\)
6.\(24 \sqrt{6}\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号