专题 求数列的通项公式
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【【高分突破系列】 高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第二册同步提高,难度3颗星!
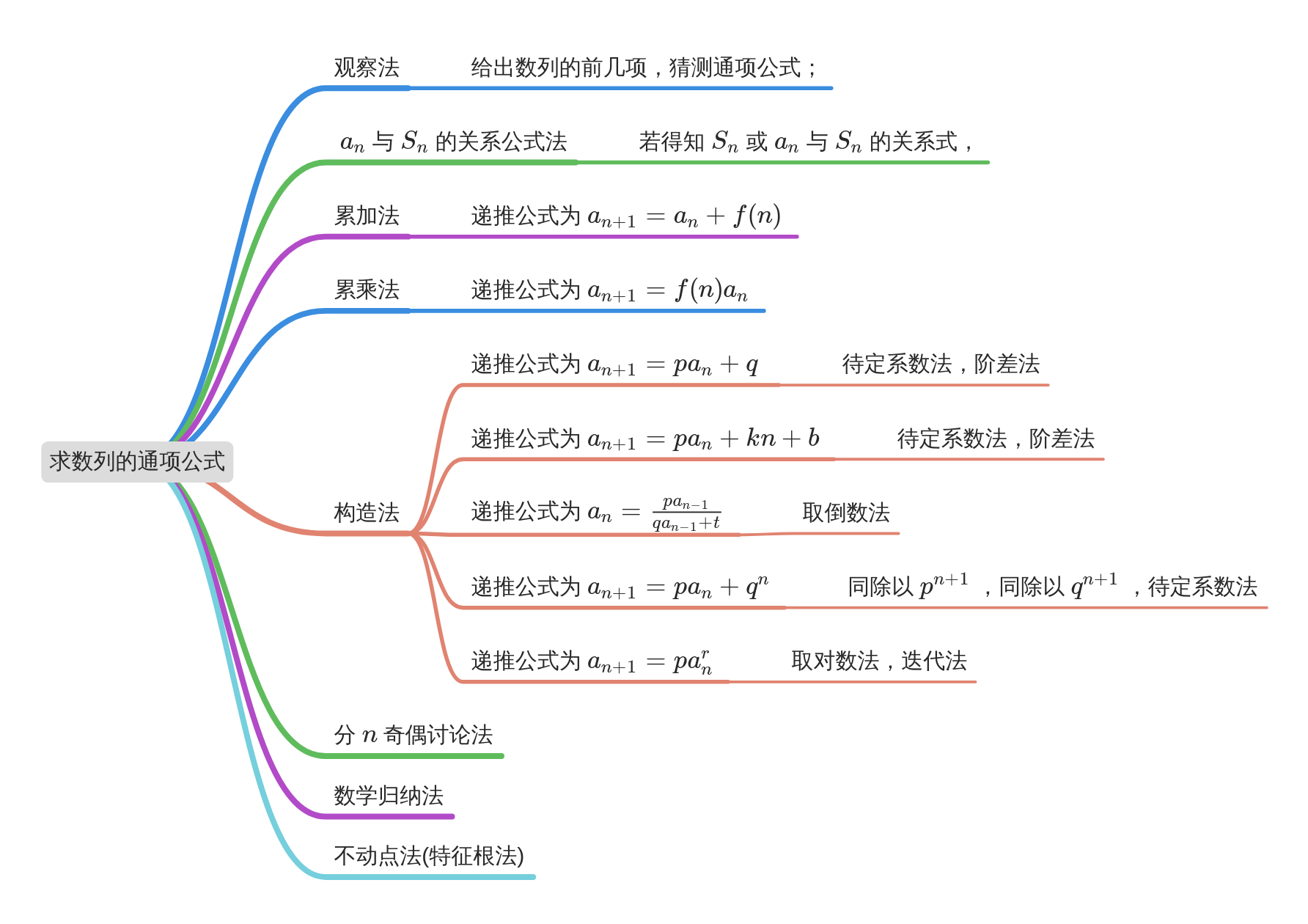
模块导图
知识剖析
求数列的通项公式是高考常考的一专题,形式多样,解题方法很多,常见的有累加法、累乘法、待定系数法、迭代法、取倒数法等,课外延申的还有不动点法等,不管什么方法,一定要理解解题方法的本质,清楚每种方法的适用范围,避免出现“看得懂,模仿做还行,独立思考就含糊”的情况.
经典例题
【方法一】观察法
\({\color{Red}{适用范围:}}\)给出数列的前几项,猜测通项公式;
\({\color{Red}{方法:}}\)通过观察,得知数列各项之间数值的关系(比如数值之间的差或商成一定规律)或数值结构特点(比如数值的正负,分式,平方)从而求得通项公式.
【典题1】写出下列数列\(\{a_n\}\)的一个通项公式
\((1)-7,14,-21,28,…\)
\((2) \dfrac{1}{4}, \dfrac{3}{8}, \dfrac{5}{16}, \dfrac{7}{32} \ldots\)
\((3) 2,5,10,17,26,…\)
\((4) 32,332,3332,33332,….\)
\((5) 1,2,2,3,3,4,4,….\)
【解析】\({\color{Red}{分解结构法:}}\)注意数值的结构,看其是否可视为两个或多个数列组合而成.
\((1)\)数列\(-7 ,14 ,-21 ,28\),…每项可分解成符号和项的绝对值相乘得到,
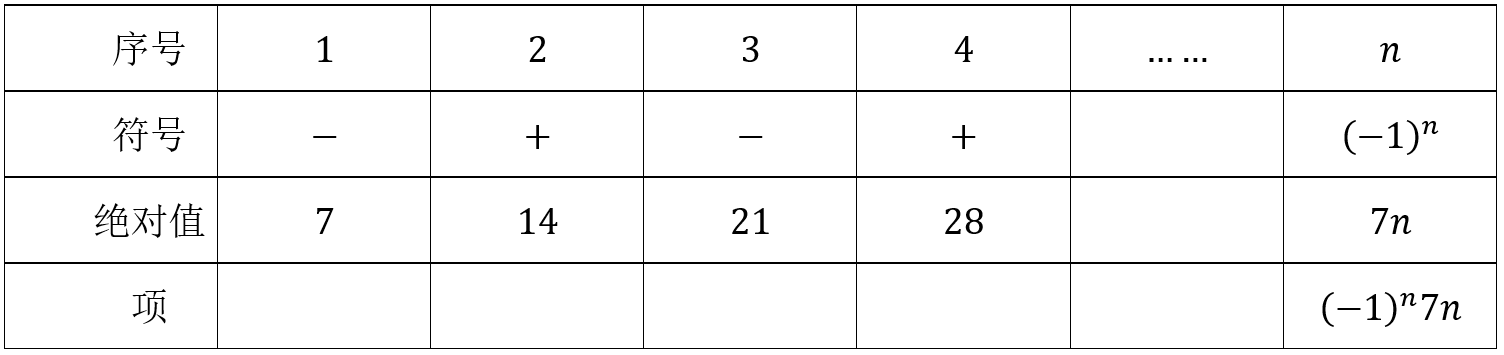
故\(a_{n}=(-1)^{n} 7 n\);
\((2)\)数列\(\dfrac{1}{4}, \dfrac{3}{8}, \dfrac{5}{16}, \dfrac{7}{32} \ldots\)…每项可分解成分子和分母相除得到,
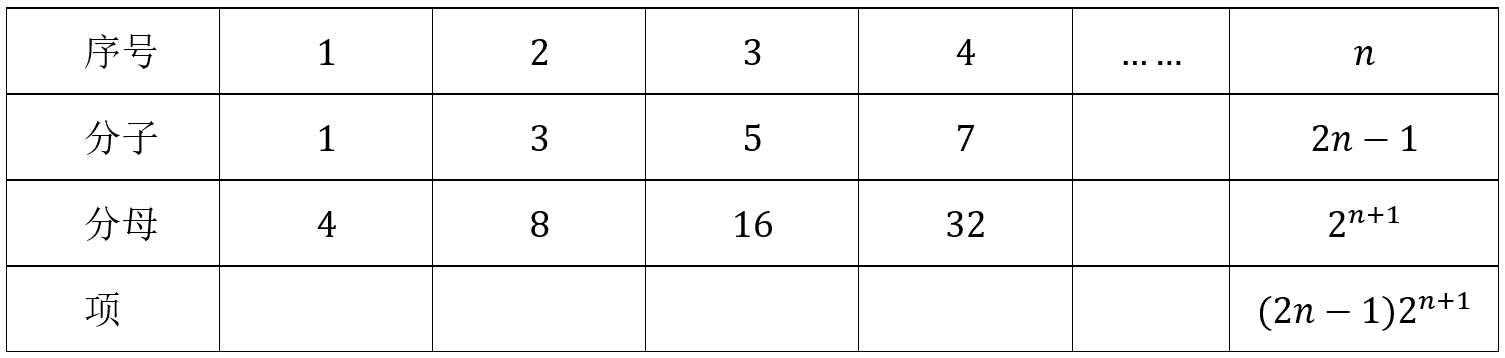
故\(a_n=(2n-1)2^{n+1}\);
\({\color{Red}{变形法:}}\)数列本身特点不明显,但通过加减乘除某个数之类方式变形成“规律感更强”的数列.
\((3)\)数列\(2 ,5 ,10 ,17 ,26\),…中若每项减去\(1\),则变成\(1\),\(4\),\(9\),\(16\),\(25\),…,
这些数都是完全平方数,易想到数列的通项是\(n^2\),
则原数列只需要在这基础上加回\(1\)便可,即\(a_n=n^2+1\).
\((4)\)数列\(2\),\(32\),\(332\),\(3332\),\(33332\),….中若每项加上\(1\),则变成\(3\),\(33\),\(333\),\(3333\),\(33333\),….,再每项乘以\(3\),变成\(9\),\(99\),\(999\),\(9999\),\(99999\),…
其中\(9=10-1\),\(99=10^2-1\),\(999=10^3-1\),\(9999=10^4-1\),\(99999=10^5-1\),
则其通项\(b_n=10^{n+1}-1\),
要求原数列的通项公式,
则“逆回去”,除以\(3\)再减\(1\)可得\(a_{n}=\dfrac{b_{n}}{3}-1=\dfrac{10^{n+1}-1}{3}-1=\dfrac{10^{n+1}-4}{3}\).
\({\color{Red}{分奇偶项}}\)
\((5)\)数列\(1\),\(2\),\(2\),\(3\),\(3\),\(4\),\(4\),… , 相邻每项之间没什么关系,若分奇偶性来看,就简单多了,
可得奇数项为\(1\),\(2\),\(3\),\(4\),… , 可得\(a_{n}=\dfrac{n+1}{2}\).偶数项为\(2\),\(3\),\(4\),… , 可得\(a_{n}=\dfrac{n+2}{2}\).
则该数列通项公式\(a_{n}= \begin{cases}\dfrac{n+1}{2}, & n \text { 为奇数 } \\ \dfrac{n+2}{2}, & n \text { 为偶数 }\end{cases}\).
【点拨】观察法主要是依靠“数感”,以上讲解的“分解结构法”“变形法”可有助于观察,它对后面讲到的利用数学归纳法求解通项公式有用.
巩固练习
1 (★)数列\(1,-\dfrac{\sqrt{2}}{2}, \dfrac{1}{2},-\dfrac{\sqrt{2}}{4}, \dfrac{1}{4}\), …的一个通项公式为( )
A.\(\left(-\dfrac{1}{2}\right)^{n-1}\) \(\qquad \qquad\) B.\(\left(-\dfrac{\sqrt{2}}{2}\right)^{n}\) \(\qquad \qquad\) C.\((-1)^{n}\left(\dfrac{\sqrt{2}}{2}\right)^{n-1}\) \(\qquad \qquad\) D.\((-1)^{n+1}\left(\dfrac{\sqrt{2}}{2}\right)^{n-1}\)
2 (★)下列可作为数列\(1\),\(2\),\(1\),\(2\),\(1\),\(2\),…的通项公式的是( )
A.\(a_{n}=\dfrac{1+(-1)^{n-1}}{2}\) \(\qquad \qquad\)B.\(a_{n}=\dfrac{3+(-1)^{n}}{2}\) \(\qquad \qquad\) C.\(a_{n}=2-\sin \dfrac{n \pi}{2}\) \(\qquad \qquad\) D.\(a_{n}=2-\cos [(n-1) \pi]\)
3 (★★)写出以下各数列的一个通项公式.
\((1)1,-\dfrac{1}{2}, \dfrac{1}{4},-\dfrac{1}{8}, \ldots\)
\((2)10 ,9 ,8 ,7 ,6 ,…\)
\((3)0 ,3 ,8 ,15 ,24 ,…\)
\((4) \dfrac{1}{2}, \dfrac{5}{6}, \dfrac{11}{12}, \dfrac{19}{20}, \dfrac{31}{30}\)
\((5)4 ,44 ,444 ,4444 ,….\)
参考答案
1.\(D\)
2.\(B\)
3.\((1) a_{n}=(-1)^{n+1} \times \dfrac{1}{2^{n-1}}\)
\((2) a_n=11-n\)
\((3) a_n=n^2-1\)
\((4)a_{n}=1-\dfrac{1}{n(n+1)}\)
\((5) a_{n}=\dfrac{4}{9} \times\left(10^{n}-1\right)\).
【方法二】\(a_n\)与\(S_n\)的关系公式法
\({\color{Red}{适用范围:}}\)若得知\(S_n\)或\(a_n\)与\(S_n\)的关系式,求数列通项公式.
\({\color{Red}{方法:}}\)利用\(a_n\)与\(S_n\)的关系\(a_{n}=\left\{\begin{array}{cc}
S_{1} & n=1 \\
S_{n}-S_{n-1} & n \geq 2
\end{array}\right.\),注意分类讨论,最后确定\(a_1\)是否满足\(a_n=f(n)\)\((n≥2)\).
【典题1】已知数列\(\{a_n\}\)的前\(n\)项和\(S_n\),满足关系\(\lg \left(S_{n}+1\right)=n\).求\(\{a_n\}\)的通项公式.
【解析】\(\because \lg \left(S_{n}+1\right)=n\),
\(\therefore S_{n}=10^{n}-1\)
当\(n≥2\)时,\(a_{n}=S_{n}-S_{n-1}=9 \times 10^{n-1}\)
当\(n=1\)时,\(a_1=S_1=9\)满足\(a_{n}=9 \times 10^{n-1}\),
\({\color{Red}{ (确定a_1是否满足上式)}}\)
\(\therefore a_{n}=9 \times 10^{n-1}\left(n \in N^{*}\right)\).
\({\color{Red}{(最后等式才由n≥2变成n∈N^*)}}\)
【典题2】已知数列\(\{a_n\}\)}的前\(n\)项和\(S_n\),\(a_1=1\),满足下列条件
①\(∀n∈N^*\),\(a_n>0\);\(\qquad \qquad\) ②点\((a_n ,S_n)\)在函数\(f(x)=\dfrac{x^{2}+x}{2}\)的图象上;
求数列\(\{a_n\}\)的通项\(a_n\)及前\(n\)项和\(S_n\).
【解析】由题意\(S_{n}=\dfrac{a_{n}^{2}+a_{n}}{2}\),
当\(n≥2\)时,\(a_{n}=S_{n}-S_{n-1}=\dfrac{a_{n}^{2}+a_{n}}{2}-\dfrac{a_{n-1}^{2}+a_{n-1}}{2}\),
整理,得\(\left(a_{n}+a_{n-1}\right)\left(a_{n}-a_{n-1}-1\right)=0\),
\({\color{Red}{(因式分解)}}\)
又\(∀n∈N^*\),\(a_n>0\),所以\(a_{n}+a_{n-1} \neq 0\)
即\(a_{n}-a_{n-1}=1\),
又\(a_1=1\),
\(∴\)数列\(\{a_n\}\)是首项为\(1\),公比为\(1\)的等差数列,
\(∴a_n=n\),\(S_{n}=\dfrac{n^{2}+n}{2}\).
【典题3】已知\(\{a_n\}\)中,\(a_1=1\),\(a_{n}=\dfrac{2 S_{n}^{2}}{2 S_{n}-1}\)\((n≥ 2)\),求\(a_n\).
【解析】当\(n≥2\)时,\(a_{n}=S_{n}-S_{n-1}\)
\(\therefore S_{n}-S_{n-1}=\dfrac{2 S_{n}^{2}}{2 S_{n}-1}\)
\(\therefore S_{n-1}-S_{n}=2 S_{n} S_{n-1}\)
两边同除以\(S_{n} S_{n-1}\),得\(\dfrac{1}{S_{n}}-\dfrac{1}{S_{n-1}}=2\)
\({\color{Red}{ (该变式技巧了解下)}}\)
\({\color{Red}{ (上两题是“消去”S_n得到数列\{a_n\}递推公式,该题“消去”a_n得到数列\{S_n\}的递推公式)}}\)
\(∴\)数列\(\left\{\dfrac{1}{S_{n}}\right\}\)为等差数列,公差为\(2\),首项为\(1\).
\(\therefore \dfrac{1}{S_{n}}=1+2(n-1)=2 n-1\),
解得\(S_{n}=\dfrac{1}{2 n-1}\),
\(\therefore a_{n}=S_{n}-S_{n-1}=\dfrac{1}{2 n-1}-\dfrac{1}{2 n-3}=\dfrac{-2}{(2 n-1)(2 n-3)}\)\((n≥ 2)\)
\({\color{Red}{(不要漏了大前提n≥ 2)}}\)
\(a_1=1\)不满足\(a_{n}=\dfrac{-2}{(2 n-1)(2 n-3)}\),
\(\therefore a_{n}= \begin{cases}1, & n=1 \\ \dfrac{-2}{(2 n-1)(2 n-3)}, & n \geq 2\end{cases}\).
【点拨】当题中得知\(S_n\)或\(a_n\)与\(S_n\)的关系式,则可利用公式\(a_{n}=\left\{\begin{array}{cc}
S_{1} & n=1 \\
S_{n}-S_{n-1} & n \geq 2
\end{array}\right.\),消去\(a_n\)与\(S_n\),得到对应的递推公式进而求解\(a_n\),但最后都要注意确定\(a_1\)是否满足\(a_n=f(n)(n≥2)\).
巩固练习
1 (★)已知数列\(\{a_n\}\)的前\(n\)项和\(S_n\)满足\(S_n=n^2+n-1\),求数列\(\{a_n\}\)的通项公式.
2 (★★)已知无穷数列\(\{a_n\}\)的前\(n\)项和\(S_n\),并且\(a_n+S_n=1\),求\(\{a_n\}\)的通项公式.
3 (★★)已知数列\(\{a_n\}\)的前\(n\)项和\(S_n\),满足\(a_2=-4\),\(2 S_{n}=n\left(a_{n}-7\right)\).求\(a_1\)和数列\(\{a_n\}\)的通项公式;
4 (★★★)设数列\(\{a_n\}\)的前\(n\)项和\(S_n\),已知\(a_1=2\),\(a_2=8\),\(S_{n+1}+4 S_{n-1}=5 S_{n}(n \geq 2)\),求数列\(\{a_n\}\)的通项公式;
参考答案
1.\(a_{n}=\left\{\begin{array}{c}
1, n=1 \\
2 n, n \geq 2
\end{array}\right.\)
2.\(a_{n}=\left(\dfrac{1}{2}\right)^{n}\)
3.\(a_1=-7\),\(a_n=3n-10(n∈N^*)\)
4.\(a_{n}=2^{2 n-1}\)
【方法三】累加法
\({\color{Red}{适用范围:}}\)递推式为\(a_{n+1}=a_{n}+f(n)\).
\({\color{Red}{方法:}}\)得到\(\rfloor a_{n+1}-a_{n}=f(n)\),利用累加的形式求出\(a_n\).
【典题1】已知数列\(\{a_n\}\)满足\(a_1=2\),\(a_{n+1}=a_{n}+\ln \left(1+\dfrac{1}{n}\right)\),求\(a_n\).
【解析】由条件知:\(a_{n+1}-a_{n}=\ln \left(1+\dfrac{1}{n}\right)=\ln \dfrac{n+1}{n}=\ln (n+1)-\ln n\)
\(∴n≥2\)时
\(\left\{\begin{aligned}
a_{n}-a_{n-1} &=\ln n-\ln (n-1) \\
a_{n-1}-a_{n-2} &=\ln (n-1)-\ln (n-2) \\
a_{4}-a_{3} &=\ln 4-\ln 3 \\
a_{3}-a_{2} &=\ln 3-\ln 2 \\
a_{2}-a_{1} &=\ln 2-\ln 1
\end{aligned}\right.\),
把以上\(n-1\)个式子累加得\(a_{n}-a_{1}=\ln n-\ln 1=\ln n\),
\(\therefore a_{n}=a_{1}+\ln n=\ln n+2 \quad(n \geq 2)\),
\(a_1=2\)也满足\(a_{n}=\ln n+2\),
\(\therefore a_{n}=\ln n+2 \quad\left(n \in N^{*}\right)\).
【典题2】已知数列\(\{a_n\}\)满足\(a_{n+1}=a_{n}+2 \times 3^{n}+1\),\(a_1=3\),求数列\(\{a_n\}\)的通项公式.
【解析】由\(a_{n+1}=a_{n}+2 \times 3^{n}+1\)得\(a_{n+1}-a_{n}=2 \times 3^{n}+1\)
\(∴n≥2\)时,
\(\begin{aligned}
&a_{n}=\left(a_{n}-a_{n-1}\right)+\left(a_{n-1}-a_{n-2}\right)+\cdots+\left(a_{3}-a_{2}\right)+\left(a_{2}-a_{1}\right)+a_{1} \\
&=\left(2 \times 3^{n-1}+1\right)+\left(2 \times 3^{n-2}+1\right)+\cdots+\left(2 \times 3^{2}+1\right)+\left(2 \times 3^{1}+1\right)+3 \\
&=2\left(3^{n-1}+3^{n-2}+\cdots+3^{2}+3^{1}\right)+(n-1)+3 \\
&=2 \dfrac{3\left(1-3^{n-1}\right)}{1-3}+(n-1)+3 \\
&=3^{n}+n-1
\end{aligned}\)
而\(a_1=3\)也满足\(a_n=3^n+n-1\),
\(∴a_n=3^n+n-1 (n∈N^*)\).
巩固练习
1 (★)数列\(\{a_n\}\)满足\(a_1=3\),\(a_{n+1}-a_{n}=2 n-8\left(n \in N^{*}\right)\),则\(a_8=\)\(\underline{\quad \quad }\).
2 (★★)将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第\(20\)行从左至右的第\(3\)个数是 \(\underline{\quad \quad}\) .

3 (★★)已知数列\(\{a_n\}\)满足\(a_{1}=\dfrac{1}{2}\),\(a_{n+1}=a_{n}+\dfrac{1}{n^{2}+n}\),求\(a_n\)
4 (★★★)已知数列\(\{a_n\}\)的前\(n\)项和\(S_n\),\(S_n+a_n=n+2\),\(n∈N^*\).
(1)证明:数列\(\left\{a_{n}-1\right\}\)为等比数列;
(2)若数列\(\left\{b_{n}\right\}\)满足\(a_{n}=b_{n+1}-b_{n}+1\),\(b_1=1\),证明:\(b_n<2\).
参考答案
1.\(3\)
2.\(577\)
3.\(a_{n}=\dfrac{3}{2}-\dfrac{1}{n}\)
4.\((1)\)提示:定义法证明
\((2)\)提示:累加法求\(b_{n}=2-\dfrac{1}{2^{n}-1}\)
【方法四】累乘法
\({\color{Red}{适用范围:}}\)递推式为\(a_{n+1}=f(n) a_{n}\).
\({\color{Red}{方法:}}\)得到\(\dfrac{a_{n+1}}{a_{n}}=f(n)\),利用累乘的形式求出\(a_n\).
【典题1】已知\(\{a_n\}\)中,满足\(a_1=1\),\(a_{n}=a_{1}+2 a_{2}+3 a_{3}+\cdots+(n-1) a_{n-1}(n \geq 2)\),求\(a_n\).
【解析】由已知,得\(a_{n+1}=a_{1}+2 a_{2}+3 a_{3}+\cdots+(n-1) a_{n-1}+n a_{n}\),
用此式减去已知式,得
当\(n≥ 2\)时,\(a_{n+1}-a_{n}=n a_{n}\),
即\(a_{n+1}=(n+1) a_{n} \Rightarrow \dfrac{a_{n+1}}{a_{n}}=n+1\),
又\(a_2=a_1=1\),
\(\therefore\left\{\begin{array}{c}
\dfrac{a_{n}}{a_{n-1}}=n \\
\dfrac{a_{n-1}}{a_{n-2}}=n-1 \\
\dfrac{a_{3}}{a_{2}}=3 \\
\dfrac{a_{2}}{a_{1}}=2
\end{array}\right.\),
将以上\(n-1\)个式子相乘,得\(\dfrac{a_{n}}{a_{1}}=\dfrac{n !}{2} (n≥ 2)\),
\(\therefore a_{n}=\dfrac{n !}{2} \quad(n \geq 2)\),
\(\therefore a_{n}= \begin{cases}1, & n=1 \\ \dfrac{n !}{2}, & n \geq 2\end{cases}\).
【典题2】设数列\(\{a_n\}\)是首项为1的正项数列,且\((n+1) a_{n+1}^{2}-n a_{n}^{2}+a_{n+1} a_{n}=0\), 求通项公式\(a_n\)
【解析】由\((n+1) a_{n+1}^{2}-n a_{n}^{2}+a_{n+1} a_{n}=0\),
可得\(n\left(a_{n+1}^{2}-a_{n}^{2}\right)+\left(a_{n+1}^{2}+a_{n+1} a_{n}\right)=0\),
即有\(n\left(a_{n+1}-a_{n}\right)\left(a_{n+1}+a_{n}\right)+a_{n+1}\left(a_{n+1}+a_{n}\right)=0\),
即有\(\left[(n+1) a_{n+1}-n a_{n}\right]\left(a_{n+1}+a_{n}\right)=0\)
由\(\{a_n\}\)是正项数列,可得\((n+1) a_{n+1}=n a_{n} \Rightarrow a_{n+1}=\dfrac{n}{n+1} a_{n}\),
则\(a_{n}=\dfrac{n-1}{n} a_{n-1}=\dfrac{n-1}{n} \cdot \dfrac{n-2}{n-1} a_{n-2}\)\(=\cdots=\dfrac{n-1}{n} \cdot \dfrac{n-2}{n-1} \cdots \dfrac{2}{3} \cdot \dfrac{1}{2} a_{1}\)\(=\dfrac{1}{n} a_{1}=\dfrac{1}{n}(n \geq 2)\),
\(a_1=1\)也满足\(a_{n}=\dfrac{1}{n}\),
\(∴a_{n}=\dfrac{1}{n},n∈N^*\).
巩固练习
1 (★★)已知数列\(a_1\),\(\dfrac{a_{2}}{a_{1}}\),\(\dfrac{a_{3}}{a_{2}}\),⋯,\(\dfrac{a_{n}}{a_{n-1}}\)是首项为\(8\),公比为\(\dfrac{1}{2}\)的等比数列,则\(a_4\)等于\(\underline{\quad \quad }\).
2 (★★)在数列\(\{a_n\}\)中,\(a_1=a_2=1\),\(a_3=2\),且数列\(\left\{\dfrac{a_{n+1}}{a_{n}}\right\}\)为等比数列,则\(a_n=\)\(\underline{\quad \quad }\).
3 (★★)已知\(a_1=3\),\(a_{n+1}=\dfrac{3 n-1}{3 n+2} a_{n}(n \geq 1)\),求\(a_n\).
4 (★★)已知\(a_1=1\),\(a_{n}=n(a_{n+1}-a_{n})(n\in N^*)\),求数列\(\{a_n\}\)通项公式.
参考答案
1.\(64\)
2.\(2^{\dfrac{(n-2)(n-1)}{2}}\)
3.\(a_{n}=\dfrac{6}{3 n-1}\)
4.\(a_n=n\)
【方法五】构造法
对于一些不是等差等比数列的数列,求其通项公式,通过构造等差或等比数列来求其通项公式是一种很好的思路,其中的情况多样,方法有待定系数法、阶差法、取倒数法、取对数法等.我们要理解其中构造的技巧,做到举一反三.
情况1
递推公式为\(a_{n+1}=p a_{n}+q\)(\(p\),\(q\)为常数,\(p≠1\),\(pq≠0\))
\({\color{Red}{待定系数法:}}\)把原递推公式转化为:\(a_{n+1}+t=p\left(a_{n}+t\right)\),其中\(t=\dfrac{q}{p-1}\),再利用换元法转化为等比数列\(\left\{a_{n}+t\right\}\)求解;
\({\color{Red}{逐项相减法(阶差法):}}\)由\(a_{n+1}=p a_{n}+q\)得\(a_{n}=p a_{n-1}+q\),两式相减得\(a_{n+1}-a_{n}=p\left(a_{n}-a_{n-1}\right)\),即\(\left\{a_{n+1}-a_{n}\right\}\)是等比数列,再用累加法求解.
【典题1】已知数列\(\{a_n\}\)中,\(a_1=1\),\(a_{n+1}=2 a_{n}+3\), 求\(a_n\).
【解析】\({\color{Red} {方法一\quad 待定系数法}}\)
设递推公式\(a_{n+1}=2 a_{n}+3\)可以转化为\(a_{n+1}+t=2\left(a_{n}+t\right)\)(\(t\)是个常数),
即\(a_{n+1}=2 a_{n}+t\),
与已知条件\(a_{n+1}=2 a_{n}+3\)比较可知\(t=3\),
\({\color{Red}{ (比较系数可求参数t )}}\)
故递推公式为\(a_{n+1}+3=2\left(a_{n}+3\right)\),
所以\(\left\{a_{n}+3\right\}\)是首项为\(a_1+3=4\),公比为\(2\)的等比数列,
\({\color{Red}{ (构造等比数列)}}\)
则\(a_{n}+3=4 \times 2^{n-1}=2^{n+1}\),
\(\therefore a_{n}=2^{n+1}-3\).
\({\color{Red}{方法二 \quad 逐项相减法}}\)
\(\because a_{n+1}=2 a_{n}+3\),\(\therefore a_{n}=2 a_{n-1}+3\)
两式相减得\(a_{n+1}-a_{n}=2\left(a_{n}-a_{n-1}\right)(n \geq 2)\)
\(∴\)数列\(\left\{a_{n+1}-a_{n}\right\}\)是以\(a_2-a_1=5-1=4\)为首项,公比\(q=2\)的等比数列, \({\color{Red}{(构造等比数列)}}\)
\(\therefore a_{n+1}-a_{n}=2^{n+1}\),
\({\color{Red}{(形如a_{n+1}-a_{n}=f(n)用累加法)}}\)
\(\therefore a_{n+1}=\left(a_{n+1}-a_{n}\right)+\left(a_{n}-a_{n-1}\right)+\cdots\left(a_{2}-a_{1}\right)+a_{1}\)\(=2^{n+1}+2^{n}+\cdots+4+1=2^{n+2}-3\)
\(\therefore a_{n}=2^{n+1}-3\).
情况2
递推公式为\(a_{n+1}=p a_{n}+k n+b\)(\(p\),\(k\),\(b\)为常数,\(p≠1\),\(pk≠0\))
\({\color{Red}{待定系数法:}}\) \(a_{n+1}=p a_{n}+k n+b\)可化为\(a_{n+1}+\lambda_{1}(n+1)+\lambda_{2}=A\left[a_{n}+\lambda_{1} n+\lambda_{2}\right]\)的形式,得到等比数列\(\left\{a_{n}+\lambda_{1} n+\lambda_{2}\right\}\)求出\(a_n\).
\({\color{Red}{逐项相减法(阶差法):}}\)由\(a_{n+1}=p a_{n}+k n+b\)得\(a_{n}=p a_{n-1}+k(n-1)+b\),两式相减得\(a_{n+1}-a_{n}=p\left(a_{n}-a_{n-1}\right)+k\),即令\(b_{n}=a_{n+1}-a_{n}\)得\(b_{n}=p b_{n-1}+k\),再用递推公式形如\(a_{n+1}=p a_{n}+q\)的方法求解.
【典题1】设数列\(\{a_n\}\):\(a_1=4\),\(a_{n}=3 a_{n-1}+2 n-1(n \geq 2)\),求\(a_n\).
【解析】\({\color{Red}{方法一 \quad 待定系数法}}\)
令\(a_{n}+\lambda_{1} n+\lambda_{2}=3\left[a_{n-1}+\lambda_{1}(n-1)+\lambda_{2}\right]\)
化简得:\(a_{n}=3 a_{n-1}+2 \lambda_{1} n+2 \lambda_{2}-3 \lambda_{1}\)
与已知条件\(a_{n}=3 a_{n-1}+2 n-1\)比较系数,
所以\(\left\{\begin{array}{c}
2 \lambda_{1}=2 \\
2 \lambda_{2}-3 \lambda_{1}=-1
\end{array}\right.\), 解得\(\left\{\begin{array}{l}
\lambda_{1}=1 \\
\lambda_{2}=1
\end{array}\right.\),
\({\color{Red}{ (比较系数可求参数λ_1,λ_2)}}\)
所以\(a_{n}+n+1=3\left(a_{n-1}+n\right)\)
\(∴\)数列\(\left\{a_{n}+n+1\right\}\)是以\(a_1+2=6\)为首项,\(3\)为公比的等比数列.
\(\therefore a_{n}+n+1=6 \times 3^{n-1}=2 \times 3^{n}\),
\(∴a_n=2×3^n-n-1\).
\({\color{Red}{方法二 \quad 逐项相减法(阶差法)}}\)
\(\because a_{n}=3 a_{n-1}+2 n-1(n \geq 2)\)①
\(\therefore a_{n+1}=3 a_{n}+2 n+1\)②
由②-①得\(a_{n+1}-a_{n}=3\left(a_{n}-a_{n-1}\right)+2\)
令\(b_{n}=a_{n+1}-a_{n}\),则\(b_{n}=3 b_{n-1}+2\)
\({\color{Red}{ (回归递推公式形如a_{n}=p a_{n-1}+q的形式)}}\)
\(\therefore b_{n}+1=3\left(b_{n-1}+1\right)\)
\(∴\)数列\(\left\{b_{n}+1\right\}\)是以首项\(b_1+1=a_2-a_1+1=15-4+1=12\),公比\(q=3\)的等比数列,
则\(b_{n}+1=12 \times 3^{n-1}=4 \times 3^{n} \Rightarrow b_{n}=4 \times 3^{n}-1\)
\(\therefore a_{n+1}=\left(a_{n+1}-a_{n}\right)+\left(a_{n}-a_{n-1}\right)+\cdots\left(a_{2}-a_{1}\right)+a_{1}\) \({\color{Red}{(累加法)}}\)
\(=\left(4 \times 3^{n}-1\right)+\left(4 \times 3^{n-1}-1\right)+\cdots+\left(4 \times 3^{1}-1\right)+4\)
\(=2 \times 3^{n+1}-n-2\)
\(∴a_n=2×3^n-n-1\).
【点拨】二种方法比较还是待定系数法过程显得简洁些,形如\(a_{n+1}=p a_{n}+q\)和\(a_{n+1}=p a_{n}+k n+b\)都可用待定系数法构造等比数列来求\(a_n\),那是否形如\(a_{n+1}=p a_{n}+f(n)\)都可行呢?那形如“\(a_{n+1}=p a_{n}+\)二次函数”如何?试试题目:已知\(a_1=6\),\(a_{n+1}=2 a_{n}-n^{2}+n+2\),求\(a_n\).(答案:\(a_{n}=2^{n+1}+n^{2}+n\)).
情况3
递推公式为\(a_{n}=\dfrac{p a_{n-1}}{q a_{n-1}+t}\)(\(p\),\(q\),\(t\)为常数)
\({\color{Red}{取倒数法:}}\)递推公式两边取倒数,\(\dfrac{1}{a_{n}}=\dfrac{q a_{n-1}+t}{p a_{n-1}}=\dfrac{q}{p}+\dfrac{t}{p} \cdot \dfrac{1}{a_{n-1}}\),令\(b_{n}=\dfrac{1}{a_{n}}\),若\(p=t\),则问题\(b_n\)是等差数列;若\(p≠t\),问题转化为递推公式为:\(a_{n+1}=p_{1} a_{n}+q_{1}\)的方法处理.
【典题1】已知数列\(\{a_n\}\)中,\(a_1=1\),\(a_{n}=\dfrac{a_{n-1}}{5 a_{n-1}+2}(n \geq 2)\),求通项公式\(a_n\).
【解析】对\(a_{n}=\dfrac{a_{n-1}}{5 a_{n-1}+2}\)
两边取倒数,得\(\dfrac{1}{a_{n}}=\dfrac{5 a_{n-1}+2}{a_{n-1}}=2 \cdot \dfrac{1}{a_{n-1}}+5\)
令\(b_{n}=\dfrac{1}{a_{n}}\),则\(b_{n}=2 b_{n-1}+5\)
\(\therefore b_{n}+5=2\left(b_{n-1}+5\right)\)
\(∴\)数列\(\left\{b_{n}+5\right\}\)是首项为\(b_{1}+5=\dfrac{1}{a_{1}}+5=6\),公比为\(2\)的等比数列, \({\color{Red}{ (构造了等比数列)}}\)
\(\therefore b_{n}+5=6 \times 2^{n-1}=3 \times 2^{n} \Rightarrow b_{n}=3 \times 2^{n}-5\)
\(\therefore a_{n}=\dfrac{1}{b_{n}}=\dfrac{1}{3 \times 2^{n}-5}\).
【典题2】已知\(\{a_n\}\)中,\(a_1=1\),\(S_n\)是数列的前\(n\)项和,且\(S_{n+1}=\dfrac{S_{n}}{4 S_{n}+3}(n \geq 1)\),求\(a_n\).
【解析】递推式\(S_{n+1}=\dfrac{S_{n}}{4 S_{n}+3}\)
\({\color{Red}{ (可利用取倒数法求出数列S_n的通项S_n,再用a_n与S_n的关系式求a_n)}}\)
两边取倒数可变形为\(\dfrac{1}{S_{n+1}}=3 \cdot \dfrac{1}{S_{n}}+4\)(1)
则有\(\dfrac{1}{s_{n+1}}+2=3\left(\dfrac{1}{s_{n}}+2\right)\).
故数列\(\left\{\dfrac{1}{S_{n}}+2\right\}\)是以\(\dfrac{1}{S_{1}}+2=3\)为首项,\(3\)为公比的等比数列.
\(\therefore \dfrac{1}{S_{n}}+2=3 \cdot 3^{n-1}=3^{n}\),\(\therefore S_{n}=\dfrac{1}{3^{n}-2}\).
当\(n≥ 2\),\(a_{n}=S_{n}-S_{n-1}\)\(=\dfrac{1}{3^{n}-2}-\dfrac{1}{3^{n-1}-2}=\dfrac{-2 \cdot 3^{n}}{3^{2 n}-8 \cdot 3^{n}+12}\).
所以数列\(\{a_n\}\)的通项公式是\(a_{n}= \begin{cases}1, & (n=1) \\ \dfrac{-2 \cdot 3^{n}}{3^{2 n}-8 \cdot 3^{n}+12}, & (n \geq 2)\end{cases}\).
情况4
递推公式为\(a_{n+1}=p a_{n}+q^{n}\)(其中\(p\),\(q\)均为常数,\(pq(p-1)(q-1)≠0\)). (或\(a_{n+1}=p a_{n}+r q^{n}\),其中\(p\),\(q\),\(r\)均为常数) .
\({\color{Red}{方法一}}\) 在原递推公式两边同除以\(q^{n+1}\),得\(\dfrac{a_{n+1}}{q^{n+1}}=\dfrac{p}{q} \cdot \dfrac{a_{n}}{q^{n}}+\dfrac{1}{q}\),令\(b_{n}=\dfrac{a_{n}}{q^{n}}\),得\(b_{n+1}=\dfrac{p}{q} b_{n}+\dfrac{1}{q}\)再待定系数法解决;
\({\color{Red}{方法二}}\) 在原递推公式两边同除以\(p^{n+1}\),得\(\dfrac{a_{n+1}}{p^{n+1}}=\dfrac{a_{n}}{p^{n}}+\dfrac{1}{p} \cdot\left(\dfrac{q}{p}\right)^{n}\), 令\(b_{n}=\dfrac{a_{n}}{p^{n}}\),得\(b_{n+1}=b_{n}+\dfrac{1}{p} \cdot\left(\dfrac{q}{p}\right)^{n}\)再用累加法求解;
\({\color{Red}{方法三}}\) 待定系数法 设\(a_{n+1}+\lambda q^{n+1}=p\left(a_{n}+\lambda q^{n}\right)\),通过比较系数,求出\(λ\),构造出等比数列\(\left\{a_{n}+\lambda q^{n}\right\}\)再求解,此时要求\(p≠q\),否则该法失效.
【典题1】已知数列\(\{a_n\}\)满足\(a_{n+1}=2 a_{n}+4 \times 3^{n}\),\(a_1=9\),求数列\(\{a_n\}\)的通项公式.
【解析】\({\color{Red}{方法一\quad (两边同除以3^{n+1})}}\)
\(a_{n+1}=2 a_{n}+4 \times 3^{n}\)两边同除以\(3^{n+1}\),得\(\dfrac{a_{n+1}}{3^{n+1}}=\dfrac{2}{3} \cdot \dfrac{a_{n}}{3^{n}}+\dfrac{4}{3}\),
\({\color{Red}{(转化为递推公式为a_{n+1}=p a_{n}+q的情况)}}\)
令\(b_{n}=\dfrac{a_{n}}{3^{n}}\),则\(b_{n+1}=\dfrac{2}{3} b_{n}+\dfrac{4}{3}\),
\(\therefore b_{n+1}-4=\dfrac{2}{3}\left(b_{n}-4\right)\)
\(\therefore b_{n}-4=\left(b_{1}-4\right) \cdot\left(\dfrac{2}{3}\right)^{n-1}=-\left(\dfrac{2}{3}\right)^{n-1}\)\(\Rightarrow b_{n}=4-\left(\dfrac{2}{3}\right)^{n-1}\)
\(\therefore a_{n}=4 \cdot 3^{n}-3 \cdot 2^{n-1}\).
\({\color{Red}{方法二\quad (两边同除以2^{n+1}) }}\)
\(a_{n+1}=2 a_{n}+4 \times 3^{n}\)两边同除以\(2^{n+1}\),得\(\dfrac{a_{n+1}}{2^{n+1}}=\dfrac{a_{n}}{2^{n}}+2 \cdot\left(\dfrac{3}{2}\right)^{n}\),
\(\therefore b_{n}=\left(b_{n}-b_{n-1}\right)+\left(b_{n-1}-b_{n-2}\right)+\cdots\left(b_{2}-b_{1}\right)+b_{1}\) \({\color{Red}{(累加法)}}\)
\(=2 \cdot\left(\dfrac{3}{2}\right)^{n-1}+2 \cdot\left(\dfrac{3}{2}\right)^{n-2}+\cdots+2 \cdot\left(\dfrac{3}{2}\right)^{1}+\dfrac{9}{2}=6 \cdot\left(\dfrac{3}{2}\right)^{n-1}-\dfrac{3}{2}(n \geq 2)\)
\(\because b_{1}=\dfrac{9}{2}\)也满足上式
\(\therefore b_{n}=6 \cdot\left(\dfrac{3}{2}\right)^{n-1}-\dfrac{3}{2}(n \in N)\),
\(\therefore a_{n}=2^{n} \cdot b_{n}=4 \cdot 3^{n}-3 \cdot 2^{n-1}\).
\({\color{Red}{方法三\quad 待定系数法}}\)
设\(a_{n+1}+\lambda \cdot 3^{n+1}=2\left(a_{n}+\lambda \cdot 3^{n}\right)\),
化简得\(a_{n+1}=2 a_{n}-\lambda \cdot 3^{n}\),
与已知条件\(a_{n+1}=2 a_{n}+4 \times 3^{n}\)比较可知\(λ=-4\),
则\(a_{n+1}-4 \cdot 3^{n+1}=2\left(a_{n}-4 \cdot 3^{n}\right)\)
\(\therefore a_{n}-4 \cdot 3^{n}=\left(a_{1}-12\right) \cdot 2^{n-1}=-3 \cdot 2^{n-1}\),
\(\therefore a_{n}=4 \cdot 3^{n}-3 \cdot 2^{n-1}\).
【点拨】方法技巧主要都是体现在通过构造等差等比数列和把问题转化为前面“已知模型”去.
情况5
递推公式为\(a_{n+1}=p a_{n}^{r}\)型
\({\color{Red}{方法一\quad 对数变换法:}}\)该类型是等式两边取对数后转化为前边的类型,然后再用递推法或待定系法构造等比数列求出通项.
两边取对数得
\(\lg a_{n+1}=\lg \left(p a_{n}^{r}\right) \Rightarrow \lg a_{n+1}=\lg p+\operatorname{rlg} a_{n}\)
设\(b_{n}=\lg a_{n}\)
\(∴\)原等式变为\(b_{n+1}=r b_{n}+\lg p\)即变为基本型.
\({\color{Red}{方法二\quad 迭代法}}\),反复迭代使用\(a_{n+1}=p a_{n}^{r}\),一直推到\(a_1\),
\(a_{n}=p a_{n-1}^{r}=p\left(p a_{n-2}^{r}\right)^{r}=p^{r+1} a_{n-2}^{r^{2}}\)\(=p^{r+1}\left(p a_{n-3}^{r}\right)^{r^{2}}=p^{r^{2}+r+1} a_{n-3}^{r^{3}}=\cdots=f(r) a_{1}^{r^{n-1}}\).
【典题1】设正项数列\(\{a_n\}\)满足\(a_1=1\),\(a_{n}=3 a_{n-1}^{2}(n \geq 2)\), 求通项公式\(a_n\).
【解析】\({\color{Red}{方法一 \quad 对数变换法}}\)
\(a_{n}=3 a_{n-1}^{2}(n \geq 2)\)
将等式两边取对数得\(\log _{3} a_{n}=1+2 \log _{3} a_{n-1}\)\(\Rightarrow \log _{3} a_{n}+1=2\left(\log _{3} a_{n-1}+1\right)\)
\({\color{Red}{(为了计算简便取对数log_3x)}}\)
则\(\left\{\log _{3} a_{n}+1\right\}\)是以\(\log _{3} a_{1}+1=1\)为首项,公比为\(2\)等比数列,
\(\therefore \log _{3} a_{n}+1=2^{n-1}\),
\(\therefore a_{n}=3^{2^{n-1}-1}\).
\({\color{Red}{方法二 \quad 迭代法}}\)
由\(a_{n}=3 a_{n-1}^{2}(n \geq 2)\)可迭代得
\(a_{n}=3 a_{n-1}^{2}=3\left(3 a_{n-2}^{2}\right)^{2}=3 \cdot 3^{2} a_{n-2}^{2^{2}}\)\(=3 \cdot 3^{2}\left(3 a_{n-3}^{2}\right)^{2^{2}}=3 \cdot 3^{2} \cdot 3^{4} a_{n-3}^{2^{3}}=\cdots\)\(=3 \cdot 3^{2} \cdot 3^{4} \cdot 3^{2^{n-2}} a_{1}^{2^{n-1}}=3^{2^{n-1}-1}\)
\({\color{Red}{(在迭代的过程中,逐一保持“原始数值”,找到数值变化的规律,比如指数与下标的关系之类的) }}\)
巩固练习
1 (★★)数列\(\{a_n\}\)中,\(a_1=1\),\(a_{n+1}=\dfrac{2 a_{n}}{a_{n}+2}\left(n \in \boldsymbol{N}^{*}\right)\),则\(\dfrac{2}{101}\)是这个数列的第 \(\underline{\quad \quad}\) 项.
2 (★★)若数列\(\{a_n\}\)中,\(a_1=3\)且\(a_{n+1}=a_{n}^{2}\)(\(n\)是正整数),则它的通项公式是\(a_n=\)\(\underline{\quad \quad}\) .
3 (★★)已知数列\(\{a_n\}\)满足\(a_{1}=\dfrac{5}{2}\),\(a_{n}=3 a_{n-1}+1\)\(\left(n \geq 2, n \in \boldsymbol{N}^{*}\right)\).求数列\(\{a_n\}\)的通项公式.
4 (★★)已知数列\(\{a_n\}\)中,当\(n≥2\)时,\(a_{n}=\dfrac{a_{n-1}}{3 a_{n-1}+1}\),\(a_1=1\),求通项公式\(a_n\).
5 (★★)已知数列\(\{a_n\}\)满足\(a_{1}=\dfrac{7}{3}\),\(a_{n+1}=3 a_{n}-4 n+2\).求通项公式\(a_n\).
6 (★★)已知数列\(\{a_n\}\)中,\(a_{1}=\dfrac{5}{6}\),\(a_{n+1}=\dfrac{1}{3} a_{n}+\left(\dfrac{1}{2}\right)^{n+1}\),求\(a_n\).
7 (★★)数列\(\{a_n\}\)前\(n\)项和\(S_{n}=4-a_{n}-\dfrac{1}{2^{n-2}}\),求通项公式\(a_n\).
8 (★★★★)已知数列\(\{a_n\}\)的各项都是正数,且满足\(a_0=1\),\(a_{n+1}=\dfrac{1}{2} a_{n}\left(4-a_{n}\right)\),\(n∈N\).求数列\(\{a_n\}\)的通项公式\(a_n\).
参考答案
1.\(100\)
2.\(a_{n}=3^{2^{n-1}}\)
3.\(a_{n}=3^{n}-\dfrac{1}{2}\)
4.\(a_{n}=\dfrac{1}{3 n-2}\)
5.\(a_{n}=3^{n-2}+2 n\)
6.\(a_{n}=\dfrac{3}{2^{n}}-\dfrac{2}{3^{n}}\)
7.\(a_{n}=\dfrac{n}{2^{n-1}}\)
8.\(a_{n}=2-\left(\dfrac{1}{2}\right)^{2^{n}-1}\)
【方法六】分\(n\)奇偶讨论法
在有些数列问题中,有时要对\(n\)的奇偶性进行分类讨论以方便问题的处理.
\({\color{Red}{形如a_{n+1}+a_n=f(n)型 }}\)
(1)若\(a_{n+1}+a_{n}=d\)(\(d\)是常数),则数列\(\left\{a_{n}\right\}\)为“等和数列”,它是一个周期数列,周期为\(2\),其通项分奇数项和偶数项来讨论.
(2)若\(f(n)\)为\(n\)的函数(非常数)时,方法一是构造转化为\(a_{n+1}-a_{n}=f(n)\)型,再通过累加法来求出通项;方法二是用逐差法得\(a_{n+1}-a_{n-1}=f(n)-f(n-1)\),分奇数项和偶数项来讨论.
【典题1】数列\(\left\{a_{n}\right\}\)中,\(a_1=0\)且\(a_{n}+a_{n+1}=2 n\),求通项公式.
【解析】\({\color{Red}{ 方法一 构造转化为a_{n+1}-a_n=f(n)型}}\)
令\(b_{n}=(-1)^{n} a_{n}\)
则\(b_{n+1}-b_{n}=(-1)^{n+1} a_{n+1}-(-1)^{n} a_{n}=(-1)^{n+1}\left(a_{n+1}+a_{n}\right)=(-1)^{n+1} \cdot 2 n\)
\({\color{Red}{(成功把递推公式转化为a_{n+1}-a_{n}=f(n)型,接着用累加法) }}\)
\(∴n≥2\)时,得
\(\begin{aligned}
&b_{n}-b_{n-1}=(-1)^{n} \cdot 2(n-1) \\
&b_{n}-b_{n-2}=(-1)^{n-1} \cdot 2(n-2) \\
&\cdots \cdots \\
&b_{2}-b_{1}=(-1)^{2} \cdot 2
\end{aligned}\)
把以上\(n-1\)个等式累加得,
\(b_{n}=2\left[(-1)^{n} \cdot(n-1)+(-1)^{n-1} \cdot(n-2)+\cdots+(-1)^{2}\right]\)
\({\color{Red}{(出现(-1)^n可分n奇偶数讨论) }}\)
①当\(n\)是奇数时,
\(b_{n}=2\{[-(n-1)+(n-2)]+\cdots+[-2+1]\} \quad (*)\)
\(=2 \times[(-1)+\cdots+(-1)]=2 \cdot\left(-1 \times \dfrac{n-1}{2}\right)=1-n\),
\({\color{Red}{(注意到和式(*)中共有n-1项,当n是奇数,每相邻两个数之和为-1,共有\dfrac{n-1}{2}组) }}\)
此时\(b_n=-a_n\),则\(a_n=n-1\);
\(a_1=0\)也满足上式,故当\(n\)是奇数时,\(a_n=n-1\);
②当\(n\)是偶数时,由\(a_{n}+a_{n+1}=2 n\)得\(a_{n}=2 n-a_{n+1}=2 n-n=n\);
\({\color{Red}{ (求出n是奇数时a_n=n-1,再利用已知条件a_{n}+a_{n+1}=2 n求出n是偶数时的a_n,不对和式(*)讨论,这会简单些) }}\)
故a\(a_{n}=\left\{\begin{array}{l}
n-1, n \text { 为奇数 } \\
n, \quad n \text { 为偶数 }
\end{array}\right.\).
\({\color{Red}{方法二 逐差法 }}\)
\(\because a_{n}+a_{n+1}=2 n\)
\(∴n≥2\)时,\(a_{n-1}+a_{n}=2 n-2\)
两式相减得\(a_{n+1}-a_{n-1}=2\)
\(∴a_1 ,a_3 ,a_5\),…,构成以\(a_1=0\)为首项,\(2\)为公差的等差数列;
\(a_2 ,a_4 ,a_6\) ,…,构成以\(a_2=2\)为首项,\(2\)为公差的等差数列;
\(\therefore a_{2 k-1}=a_{1}+2(k-1)=2 k-2=(2 k-1)-1 \text {, }\),
\(a_{2 k}=a_{2}+2(k-1)=2 k\)
\({\color{Red}{ (对奇数项a_{2 k-1}和偶数项a_{2 k}用等差数列公式求出表达式)}}\)
故\(a_{n}= \begin{cases}n-1, & n \text { 为奇数 } \\ n, & n \text { 为偶数 }\end{cases}\).
\({\color{Red}{(最后还是要用n表达回a_n)}}\)
\({\color{Red}{形如a_n a_{n+1}=f(n)型 }}\)
(1) 若\(a_{n} a_{n+1}=d\)(\(d\)是常数),则数列\(\left\{a_{n}\right\}\)为“等积数列”,它是一个周期数列,周期为\(2\),其通项分奇数项和偶数项来讨论.
(2)若\(f(n)\)为\(n\)的函数(非常数)时,可用逐商法得\(\dfrac{a_{n+1}}{a_{n-1}}=\dfrac{f(n)}{f(n-1)}\),分奇数项和偶数项来讨论.
【典题1】已知数列\(\left\{a_{n}\right\}\)中,\(a_1=1\)且\(a_{n} a_{n+1}=2 \cdot\left(\dfrac{1}{4}\right)^{n}\),求通项公式.
【解析】由\(a_{n} a_{n+1}=2 \cdot\left(\dfrac{1}{4}\right)^{n}\)及\(a_{n+1} a_{n+2}=2 \cdot\left(\dfrac{1}{4}\right)^{n+1}\),
两式相除,得\(\dfrac{a_{n+2}}{a_{n}}=\dfrac{1}{4}\), \({\color{Red}{ (逐商法) }}\)
则\(a_1\),\(a_3\) ,… ,\(a_{2 n-1}\) ,…和\(a_2\),\(a_4\),… ,\(a_{2 n}\) ,…是公比为\(\dfrac{1}{4}\)的等比数列,
又\(a_1=1\) ,\(a_{2}=\dfrac{1}{2}\),
则\(a_{2 k-1}=a_{1} \cdot\left(\dfrac{1}{4}\right)^{k-1}=4^{1-k}\),即\(n\)为奇数时,\(a_{n}=2^{1-n}\);
\(a_{2 k}=a_{2} \cdot\left(\dfrac{1}{4}\right)^{k-1}=2^{1-2 k}\),即当\(n\)为偶数时,\(a_{n}=2^{1-n}\);
综合得\(a_{n}=2^{1-n}\).
巩固练习
1 (★★★) 已知数列\(\left\{a_{n}\right\}\)的前\(n\)项和\(S_n\)满足\(S_{n}-S_{n-2}=3 \cdot\left(-\dfrac{1}{2}\right)^{n-1}(n \geq 3)\),且\(S_1=1\),\(S_{2}=-\dfrac{3}{2}\),求数列\(\left\{a_{n}\right\}\)通项公式.
参考答案
- 【答案】\(a_{n}=\left\{\begin{array}{l}
4-3 \cdot\left(\dfrac{1}{2}\right)^{n-1}, n \text { 为奇数 } \\
-4+3 \cdot\left(\dfrac{1}{2}\right)^{n-1}, n \text { 为偶数 }
\end{array}\right.\).
【解析】依题意易求\(a_1=1\),\(a_{2}=-\dfrac{5}{2}\),\(a_{3}=\dfrac{13}{4}\)
\(\because S_{n}-S_{n-2}=3\left(-\dfrac{1}{2}\right)^{n-1}(n \geq 3)\)
\(\therefore a_{n}+a_{n-1}=3\left(-\dfrac{1}{2}\right)^{n-1}(n \geq 3)\)
当\(n≥4\)时,\(a_{n-1}+a_{n-2}=3\left(-\dfrac{1}{2}\right)^{n-2}\)
两式相减得\(a_{n}-a_{n-2}=9 \cdot\left(-\dfrac{1}{2}\right)^{n-1}\)
当\(n\)是偶数时,\(a_{n}=\left(a_{n}-a_{n-2}\right)+\left(a_{n}-a_{n-2}\right)+\cdots+\left(a_{4}-a_{2}\right)+a_{2}\)
\(=9 \cdot\left(-\dfrac{1}{2}\right)^{n-1}+9 \cdot\left(-\dfrac{1}{2}\right)^{n-3}+\cdots+9 \cdot\left(-\dfrac{1}{2}\right)^{3}-\dfrac{5}{2}\)
\(=9 \times \dfrac{-\dfrac{1}{8}\left[1-\left(\dfrac{1}{4}\right)^{\frac{n-2}{2}}\right]}{1-\dfrac{1}{4}}-\dfrac{5}{2}=-4+3 \cdot\left(\dfrac{1}{2}\right)^{n-1}(n \geq 4)\)
\(\because a_{2}=-\dfrac{5}{2}\)满足\(a_{n}=-4+3 \cdot\left(\dfrac{1}{2}\right)^{n-1}\)
\(\therefore a_{n}=-4+3 \cdot\left(\dfrac{1}{2}\right)^{n-1}\)(\(n\)是偶数)
当\(n\)是奇数时,由\(a_{n}+a_{n-1}=3\left(-\dfrac{1}{2}\right)^{n-1}(n \geq 3)\)
可得\(a_{n}=3\left(-\dfrac{1}{2}\right)^{n-1}-a_{n-1}\)\(=3\left(\dfrac{1}{2}\right)^{n-1}-\left[-4+3 \cdot\left(\dfrac{1}{2}\right)^{n-2}\right]=4-3\left(\dfrac{1}{2}\right)^{n-1}\)
\(∵a_1=1\)满足\(a_{n}=4-3\left(\dfrac{1}{2}\right)^{n-1}\)
\(\therefore a_{n}=-4+3 \cdot\left(\dfrac{1}{2}\right)^{n-1}\) (\(n\)是奇数)
\(\therefore a_{n}=\left\{\begin{array}{l} 4-3 \cdot\left(\dfrac{1}{2}\right)^{n-1}, n \text { 为奇数 } \\ -4+3 \cdot\left(\dfrac{1}{2}\right)^{n-1}, n \text { 为偶数 } \end{array}\right.\).
【方法七】数学归纳法
适用范围:数列前几项的数值出现一定规律或数值结构具有特点.
方法:由数列前几项用不完全归纳猜测出数列的通项公式,再利用数学归纳法证明其正确性.
【典题1】已知数列\(\left\{a_{n}\right\}\)满足\(a_{n+1}=a_{n}+\dfrac{8(n+1)}{(2 n+1)^{2}(2 n+3)^{2}}\),\(a_{1}=\dfrac{8}{9}\),求数列\(\left\{a_{n}\right\}\)的通项公式.
【解析】\({\color{Red}{ 方法一 \quad 累加法}}\)
\(\because a_{n+1}=a_{n}+\dfrac{8(n+1)}{(2 n+1)^{2}(2 n+3)^{2}}\),
\(\therefore a_{n+1}-a_{n}=\dfrac{1}{(2 n+1)^{2}}-\dfrac{1}{(2 n+3)^{2}}\),\({\color{Red}{ (要观察出式子可裂项) }}\)
则当\(n≥2\)时,\(a_{n}=\left(a_{n}-a_{n-1}\right)+\left(a_{n-1}-a_{n-2}\right)+\cdots+\left(a_{2}-a_{1}\right)+a_{1}\)
\(=\dfrac{1}{(2 n-1)^{2}}-\dfrac{1}{(2 n+1)^{2}}+\dfrac{1}{(2 n-3)^{2}}-\dfrac{1}{(2 n-1)^{2}}+\cdots+\dfrac{1}{3^{2}}-\dfrac{1}{5^{2}}+\dfrac{8}{9}\)
\(=\dfrac{1}{9}-\dfrac{1}{(2 n+1)^{2}}+\dfrac{8}{9}=1-\dfrac{1}{(2 n+1)^{2}}\).
验证当\(n=1\)时,上式成立.
\(\therefore a_{n}=1-\dfrac{1}{(2 n+1)^{2}}\).
\({\color{Red}{方法二 \quad 归纳法 }}\)
\(\because a_{1}=\dfrac{8}{9}=1-\dfrac{1}{9}\),\(a_{n+1}=a_{n}+\dfrac{8(n+1)}{(2 n+1)^{2}(2 n+3)^{2}}\)
\(\therefore a_{2}=\dfrac{24}{25}=1-\dfrac{1}{25}\),\(a_{3}=\dfrac{48}{49}=1-\dfrac{1}{49}\);
猜想\(a_{n}=1-\dfrac{1}{(2 n+1)^{2}}\),
\({\color{Red}{(通过递推公式算出前3项,根据数值特点(可看回观察法求a_n的技巧)猜想出通项公式a_n) }}\)
证明如下:①\(n=1\)时,结论成立;
②假设\(n=k\)时,结论成立,即\(a_{k}=1-\dfrac{1}{(2 k+1)^{2}}\),
则\(n=k+1\)时,
\(a_{k+1}=a_{k}+\dfrac{8(k+1)}{(2 k+1)^{2}(2 k+3)^{2}}\)\(=1-\dfrac{1}{(2 k+1)^{2}}+\dfrac{8(k+1)}{(2 k+1)^{2}(2 k+3)^{2}}=1-\dfrac{1}{(2 k+3)^{2}}\),
即\(n=k+1\)时,结论成立.
综上,\(a_{n}=1-\dfrac{1}{(2 n+1)^{2}}\).
【典题2】已知数列\(\left\{a_{n}\right\}\)的前\(n\)项和为\(S_n\),\(a_n>0\)且\(S_{n}=\dfrac{1}{2}\left(a_{n}+\dfrac{n}{a_{n}}\right)\), 求数列\(\left\{a_{n}\right\}\)通项公式.
【解析】\(\because S_{n}=\dfrac{1}{2}\left(a_{n}+\dfrac{n}{a_{n}}\right)\)
当\(n=1\)时,有\(S_{1}=\dfrac{1}{2}\left(a_{1}+\dfrac{1}{a_{1}}\right) \Rightarrow a_{1}^{2}=1 \Rightarrow a_{1}=1\),
当\(n=2\)时,
有\(S_{2}=\dfrac{1}{2}\left(a_{2}+\dfrac{2}{a_{2}}\right) \Rightarrow 1+a_{2}=\dfrac{1}{2}\left(a_{2}+\dfrac{2}{a_{2}}\right) \Rightarrow a_{2}^{2}+2 a_{2}=2\)\(\Rightarrow\left(a_{2}+1\right)^{2}=3 \Rightarrow a_{2}=\sqrt{3}-1\)
当n=3时,有\(S_{3}=\dfrac{1}{2}\left(a_{3}+\dfrac{3}{a_{3}}\right) \Rightarrow \sqrt{3}+a_{3}=\dfrac{1}{2}\left(a_{3}+\dfrac{3}{a_{3}}\right) \Rightarrow a_{3}^{2}+2 \sqrt{3} a_{3}=3\)
\(\Rightarrow\left(a_{3}+\sqrt{3}\right)^{2}=6 \Rightarrow a_{3}=\sqrt{6}-\sqrt{3}\)
\({\color{Red}{ (在计算的过程中也会发现一些规律,有助于猜想)}}\)
由\(a_{1}=1=\sqrt{1}-\sqrt{0}, a_{2}=\sqrt{3}-\sqrt{1}, a_{3}=\sqrt{6}-\sqrt{3}\)可猜想\(a_{n}=\sqrt{\dfrac{n(n+1)}{2}}-\sqrt{\dfrac{n(n-1)}{2}}\).
\({\color{Red}{ (通过观察法可得数列1,3,6…的通项是\dfrac{n(n+1)}{2},数列0,1,3…的通项是\dfrac{n(n-1)}{2})}}\)
以下利用数学归纳法证明,
①\(n=1\)时,结论显然成立;
②假设\(n=k\)时,结论成立,即\(a_{k}=\sqrt{\dfrac{k(k+1)}{2}}-\sqrt{\dfrac{k(k-1)}{2}}\),
则\(n=k+1\)时,有\(a_{k+1}=S_{k+1}-S_{k}=\dfrac{1}{2}\left(a_{k+1}+\dfrac{k+1}{a_{k+1}}\right)-\dfrac{1}{2}\left(a_{k}+\dfrac{k}{a_{k}}\right)\),
\(\therefore a_{k+1}=\dfrac{k+1}{a_{k+1}}-\left(a_{k}+\dfrac{k}{a_{k}}\right)=\dfrac{k+1}{a_{k+1}}-\sqrt{2 k(k+1)}\)
\(\therefore a_{k+1}^{2}+\sqrt{2 k(k+1)} a_{k+1}=k+1 \Rightarrow\left(a_{k+1}+\sqrt{\dfrac{k(k+1)}{2}}\right)^{2}=\dfrac{(k+2)(k+1)}{2}\)
\(\therefore a_{k+1}=\sqrt{\dfrac{(k+2)(k+1)}{2}}-\sqrt{\dfrac{k(k+1)}{2}}\) \({\color{Red}{ (其计算过程与算a_1,a_2 ,a_3时类似) }}\)
即\(n=k+1\)时,结论成立.
综上,\(a_{n}=\sqrt{\dfrac{n(n+1)}{2}}-\sqrt{\dfrac{n(n-1)}{2}}\).
巩固练习
1 (★★)设\(0<\theta<\dfrac{\pi}{2}\),已知\(a_{1}=2 \cos \theta\),\(a_{n+1}=\sqrt{2+a_{n}}\),猜想\(a_{n}=\)( )
A. \(2 \cos \dfrac{\theta}{2^{n}}\) \(\qquad \qquad \qquad\) B. \(2 \cos \dfrac{\theta}{2^{n-1}}\) \(\qquad \qquad \qquad\) C. \(2 \cos \dfrac{\theta}{2^{n+1}}\) \(\qquad \qquad \qquad\)D. \(2 \sin \dfrac{\theta}{2^{n}}\)
2 (★★)若数列\(\left\{a_{n}\right\}\)满足\(a_1=1\) ,\(a_{n+1}=2 a_{n}+3 \times 2^{n-1}\)计算\(a_2\),\(a_3\),\(a_4\)的值,由此归纳出\(a_n\)的公式,并证明你的结论.
3 (★★★)在各项均为正数的数列\(\left\{a_{n}\right\}\)中,\(S_n\)为数列\(\left\{a_{n}\right\}\)的前\(n\)项和,\(S_{n}=\dfrac{1}{2}\left(a_{n}+\dfrac{1}{a_{n}}\right)\),求其通项公式.
参考答案
- 【答案】\(B\)
【解析】由题意\(a_{n+1}=\sqrt{2+a_{n}}\),可得\(a_{2}=\sqrt{2+a_{1}}=\sqrt{2+2 \cos \theta}=2 \cos \dfrac{\theta}{2}\),
\(a_{3}=\sqrt{2+2 \cos \dfrac{\theta}{2}}=2 \cos \dfrac{\theta}{4}\),\(a_{4}=2 \cos \dfrac{\theta}{2^{3}}\),
猜想\(a_{n}=2 \cos \dfrac{\theta}{2^{n-1}}\),故选:\(B\). - 【答案】\(a_2=5\),\(a_3=16\),\(a_4=44\),\(a_{n}=(3 n-1) \cdot 2^{n-2}\)
【解析】\(\because a_{2}=2 a_{1}+3 \times 2^{\circ}=2 \times 1+3 \times 2^{\circ}\),
\(a_{3}=2\left(2 \times 1+3 \times 2^{\circ}\right)+3 \times 2^{1}=2^{2} \times 1+2 \times 3 \times 2^{1}\),
\(a_{4}=2\left(2^{2} \times 1+2 \times 3 \times 2^{1}\right)+3 \times 2^{2}=2^{3} \times 1+3 \times 3 \times 2^{2}\);
猜想\(a_{n}=2^{n-1}+(n-1) \times 3 \times 2^{n-2}=(3 n-1) \cdot 2^{n-2}\);
用数学归纳法证明:
1°当\(n=1\)时,\(a_{1}=2^{-1} \times 2=1\),结论正确;
2°假设\(n=k\)时,\(a_{k}=2^{k-2}(3 k-1)\)正确,
\(∴\)当\(n=k+1\)时,
\(a_{k+1}=2 a_{k}+3 \times 2^{k-1}=2 \times 2^{k-2}(3 k-1)+3 \times 2^{k-1}=2^{k-1}(3 k+2)\)
\(=2^{(k+1)-2}[(3(k+1)-1)]\)
结论正确;
由1°、2°知对\(n \in N^{*}\)有\(a_{n}=2^{n-2}(3 n-1)\) - 【答案】\(a_{n}=\sqrt{n}-\sqrt{n-1}\left(n \in N^{*}\right)\)
【解析】当\(n=1\)时,\(S_{1}=\dfrac{1}{2}\left(a_{1}+\dfrac{1}{a_{1}}\right)\),\(∵a_1=S_1\),\(a_n>0\),解得\(a_1=1\),
当\(n=2\)时,\(S_{2}=a_{1}+a_{2}=\dfrac{1}{2}\left(a_{2}+\dfrac{1}{a_{2}}\right)\),得\(a_2^2+2a_2-1=0\),\(\therefore a_{2}=\sqrt{2}-1\),
当\(n=3\)时,\(S_{3}=a_{1}+a_{2}+a_{3}=\dfrac{1}{2}\left(a_{3}+\dfrac{1}{a_{3}}\right)\),得\(a_{3}^{2}+2 \sqrt{2} a_{3}-1=0\),\(\therefore a_{3}=\sqrt{3}-\sqrt{2}\),
猜想\(a_{n}=\sqrt{n}-\sqrt{n-1}\),下面用数学归纳法证明,
当\(n=1\)时,\(a_{1}=1=\sqrt{1}-\sqrt{0}\),显然成立,
假设当\(n=k\)时,\(a_{k}=\sqrt{k}-\sqrt{k-1}\left(k \geq 1, k \in N^{*}\right)\),
当\(n=k+1\)时,
\(a_{k+1}=S_{k+1}-S_{k}=\dfrac{1}{2}\left(a_{k+1}+\dfrac{1}{a_{k+1}}\right)-\dfrac{1}{2}\left(a_{k}+\dfrac{1}{a_{k}}\right)\)\(=\dfrac{1}{2}\left(a_{k+1}+\dfrac{1}{a_{k+1}}\right)-\dfrac{1}{2}\left(\sqrt{k}-\sqrt{k-1}+\dfrac{1}{\sqrt{k}-\sqrt{k-1}}\right)\)
\(=\dfrac{1}{2}\left(a_{k+1}+\dfrac{1}{a_{k+1}}\right)-\sqrt{k}\)
\(\therefore a_{k+1}^{2}+2 \sqrt{k} a_{k+1}-1=0\),解得\(a_{k+1}=\sqrt{k+1}-\sqrt{k}\),
即当\(n=k+1\)时也满足\(a_{n}=\sqrt{n}-\sqrt{n-1}\),
综上可得\(a_{n}=\sqrt{n}-\sqrt{n-1}\left(n \in N^{*}\right)\).
【方法八】 不动点法(特征根法) (选学内容)
不动点的定义:函数\(f(x)\)的定义域为\(D\),若存在\(x_0∈D\),使得\(f(x_0 )=x_0\)成立,则称\(x_0\)为\(f(x)\)的不动点.
\({\color{Red}{形如a_{n+1}=\dfrac{A a_{n}+B}{C a_{n}+D}的数列 }}\)
对于数列\(a_{n+1}=\dfrac{A a_{n}+B}{C a_{n}+D}\),\(a_1=m\),\(n∈N^*\)(\(A、B、C、D\)是常数且\(C≠0\) ,\(AD-BC≠0\))
其特征方程为\(x=\dfrac{A x+B}{C x+D}\),变形为\(C x^{2}+(D-A) x-B=0\)
若有二异根\(α\) ,\(β\),则可令\(\dfrac{a_{n+1}-\alpha}{a_{n+1}-\beta}=c \cdot \dfrac{a_{n}-\alpha}{a_{n}-\beta}\)(其中\(c\)是待定常数),代入\(a_1\),\(a_2\)的值可求得\(c\)值.
这样数列\(\left\{\dfrac{a_{n}-\alpha}{a_{n}-\beta}\right\}\)是首项为\(\dfrac{a_{1}-\alpha}{a_{1}-\beta}\),公比为\(c\)的等比数列,于是这样可求得\(a_n\).
若有二重根\(α=β\),则可令\(\dfrac{1}{a_{n+1}-\alpha}=\dfrac{1}{a_{n}-\alpha}+c\)(其中\(c\)是待定常数),代入\(a_1\),\(a_2\)的值可求得\(c\)值.
这样数列\(\left\{\dfrac{1}{a_{n}-\alpha}\right\}\)是首项为\(\dfrac{1}{a_{1}-\alpha}\),公差为\(c\)的等差数列,于是这样可求得\(a_n\).
此方法又称不动点法.
【典题1】已知数列\(\left\{a_{n}\right\}\)满足\(a_1=2\) ,\(a_{n}=\dfrac{a_{n-1}+2}{2 a_{n-1}+1}(n \geq 2)\),求数列\(\left\{a_{n}\right\}\)的通项\(a_n\).
【解析】令\(x=\dfrac{x+2}{2 x+1}\),化简得\(2x^2-2=0\),解得\(x_1=1\) ,\(x_2=-1\),
令\(\dfrac{a_{n+1}-1}{a_{n+1}+1}=c\cdot \dfrac{a_{n}-1}{a_{n}+1}\)
由\(a_1=2\)得\(a_{2}=\dfrac{4}{5}\),可得\(c=-\dfrac{1}{3}\),
\(∴\)数列\(\left\{\dfrac{a_{n}-1}{a_{n}+1}\right\}\)是以\(\dfrac{a_{1}-1}{a_{1}+1}=\dfrac{1}{3}\)为首项,以\(-\dfrac{1}{3}\)为公比的等比数列,
\(\therefore \dfrac{a_{n}-1}{a_{n}+1}=\dfrac{1}{3} \cdot\left(-\dfrac{1}{3}\right)^{n-1}=(-1)^{n-1} \cdot\left(\dfrac{1}{3}\right)^{n}\),
\(\therefore a_{n}=\dfrac{3^{n}-(-1)^{n}}{3^{n}+(-1)^{n}}\).
【典题2】已知数列\(\left\{a_{n}\right\}\)满足\(a_1=2\) ,\(a_{n}=2-\dfrac{1}{a_{n-1}}(n \geq 2)\),求数列\(\left\{a_{n}\right\}\)的通项\(a_n\).
【解析】其特征方程为\(x=2-\dfrac{1}{x}\),解得\(x=1\),
\(\dfrac{1}{a_{n}-1}=\dfrac{1}{2-\dfrac{1}{a_{n-1}}-1}=\dfrac{1}{1-\dfrac{1}{a_{n-1}}}=\dfrac{a_{n-1}}{a_{n-1}-1}=1+\dfrac{1}{a_{n-1}-1}\),
\(∴\)数列\(\left\{\dfrac{1}{a_{n}-1}\right\}\)是以\(\dfrac{1}{a_{1}-1}=1\)为首项,公差为\(1\)的等差数列,
故\(\dfrac{1}{a_{n}-1}=n\),即\(a_{n}=\dfrac{n+1}{n}\).
\({\color{Red}{形如a_{n+2}=p a_{n+1}+q(p,q是常数)的数列 }}\)
当\(p≠0\)或\(1\),\(q≠0\)时,称\(x=px+q\)是数列\(\left\{a_{n}\right\}\)的一阶特征方程,其根\(x=\dfrac{q}{1-p}\)叫做特征根方程的特征根,这时数列\(\left\{a_{n}\right\}\)的通项公式为\(a_{n}=\left(a_{1}-\dfrac{q}{1-p}\right) p^{n-1}+\dfrac{q}{1-p}\).
【典题1】已知数列\(\left\{a_{n}\right\}\)中,\(a_1=1\),\(a_{n}=2 a_{n-1}+1(n \geq 2)\),求数列\(\left\{a_{n}\right\}\)的通项\(a_n\).
【解析】递推关系对应的递归函数为\(f(x)=2x+1\),由\(f(x)=x\)得不动点为\(-1\),
\(\therefore a_{n}-(-1)=2 a_{n-1}+1-(-1)\)
\(\therefore a_{n}+1=2\left(a_{n-1}+1\right)\)
\(\therefore a_{n}+1=\left(a_{1}+1\right) \cdot 2^{n-1}=2^{n}\)\(\therefore a_{n}=2^{n}-1\).
\({\color{Red}{形如a_{1}=m_{1}, a_{2}=m_{2}, a_{n+2}=p a_{n+1}+q a_{n}(p,q是常数)的数列}}\)
称\(x^2=px+q\)是数列\(\left\{a_{n}\right\}\)的二阶特征方程,其根\(x_1 ,x_2\)叫做特征方程的特征根.
若有二异根\(x_1 ,x_2\),则可令\(a_{n}=c_{1} x_{1}^{n}+c_{2} x_{2}^{n}\)(\(c_1\) ,\(c_2\)是待定常数)
若有二重根\(x_1=x_2\),则可令\(a_{n}=\left(c_{1}+n c_{2}\right) x_{1}^{n}\)(\(c_1\) ,\(c_2\)是待定常数)
再利用\(a_1=m_1\),\(a_2=m_2\)可求得\(c_1\),\(c_2\),进而求得\(a_n\).
【典题1】在数列\(\left\{a_{n}\right\}\)中,\(a_1=-1\),\(a_2=2\),\(a_{n+2}=5 a_{n+1}-6 a_{n}\left(n \in N^{*}\right)\),求通项公式\(a_n\).
\({\color{Red}{方法一 \quad 特征根法}}\)
【解析】的特征方程是\(x^2-5x+6=0\), 解得\(x_1=2 ,x_2=3\)
\(\therefore a_{n}=c_{1} 2^{n-1}+c_{2} 3^{n-1}\),
又由\(a_1=-1\),\(a_2=2\),得\(\left\{\begin{array}{l}
c_{1}+c_{2}=-1 \\
2 c_{1}+3 c_{2}=2
\end{array}\right.\),解得\(\left\{\begin{array}{c}
c_{1}=-5 \\
c_{2}=4
\end{array}\right.\),
故\(a_{n}=-5 \cdot 2^{n-1}+4 \cdot 3^{n-1}\).
\({\color{Red}{ 方法二 \quad 待定系数法}}\)
\(a_{n+2}=5 a_{n+1}-6 a_{n}\)式可化为:\(a_{n+2}+\lambda a_{n+1}=\eta\left(a_{n+1}+\lambda a_{n}\right)\)
即\(\left\{\begin{array}{c}
\eta-\lambda=5 \\
\eta \lambda=-6
\end{array}\right.\),解得\(\left\{\begin{array}{c}
\eta=2 \\
\lambda=-3
\end{array}\right.\)或\(\left\{\begin{array}{c}
\eta=3 \\
\lambda=-2
\end{array}\right.\),
不妨取\(λ=-2\),\(a_{n+2}=5 a_{n+1}-6 a_{n}\)式可化为:\(a_{n+2}-2 a_{n+1}=3\left(a_{n+1}-2 a_{n}\right)\)
则\(\left\{a_{n+1}-2 a_{n}\right\}\)是一个等比数列,首项\(a_2-2a_1=4\),公比为\(3\),
\(\therefore a_{n+1}=2 a_{n}+4 \cdot 3^{n-1}\),
两边同时除以\(3^{n}\)得\(\dfrac{a_{n+1}}{3^{n}}=\dfrac{2}{3} \cdot \dfrac{a_{n}}{3^{n-1}}+\dfrac{4}{3}\),
令\(b_{n}=\dfrac{a_{n}}{3^{n-1}}\) ,得\(b_{n+1}=\dfrac{2}{3} b_{n}+\dfrac{4}{3}\)_,_则\(b_{n+1}-4=\dfrac{2}{3}\left(b_{n}-4\right)\),
又\(b_1-4=a_1-4=-5\),\(\therefore b_{n}-4=-5 \cdot\left(\dfrac{2}{3}\right)^{n-1}\),
又\(b_{n}=\dfrac{a_{n}}{3^{n-1}}\) ,\(\therefore a_{n}=4 \cdot 3^{n-1}-5 \cdot 2^{n-1}\).
巩固练习
1 (★★) 设数列满足\(a_{1}=2\) ,\(a_{n+1}=\dfrac{5 a_{n}+4}{2 a_{n}+7}\),求数列\(\left\{a_{n}\right\}\)的通项\(a_n\).
2 (★★)已知数列\(\left\{a_{n}\right\}\)满足\(a_1=2\),\(a_{n+1}=\dfrac{2 a_{n}-1}{4 a_{n}+6}\left(n \in N^{*}\right)\) ,求数列\(\left\{a_{n}\right\}\)的通项\(a_n\).
3 (★★)已知数列\(\left\{a_{n}\right\}\)满足\(a_1=2\) ,\(a_2=3\), \(a_{n+2}=3a_{n+1}-2a_n (n∈N^*)\),求数列\(\left\{a_{n}\right\}\)的通项\(a_n\).
4 (★★)已知数列\(\left\{a_{n}\right\}\)满足\(a_1=1\) ,\(a_2=2\), \(4 a_{n+2}=4 a_{n+1}-a_n\left(n \in N^{*})\right.\),求数列\(\left\{a_{n}\right\}\)的通项\(a_n\).
5 (★★)求斐波拉契数列\(1,1,2,3,5,8,……\),的通项公式.
参考答案
- 【答案】\(a_{n}=\dfrac{4 \times 3^{n-1}+2}{4 \times 3^{n-1}-1}\)
【解析】对等式两端同时加参数\(t\),得
\(a_{n+1}+t=\dfrac{5 a_{n}+4}{2 a_{n}+7}+t=\dfrac{(2 t+5) a_{n}+7 t}{2 a_{n}+7}=(2 t+5) \dfrac{a_{n}+7 t+4}{2 a_{n}+7}\)
令\(t=\dfrac{7 t+4}{2 t+5}\),解得\(t=1\)或\(-2\),代入\(a_{n+1}+t=\dfrac{5 a_{n}+4}{2 a_{n}+7}+t\)得
\(a_{n+1}-1=3 \times \dfrac{a_{n}-1}{2 a_{n}+7}\),\(a_{n+1}+2=9 \times \dfrac{a_{n}+2}{2 a_{n}+7}\)
两式相除得\(\dfrac{a_{n+1}-1}{a_{n+1}+1}=\dfrac{1}{3} \times \dfrac{a_{n}-1}{a_{n}+2}\),即\(\left\{\dfrac{a_{n}-1}{a_{n}+2}\right\}\)是首项为\(\dfrac{a_{1}-1}{a_{1}+2}=\dfrac{1}{4}\),公比为\(\dfrac{1}{3}\)的等比数列,
\(\therefore \dfrac{a_{n}-1}{a_{n}+2}=\dfrac{1}{4} \times 3^{1-n}\),解得\(a_{n}=\dfrac{4 \times 3^{n-1}+2}{4 \times 3^{n-1}-1}\). - 【答案】\(a_{n}=\dfrac{13-5 n}{10 n-6}\)
【解析】令\(x=\dfrac{2 x-1}{4 x+6}\),即\(4x^2+4x+1=0\),解得\(x_{1}=x_{2}=-\dfrac{1}{2}\),
令\(\dfrac{1}{a_{n+1}+\dfrac{1}{2}}=\dfrac{1}{a_{n}+\dfrac{1}{2}}+c\)
由\(a_1=2\)得\(a_{2}=\dfrac{3}{14}\),求得\(c=1\),
\(∴\)数列\(\left\{\dfrac{1}{a_{n}+\frac{1}{2}}\right\}\)是以\(\dfrac{1}{a_{1}+\frac{1}{2}}=\dfrac{2}{5}\)为首项,以\(1\)为公差的等差数列,
\(\therefore \dfrac{1}{a_{n}+\frac{1}{2}}=\dfrac{2}{5}+n-1=n-\dfrac{3}{5}\) \(\therefore a_{n}=\dfrac{13-5 n}{10 n-6}\). - 【答案】\(a_{n}=1+2^{n-1}\)
【解析】其特征方程为\(x^2=3x-2\),解得\(x_1=1,x_2=2\),
令\(a_n=c_1 1^n+c_2 2^n=c_1+c_2 2^n\),
由\(a_{1}=2, a_{2}=3\)得\(\left\{\begin{array}{l} c_{1}+2 c_{2}=2 \\ c_{1}+4 c_{2}=3 \end{array}\right.\),解得\(\left\{\begin{array}{l} c_{1}=1 \\ C_{2}=\dfrac{1}{2} \end{array}\right.\), \(\therefore a_{n}=1+2^{n-1}\). - 【答案】\(a_{n}=\dfrac{3 n-2}{2^{n-1}}\)
【解析】其特征方程为\(4 x^{2}=4 x-1\),解得\(x_{1}=x_{2}=\dfrac{1}{2}\),
令\(a_{n}=\left(c_{1}+n c_{2}\right)\left(\dfrac{1}{2}\right)^{n}\)
由\(a_1=1,a_2=2\)得\(\left\{\begin{array}{c} \dfrac{1}{2}\left(c_{1}+c_{2}\right)=1 \\ \dfrac{1}{4}\left(c_{1}+2 c_{2}\right)=2 \end{array}\right.\),解得\(\left\{\begin{array}{c} c_{1}=-4 \\ c_{2}=6 \end{array}\right.\), \(\therefore a_{n}=\dfrac{3 n-2}{2^{n-1}}\) . - 【答案】\(a_{n}=\dfrac{1}{\sqrt{5}}\left[\left(\dfrac{1+\sqrt{5}}{2}\right)^{n}-\left(\dfrac{1-\sqrt{5}}{2}\right)^{n}\right]\)
【解析】令\(x^2=x+1\),解得\(x_{1}=\dfrac{1-\sqrt{5}}{2}, \quad x_{2}=\dfrac{1+\sqrt{5}}{2}\),
令\(a_{n}=c_{1}\left(\dfrac{1-\sqrt{5}}{2}\right)^{n}+c_{2}\left(\dfrac{1+\sqrt{5}}{2}\right)^{n}\),
由\(a_1=1,a_2=1\)得\(\left\{\begin{array}{c} \dfrac{1-\sqrt{5}}{2} c_{1}+\dfrac{1+\sqrt{5}}{2} c_{2}=1 \\ \left(\dfrac{1-\sqrt{5}}{2}\right)^{2} c_{1}+\left(\dfrac{1+\sqrt{5}}{2}\right)^{2} c_{2}=1 \end{array}\right.\),解得\(\left\{\begin{array}{l} c_{1}=-\dfrac{1}{\sqrt{5}} \\ c_{2}=\dfrac{1}{\sqrt{5}} \end{array}\right.\),
.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号