4.1 数列的概念与简单的表示
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【【高分突破系列】高二数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第二册同步提高,难度3颗星!
模块导图
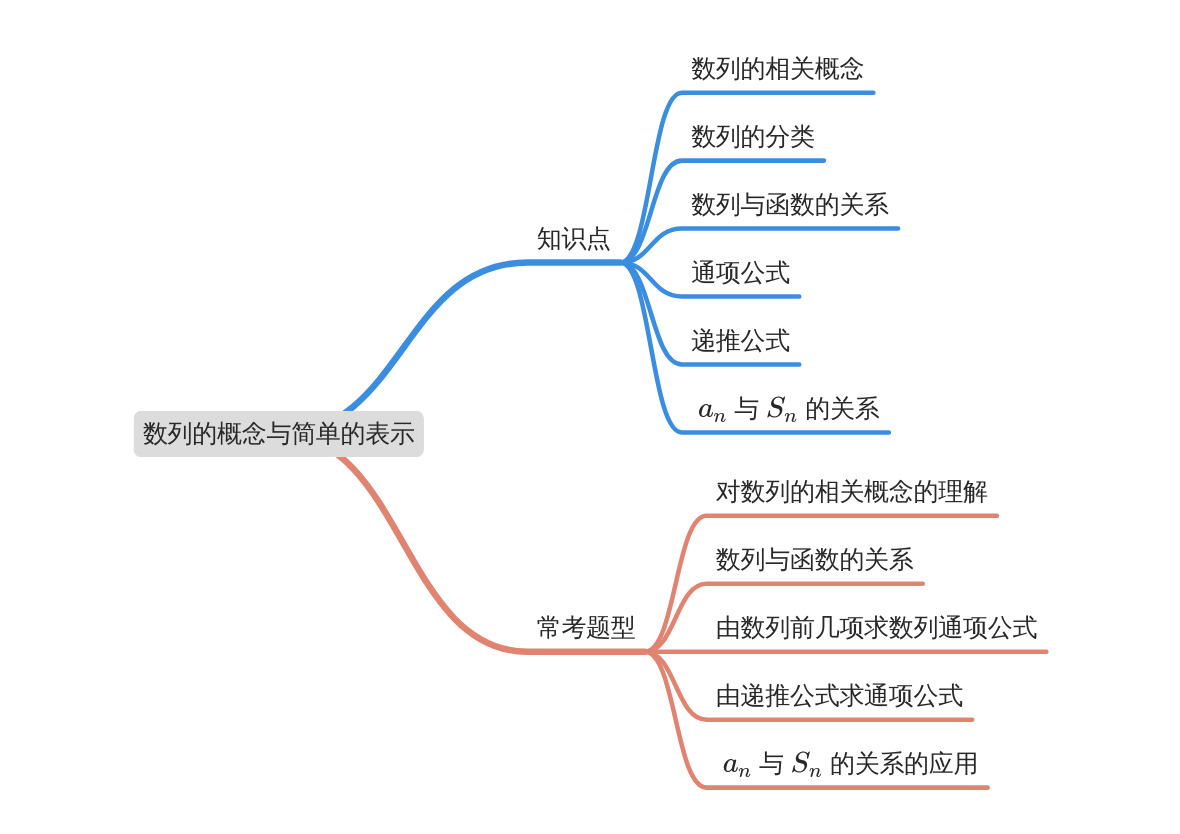
知识剖析
数列的相关概念
\((1)\)定义:数列是按照一定次序排列的一列数;
\((2)\)数列的项:数列中的每一个数叫做这个数列的项,第一项常称为首项;
\((3)\)数列的表示:数列的一般形式可以写成\(a_1\),\(a_2\),… ,\(a_n\),…,简记\(\{a_n\}\).
数列的分类
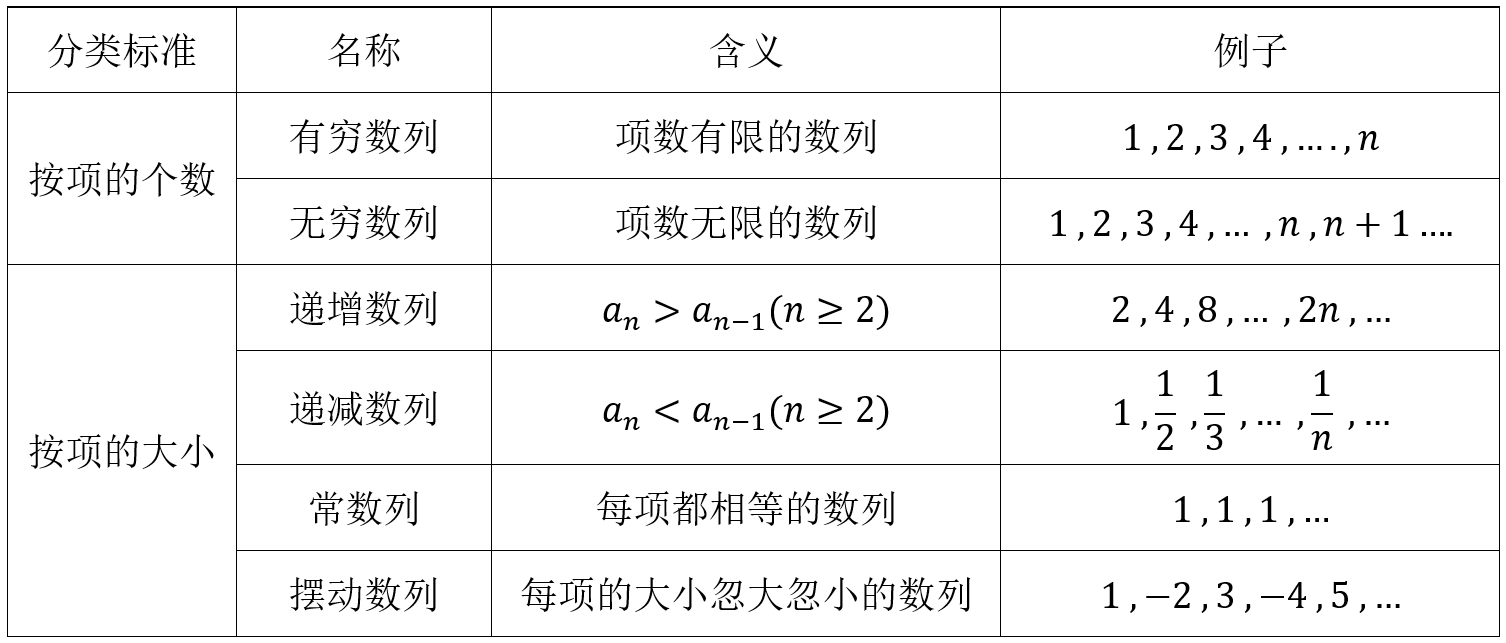
数列与函数的关系
数列就是定义在正整数集\(N^*\)(或它的有限子集\(\{1 ,2 ,3....n\}\))上的函数\(f(n)\),其图象是一系列有限或无限孤立的点.
\({\color{Red}{解释}}\)
日后研究数列的性质可以从函数的角度出发,比如单调性,最值等.
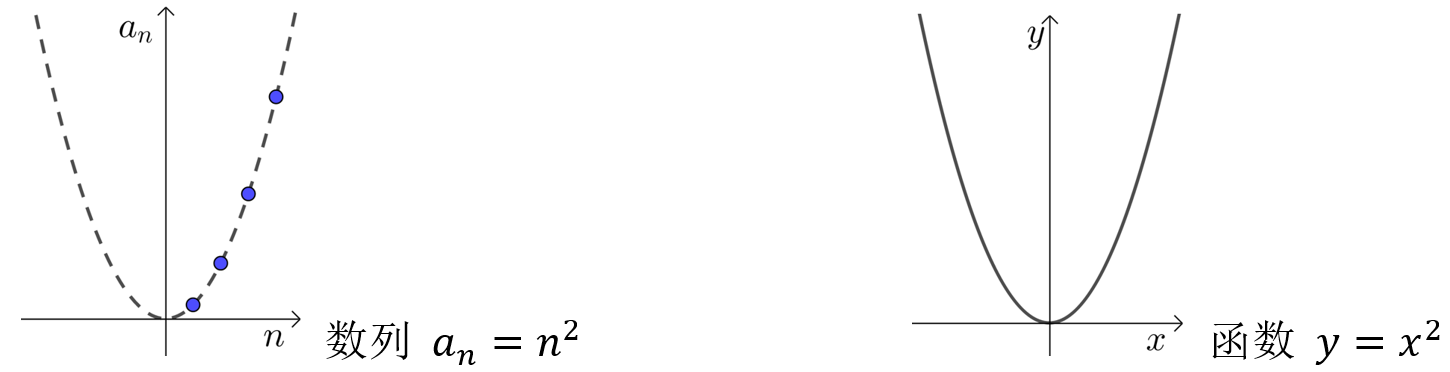
通项公式
如果数列\(\{a_n\}\)的第\(n\)项与序号\(n\)之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.
\({\color{Red}{Eg}}\) 数列\(1 ,0 ,1 ,0,…\),其通项公式可以是\(a_{n}=\dfrac{1+(-1)^{n+1}}{2}\),\(a_{n}=\sin ^{2} \dfrac{n \pi}{2}\)等.
\({\color{Red}{解释}}\)
\((1)a_n\)与\(\{a_n\}\)是不同的概念,\(\{a_n\}\)表示数列\(a_1\),\(a_2\),⋯,而\(a_n\)表示的是数列的第\(n\)项;
(2)数列的项与它的项数是不同的概念,数列的项是指这个数列中的某一个确定的数,它是一个函数值;而项数是指这个数在数列中的位置序号,它是自变量的值.
递推公式
若已知数列\(\{a_n\}\)的第一项\(a_1\)(或前\(n\)项),且任一项\(a_n\)和它的前一项\(a_{n-1}\)(或前\(n\)项)间的关系可以用一公式表示,那么这个公式叫做这个数列的递推公式.
\({\color{Red}{Eg}}\) \(a_1\)(初始条件),\(a_n=2a_{n-1}+3n\)(递推关系);
\(a_1=1\),\(a_2=2\)(初始条件) ,\(a_n=3a_{n-1}-2a_{n-2}\)(递推关系).
\(a_n\)与\(S_n\)的关系
若\(S_n\)为数列\(a_n\)的前\(n\)项和,即\(S_n=a_1+a_2+...+a_n\).
则\(a_{n}= \begin{cases}S_{1} & , n=1 \\ S_{n}-S_{n-1}, & n \geq 2\end{cases}\).
经典例题
【题型一】对数列的相关概念的理解
【典题1】下列有关数列的说法正确的是( )
①数列\(1 ,2 ,3\)可以表示成\(\{1 ,2 ,3\}\);
②数列\(-1 ,0 ,1\)与数列\(1 ,0 ,-1\)是同一数列;
③数列\(\left\{\dfrac{1}{n}\right\}\)的第\(k-1\)项是\(\dfrac{1}{k-1}\);
④数列中的每一项都与它的序号有关.
A.①② \(\qquad \qquad \qquad \qquad\) B.③④ \(\qquad \qquad \qquad \qquad\)C.①③ \(\qquad \qquad \qquad \qquad\) D.②④
【解析】对于①,\(\{1 ,2 ,3\}\)是集合,不是数列,故选项①错误;
对于②,数列是有序的,故数列\(-1 ,0 ,1\)与数列\(1 ,0 ,-1\)是不同的数列,故选项②错误;
对于③,数列\(\left\{\dfrac{1}{n}\right\}\)的第\(k-1\)项是\(\dfrac{1}{k-1}\),故选项③正确;
对于④,由数列的定义可知,数列中的每一项都与它的序号有关,故选项④正确.
故选:B.
【点拨】注意集合与数列的在“顺序、异同性、表示方法”上的区别. 数列是有序性,集合是无序性的;集合是互异性的,但数列不作要求.
【典题2】数列\(\{a_n\}\)为从\(a_0\)开始的非负整数有限数列,\(a_i\)表示在这个数列中\(i\)出现的次数.那么数列的项数不可能是 ( )
A.\(4\) \(\qquad \qquad \qquad \qquad\) B.\(5\) \(\qquad \qquad \qquad \qquad\) C.\(6\) \(\qquad \qquad \qquad \qquad\) D.\(7\)
【解析】\(a_i\)表示在这个数列中\(i\)出现的次数.\({\color{Red}{(理解这个是关键)}}\)
当\(a_0=2\),\(a_1=0\),\(a_2=2\),\(a_3=0\)时,满足条件,此时数列有\(4\)项,故排除\(A\);
当\(a_0=2\),\(a_1=1\),\(a_2=2\),\(a_3=0\),\(a_4=0\)时,满足条件,此时数列有\(5\)项,故排除\(B\);
当\(a_0=3\),\(a_1=2\),\(a_2=1\),\(a_3=1\),\(a_4 =0\),\(a_5=0\),\(a_6=0\)时,满足条件,此时数列有\(7\)项,故排除\(D\);
故选:\(C\).
【点拨】本题是选择题,优先考虑排除法,但留下了个问题:为什么项数不可能是\(6\)呢?还有其他项数不存在么?大家有什么想法,可以试试探究下!对问题的追问、深问是学数学的基本品质.
【典题3】求数列\(\left\{\dfrac{n}{n+2}\right\}\)是增减性.
【解析】 \({\color{Red}{方法一 \quad 作差法}}\)
\(a_{n+1}-a_{n}=\dfrac{n+1}{n+3}-\dfrac{n}{n+2}=\dfrac{2}{(n+3)(n+2)}>0\),
所以\(a_{n+1}>a_n\),故数列\(\left\{\dfrac{n}{n+2}\right\}\)是增数列.
\({\color{Red}{方法二 \quad 作商法}}\)
\(\dfrac{a_{n+1}}{a_{n}}=\dfrac{n+1}{n+3} \cdot \dfrac{n+2}{n}=\dfrac{n^{2}+3 n+2}{n^{2}+3 n}>1\),
又\(∵a_n>0\),所以\(a_{n+1}>a_n\),
故数列\(\left\{\dfrac{n}{n+2}\right\}\)是增数列.
\({\color{Red}{方法三 \quad 函数思想}}\)
\(a_{n}=\dfrac{n}{n+2}=\dfrac{1}{1+\dfrac{2}{n}}\),
\(\because f(x)=\dfrac{1}{1+\dfrac{2}{x}}\)在\((0 ,+∞)\)递增,
\(\therefore a_{n}=\dfrac{1}{1+\dfrac{2}{n}}\)也是随着\(n\)的增大而增大,
故数列\(\left\{\dfrac{n}{n+2}\right\}\)是增数列.
或\(a_{n}=\dfrac{n}{n+2}=1-\dfrac{2}{n+2}\),
由\(f(x)=1-\dfrac{2}{x+2}\)在\((0 ,+∞)\)递增也可得结论.
【点拨】求证数列单调性,常用方法有三:
① 作差法,比较\(a_{n+1}-a_{n}\)与\(0\)的大小;
② 作商法,比较\(\dfrac{a_{n+1}}{a_{n}}\)与\(1\)的大小,此时要注意\(a_n\)的正负;
③ 视通项公式为函数解析式,用函数单调性的方法处理,此时要注意\(n\)的取值范围是正整数.
【典题4】已知数列\(\{b_n\}\)满足\(b_{n}=2 \lambda\left(-\dfrac{1}{2}\right)^{n-1}-n^{2}\),若数列\(\{b_n\}\)是单调递减数列,则实数\(λ\)的取值范围是 \(\underline{\quad \quad}\) .
【解析】数列\(\{b_n\}\)是单调递减数列,
则\(b_{n+1}-b_{n}\)\(=2 \lambda\left(-\dfrac{1}{2}\right)^{n}-(n+1)^{2}-2 \lambda\left(-\dfrac{1}{2}\right)^{n-1}+n^{2}\)\(=6 \lambda\left(-\dfrac{1}{2}\right)^{n}-2 n-1<0\),
\({\color{Red}{(利用减数列的概念,相当于得到一个恒成立问题,可想到分类参数法求解,由于(-\dfrac{1}{2})^{n}的存在,}}\)
\({\color{Red}{需要对n的奇偶性进行分类讨论)}}\)
当\(n\)为偶数时,
\(6 \lambda<\dfrac{2 n+1}{\left(-\frac{1}{2}\right)^{n}}=(2 n+1)(-2)^{n}=(2 n+1) 2^{n}\)
由于\(\left\{(2 n+1) 2^{n}\right\}\)为递增数列,
则数列\(\left\{(2 n+1) 2^{n}\right\}\)的最小值\((2×2+1)\cdot 2^2=20\),
\(∴6λ<20\),即\(\lambda<\dfrac{10}{3}\),
当\(n\)为奇数时,
\(6 \lambda<\dfrac{2 n+1}{\left(-\frac{1}{2}\right)^{n}}=(2 n+1)(-2)^{n}=-(2 n+1) 2^{n}\)
由于\(\left\{-(2 n+1) 2^{n}\right\}\)为递减数列,
则数列\(\left\{-(2 n+1) 2^{n}\right\}\)的最大值\(-(2×1+1)\cdot 2=-6\),
\(∴6λ>-6\),\(∴λ>-1\),
综上所述实数\(λ\)的取值范围是\(\left(-1, \dfrac{10}{3}\right)\).
【点拨】本题充分考核了数列单调性的运用,其中也满满的“函数思想”,遇到类似\(\left(-\dfrac{1}{2}\right)^{n},(-1)^{n}\)式子进行奇偶性分类讨论是常用手段.
【典题5】若数列\(\left\{n(n+4)\left(\dfrac{2}{3}\right)^{n}\right\}\)中的最大项是第\(k\)项,求\(k\).
【解析】令\(a_{n}=n(n+4)\left(\dfrac{2}{3}\right)^{n}\),
假设\(\dfrac{a_{n+1}}{a_{n}}=\dfrac{(n+1)(n+5)\left(\dfrac{2}{3}\right)^{n+1}}{n(n+4)\left(\dfrac{2}{3}\right)^{n}}\)\(=\dfrac{2}{3} \dfrac{(n+1)(n+5)}{n(n+4)} \geq 1\),\({\color{Red}{(作商法)}}\)
则\(2(n+1)(n+5)≥3n(n+4)\),即\(n^2≤10\),
又\(n\)是整数,
即\(n≤3\)时,\(a_{n+1}>a_n\);当\(n≥4\)时,\(a_{n+1}<a_n\);
所以\(a_4\)最大.
【点拨】本题通过讨论数列\(\left\{n(n+4)\left(\dfrac{2}{3}\right)^{n}\right\}\)的增减性,从而得到最大值,其中就有函数思想的影子.
巩固练习
1(★)下列叙述正确的是( )
A.数列\(1 ,3 ,5 ,7\)与\(7 ,5 ,3 ,1\)是同一数列
B.数列\(0 ,1 ,2 ,3 ,…\)的通项公式是\(a_n=n\)
C.\(-1 ,1 ,-1 ,1 ,…\)是常数列
D.\(1 ,2 ,2^2 ,2^3 ,…\)是递增数列,也是无穷数列
2(★)对于项数都为\(m\)的数列\(\{a_n\}\)和\(\{b_n\}\),记\(b_k\)为\(a_1\),\(a_2\),… ,\(a_k\)\((k=1 ,2 ,… ,m)\)中的最小值,给出下列命题:
①若数列\(\{b_n\}\)的前\(5\)项依次为\(5 ,5 ,3 ,3 ,1\),则\(a_4=3\);
②若数列\(\{b_n\}\)是递减数列,则数列\(\{a_n\}\)也是递减数列;
③数列\(\{b_n\}\)可能是先递减后递增的数列;
④若数列\(\{a_n\}\)是递增数列,则数列\(\{b_n\}\)是常数列.
其中,是真命题的为( )
A.①④ \(\qquad \qquad \qquad \qquad\) B.①③ \(\qquad \qquad \qquad \qquad\) C.②③ \(\qquad \qquad \qquad \qquad\) D.②④
3(★)数列\(1 ,1 ,2 ,3 ,5 ,x ,13 ,…\)中的\(x\)等于( )
A.\(6\) \(\qquad \qquad \qquad \qquad\) B.\(7\) \(\qquad \qquad \qquad \qquad\) C.\(8\) \(\qquad \qquad \qquad \qquad\) D.\(11\)
4(★)【多选题】满足下列条件的数列\(\{a_n\}\)\((n∈N^*)\)是递增数列的为( )
A.\(a_{n}=\dfrac{1}{n}\) \(\qquad \qquad\) B.\(a_n=n^2+n\)\(\qquad \qquad\)C.\(a_n=1-2n\) \(\qquad \qquad\)D.\(a_n=2^n+1\)
5(★★)已知数列\(\{a_n\}\)是递增数列,且对于任意\(n∈N^*\),\(a_n=n^2+2λn+1\),则实数\(λ\)的取值范围是\(\underline{\quad \quad}\) .
6(★★)已知数列\(a_{n}=8+\dfrac{2 n-7}{2^{n}}\)若其最大项和最小项分别为\(M\)和\(m\),则\(m+M\)的值为\(\underline{\quad \quad}\).
7(★★)已知\(\{a_n\}\)满足\(a_{n}=(n-\lambda) 2^{n}\)\(\left(n \in \boldsymbol{N}^{*}\right)\),若\(\{a_n\}\)是递增数列,则实数\(λ\)的取值范围是\(\underline{\quad \quad}\).
8(★★★)在数列\(\{a_n\}\)中,已知\(a_{n}=\dfrac{a n}{b n+1}\),且\(a_{2}=\dfrac{6}{5}\),\(a_{3}=\dfrac{9}{7}\).
(1)求通项公式\(a_n\);
(2)求证:\(\{a_n\}\)是递增数列;
(3)求证:\(1 \leq a_{n}<\dfrac{3}{2}\).
参考答案
1.\(D\)
2.\(D\)
3.\(C\)
4.\(BD\)
5.\(\left(-\dfrac{3}{2},+\infty\right)\)
6.\(\dfrac{435}{32}\)
7.\((-∞ ,3)\)
8.\(\text { (1) } a_{n}=\dfrac{3 n}{2 n+1}\)
\((2)\)提示:作差法
\((3)\)提示:分离常数法
【题型二】数列与函数的关系
【典题1】数列\(\{a_n\}\)的通项\(a_n=-3n^2+2020n+1\),当\(a_n\)取最大值时,\(n=\)\(\underline{\quad \quad}\).
【解析】 \({\color{Red}{方法一 \quad 数列的单调性}}\)
根据题意,\(a_{n-1}=-3(n-1)^{2}+2020(n-1)+1\),
则\(a_n-a_{n-1}=-6n+2023\),
当\(1≤n≤336\)时,\(a_n-a_{n-1}>0\),即\(a_n>a_{n-1}\),
当\(n≥337\)时,\(a_n-a_{n-1}<0\),即\(a_n<a_{n-1}\),
而\(a_{337}>a_{336}\),
故数列\(\{a_n\}\)各项中最大项是第\(337\)项.
\({\color{Red}{方法二 \quad 函数法}}\)
依题意,\(a_n=-3n^2+2020n+1\),
表示抛物线\(f(n)=3n^2+2020n+1\)当\(n\)为正整数时对应的函数值,
又\(y=3x^2+2020x+1\)为开口向下的抛物线,
故到对称轴\(x=-\dfrac{2020}{2 \times(-3)}=\dfrac{1010}{3}\)距离越近的点,函数值越大,
故当\(n=337\)时,\(a_n=f(n)\)有最大值.
【点拨】数列是特殊的函数,可用数形结合的方法,但要注意自变量\(n\)是正整数.
【典题2】数列\(\{a_n\}\)的通项\(a_{n}=\dfrac{n}{n^{2}+90}\),则数列\(\{a_n\}\)中的最大值是\(\underline{\quad \quad}\).
【解析】\(a_{n}=\dfrac{n}{n^{2}+90}=\dfrac{1}{n+\dfrac{90}{n}}\),
\(\because f(x)=x+\dfrac{90}{x}\)在\((0,3 \sqrt{10})\)上单调递减,在\((3 \sqrt{10},+\infty)\)上单调递增,\({\color{Red}{(对勾函数)}}\)
\({\color{Red}{(9<3 \sqrt{10}<10,由于n只能取正整数,故还要比较f(9)、f(10)大小)}}\)
\(\therefore f(9)=9+10=19\),\(f(10)=9+10=19\)
即\(f(9)=f(10)\)为最小值,
此时\(a_{n}=\dfrac{n}{n^{2}+90}\)取得最大值为\(a_{9}=a_{10}=\dfrac{1}{19}\).
【点拨】根据数列的通项公式想到与之对应的函数,形如\(y=\dfrac{\text { 一次函数 }}{\text { 二次函数 }}\)的函数和对勾函数与基本不等式有关.
【典题3】【多选题】对于数列\(\{a_n\}\),定义\(b_{n}=a_{n}-\dfrac{1}{a_{n}}\)\(\left(n \in N^{*}\right)\),称数列\(\{b_n\}\)是\(\{a_n\}\)的“倒差数列”.下列叙述正确的有( )
A.若数列\(\{a_n\}\)单调递增,则数列\(\{b_n\}\)单调递增
B.若数列\(\{b_n\}\)是常数列,数列\(\{a_n\}\)不是常数列,则数列\(\{a_n\}\)是周期数列
C.若\(a_{n}=1-\left(-\dfrac{1}{2}\right)^{n}\),则数列\(\{b_n\}\)没有最小值
D.若\(a_{n}=1-\left(-\dfrac{1}{2}\right)^{n}\),则数列\(\{b_n\}\)有最大值
【解析】对于\(A\):函数\(f(x)=x-\dfrac{1}{x}\)在\((-∞ ,0)\)和\((0 ,+∞)\)上单调递增,但在整个定义域上不是单调递增,可知数列\(\{a_n\}\)单调递增时数列\(\{b_n\}\)不一定是单调递增,
\({\color{Red}{(利用复合函数的单调性思考,要a_n>0或a_n<0才成立;举个反例易排除A)}}\)
如:\(a_{n}=n-\dfrac{5}{2}\),则\(b_{2}=-\dfrac{1}{2}+2=\dfrac{3}{2}\),\(b_{3}=\dfrac{1}{2}-2=-\dfrac{3}{2}\),故\(A\)错误;
对于\(B\):数列\(\{b_n\}\)是常数列,
\(\therefore a_{n+1}-\dfrac{1}{a_{n+1}}=a_{n}-\dfrac{1}{a_{n}}\)\(\Rightarrow\left(a_{n+1}-a_{n}\right)\left(1+\dfrac{1}{a_{n} a_{n+1}}\right)=0\),
\(∵\)数列\(\{a_n\}\)不是常数列,\(∴a_{n+1}-a_n≠0\),
\(\therefore 1+\dfrac{1}{a_{n} a_{n+1}}=0\),整理可得\(a_{n+1}=-\dfrac{1}{a_{n}}\),\(\therefore a_{n+2}=-\dfrac{1}{a_{n+1}}=a_{n}\),
\({\color{Red}{(类比:若f(x)满足f(x+1)=-f(x),则f(x)是以2为周期的函数)}}\)
\(∴\)数列\(\{a_n\}\)是以\(2\)为周期的周期数列,故\(B\)正确;
对于\(CD\),若\(a_{n}=1-\left(-\dfrac{1}{2}\right)^{n}\),
则\(b_{n}=1-\left(-\dfrac{1}{2}\right)^{n}-\dfrac{1}{1-\left(-\dfrac{1}{2}\right)^{n}}\)
\({\color{Red}{(遇到(-\dfrac{1}{2})^{n}进行奇偶性分类讨论)}}\)
①当\(n\)为偶数时,
\(b_{n}=1-\dfrac{1}{2^{n}}-\dfrac{1}{1-\dfrac{1}{2^{n}}}=1-\dfrac{1}{2^{n}}-\dfrac{2^{n}}{2^{n}-1}\)\(=-1-\dfrac{1}{2^{n}}-\left(1+\dfrac{1}{2^{n}-1}\right)=-\left(\dfrac{1}{2^{n}}+\dfrac{1}{2^{n}-1}\right)\)
易得\(b_n<0\)且\(\{b_n\}\)偶数项单调递增,
此时\(\left(b_{n}\right)_{\min }=b_{2}=-\left(\dfrac{1}{4}+\dfrac{1}{3}\right)=-\dfrac{7}{12}\),
②当\(n\)为奇数时,
\(b_{n}=1+\dfrac{1}{2^{n}}-\dfrac{1}{1+\dfrac{1}{2^{n}}}=1+\dfrac{1}{2^{n}}-\dfrac{2^{n}}{2^{n}+1}\)\(=1+\dfrac{1}{2^{n}}-\left(1-\dfrac{1}{2^{n}+1}\right)=\dfrac{1}{2^{n}+1}+\dfrac{1}{2^{n}}\)
易得\(b_n>0\)且\(\{b_n\}\)奇数项单调递减,
此时\(\left(b_{n}\right)_{\max }=b_{1}=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}\),
由以上分析可得,数列\(\{b_n\}\)的图象如图,

\({\color{Red}{(数形结合的威力还是很大的,突出前面确定b_n>0(n为奇数),b_n<0(n为偶数)的必要性)}}\)
故数列\(\{b_n\}\)有最大值和最小值,即\(C\)错误,\(D\)正确,
故本题选\(BD\).
【点拨】本题可进一步理解数列作为一特别函数,看到两者的共同点,在讨论其性质均可利用到函数的周期性、复合函数单调性、最值等众多性质,最主要是通过数列通项公式的形式你可以想到与之对应的函数不,本题实际可以理解为复合函数.
巩固练习
1(★★)在数列\(\{a_n\}\)中,\(a_n=-2n^2+29n+3\),则此数列最大项的值是\(\underline{\quad \quad}\).
2(★★)数列\(\{a_n\}\)中,\(a_{n}=\dfrac{n-\sqrt{2006}}{n-\sqrt{2007}}\),则该数列前\(100\)项中的最大项与最小项分别是\(\underline{\quad \quad}\).
3(★★)若数列\(\{a_n\}\)的通项公式为\(a_{n}=\dfrac{n}{n^{2}+2020}\)\(\left(n \in N^{*}\right)\),则这个数列中的最大项\(\underline{\quad \quad}\).
4(★★★)数列\(\{a_n\}\)的通项公式为\(a_{n}=\left(\dfrac{4}{5}\right)^{2 n-4}-\left(\dfrac{4}{5}\right)^{n-2}\),则数列\(\{a_n\}\)( )
A.有最大项,无最小项\(\qquad \qquad\) B.有最小项,无最大项 \(\qquad \qquad\)C.既有最大项又有最小项 \(\qquad \qquad\) D.既无最大项又无最小项
5(★★)数列\(\{a_n\}\)中,\(a_{n}=2 n+\dfrac{k}{n}\),若对任意\(n∈N^*\),都有\(a_n≥a_3\)成立,则实数\(k\)的取值范围为( )
A.\([12 ,24]\) \(\qquad \qquad \qquad \qquad\) B.\((12 ,24]\) \(\qquad \qquad \qquad \qquad\)C.\([3 ,12]\) \(\qquad \qquad \qquad \qquad\) D.\((3 ,12]\)
6(★★★) 已知\(\{x_n\}\)是递增数列,且\(x_n≥0\),则关于数列\(\{x_n\}\),对任意的正整数\(p ,q\),下列结论不可能成立的( )
A.\(x_{pq}=px_q+qx_p\) \(\qquad \qquad\)B.\(x_{p+q}=px_q+qx_p\) \(\qquad \qquad\) C.\(x_{pq}=x_p+x_q-1\)\(\qquad \qquad\) D.\(x_{p+q}=2x_p x_q\)
7(★★)数列\(\{a_n\}\)中,\(a_{n}=n-\sqrt{n^{2}+2}\),求数列\(\{a_n\}\)的最大项和最小项.
参考答案
1.\(1108\)
2.\(a_{45},a_{44}\)
3.第\(44\)项
4.\(C\)
5.\(A\)
6.\(B\)
7.数列\(\{a_n\}\)的最小项为\(a_{1}=1-\sqrt{3}\),没有最大项.
【题型三】由数列前几项求数列通项公式
【典题1】写出下列数列\(\{a_n\}\)的一个通项公式:
\((1)-7 ,14 ,-21 ,28,…\);
\((2)\dfrac{1}{4}, \dfrac{3}{8}, \dfrac{5}{16}, \dfrac{7}{32} \ldots\);
\((3)2 ,5 ,10 ,17 ,26 ,…\);
\((4)2 ,32 ,332 ,3332 ,33332 ,….\);
\((5)1 ,2 ,2 ,3 ,3 ,4 ,4 ,….\)
【解析】\({\color{Red}{分解结构法}}\)
\((1)\)数列\(-7 ,14 ,-21 ,28\),…每项可分解成符号和项的绝对值相乘得到,
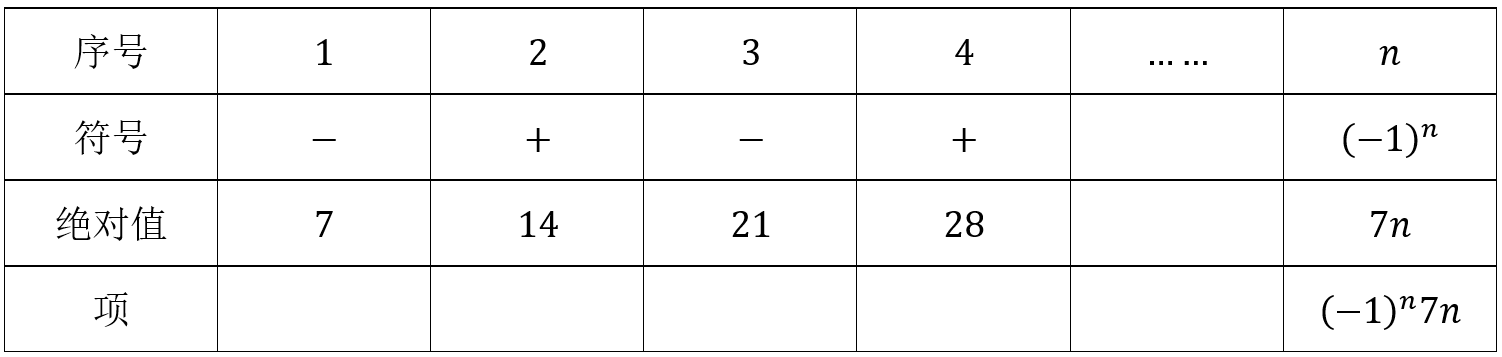
故\(a_{n}=(-1)^{n} 7 n\);
\({\color{Red}{(奇偶性的符号变换规律可考虑(-1)^{n}或(-1)^{n-1})}}\)
\((2)\)数列\(\dfrac{1}{4}, \dfrac{3}{8}, \dfrac{5}{16}, \dfrac{7}{32} \ldots\)每项可分解成分子和分母相除得到,
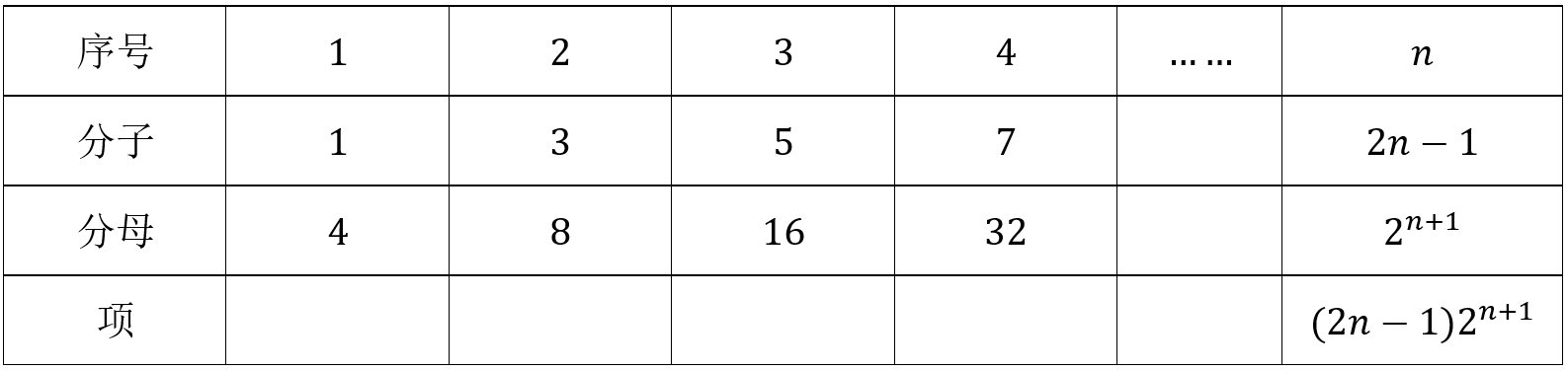
\({\color{Red}{ (分子相邻数之间的差是2,是等差数列;分母相邻数之间是2倍的关系,是等比数列)}}\)
故\(a_n=(2n-1)2^{n+1}\)
\({\color{Red}{变形法}}\)
\((3)\)数列\(2 ,5 ,10 ,17 ,26 ,…\)中若每项减去\(1\),则变成\(1 ,4 ,9 ,16 ,25 ,…\),
这些数都是完全平方数,易想到数列的通项是\(n^2\),
则原数列只需要在这基础上加回\(1\)便可,即\(a_n=n^2+1\).
\((4)\)数列\(2 ,32 ,332 ,3332 ,33332 ,….\)中若每项加上\(1\),
则变成\(3 ,33 ,333 ,3333 ,33333 ,….\),
再每项乘以\(3\),变成\(9 ,99 ,999 ,9999 ,99999 ,…\)
其中\(9=10-1\),\(99=10^2-1\),\(999=10^3-1\),\(9999=10^4-1\),\(99999=10^5-1\),
则其通项\(b_n=10^{n+1}-1\),
要求原数列的通项公式,
则“逆回去”,除以\(3\)再减\(1\)可得\(a_{n}=\dfrac{b_{n}}{3}-1=\dfrac{10^{n+1}-1}{3}-1=\dfrac{10^{n+1}-4}{3}\)
\({\color{Red}{奇偶项拆分}}\)
\((5)\)数列\(1 ,2 ,2 ,3 ,3 ,4 ,4 ,…\), 相邻每项之间没什么关系,若分奇偶性来看,就简单多了,
可得奇数项为\(1 ,2 ,3 ,4 ,…\), 可得\(a_{n}=\dfrac{n+1}{2}\).
偶数项为\(2 ,3 ,4 ,…\), 可得\(a_{n}=\dfrac{n+2}{2}\).
则该数列通项公式\(a_{n}=\left\{\begin{array}{l}
\dfrac{n+1}{2}, n \text { 为奇数 } \\
\dfrac{n+2}{2}, n \text { 为偶数 }
\end{array}\right.\).
巩固练习
1(★)数列\(\sqrt{2}\),\(\sqrt{5}\),\(2 \sqrt{2}\),\(\sqrt{11}\),⋅⋅⋅的一个通项公式为( )
A.\(\sqrt{3 n-3}\) \(\qquad \qquad \qquad \qquad\) B.\(\sqrt{3 n-1}\) \(\qquad \qquad \qquad \qquad\) C.\(\sqrt{3 n+1}\) \(\qquad \qquad \qquad \qquad\) D.\(\sqrt{3 n+3}\)
2(★)数列\(1\),\(-\dfrac{\sqrt{2}}{2}\),\(\dfrac{1}{2}\),\(-\dfrac{\sqrt{2}}{4}\),\(\dfrac{1}{4}\)…的一个通项公式为( )
A.\(\left(-\dfrac{1}{2}\right)^{n-1}\) \(\qquad \qquad\) B.\(\left(-\dfrac{\sqrt{2}}{2}\right)^{n}\) \(\qquad \qquad\) C.\((-1)^{n}\left(\dfrac{\sqrt{2}}{2}\right)^{n-1}\) \(\qquad \qquad\) D.\((-1)^{n+1}\left(\dfrac{\sqrt{2}}{2}\right)^{n-1}\)
3(★)【多选题】已知数列\(0\),\(2\),\(0\),\(2\),\(0\),\(2\),…,则前六项适合的通项公式为( )
A.\(a_n=1+(-1)^n\)
B.\(a_{n}=2 \cos \dfrac{n \pi}{2}\)
C.\(a_{n}=2\left|\sin \dfrac{(n+1) \pi}{2}\right|\)
D.\(a_{n}=1-\cos (n-1) \pi+(n-1)(n-2)\)
4(★★★)写出下列数列的一个通项公式:
\(\text { (1) } \dfrac{1}{2}, 2, \dfrac{9}{2}, 8, \dfrac{25}{2}, \ldots\);
\((2)1 ,-3 ,5 ,-7 ,9…\);
\((3)1 ,2 ,1 ,2 ,1 ,2…\);
\(\text { (4) } \dfrac{4}{5}, \dfrac{9}{10}, \dfrac{16}{17}, \dfrac{25}{26}, \ldots\);
\((5)7 ,77 ,777 ,7777 ,…\);
\((6)1 ,3 ,6 ,10 ,15 ,…\);
参考答案
1.\(B\)
2.\(D\)
3.\(AC\)
4.\(\text { (1) } a_{n}=\dfrac{n^{2}}{2}\);
\(\text { (2) } a_{n}=(-1)^{n+1} \times(2 n-1)\);
\(\text { (3) } a_{n}=\dfrac{3}{2}+(-1)^{n}\left(\dfrac{1}{2}\right)\);
\(\text { (4) } a_{n}=\dfrac{n^{2}}{n^{2}+1}\);
\(\text { (5) } a_{n}=\dfrac{7}{9}\left(10^{n}-1\right)\);
\(\text { (6) } a_{n}=\dfrac{n(n+1)}{2}\).
【题型四】由递推公式求通项公式
【典题1】已知数列\(\{a_n\}\)满足\(a_1=2\),\(a_{n+1}=a_{n}+\ln \left(1+\dfrac{1}{n}\right)\),求\(a_n\).
【解析】由条件知\(a_{n+1}-a_{n}=\ln \left(1+\dfrac{1}{n}\right)=\ln \dfrac{n+1}{n}=\ln (n+1)-\ln n\)
\(\therefore a_{2}-a_{1}=\ln 2-\ln 1\),\(a_{3}-a_{2}=\ln 3-\ln 2\),\(a_{4}-a_{3}=\ln 4-\ln 3\ldots\)
\(a_{n-1}-a_{n-2}=\ln (n-1)-\ln (n-2)\),\(a_{n}-a_{n-1}=\ln n-\ln (n-1)\)
把以上\(n-1\)个式子累加得到
\(\begin{aligned}
&a_{n}-a_{1} \\
&=\ln 2-\ln 1+\ln 3-\ln 2+\ln 4-\ln 3+\cdots \\
&\quad+\ln (n-1)-\ln (n-2)+\ln n-\ln (n-1) \\
&=\ln n-\ln 1 \\
&=\ln n(n \geq 2)
\end{aligned}\)
\(∴a_n=a_1+\ln n=\ln n+2 (n≥2)\)
\(∵a_1=2\)满足上式,
故\(a_n=\ln n+2 (n∈N^*)\)
【点拨】这是累加法,适合形如\(a_{n+1}=a_n+f(n)\)的递推公式求解通项公式.
【典题2】已知\(a_1=1\),\(a_{n}=n\left(a_{n+1}-a_{n}\right)\)\(\left(n \in N^{*}\right)\),求数列\(\{a_n\}\)通项公式.
【解析】\(\because a_{n}=n\left(a_{n+1}-a_{n}\right)\),
\(\therefore \dfrac{a_{n+1}}{a_{n}}=\dfrac{n+1}{n}\),
又有\(a_{n}=a_{1} \cdot \dfrac{a_{2}}{a_{1}} \cdot \dfrac{a_{3}}{a_{2}} \ldots \dfrac{a_{n}}{a_{n-1}}\)\(=1 \times \dfrac{2}{1} \times \dfrac{3}{2} \times \ldots \times \dfrac{n}{n-1}=n(n \geq 2)\),
\(∵a_1=1\)满足上式,
\(∴ a_n=n (n∈N^*)\).
【点拨】这是累加法,适合形如\(a_{n+1}=f(n)\cdot a_n\)的递推公式求解通项公式.
巩固练习
1(★★)在数列\(\{a_n\}\)中,已知\(a_1=1\),\(a_2=5\),且\(a_{n+2}=a_{n+1}-a_{n}\)\(\left(n \in N^{*}\right)\),则\(a_{2020}=\)\(\underline{\quad \quad}\).
2(★★)已知数列\(\{a_n\}\)满足\(a_{1}=\dfrac{1}{2}\),\(a_{n+1}=a_{n}+\dfrac{1}{n^{2}+n}\),求\(a_n\).
3(★★)已知\(a_1=3\),\(a_{n+1}=\dfrac{3 n-1}{3 n+2} a_{n}(n \geq 1)\),求\(a_n\).
4(★★)设数列\(\{a_n\}\)是首项为\(1\)的正项数列,且\((n+1) a_{n+1}^{2}-n a_{n}^{2}+a_{n+1} a_{n}=0\), 求通项公式是\(a_n\).
参考答案
1.\(-1\)
2.\(a_{n}=\dfrac{3}{2}-\dfrac{1}{n}\)
3.\(a_{n}=\dfrac{6}{3 n-1}\)
4.\(a_{n}=\dfrac{1}{n}\)
【题型五】a_n与S_n的关系的应用
【典题1】已知数列\(\{a_n\}\)的前\(n\)项和\(S_n\),满足关系\(\lg(S_n+2)=n\),求\(\{a_n\}\)的通项公式.
【解析】\(∵\lg(S_n+2)=n\),\(∴S_n=10^n-2\)
当\(n≥2\)时,\(a_{n}=S_{n}-S_{n-1}=9 \times 10^{n-1}\)
当\(n=1\)时,\(a_1=S_1=8\)不满足\(a_{n}=9 \times 10^{n-1}\),
\({\color{Red}{(注意a_1的值是否满足a_{n}=9 \times 10^{n-1}(n \geq 2)}}\)
\(\therefore a_{n}=\left\{\begin{array}{lr}
8, & n=1 \\
9 \times 10^{n-1}, & n \geq 2
\end{array}\right.\).
【典题2】已知数列\(\{a_n\}\)的前\(n\)项和\(S_n\),满足\(a_2=-4\),\(2S_n=n(a_n-7)\),求\(a_1\)和数列\(\{a_n\}\)的通项公式.
【解析】(1)在\(2S_n=n(a_n-7)\)中,
当\(n=1\)时,\(2S_1=a_1-7\)\(⇒2a_1=a_1-7⇒a_1=-7\);
由\(2S_n=n(a_n-7)\)①得,
\(2 S_{n+1}=(n+1)\left(a_{n+1}-7\right)\)②,
由②-①可得,\(2 a_{n+1}=(n+1) a_{n+1}-n a_{n}-7\),
化简得\((n-1) a_{n+1}-n a_{n}=7\),
当\(n≥2\)时,有\(\dfrac{a_{n+1}}{n}-\dfrac{a_{n}}{n-1}=\dfrac{7}{n(n-1)}=7\left(\dfrac{1}{n-1}-\dfrac{1}{n}\right)\),
\({\color{Red}{(此处利用裂项\dfrac{1}{n(n-1)}=\dfrac{1}{n-1}-\dfrac{1}{n})}}\)
\(\therefore \dfrac{a_{n+1}}{n}-\dfrac{a_{2}}{1}\)
\(=\left(\dfrac{a_{n+1}}{n}-\dfrac{a_{n}}{n-1}\right)+\left(\dfrac{a_{n}}{n-1}-\dfrac{a_{n-1}}{n-2}\right)+\cdots \cdots+\left(\dfrac{a_{3}}{2}-\dfrac{a_{2}}{1}\right)\)\({\color{Red}{(累加法)}}\)
\(=7\left(\dfrac{1}{n-1}-\dfrac{1}{n}\right)+7\left(\dfrac{1}{n-2}-\dfrac{1}{n-1}\right)+\cdots \ldots+7\left(\dfrac{1}{1}-\dfrac{1}{2}\right)\)
\(=7\left(1-\dfrac{1}{n}\right)=\dfrac{7(n-1)}{n}\)
\(\therefore \dfrac{a_{n+1}}{n}=\dfrac{a_{2}}{1}+\dfrac{7(n-1)}{n}=-4+\dfrac{7(n-1)}{n}=\dfrac{3 n-7}{n}\)
\(\therefore a_{n+1}=3 n-7(n \geq 2)\),
\({\color{Red}{(n≥2不能漏,注意所得结论的前提)}}\)
故\(a_n=3n-10(n≥3)\),
\({\color{Red}{(此时注意n的取值改为n≥3)}}\)
又\(a_1=-7\),\(a_2=-4\)也都符合上式,
所以\(a_n=3n-10(n∈N^*)\).
【点拨】若已知条件已知\(S_n\)或者\(S_n\)与\(a_n\)的关系式,均可以利用\(a_{n}=\left\{\begin{array}{lr}
S_{1}, & n=1 \\
S_{n}-S_{n-1}, & n \geq 2
\end{array}\right.\)求解数列的通项公式\(a_n\).
巩固练习
1(★★)已知数列\(\{a_n\}\)的前\(n\)项和\(S_n\)满足\(S_n=n^2+n-1\),求数列\(\{a_n\}\)的通项公式.
2(★★)已知无穷数列\(\{a_n\}\)的前\(n\)项和\(S_n\),并且\(a_n+S_n=1\),求\(\{a_n\}\)的通项公式.
3(★★★)设数列\(\{a_n\}\)的前\(n\)项和\(S_n\),已知\(a_1=2\),\(a_2=8\),\(S_{n+1}+4 S_{n-1}=5 S_{n}\)\((n \geq 2)\),求数列\(\{a_n\}\)的通项公式;
参考答案
1.\(a_{n}=\left\{\begin{array}{c}
1, n=1 \\
2 n, n \geq 2
\end{array}\right.\)
2.\(a_{n}=\left(\dfrac{1}{2}\right)^{n}\)
3.\(a_{n}=2^{2 n-1}\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号