专题 圆锥曲线定值问题

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

选择性必修第一册同步提高，难度4颗星！

模块导图

知识剖析

定值问题描述

在圆锥曲线中，某些几何量在特定的关系结构中，不受相关变元的制约而恒定不变，则称该变量具有定值特征.
\({\color{Red}{ Eg}}\)
①一个球在水平面上无论怎么滚动，球心到水平面的距离都是半径长；
②椭圆上一动点\(P\)到两焦点\(F_1,F_2\)的距离之和\(PF_1+PF_2\)为一定值；
 

定值问题常见解题方法

定值问题往往涉及到一连串的“运动变化”，要确定某几何量的定值，我们要先理解题意，明确“变化的源头”，再找到源头与含定值特征的几何量之间的代数或几何关系，来确定解题的突破口.
 

参数法

把相关几何量用曲线里的参变量表示，再证明结论与求参数无关；
\({\color{Red}{ 解题步骤}}\) 引进参数--列出关系式--化简消参，求出定值.
 

由特殊到一般法

把相关几何量的变元特殊化，在特例中求出几何量的定值，再证明结论与特定状态无关.
 

几何法

根据几何关系确定相关几何量的不变.
 

经典例题

【方法一】参数法

【典题1】已知椭圆\(\dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)的左焦点\(F_1 (－1 ,0)\)，长轴长与短轴长的比是\(2 : \sqrt { 3 }\)．
(1)求椭圆的方程；
(2)过\(F_1\)作两直线\(m ,n\)交椭圆于\(A ,B ,C ,D\)四点，若\(m⊥n\)，求证：\(\dfrac { 1 } { | A B | } + \dfrac { 1 } { | CD | }\)为定值．

【解析】 (1)过程略，所求椭圆方程为\(\dfrac { x ^ { 2 } } { 4 } + \dfrac { y ^ { 2 } } { 3 } = 1\)；
(2)证明：当直线\(m\)斜率不存在时，
此时\(|AB|=3\),\(|CD|=4\)，\(\dfrac { 1 } { | A B | } + \dfrac { 1 } { | CD | }= \dfrac { 1 } { 3 } + \dfrac { 1 } { 4 } = \dfrac { 7 } { 12 }\)．
当直线\(m\)斜率存在时，设直线\(m\)的方程为\(y=k(x+1)(k≠0)\)．
由\(\begin{cases} { y = k ( x + 1 ) } \\ { \dfrac { x ^ { 2 } } { 4 } + \dfrac { y ^ { 2 } } { 3 } = 1 } \end{cases}\)，得\((3+4k^2 ) x^2+8k^2 x+4k^2－12=0\)．
设\(A(x_1 ,y_1)\),\(B(x_2 ,y_2)\)，
则有\(x _ { 1 } + x _ { 2 } = - \dfrac { 8 k ^ { 2 } } { 3 + 4 k ^ { 2 } }\)，\(x _ { 1 } x _ { 2 } = \dfrac { 4 k ^ { 2 } - 12 } { 3 + 4 k ^ { 2 } }\)，
\(| A B | = \sqrt { ( 1 + k ^ { 2 } ) [ ( x _ { 1 } + x _ { 2 } ) ^ { 2 } - 4 x _ { 1 } x _ { 2 } ] }\)
\(= \sqrt { ( 1 + k ^ { 2 } ) [ ( - \dfrac { 8 k ^ { 2 } } { 3 + 4 k ^ { 2 } } ) ^ { 2 } - 4 \times \dfrac { 4 k ^ { 2 } - 12 } { 3 + 4 k ^ { 2 } } }\)
\(= \dfrac { 12 ( 1 + k ^ { 2 } ) } { 3 + 4 k ^ { 2 } }\)
\({\color{Red}{(求AB 用弦长公式) }}\)
\(∵m⊥n\)，\(∴\)直线\(n\)的方程为\(y = - \dfrac { 1 } { k } ( x + 1 )\)
同理\(| C D | = \dfrac { 12 ( 1 + k ^ { 2 } ) } { 3 k ^ { 2 } + 4 }\)． \({\color{Red}{ (同理可得，故整体计算量不太大)}}\)
所以\(\dfrac { 1 } { | A B | } + \dfrac { 1 } { | C D | } = \dfrac { 3 + 4 k ^ { 2 } } { 12 ( 1 + k ^ { 2 } ) } + \dfrac { 3 k ^ { 2 } + 4 } { 12 ( 1 + k ^ { 2 } ) }\)
\(= \dfrac { 7 ( 1 + k ^ { 2 } ) } { 12 ( 1 + k ^ { 2 } ) } = \dfrac { 7 } { 12 }\)．
综上\(\dfrac { 1 } { | A B | } + \dfrac { 1 } { | C D | }\)为定值\(\dfrac { 7 } { 12 }\)．
【点拨】
① 定值问题往往涉及到“运动变化”，我们一定要找到其“源头”.我们是如下思考的

这样就找到了“源头”，故想到用\(k\)表示线段\(AB,CD\)长度；找源头的方式决定了引入的参数；
② 本题采取参数法，\(AB,CD\)显然可理解为直线与椭圆的弦长，故用弦长公式表示线段，当直线\(m\)斜率\(k\)存在时，\(\dfrac { 1 } { | A B | } + \dfrac { 1 } { | C D | }\)表示成关于参数\(k\)的式子\(f(k)\)，则证明\(\dfrac { 1 } { | A B | } + \dfrac { 1 } { | C D | }\)为定值，即证明\(f(k)\)为常数便可；
③ 若本题是一道非解答题，利用特殊法(即\(k\)不存在时)就很容易得到\(\dfrac { 1 } { | A B | } + \dfrac { 1 } { | C D | }\)为定值\(\dfrac { 7 } { 12 }\).
 

【典题2】 椭圆\(C : \dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)的离心率为\(\dfrac { 3 } { 5 }\)，\(P(m ,0)\)为\(C\)的长轴上的一个动点，过\(P\)点斜率为\(\dfrac { 4} { 5 }\)的直线\(l\)交\(C\)于\(A\)、\(B\)两点．当\(m=0\)时，\(\overrightarrow{P A} \cdot \overrightarrow{P B}=-\dfrac{41}{2}\).
(1)求\(C\)的方程； \(\qquad \qquad\)(2)求证：\(|PA|^2+|PB|^2\)为定值．
【解析】(1)过程略，椭圆\(C\)的方程为\(\dfrac { x ^ { 2 } } { 25 } + \dfrac { y ^ { 2 } } { 16 } = 1\)；
(2)依题意\(l\)的方程为\(x = \dfrac { 5 } { 4 } y + m\)，
代入\(\dfrac { x ^ { 2 } } { 25 } + \dfrac { y ^ { 2 } } { 16 } = 1\)，并整理得\(25y^2+20my+8(m^2-25)=0\)．
设\(A(x_1 ,y_1)\),\(B(x_2 ,y_2)\)，
则\(|PA|^2=(x_1-m)^2+y_1^2=\dfrac{41}{16} y_1^2\)，
同理\(|PB|^2=\dfrac{41}{16}y_2^2\)．
\(|PA|^2+|PB|^2=\dfrac{41}{16}(y_1^2+y_2^2)=\dfrac{41}{16}[(y_1+y_2 )^2-2y_1 y_2]\)\(= \dfrac { 41 } { 16 } [ ( - \dfrac { 4 m } { 5 } ) ^ { 2 } - \dfrac { 16 ( m ^ { 2 } - 25 )} { 25 } ]= 41\)．
所以\(|PA|^2+|PB|^2\)是定值．
【点拨】
① 本题的“变化源头”是\(m\)，线段\(PA,PB\)的长度变化显然是由\(m\)的值决定的，故想到用\(m\)表示线段\(PA\)、\(PB\)，则\(m\)就是引入的参数；
② 本题采取参数法，线段\(PA\)、\(PB\)用两点间距离公式\(\sqrt { ( x _ { 1 } - x _ { 2 } ) ^ { 2 } + ( y _ { 1 } - y _ { 2 } ) ^ { 2 } }\)表示成\(x_A\),\(y_A\)与\(x_B\),\(y_B\)，进而\(|PA|^2+|PB|^2\)表示为关于\(m\)的式子\(f(m)\)，证明\(|PA|^2+|PB|^2\)是定值即证明\(f(m)\)是常数，与参数\(m\)无关.
③ 直线\(l\)的方程设为\(x = \dfrac { 5 } { 4 } y + m\)，降低了计算量.
 

【典题3】已知\(A\)、\(B\)是椭圆\(\dfrac { x ^ { 2 } } { 2 } + y ^ { 2 } = 1\)上的两点，且\(\overrightarrow{A F} = \lambda \overrightarrow{FB}\)，其中\(F\)为椭圆的右焦点．
(1)求实数\(λ\)的取值范围；
(2)在\(x\)轴上是否存在一个定点\(M\)，使得\(\overrightarrow{MA} \cdot \overrightarrow{MB}\)为定值？若存在，求出定值和定点坐标；若不存在，说明理由．
【解析】(1)由已知条件知：直线\(AB\)过椭圆右焦点\(F(1 ,0)\)．
当直线\(AB\)与\(x\)轴重合时，\(\lambda = 3 \pm 2 \sqrt { 2 }\)．
当直线\(AB\)不与\(x\)轴重合时，设\(AB:x=my+1\)，
代入椭圆方程，并整理得\((2+m^2 ) y^2+2my-1=0\)，
设\(A(x_1 ,y_1)\),\(B(x_2 ,y_2)\)，
由根与系数的关系得\(y _ { 1 } + y _ { 2 } = \dfrac { - 2 m } { 2 + m ^ { 2 } }\)，\(y _ { 1 } y _ { 2 } = \dfrac { - 1 } { 2 + m ^ { 2 } }\)．
所以\(\dfrac { ( y _ { 1 } + y _ { 2 } ) ^ { 2 } } { y _ { 1 } y _ { 2 } } = \dfrac { - 4 m ^ { 2 } } { 2 + m ^ { 2 } } \in( - 4 , 0 ]\)．
又由\(\overrightarrow{A F} = \lambda \overrightarrow{FB}\)，得\(－y_1=λy_2\)，
所以\(\dfrac { ( y _ { 1 } + y _ { 2 } ) ^ { 2 } } { y _ { 1 } y _ { 2 } } = \dfrac { y _ { 1 } ^ { 2 } + y _ { 2 } ^ { 2 } + 2 y _ { 1 } y _ { 2 } } { y _ { 1 } y _ { 2 } }\)
\(= -\lambda - \dfrac { 1 } { \lambda } + 2 \in ( - 4 , 0 ]\)，
解之得\(3 - 2 \sqrt { 2 } \lt \lambda \lt 3 + 2 \sqrt { 2 }\)．
综上，实数\(λ\)的取值范围是\([3-2\sqrt { 2 } ,3+2\sqrt { 2 }]\)．
(2)设\(M(a ,0)\)，
直线\(AB\)不与\(x\)轴重合时，
则\(\overrightarrow{MA} \cdot \overrightarrow{MB}=(x_1-a)(x_2-a)+y_1 y_2\)
\({\color{Red}{(向量常用坐标处理) }}\)
\(=(my_1+1-a)(my_2+1-a)+y_1 y_2\)
\(=(1+m^2)y_1 y_2+m(1-a)(y_1+y_2)+(1-a)^2= - \dfrac { 1 + m ^ { 2 } } { 2 + m ^ { 2 } } - \dfrac { 2 m ^ { 2 } ( 1 - a ) } { 2 + m ^ { 2 } } + ( 1 - a ) ^ { 2 }\)
\(= \dfrac { - 1 + ( 2 a - 3 ) m ^ { 2 } } { 2 + m ^ { 2 } } + ( 1 - a ) ^ { 2 }\)为定值，
\({\color{Red}{ (\overrightarrow{MA} \cdot \overrightarrow{MB}为定值，即它不受m的影响)}}\)
所以\(\dfrac { - 1 } { 2 } = \dfrac { 2 a - 3 } { 1 }\)，解得\(a = \dfrac { 5 } { 4 }\)．
故存在定点\(M(\dfrac { 5 } { 4 },0)\)，使得\(\overrightarrow{MA} \cdot \overrightarrow{MB}\)为定值\(-\dfrac{7}{16}\)．
经检验，当\(AB\)与\(x\)轴重合时也成立，
\(∴\)存在定点\(M(\dfrac { 5 } { 4 },0)\)，使得\(\overrightarrow{MA} \cdot \overrightarrow{MB}\)为定值\(-\dfrac{7}{16}\)．
【点拨】
① 本题的“变化源头”是直线\(AB\)，若设直线\(AB\)方程为\(x=my+1\)，“源头”可理解为\(m\)，即不管\(m\)取任何值，\(\overrightarrow{MA} \cdot \overrightarrow{MB}\)的值恒定不变，引入参数\(m\)；
② 若式子\(\dfrac { c + d x } { a + b x }\)是定值，不受\(x\)的影响，则有\(\dfrac { c } { a } = \dfrac { d } { b }\)；
③ 注意最后直线\(AB\)与\(x\)轴重合特殊情况的分析.
 

【典题4】一束光线从点\(F_1 (-1 ,0)\)出发，经直线\(l:2x-y+3=0\)上一点\(P\)反射后，恰好穿过点\(F_2 (1 ,0)\)．
(1)求点\(P\)的坐标；
(2)求以\(F_1 ,F_2\)为焦点且过点\(P\)的椭圆\(C\)的方程；
(3)设点\(Q\)是椭圆\(C\)上除长轴两端点外的任意一点，试问在\(x\)轴上是否存在两定点\(A,B\)，使得直线\(QA\)、\(QB\)的斜率之积为定值？若存在，请求出定值，并求出所有满足条件的定点\(A\)、\(B\)的坐标；若不存在，请说明理由．
【解析】(1)设\(F_1\)关于\(l\)的对称点为\(F(m ,n)\)，

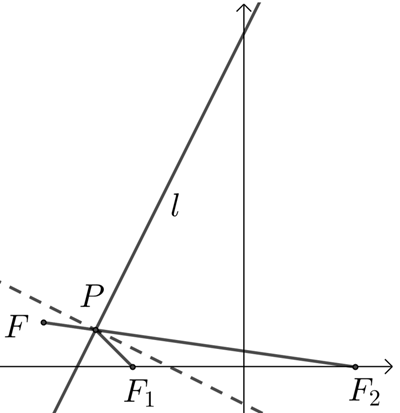
\({\color{Red}{(由反射的性质，可知点F ,P ,F_2三点共线) }}\)
则\(\dfrac { n } { m + 1 } = - \dfrac { 1 } { 2 }\)且\(2 \cdot \dfrac { m - 1 } { 2 } - \dfrac { n } { 2 } + 3 = 0\)，解得\(m = - \dfrac { 9 } { 5 } , \quad n = \dfrac { 2 } { 5 }\)，即\(F ( - \dfrac { 9 } { 5 } , \dfrac { 2 } { 5 } )\)，
易得直线\(PF\)方程为\(x+7y-1=0\)，
由\(\begin{cases} { x + 7 y - 1 = 0 } \\ { 2 x - y + 3 = 0 } \end{cases}\)，解得\(P ( - \dfrac { 4 } { 3 } , \dfrac { 1 } { 3 } )\)．
(2)因为\(PF_1=PF\)，根据椭圆定义，
得\(2a=PF_1+PF_2=PF+PF_2=FF_2\)
\(=\sqrt{((- \dfrac { 9 } { 5 } -1)^2+(\dfrac { 2} { 5 } -0)^2 }=2\sqrt2\)，
所以\(a=\sqrt2\)．又\(c=1\)，
所以\(b=1\)．所以椭圆\(C\)的方程为\(\dfrac { x ^ { 2 } } { 2 } + y ^ { 2 } = 1\)．
(3)\({\color{Red}{方法一 }}\) 假设存在两定点为\(A(s ,0)\),\(B(t ,0)\)，
则\(k _ { Q A } \cdot k _ { Q B } = \dfrac { y } { x - s } \cdot \dfrac { y } { x - t } = \dfrac { y ^ { 2 } } { x ^ { 2 } - ( s + t ) x + s t }\)
\({\color{Red}{(斜率常用斜率公式k = \dfrac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } }处理，若其是定值，则不受x ,y的影响，先想到消元) }}\)
又\(\dfrac { x ^ { 2 } } { 2 } + y ^ { 2 } = 1\)，
\(k _ { Q A } \cdot k _ { Q B } = \dfrac{1 - \dfrac { 1 } { 2 }x^2} { x^2-(s+t) x + st}\)\(= \dfrac { 1 - \dfrac { 1 } { 2 } x ^ { 2 } } { s t + x ^ { 2 } - (s + t ) x } = \dfrac { 2 - x ^ { 2 } } { 2 s t + 2 x ^ { 2 } - 2 ( s + t ) x }\)
若要\(\dfrac { 2 - x ^ { 2 } } { 2 s t + 2 x ^ { 2 } - 2 ( s + t ) x }\)是定值，
则要满足\(\begin{cases} { 2 ( s + t ) = 0 } \\ { \dfrac { 2 } { 2 s t } = \dfrac { - 1 } { 2 } } \end{cases} \Rightarrow \begin{cases} { s + t = 0 } \\ { s t = - 2 } \end{cases}\)，
解得\(\begin{cases} { s = \sqrt { 2 } } \\ { t = - \sqrt { 2 } } \end{cases}\)或\(\begin{cases} { s =- \sqrt { 2 } } \\ { t = \sqrt { 2 } } \end{cases}\)，
所以有且只有两定点\(( \sqrt { 2 } , 0 ) , ( - \sqrt { 2 } , 0 )\)，
使得\(k_{QA}\cdot k_{QB}\)为定值\(- \dfrac { 1 } { 2 }\)．
\({\color{Red}{方法二 }}\) 假设存在两定点为\(A(s ,0)\),\(B(t ,0)\)，
使得对于椭圆上任意一点\(Q(x ,y)\)(除长轴两端点)都有\(k_{QA}\cdot k_{QB}=k\)(\(k\)为定值)，
即\(\dfrac { y } { x - s } \cdot \dfrac { y } { x - t } = k \Rightarrow \dfrac { y ^ { 2 } } { x ^ { 2 } - ( s + t ) x + s t } = k\)，
将\(y ^ { 2 } = 1 - \dfrac { x ^ { 2 } } { 2 }\)代入并整理得
\(( k + \dfrac { 1 } { 2 } ) x ^ { 2 } - k ( s + t ) x + k s t - 1 = 0 \quad ( * )\)
\({\color{Red}{(相当要方程恒成立，与定点问题的方法类似) }}\)
由题意\((*)\)式对任意\(x∈(-\sqrt2,\sqrt2)\)恒成立，
所以\(\begin{cases} { k + \dfrac { 1 } { 2 } = 0 } \\ { k ( x + t ) = 0 } \\ { k s t - 1 = 0 } \end{cases}\)，解之得\(\begin{cases} { k = - \dfrac { 1 } { 2 } } \\ { s = \sqrt { 2 } } \\ { t = - \sqrt { 2 } } \end{cases}\)或\(\begin{cases} { k = - \dfrac { 1 } { 2 } } \\ { s = -\sqrt { 2 } } \\ { t = \sqrt { 2 } } \end{cases}\)．
所以有且只有两定点\(( \sqrt { 2 } , 0 ) , ( - \sqrt { 2 } , 0 )\)，
使得\(k_{QA}\cdot k_{QB}\)为定值\(- \dfrac { 1 } { 2 }\)．
【点拨】
① 方法一分式\(\dfrac { a _ { 1 } x ^ { 2 } + b _ { 1 } x + c _ { 1 } } { a _ { 2 } x ^ { 2 } + b _ { 2 } x + c _ { 2 } }\)是定值\(\Rightarrow \dfrac { a _ { 1 } } { a _ { 2 } } = \dfrac { b _ { 1 } } { b _ { 2 } } = \dfrac { c _ { 1 } } { c _ { 2 } }\)(即同项系数比相等)；
方法二利用方程恒成立的方法：式子\(ax^2+bx+c=0\)对\(x\)恒成立\(⇔a=0 ,b=0 ,c=0\)，设\(k_{QA}\cdot k_{QB}=k\)是关键；
② 点\(P\)处的切线\(PT\)平分\(△PF_1 F_2\)在点\(P\)处的外角.（椭圆的光学性质）

 

【典题5】如图，在平面直角坐标系\(xOy\)中，已知椭圆\(C : \dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)的离心率为\(\dfrac { \sqrt { 3 } } { 2 }\)，以椭圆\(C\)左顶点\(T\)为圆心作圆\(T:(x+2)^2+y^2=r^2 (r>0)\)，设圆\(T\)与椭圆\(C\)交于点\(M\)与点\(N\)．
(1)求椭圆\(C\)的方程；
(2)求\(\overrightarrow{TM} \cdot \overrightarrow{TN}\)的最小值，并求此时圆\(T\)的方程；
(3)设点\(P\)是椭圆\(C\)上异于\(M ,N\)的任意一点，且直线\(MP ,NP\)分别与\(x\)轴交于点\(R ,S ,O\)为坐标原点，求证：\(|OR|\cdot |OS|\)为定值．

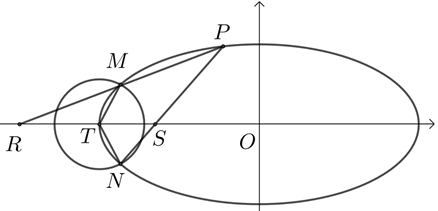
解：(1)过程略，椭圆\(C\)的方程为\(\dfrac { x ^ { 2 } } { 4 } + y ^ { 2 } = 1\)．
(2) 过程略，\(\overrightarrow{TM} \cdot \overrightarrow{TN}\)最小值为\(- \dfrac { 1 } { 5 }\)，圆\(T\)的方程为\(( x + 2 ) ^ { 2 } + y ^ { 2 } = \dfrac { 13 } { 25 }\)．
(3)
\({\color{Red}{ 分析：|OR|\cdot |OS|=|x_R x_S |，故可求出直线MP ,PN方程从而得到x_R ,x_S，如引入参数呢？}}\)
\({\color{Red}{ 方法一}}\) 设\(P(x_0 ,y_0)\)，\(M(x_1 ,y_1)\)，\(N(x_1 ,-y_1)\)，
则直线\(MP\)的方程为\(y - y _ { 0 } = \dfrac { y _ { 0 } - y _ { 1 } } { x _ { 0 } - x _ { 1 } } ( x - x _ { 0 } )\)，
令\(y=0\)，得\(x _ { R } = \dfrac { x _ { 1 } y _ { 0 } - x _ { 0 } y _ { 1 } } { y _ { 0 } - y _ { 1 } }\)，
同理\(x _ { s } = \dfrac { x _ { 1 } y _ { 0 } + x _ { 0 } y _ { 1 } } { y _ { 0 } + y _ { 1 } }\)，
\({\color{Red}{(把上式的y_1改为-y_1) }}\)
故\(x _ { R } \cdot x _ { s } = \dfrac { x _ { 1 } ^ { 2 } y _ { 0 } ^ { 2 } - x _ { 0 } ^ { 2 } y _ { 1 } ^ { 2 } } { y _ { 0 } ^ { 2 } - y _ { 1 } ^ { 2 } } (*)\)
又点\(M\)与点\(P\)在椭圆上，
故\(x_0^2=4(1-y_0^2)，x_1^2=4(1-y_1^2)\)，
代入\((*)\)式，
得\(x _ { R } \cdot x _ { B } = \dfrac { 4 ( 1 - y _ { 1 } ) y _ { 0 } ^ { 2 } - 4 ( 1 - y _ { 0 } ^ { 2 } ) y _ { 1 } ^ { 2 } } { y _ { 0 } ^ { 2 } - y _ { 1 } ^ { 2 } }= \dfrac { 4 ( y _ { 0 } ^ { 2 } - y _ { 1 } ^ { 2 } ) } { y _ { 0 } ^ { 2 } - y _ { 1 } ^ { 2 } } = 4\)．
所以\(|OR|\cdot|OS|=|x_R |\cdot|x_S |=|x_R x_S |=4\)为定值．
\({\color{Red}{方法二 }}\) 设\(M(2\cosθ ,\sinθ)\),\(N(2\cosθ ,－\sinθ)\)，
不妨设\(\sinθ>0\),\(P(2\cosα ,\sinα)\)，其中\(\sinα≠±\sinθ\)．
则直线\(MP\)的方程为\(y - \sin \alpha = \dfrac { \sin \alpha - \sin \theta } { 2 \cos \alpha - 2 \cos \theta } ( x - 2 \cos \alpha )\)，
令\(y=0\)，得\(x _ { R } = \dfrac { 2 ( \sin \alpha \cos \theta - \cos \alpha \sin \theta ) } { \sin \alpha - \sin \theta }\)，
同理\(x _ { S} = \dfrac { 2 ( \sin \alpha \cos \theta + \cos \alpha \sin \theta ) } { \sin \alpha + \sin \theta }\)，
\({\color{Red}{(把上式的\sin \theta改为-\sin \theta)}}\)
故\(x _ { R } \cdot x _ {S } = \dfrac { 4 ( \sin ^ { 2 } \alpha \cos ^ { 2 } \theta - \cos ^ { 2 } \alpha \sin ^ { 2 } \theta ) } { \sin ^ { 2 } \alpha - \sin ^ { 2 } \theta }\)．
所以\(|OR|\cdot|OS|=|x_R |\cdot|x_S |=|x_R x_S |=4\)为定值．
【点拨】参数法处理定值问题，找到了“运动源头”，如何引入参数需要根据题意，计算量是一衡量因素.本题源头是点\(P\)和点\(M\)，设\(P(x_0 ,y_0)\)，\(M(x_1 ,y_1)\)是最常见；方法二由椭圆的参数方程设为\(M(2\cosθ ,\sinθ)\),\(P(2\cosα ,\sinα)\)，引入参数比方法一少，计算量差不多吧！引入参数要注意参数的几何意义.
 

【方法二】“由特殊到一般”法

【典题1】已知双曲线\(C : \dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)，\(F_1、F_2\)分别是它的左、右焦点，\(A(－1 ,0)\)是其左顶点，且双曲线的离心率为\(e=2\)．设过右焦点\(F_2\)的直线\(l\)与双曲线\(C\)的右支交于\(P、Q\)两点，其中点\(P\)位于第一象限内．
(1)求双曲线的方程；
(2)若直线\(AP、AQ\)分别与直线\(x=\dfrac{1}{2}\)交于\(M、N\)两点，证明\(\overrightarrow{M F _ { 2 }} \cdot \overrightarrow{N F _ { 2 }}\)为定值；
(3)是否存在常数\(λ\)，使得\(∠PF_2 A=λ∠PAF_2\)恒成立？若存在，求出\(λ\)的值，若不存在，请说明理由．
【解析】(1)过程略，双曲线\(C\)的方程为\(x ^ { 2 } - \dfrac { y ^ { 2 } } { 3 } = 1\)．
(2)

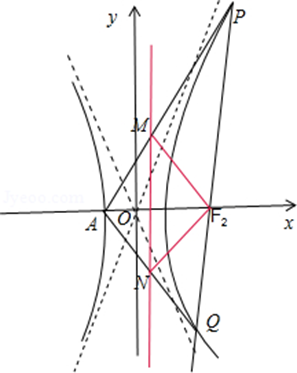
证明：设直线\(l\)的方程为\(x=ty+2\)，
\({\color{Red}{(源头是t，则用t表示\overrightarrow{M F _ { 2 }} \cdot \overrightarrow{N F _ { 2 }}，并证明其与t无关) }}\)
另设\(P(x_1 ,y_1)\),\(Q(x_2 ,y_2)\)，
联立\(\begin{cases} { 3 x ^ { 2 } - y ^ { 2 } = 3 } \\ { x = t y + 2 } \end{cases}\)，化为\((3t^2－1) y^2+12ty+9=0\)．
所以\(y _ { 1 } + y _ { 2 } = \dfrac { - 12 t } { 3 t ^ { 2 } - 1 } , y _ { 1 } y _ { 2 } = \dfrac { 9 } { 3 t ^ { 2 } - 1 }\)．
又直线\(AP\)的方程为\(y = \dfrac { y _ { 1 } } { x _ { 1 } + 1 } ( x + 1 )\)，
代入\(x = \dfrac { 1 } { 2 }\)，解得\(M ( \dfrac { 1 } { 2 } , \dfrac { 3 y _ { 1 } } { 2 ( x _ { 1 } + 1 )} )\)．
同理\(N ( \dfrac { 1 } { 2 } , \dfrac { 3 y _ { 2 } } { 2 ( x _ { 2 } + 1) } )\)．
\(∴\overrightarrow{M F _ { 2 } } = ( \dfrac { 3 } { 2 } , - \dfrac { 3 y _ { 1 } } { 2 ( x _ { 1 } + 1 ) } )\)，\(\overrightarrow{N F _ { 2 } } = ( \dfrac { 3 } { 2 } ,- \dfrac { 3 y _ { 2 } } { 2 ( x _ { 2 } + 1 ) } )\)．
\(∴\overrightarrow{M F _ { 2 } } \cdot\overrightarrow{N F _ { 2 } } = \dfrac { 9 } { 4 } + \dfrac { 9 y _ { 1 } y _ { 2 } } { 4 ( x _ { 1 } + 1 ) ( x _ { 2 } + 1 ) }\)\(= \dfrac { 9 } { 4 } [ 1 + \dfrac { y _ { 1 } y _ { 2 } } { ( t y _ { 1 } + 3 ) ( t y _ { 2 } + 3 ) } ]\)\(= \dfrac { 9 } { 4 } [ 1 + \dfrac { y _ { 1 } y _ { 2 } } { t ^ { 2 } y _ { 1 } y _ { 2 } + 3 t ( y _ { 1 } + y _ { 2 } ) + 9 } ]\)
\(= \dfrac { 9 } { 4 } [ 1 + \dfrac { \dfrac { 9 } { 3 t ^ { 2 } - 1 } } { t ^ { 2 } \times \dfrac { 9 } { 3 t ^ { 2 } - 1 } + 3 t \times \dfrac { - 12 t } { 3 t ^ { 2 } - 1 } + 9 } ] = \dfrac { 9 } { 4 } [ 1 - 1 ] = 0\)
(3) \({\color{Red}{ (分析：先通过特殊情况确定λ，再证明一般情况下也成立)}}\)
当直线\(l\)的方程为\(x=2\)时，解得\(P(2 ,3)\)．易知此时\(△AF_2 P\)为等腰直角三角形，
其中\(∠AF_2 P=\dfrac{π}{2}\),\(∠PAF_2=\dfrac{π}{4}\)，也即\(λ=2\)．
下证：\(∠AF_2 P=2∠PAF_2\)对直线\(l\)存在斜率的情形也成立．
\(\tan 2 \angle PAF_2 = \dfrac { 2 \tan \angle PAF_2 } { 1 - \tan ^ { 2 } \angle PAF_2}\)
\(=\dfrac { 2 k_{PA} } { 1 -k_{PA}^2 } = \dfrac { 2 \times \dfrac { y _ { 1 } } { x _ { 1 } + 1 } } { 1 - ( \dfrac { y _ { 1 } } { x _ { 1 } + 1 } ) ^ { 2 } }= \dfrac { 2 y _ { 1 } ( x _ { 1 } + 1 ) } { ( x _ { 1 } + 1 ) ^ { 2 } - y _ { 1 } ^ { 2 } }\)．
\(∵ x _ { 1 } ^ { 2 } - \dfrac { y _ { 1 } ^ { 2 } } { 3 } = 1\),\(∴ y _ { 1 } ^ { 2 } = 3 ( x _ { 1 } ^ { 2 } - 1 )\)
\(∴ \tan 2 \angle PAF_2 = \dfrac { 2 y _ { 1 } ( x _ { 1 } + 1 ) } { ( x _ { 1 } + 1 ) ^ { 2 } - 3 ( x _ { 1 } ^ { 2 } - 1 ) }\)\(= \dfrac { 2 y _ { 1 } ( x _ { 1 } + 1 ) } { - 2 ( x _ { 1 } + 1 ) ( x _ { 1 } - 2 ) } = - \dfrac { y _ { 1 } } { x _ { 1 } - 2 }\)
\(∴ \tan \angle PAF_2= - k _ { PF _ { 2 } } = - \dfrac { y _ { 1 } } { x _ { 1 } - 2 } = \tan 2 \angle PAF_2\)
\(∴\)结合正切函数在\(( 0 , \dfrac { \pi } { 2 } ) \cup ( \dfrac { \pi } { 2 } , \pi )\)上的图象可知\(∠AF_2 P=2∠PAF_2\)．
【点拨】
① 第三问本质是证明\(\dfrac { ∠AF_2 P } { \angle PAF_2 }\)是定值，本题采取了“由特殊到一般法”，思路是：在直线斜率不存在的特殊情况下易得\(λ=2\)，再证明\(∠AF_2 P=2∠PAF_2\)对直线\(l\)存在斜率的情形也成立；不采取特殊情况得到\(λ=2\)，往下的思路是很难想到的；
② 关于角度的问题，我们较容易想到解三角形的知识点，本题要证明\(∠AF_2 P=2∠PAF_2\)，思路是：\(∠AF_2 P=2∠PAF_2\)\(⇔ \tan∠AF_2 P=\tan2∠PAF_2 = \dfrac { 2 \tan∠PAF_2 } { 1 - \tan ^ { 2 }∠PAF_2}\)\(\Rightarrow - k _ { P F _ { 2 } } = \dfrac { 2 k _ {P A } } { 1 - k _ { PA } ^ { 2 } }\)，角度问题转化为斜率问题是常见思路.
 

【方法三】几何法

【典题1】已知抛物线\(C:y^2=2px(p>0)\)经过点\((2 ,-2\sqrt2)\)．
(1)求抛物线\(C\)的方程及其相应准线方程；
(2)过点\(E(2 ,0)\)作斜率为\(k_1 ,k_2\)的两条直线分别交抛物线于\(M ,N\)和\(P ,Q\)四点，其中\(k_1+k_2=1\)．设线段\(MN\)和\(PQ\)的中点分别为\(A ,B\)，过点\(E\)作\(ED⊥AB\)，垂足为\(D\)．证明：存在定点\(T\)，使得线段\(TD\)长度为定值．

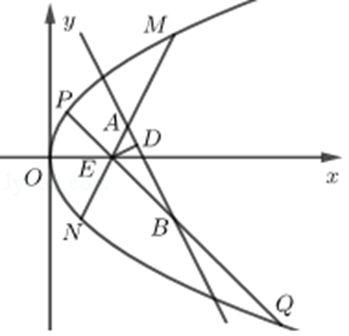
【解析】(1)过程略，抛物线的方程为\(y^2=4x\)，准线方程为\(x=－1\)；
(2)证明：设\(MN：y=k_1 (x－2)\),\(PQ：y=k_2 (x－2)\)，
由\(\begin{cases} { y = k _ { 1 } ( x - 2 ) } \\ { y ^ { 2 } = 4 x } \end{cases}\)可得\(k_1^2 x^2－(4+4k_1^2)x+4k_1^2=0\)，
可得\(x _ { A } = \dfrac { x _ { 1 } + x _ { 2 } } { 2 } = \dfrac { 4 + 4 k _ { 1 } ^ { 2 } } { 2 k _ { 1 } ^ { 2 } } = 2 + \dfrac { 2 } { k _ { 1 } ^ { 2 } }\)，\(y _ { A } = k _ { 1 } ( x _ { A } - 2 ) = \dfrac { 2 } { k _ { 1 } }\)
即\(A ( 2 + \dfrac { 2 } { k _ { 1 } ^ { 2 } } , \dfrac { 2 } { k _ { 1 } } )\)，同理可得\(B ( 2 + \dfrac { 2 } { k _ { 1 } ^ { 2 } } , \dfrac { 2 } { k _ { 2 } } )\)，
\(∴ k _ { A B } = \dfrac { \dfrac { 2 } { k _ { 1 } } - \dfrac { 2 } { k _ { 2 } } } { \dfrac { 2 } { k _ { 1 } ^ { 2 } } - \dfrac { 2 } { k _ { 2 } ^ { 2 } } } = k _ { 1 } k _ { 2 } ( k _ { 1 }+ k _ { 2 } ) = k _ { 1 } k _ { 2 }\)，
则直线\(AB\)的方程为\(y = k _ { 1 } k _ { 2 } ( x - 2 - \dfrac { 2 } { k _ { 1 } ^ { 2 } } ) + \dfrac { 2 } { k _ { 1 } }\)\(= k _ { 1 } k _ { 2 } ( x - 2 ) - \dfrac { 2 k _ { 2 } } { k _ { 1 } } + \dfrac { 2 } { k _ { 1 } } =k_1 k_2 (x－2)+2\)，
可得直线\(AB\)过定点\(F(2 ,2)\)，
则\(EF=2\)，又\(ED⊥FD\)，\({\color{Red}{ (隐圆，定弦定角模型)}}\)
\(∴D\)的轨迹是\((2 ,1)\)为圆心，\(1\)为半径的圆，
则存在定点\(T(2 ,1)\)，使得线段\(TD\)长度为定值\(1\)．
【点拨】
① “存在定点\(T\)，使得线段\(TD\)长度为定值”，意味着动点\(D\)到定点\(T\)是定长，即\(D\)的轨迹是以\(T\)为圆心的圆；
② 本题的“变化源头”是\(k_1\)(或\(k_2\))，由①的分析较为直接的思路是求出D的轨迹，具体作法：求出直线\(DE\)方程，再与直线\(AB\)联立求出点\(D\)的坐标(用\(k_1\)表示)，消参\(k_1\)后得到\(D\)的轨迹；这有个缺点是计算量较大；
③ 本题的解法属于几何法，在求出直线\(AB\)方程，有“意外收获”：它有定点\((2 ,2)\)，结合图象确定是“定弦定角的隐圆模型”，可知\(D\)的轨迹，确定定点\(T(2 ,1).\)
 

【典题2】如图，在平面直角坐标系\(xOy\)中，椭圆\(\dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)的左、右焦点分别为\(F_1 (－c ,0)\),\(F_2 (c ,0)\)．已知\((1 ,e)\)和\(( e , \dfrac { \sqrt { 3 } } { 2 } )\)都在椭圆上，其中\(e\)为椭圆的离心率．
(1)求椭圆的方程；
(2)设\(A ,B\)是椭圆上位于\(x\)轴上方的两点，且直线\(AF_1与\)直线\(BF_2\)平行，\(AF_2\)与\(BF_1\)交于点\(P\)．
(i)若\(A F _ { 1 } - B F _ { 2 } = \dfrac { \sqrt { 6 } } { 2 }\)，求直线\(AF_1\)的斜率；
(ii)求证：\(PF_1+PF_2\)是定值．

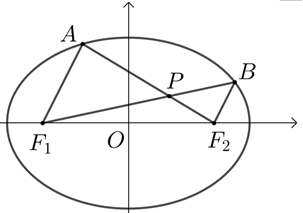
【解析】(1) 过程略，椭圆的方程为\(\dfrac { x ^ { 2 } } { 2 } + y ^ { 2 } = 1\)．
(2)解：由(1)得\(F_1 (－1 ,0)\),\(F_2 (1 ,0)\)，
又因为直线\(AF_1\)与直线\(BF_2\)平行，
所以设\(AF_1\)与\(BF_2\)的方程分别为\(x=my-1\),\(x=my+1\)．
设\(A(x_1 ,y_1)\),\(B(x_2 ,y_2)\),\(y_1>0\),\(y_2>0\)，
\(∴\)由\(\begin{cases} { \dfrac { x _ { 1 } ^ { 2 } } { 2 } + y _ { 1 } ^ { 2 } = 1 } \\ { x _ { 1 } = m y _ { 1 } - 1 } \end{cases}\)，可得\((m^2+2)y_1^2-2my_1－1=0\)．
\(∴ y _ { 1 } = \dfrac { m + \sqrt { 2 m ^ { 2 } + 2 } } { m ^ { 2 } + 2 }\)，\(y _ { 1 } = \dfrac { m - \sqrt { 2 m ^ { 2 } + 2 } } { m ^ { 2 } + 2 }\)(舍)，
\(∴ | A F _ { 1 } | = \sqrt { m ^ { 2 } + 1 } \times | 0 - y _ { 1 } | = \dfrac { \sqrt { 2 } ( m ^ { 2 } + 1 ) + m \sqrt { m ^ { 2 } + 1 } } { m ^ { 2 } + 2 }\)①
同理\(| B F _ { 2 } | = \dfrac { \sqrt { 2 } ( m ^ { 2 } + 1 ) - m \sqrt { m ^ { 2 } + 1 } } { m ^ { 2 } + 2 }\)②
(i)由①②得\(| A F _ { 1 } | - | B F _ { 2 } | = \dfrac { 2 m \sqrt { m ^ { 2 } + 1 } } { m ^ { 2 } + 2 }\)，\(∴ \dfrac { 2 m \sqrt { m ^ { 2 } + 1 } } { m ^ { 2 } + 2 } = \dfrac { \sqrt { 6 } } { 2 }\)，解得\(m=\sqrt2\)．
\(∴\)直线\(AF_1\)的斜率为\(\dfrac { 1 } { m } = \dfrac { \sqrt { 2 } } { 2 }\)．
(ii)证明：\(∵\)直线\(AF_1\)与直线\(BF_2\)平行，\({\color{Red}{(相似三角形的8字型) }}\)
\(∴\dfrac { P B } { P F _ { 1 } } = \dfrac { B F _ { 2 } } { A F _ { 1 } }\)，即\(P F _ { 1 } = \dfrac { A F _ { 1 } } { A F _ { 1 } + B F _ { 2 } } \times B F _ { 1 }\)．
由点\(B\)在椭圆上知，\(B F _ { 1 } + B F _ { 2 } = 2 \sqrt { 2 }\)，
\(∴ P F _ { 1 } = \dfrac { A F _ { 1 } } { A F _ { 1 } + B F _ { 2 } } \times ( 2 \sqrt { 2 } - B F _ { 2 } )\)．
同理\(P F _ { 2 } = \dfrac { B F _ { 2 } } { A F _ { 1 } + B F _ { 2 } } \times ( 2 \sqrt { 2 } - A F _ { 1 } )\)．
\(P F _ { 1 } + P F _ { 2 } = \dfrac { A F _ { 1 } } { A F _ { 1 } + B F _ { 2 } } \times ( 2 \sqrt { 2 } - B F _ { 2 } ) + \dfrac { B F _ { 2 } } { A F _ { 1 } + B F _ { 2 } } \times ( 2 \sqrt { 2 } - A F _ { 1 } )\)\(= 2 \sqrt { 2 } - \dfrac { 2 A F _ { 1 } \times B F_ { 2 } } { A F _ { 1 } + B F _ { 2 } }\)，
由①②得，\(A F _ { 1 } + B F _ { 2 } = \dfrac { 2 \sqrt { 2 } ( m ^ { 2 } + 1 ) } { m ^ { 2 } + 2 }\)，\(A F _ { 1 } \times B F _ { 2 } = \dfrac { m ^ { 2 } + 1 } { m ^ { 2 } + 2 }\)，
\(∴ P F _ { 1 } + P F _ { 2 } = \dfrac { 3 \sqrt { 2 } } { 2 }\)，\(∴PF_1+PF_2\)是定值．
【点拨】
① 本题采取了几何法，利用相似三角形的性质把\(PF_1+PF_2\)转化为\(AF_1 、BF_2\)的式子\(2 \sqrt { 2 } - \dfrac { 2 A F _ { 1 } \times B F_ { 2 } } { A F _ { 1 } + B F _ { 2 } }\)，再利用\(AF_1 、BF_2\)的关系确定其为定值；
② 本题另一思路：求出点\(A、B\)的坐标---求出直线\(AF_2 、BF_1\)的方程---求出点\(P\)的坐标---得到点\(P\)的轨迹方程---若证明其是椭圆即可证明\(PF_1+PF_2\)是定值，但计算量较大.
 

巩固练习

1 (★★★)如图，已知椭圆\(C _ { 1 } : \dfrac { x ^ { 2 } } { 4 } + y ^ { 2 } = 1\)，过抛物线\(C_2：x^2=4y\)焦点\(F\)的直线交抛物线于\(M ,N\)两点，连接\(NO，MO\)并延长分别交\(C_1\)于\(A，B\)两点，连接\(AB\)，\(△OMN\)与\(△OAB\)的面积分别记为\(S _ { \triangle O M N } , S _ {\triangle O A B }\)．则在下列命题中，正确的是(　　)

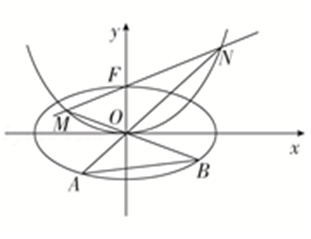
A．若记直线\(NO，MO\)的斜率分别为\(k_1，k_2\)，则\(k_1 k_2\)的大小是定值为\(-\dfrac{1}{4}\).
B．\(△OAB\)的面积\(S _ {\triangle O A B }\)是定值\(1\).
C．线段\(OA，OB\)长度的平方和\(|OA|^2+|OB|^2\)是定值\(5\).
D．设\(\lambda = \dfrac { S _ { \triangle O M N } } { S _ { \triangle O A B } }\)，则\(λ≥2\).

 

2(★★)在平面直角坐标系\(xoy\)中，已知焦点为\(F\)的抛物线\(x^2=4y\)上有两个动点\(A、B\)，且满足\(\overrightarrow{AF} =\lambda \overrightarrow{FB}\)，过\(A、B\)两点分别作抛物线的切线，设两切线的交点为\(M\)．
(1)求：\(\overrightarrow{OA} \cdot \overrightarrow{OB}\)的值； \(\qquad \qquad\)(2)证明\(\overrightarrow{FA} \cdot \overrightarrow{AB}\)为定值．
 
 

3(★★)已知，椭圆\(C\)过点\(A ( 1 , \dfrac { 3 } { 2 } )\)，两个焦点为\((－1 ,0)\),\((1 ,0)\)．
(1)求椭圆\(C\)的方程；
(2)\(E,F\)是椭圆\(C\)上的两个动点，如果直线\(AE\)的斜率与\(AF\)的斜率互为相反数，证明直线\(EF\)的斜率为定值，并求出这个定值．
 
 

4 (★★★)已知椭圆\(C : \dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)的长轴长为\(4\)，上顶点为\(A\)，左、右焦点分别为\(F_1 ,F_2\)，且\(∠F_1 AF_2=60°\)，\(O\)为坐标原点．
(1)求椭圆\(C\)的方程；
(2)设点\(M、N\)为椭圆\(C\)上的两个动点，若\(\overrightarrow{OM} \cdot \overrightarrow{ON}=0\)，问：点\(O\)到直线\(MN\)的距离\(d\)是否为定值？若是，求出\(d\)的值；若不是，请说明理由．
 
 

5(★★★)已知离心率为\(\dfrac { 2 \sqrt { 2 } } { 3 }\)的椭圆\(\dfrac { x ^ { 2 } } { a ^ { 2 } } + y ^ { 2 } = 1 ( a \gt 1 )\)，与直线\(l\)交于\(P ,Q\)两点，记直线\(OP\)的斜率为\(k_1\)，直线\(OQ\)的斜率为\(k_2\)．
(1)求椭圆方程；
(2)若\(k _ { 1 } \cdot k _ { 2 } = - \dfrac { 1 } { 9 }\)，则三角形\(OPQ\)的面积是否为定值？若是，求出这个定值；若不是，请说明理由．
 
 

6(★★★) 已知椭圆\(\dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)和圆\(O:x^2+y^2=b^2\), 过椭圆上一点\(P\)引圆\(O\)的两条切线，切点分别为\(A ,B\)．
(1)①若圆\(O\)过椭圆的两个焦点，求椭圆的离心率\(e\)；
②若椭圆上存在点\(P\)，使得\(∠APB=90°\)，求椭圆离心率\(e\)的取值范围；
(2)设直线\(AB\)与\(x\)轴、\(y\)轴分别交于点\(M ,N\)，求证：\(\dfrac { a ^ { 2 } } { |O N | ^ { 2 } } + \dfrac { b ^ { 2 } } { | 0 A | ^ { 2 } }\)为定值．
 
 

7(★★★)已知点\(M(－2 ,0)\),\(N(2 ,0)\)，点\(P\)满足：直线\(PM\)的斜率为\(k_1\)，直线PN的斜率为\(k_2\)，且\(k _ { 1 } \cdot k _ { 2 } = - \dfrac { 3 } { 4 }\)．
(1)求点\(P(x ,y)\)的轨迹\(C\)的方程；
(2)过点\(F(1 ,0)\)的直线\(l\)交曲线\(C\)于\(A ,B\)两点，问在\(x\)轴上是否存在点\(Q\)，使得\(\overrightarrow{OA} \cdot \overrightarrow{OB}\)为定值？若存在，求出点\(Q\)的坐标；若不存在，请说明理由．
 
 

8 (★★★)已知椭圆\(E:\dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)上动点\(P ,Q\)，\(O\)为原点：
(1)若\(|OP|^2+|OQ|^2=a^2+b^2\)，求证：\(|k_{OP}\cdot k_{OQ} |\)为定值；
(2)点\(B(0 ,b)\)，若\(BP⊥BQ\)，求证：直线\(PQ\)过定点；
(3)若\(OP⊥OQ\)，求证：直线\(PQ\)为定圆的切线．
 
 

9(★★★★)已知\(P\)是圆\(M：x^2+y^2+4x+4－4m^2=0(m>2)\)上任意一点，点\(N\)的坐标为\((2 ,0)\)，线段\(NP\)的垂直平分线交直线\(MP\)于点\(Q\)，当点\(P\)在圆\(M\)上运动时，点\(Q\)的轨迹为\(C\)．
(1)求出轨迹\(C\)的方程，并讨论曲线\(C\)的形状；
(2)当\(m=\sqrt5\)时，在\(x\)轴上是否存在一定点\(E\)，使得对曲线\(C\)的任意一条过\(E\)的弦\(AB\)，\(\dfrac { 1 } { [ E A ] ^ { 2 } } + \dfrac { 1 } { | E B | ^ { 2 } }\)为定值？若存在，求出定点和定值；若不存在，请说明理由．
 
 

参考答案

1.\(ABCD\)

2.\((1) -3\)\((2)0\)

3.\((1) \dfrac { x ^ { 2 } } { 4 } + \dfrac { y ^ { 2 } } { 3 } = 1\)\((2) \dfrac{1}{2}\)

4.\((1) \dfrac { x ^ { 2 } } { 4 } + \dfrac { y ^ { 2 } } { 3 } = 1\)\((2) \dfrac{2\sqrt{21}}{7}\)

5.\((1) \dfrac { x ^ { 2 } } {9 } + y ^ { 2 } = 1\)\((2) \dfrac{3}{2}\)

6.\((1)\dfrac { \sqrt { 2 } } { 2 } , \dfrac { \sqrt { 2 } } { 2 } \leq e \lt 1\)，\((2)\dfrac { a ^ { 2 } } { b ^ { 2 } }\)

7.\(( 1 ) \dfrac { x ^ { 2 } } { 4 } + \dfrac { y ^ { 2 } } { 3 } = 1 ( x \neq \pm 2 )\)\((2)Q ( \dfrac { 11 } { 8 } , 0 )\)

8.\((1) |k_{OP}⋅k_{OQ} |\)为定值\(\dfrac { b ^ { 2 } } { a ^ { 2 } }\)

\((2)\)直线\(PQ\)恒过定点\((0 , - \dfrac { b ( a ^ { 2 } - b ^ { 2 } ) } { a ^ { 2 } + b ^ { 2 } } )\)
\((3)\)提示：证明圆心到直线\(PQ\)的距离为定值

9.\((1)\)轨迹\(C\)是\(M ,N\)为焦点，以\(2m\)为长轴长的椭圆，方程为\(C : \dfrac { x ^ { 2 } } { m ^ { 2 } } + \dfrac { y ^ { 2 } } { m ^ { 2 } - 4 } = 1\);
\((2)\)定点为\(E ( \pm\dfrac { \sqrt { 30 } } { 3 } , 0 )\)，定值为\(6\).