专题 圆锥曲线中的三角形面积

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

选择性必修第一册同步提高，难度3颗星！

模块导图

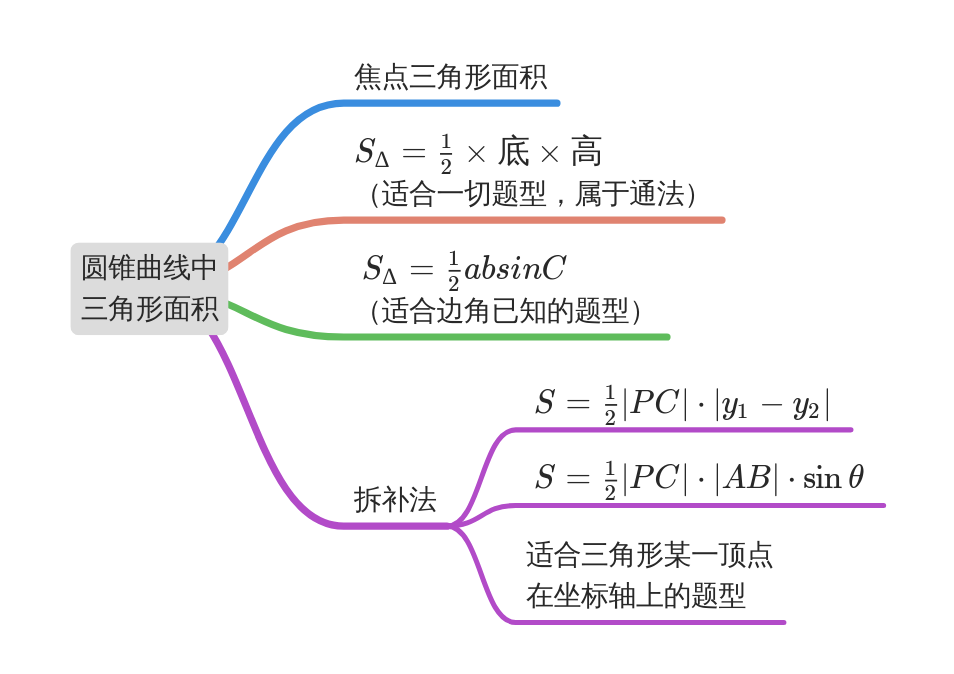
知识剖析

焦点三角形面积

椭圆\(\dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1\)的焦点三角形\(\triangle P F _ { 1 } F _ { 2 }\)面积\(S= b ^ { 2 } \tan \dfrac { \angle P } { 2 }\)，
双曲线\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1\)的焦点三角形\(\triangle P F _ { 1 } F _ { 2 }\)面积\(S = \dfrac { b ^ { 2 } } { \tan \frac {\angle P } { 2 } }\)(其中点\(P\)在椭圆或双曲线上).
 

直线与圆锥曲线中的三角形面积(以下以椭圆为例)

通法：底×高÷2

\(S _ { \triangle } = \dfrac { 1 } { 2 } \times 底 \times 高\)，适合一切题型，属于通法，但计算量会大些，
如图，\(S _ { \triangle PA B }= \dfrac { 1 } { 2 } \cdot A B \cdot P C\)(其中底为弦长\(AB\)，高为点\(P\)到直线\(AB\)的距离)

 

两边之积×夹角正弦值÷2

\(S _ { \triangle }= \dfrac { 1 } { 2 } a b \sin C\)，适合边角已知的题型

 

割补法

适合三角形某一顶点在坐标轴上的题型

情况1 同边

如图，点\(P\)在\(x\)轴上，直线\(AB\)交\(x\)轴于点\(C\)，
当\(A,B\)是在\(x\)轴异侧时，

\(S_{∆PAB}=S_{∆PAC}+S_{∆PBC}=\dfrac{1}{2}\cdot PC\cdot|y_A |+\dfrac{1}{2}\cdot PC\cdot|y_B |=\dfrac{1}{2}\cdot PC\cdot |y_A-y_B |\)

当\(A,B\)是在\(x\)轴同侧时，

\(S_{∆PAB}=S_{∆PAC}-S_{∆PBC}=\dfrac{1}{2}\cdot PC\cdot |y_A |-\dfrac{1}{2}\cdot PC \cdot |y_B |=\dfrac{1}{2}\cdot PC \cdot |y_A-y_B |\)
\({\color{Red}{PS }}\)不管\(A,B\)在\(x\)轴同侧还是异侧，公式\(S_{∆PAB}=\dfrac{1}{2}\cdot PC \cdot |y_A-y_B |\)依然成立.
若点在\(y\)轴类似可得\(S_{∆PAB}=\dfrac{1}{2}\cdot PC \cdot |x_A-x_B |\).
 

情况2 利用倾斜角

如图，点\(P\)在\(x\)轴上，直线\(AB\)的倾斜角为\(\theta\)，
当\(A,B\)是在\(x\)轴异侧时，
.
\(S_{∆PAB}=S_{∆PAC}+S_{∆PBC}=\dfrac{1}{2}\cdot PC\cdot AC\cdot \sin⁡(π-θ)+\dfrac{1}{2}\cdot PC\cdot BC\cdot \sin⁡θ=\dfrac{1}{2}\cdot PC\cdot AB\cdot \sin⁡θ\)
当\(A,B\)是在\(x\)轴同侧时，
.
\(S_{∆PAB}=S_{∆PAC}-S_{∆PBC}=\dfrac{1}{2}\cdot PC\cdot AC\cdot \sin⁡θ-\dfrac{1}{2}\cdot PC\cdot BC\cdot \sin⁡θ=\dfrac{1}{2}\cdot PC\cdot AB\cdot \sin⁡θ\)
\({\color{Red}{PS }}\)不管\(A,B\)是在\(x\)轴同侧还是异侧，公式\(S_{∆PAB}=\dfrac{1}{2}\cdot PC\cdot AB\cdot \sin⁡θ\)依然成立.(点在轴类似)
 

经典例题

焦点三角形面积

【典题1】设双曲线\(C : x ^ { 2 } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)的左、右焦点分别为\(F _ { 1 } , F _ { 2 }\)，\(P\)是\(C\)上一点，
且\(F_1 P⊥F_2 P\)，若\(△PF_1 F_2\)的面积为\(4\)，则离心率\(e=\)\(\underline{\quad \quad }\) .
【解析】\({\color{Red}{方法一 }}\) 由题意可知\(a=1\)，
设\(|PF_2 |=m ,|PF_1 |=n\)，可得\(|m－n|=2\)
\(∵△PF_1 F_2\)的面积为\(4\)，\(∴\dfrac{1}{2} mn=4⇒mn=8\)
\({\color{Red}{(遇到焦点三角形△PF_1F_2，想到定义和解三角形的内容)}}\)
\(∵F_1 P⊥F_2 P\)，\(∴m^2+n^2=4c^2\)，
\(∴(m-n)^2+2mn=4c^2⇒4c^2=4+16=20⇒c=\sqrt 5 \)
\(∴e = \dfrac { c } { a } = \sqrt { 5 }\).
\({\color{Red}{方法二 }}\) 由双曲线焦点三角形面积公式\(S = \dfrac { b ^ { 2 } } { \tan \frac {\angle P } { 2 } }\)，
\({\color{Red}{(椭圆焦点三角形面积公式S= b ^ { 2 } \tan \dfrac { \angle P } { 2 } ) }}\)
由题意可知\(\dfrac{b^2}{tan45°}=4\)，\(∴b=2 \)
又\(∵a=1\)，\(∴c=\sqrt5\)，\(∴e = \dfrac { c } { a } = \sqrt { 5 }\).
 

两边之积×夹角正弦值÷2

【典题2】已知直线\(l\)与双曲线\(E : \dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)的两条渐近线分别交于\(A(x_1 ,y_1 )\)、
\(B(x_2 ,y_2)\)两点，且\(x_1 x_2>0\)，若\(\overrightarrow{OA} \cdot \overrightarrow{OB} =-4\)，且\(△AOB\)的面积为\(2\sqrt3\)，则\(E\)的离心率为\(\underline{\quad \quad }\).

【解析】\(∵\overrightarrow{OA} \cdot \overrightarrow{OB} =-4\)，\(S _ { \triangle A O B } = 2 \sqrt { 3 }\)，
\(∴\begin{cases} { Q A \cdot O B \cdot \cos \angle A O B = - 4 } \\ { \dfrac { 1 } { 2 } O A \cdot O B \cdot \sin\angle A O B = 2 \sqrt { 3 } } \end{cases}\)，
\(∴tan∠AOB=-\sqrt3\),\(∴∠AOB=120°\)，
故\(∠AOx=60°\), 又直线\(OA\)方程为\(y=\dfrac{b}{a} x\),
\(∴ \dfrac { b } { a } = \tan 60 ^ { \circ } = \sqrt { 3 }\)，即\(b=\sqrt 3 a\)，
\(∴e = \dfrac { c } { a } = 2\).
【点拨】本题对“\(\overrightarrow{OA} \cdot \overrightarrow{OB} =-4\)”的处理是用数量积的定义得到\(OA⋅OB⋅cos∠AOB=-4\)，而\(△AOB\)的面积用到\(S_{△AOB}=\dfrac{1}{2}⋅OA⋅OB⋅sin∠AOB\)比较合理.
 

通法与割补法

【典题3】已知双曲线\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)的离心率为\(2\)，焦点到渐近线的距离等于\(\sqrt3\)，过右焦点\(F_2\)的直线\(l\)交双曲线于\(A、B\)两点，\(F_1\)为左焦点．
(1) 求双曲线的方程；
(2) 若\(△F_1 AB\)的面积等于\(6\sqrt2\)，求直线\(l\)的方程．
【解析】(1)过程略，\(x ^ { 2 } - \dfrac { y ^ { 2 } } { 3 } = 1\).
(2) \({\color{Red}{ 方法一}}\) 设\(A(x_1 ,y_1 )\),\(B(x_2 ,y_2 )\)，
当直线\(l\)的斜率不存在，则直线\(l\)的方程\(x=2\)，
此时易得\(S_{△F_1 AB}=12≠6\sqrt2\)，
故可设直线\(l\)的方程为\(y=k(x-2)\)，
由\(\begin{cases} { y = k ( x - 2 ) } \\ { x ^ { 2 } - \dfrac { y ^ { 2 } } { 3 } = 1 } \end{cases}\)，得\((k^2-3) x^2-4k^2 x+4k^2+3=0\)，
∵有两个交点，\(∴k≠±\sqrt3\)，且\(x _ { 1 } + x _ { 2 } = \dfrac { 4 k ^ { 2 } } { k ^ { 2 } - 3 }\),\(x _ { 1 } x _ { 2 } = \dfrac { 4 x ^ { 2 } + 3 } { k ^ { 2 } - 3 }\)，
\(| A B | = \sqrt { 1 + k ^ { 2 } } \cdot \sqrt { ( x _ { 1 } + x _ { 2 } ) ^ { 2 } - 4 x _ { 1 } x _ { 2 } }\)\(= \sqrt { 1 + k ^ { 2 } } \cdot \dfrac { 6 \sqrt { k ^ { 2 } + 1 } } { k ^ { 2 } - 3 }= \dfrac { 6 ( k ^ { 2 } + 1 ) } { k ^ { 2 } - 3 }\),
\(∵F_1 (-2 ,0)\)到直线\(l\)的距离\(d = \dfrac { 4 | k | } { \sqrt { 1 + k ^ { 2 } } }\)，
\(∴△F_1 AB\)的面积\(S = \dfrac { 1 } { 2 } \cdot d \cdot | A B | = \dfrac { 1 } { 2 } \cdot \dfrac { 4|k| } { \sqrt { 1 + k ^ { 2 } } } \cdot \dfrac { 6 ( k ^ { 2 } + 1 ) } { k ^ { 2 } - 3 }\)
\(12 | k | \cdot \dfrac { \sqrt { k ^ { 2 } + 1 } } { k ^ { 2 } - 3 } = 6 \sqrt { 2 }\)，
\({\color{Red}{(利用三角形面积公式S_∆=\dfrac { 1 } { 2 } ×底×高) }}\)
\(∴k^4+8k^2-9=0\)，解得\(k=±1\)，
\(∴\)所以直线\(l\)的方程为\(y=±(x-2)\)．
\({\color{Red}{方法二 }}\) 设\(A(x_1 ,y_1 )\),\(B(x_2 ,y_2 )\)，
同方法一可得\(k≠±\sqrt3\)，且\(x _ { 1 } + x _ { 2 } = \dfrac { 4 k ^ { 2 } } { k ^ { 2 } - 3 }\)，
\(∴|y_1－y_2 |=|k(x_1－x_2 )|\)\(= | k | \cdot \dfrac { \sqrt { ( 4 k ^ { 2 } ) ^ { 2 } - 4 ( k ^ { 2 } - 3 ) ( 4 k ^ { 2 } + 3 ) } } { | k ^ { 2 } - 3 | } = \dfrac { 6 | k | \sqrt{ | k ^ { 2 } + 1 } } { | k ^ { 2 } - 3 | }\)，
\(∴△F_1 AB\)的面积\(S= \dfrac { 1 } { 2 } | F _ { 1 } F _ { 2 } | | y _ { 1 } - y _ { 2 } |\)\(12 \cdot \dfrac { | k | \cdot | \sqrt { k ^ { 2 } + 1 } } { | k ^ { 2 } - 3 | } = 6 \sqrt { 2 }\)，
\({\color{Red}{(由于点F_1在x轴，利用S= \dfrac { 1 } { 2 } | F _ { 1 } F _ { 2 } | | y _ { 1 } - y _ { 2 } |) }}\)
化简得\(k^4+8k^2－9=0\)，解之得\(k^2=1\)，\(∴k=±1\)，
得直线\(l\)的方程为\(y=±(x-2)\)
【点拨】
① 注意分类讨论直线\(l\)的斜率是否存在；
② 因为直线过双曲线内的点，故不要看判别式\(∆\)是否大于\(0\)，但要注意\(k^2－3≠0⇒k≠±\sqrt3\)；
③ 第二问方法一是利用三角形面积公式\(S_∆=\dfrac { 1 } { 2 } ×底×高\)，得\(S=\dfrac { 1 } { 2 } \cdot |AB|\cdot d\)，其中以弦长\(AB\)为底，点\(F_1\)到直线\(AB\)的距离为高；方法二利用分拆三角形的方法得\(S= \dfrac { 1 } { 2 } | F _ { 1 } F _ { 2 } | | y _ { 1 } - y _ { 2 } |\)，此时要理解“不管\(AB\)是在\(x\)轴同侧还是异侧，公式依然成立”.
 

【典题4】过抛物线\(C：y^2=2px(p>0)\)的焦点\(F\)且倾斜角为\(\dfrac{π}{3}\)的直线交抛物线于\(A、B\)两点，交其准线于点\(C\)，且\(|AF|=|FC| ,|BC|=2\)．
(1)求抛物线\(C\)的方程；
(2)直线\(l\)交抛物线\(C\)于\(D、E\)两点，且这两点位于\(x\)轴两侧，与\(x\)轴交于点\(M\), 若\(\overrightarrow{OD} \cdot \overrightarrow{OE}=4\)，求\(S_{△DFO}+S_{△DOE}\)的最小值．

【解析】(1)过点\(A\)作抛物线准线的垂线，垂足为\(A_1\)，过点\(B\)作准线的垂线，垂足为\(B_1\)，
设准线与\(x\)轴交于点\(G\)，如图所示，

\(∵∠AFx=∠CBB_1=\dfrac{π}{3} ,BC=2\)，
\(∴BB_1=1\)，
\(∴BF=1\)，又点\(F\)为\(AC\)的中点，
\(∴AF=CF=BC+BF=3\)，
\(∴|GF|=\dfrac { 1 } { 2 } |AA_1 |=\dfrac { 1 } { 2 } |AF|=\dfrac { 3 } { 2 } ，∴p=\dfrac { 3 } { 2 }\)，
所以抛物线\(C\)的方程为\(y^2=3x\)．\({\color{Red}{(注意抛物线定义和平几知识的运用) }}\)
(2)设\(D(x_1 ,y_1)\),\(E(x_2 ,y_2)\), 设\(y_1>0 ,y_2<0\)，
\(l_{DE}：x=my+t\)，\({\color{Red}{ (这样设方程计算简便些)}}\)
联立得方程组\(\begin{cases} { x = m y + t } \\ { y ^ { 2 } = 3 x } \end{cases}\)，得\(y^2-3my-3t=0\)，
\(\begin{cases} { y _ { 1 } + y _ { 2 } = 3 m } \\ { y _ { 1 } y _ { 2 } = - 3 t } \end{cases}\)，
\(∴\overrightarrow{OD} \cdot \overrightarrow{OE}=x_1 x_2+y_1 y_2=\dfrac{y_1^2⋅y_2^2}{9}+y_1 y_2=4\)，
\({\color{Red}{ (曲线代换：利用抛物线方程消“x_1 x_2”)}}\)
\(∴y_1 y_2=3\)(舍去)或\(y_1 y_2=－12\)，
\(∴－3t=－12\)，\(∴t=4\)，即\(M(4 ,0)\)，
\(S _ {\triangle D F O } + S _ { \triangle D O E } = \dfrac { 1 } { 2 } | O F | \cdot y _ { 1 } + \dfrac { 1 } { 2 } | O M | \cdot ( y _ { 1 } - y _ { 2 } )\)
\(= \dfrac { 3 } { 8 } y _ { 1 } + 2 ( y _ { 1 } - y _ { 2 } ) = \dfrac { 19 } { 8 } y _ { 1 } + ( -2 y _ { 2 } )\)
\(\ge 2 \sqrt { \dfrac { 19 } { 8 } \times 2 | y _ { 1 } y _ { 2 } | } = 2 \sqrt { \dfrac { 19 } { 4 } \times 12 } = 2 \sqrt { 57 }\)，
(当且仅当\(\dfrac{19}{8} y_1=-2y_2\)，即\(y _ { 1 } = \dfrac { 8 \sqrt { 57 } } { 19 } , y _ { 2 } = - \dfrac { \sqrt { 57 } } { 2 }\)时，取到等号)
所以\(S _ {\triangle D F O } + S _ { \triangle D O E }\)的最小值为\(2 \sqrt { 57 }\)．

【点拨】在抛物线上设直线方程为\(l_{DE}：x=my+t\)较为常见，同时也配合上三角形面积\(S _ {\triangle D F O } + S _ { \triangle D O E } = \dfrac { 1 } { 2 } | O F | \cdot y _ { 1 } + \dfrac { 1 } { 2 } | O M | \cdot ( y _ { 1 } - y _ { 2 } )\).
 

【典题5】已知\(A、B\)是椭圆\(C: \dfrac { x ^ { 2 } } { a ^ { 2 } } + \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt b \gt 0 )\)的左，右顶点，\(B(2 ,0)\)，过椭圆\(C\)的右焦点\(F\)的直线交椭圆于点\(M ,N\)，交直线\(x=4\)于点\(P\)，且直线\(PA、PF、PB\)的斜率成等差数列，\(R\)和\(Q\)是椭圆上的两动点，\(R\)和\(Q\)的横坐标之和为\(2\)，\(RQ\)的中垂线交\(x\)轴于\(T\)点
(1)求椭圆\(C\)的方程；(2)求\(△MNT\)的面积的最大值.
【解析】(1)由题意知\(a=2\)，\(A(-2 ,0)\)，设\(P(4 ,y_0 ) ,F(c ,0)\)，
\(k _ { P A } = \dfrac { y _ { 0 } } { 6 } , k _ { P B } = \dfrac { y _ { 0 } } { 2 } , k _ { P F } = \dfrac { y _ { 0 } } { 4 - C }\),
依题意可知\(\dfrac { 2 y _ { 0 } } { 4 - c } = \dfrac { y _ { 0 } } { 6 } + \dfrac { y _ { 0 } } { 2 }\)，解得\(c=1\),
\(∴b^2=a^2-c^2=3\)，
\(∴\)椭圆\(C\)的方程\(\dfrac { x ^ { 2 } } { 4 } + \dfrac { y ^ { 2 } } { 3 } = 1\).
(2)设\(R(x_1 ,y_1 )\),\(Q(x_2 ,y_2)\)，
\(∵\)\(R\)和\(Q\)的横坐标之和为\(2\),\(∴x_1+x_2=2\)，
\(∵R、Q\)均在椭圆上，\(\dfrac { x _1^ { 2 } } { 4 } + \dfrac { y _ { 1 } ^ { 2 } } { 3 } = 1\)① \(\dfrac { x _2^ { 2 } } { 4 } + \dfrac { y _ { 2 } ^ { 2 } } { 3 } = 1\)② \({\color{Red}{(点差法) }}\)
① - ②得\(\dfrac { y _ { 1 } - y _ { 2 } } { x _ { 1 } - x _ { 2 } } = - \dfrac { 3 } { 2 ( y _ { 1 } + y _ { 2 } ) }\)，
设\(T(t ,0)\)，由中垂线性质得\(TR=TQ\)，即\(\sqrt { ( t - x _ { 1 } ) ^ { 2 } + y _ { 1 } ^ { 2 } } = \sqrt { ( t - x _ { 2 } ) ^ { 2 } + y _ { 2 } ^ { 2 } }\)，
化简得\(2 t = 2 + \dfrac { y _ { 1 } ^ { 2 } - y _ { 2 } ^ { 2 } } { x _ { 1 } - x _ { 2 } }\)\(= 2 + ( y _ { 1 } + y _ { 2 } ) \dfrac { y _ { 1 } - y _ { 2 } } { x _ { 1 } - x _ { 2 } } = 2 - \dfrac { 3 } { 2 } = \dfrac { 1 } { 2 }\)，
\(∴ t = \dfrac { 1 } { 4 }\)， 即\(T(\dfrac { 1 } { 4 },0)\).
设\(M(x_3 ,y_3 )\),\(N(x_4 ,y_4)\)，
直线\(MN:x=my+1\)与椭圆联立可得\((3m^2+4) y^2+6my-9=0\)，
\(y _ { 3 } + y _ { 4 } = \dfrac { 6 m } { 3 m ^ { 2 } + 4 } , y _ { 3 } y _ { 4 } = - \dfrac { 9 } { 3 m ^ { 2 } + 4 }\)，
\({\color{Red}{(因为直线MN过椭圆内一点F，故m可取全体实数R，不需要考虑判别式∆>0) }}\)
\(| y _ { 3 } - y _ { 4 } | ^ { 2 } = ( y _ { 3 } + y _ { 4 } ) ^ { 2 } - 4 y _ { 3 } y _ { 4 }\)\(= \dfrac { 36 m ^ { 2 } } { ( 3 m ^ { 2 } + 4 ) ^ { 2 } } + \dfrac { 36 } { 3 m ^ { 2 } + 4 } = 144 \dfrac { m ^ { 2 } + 1 } { ( 3 m ^ { 2 } + 4 ) ^ { 2 } }\)，
令\(n=m^2+1≥1\)，\({\color{Red}{(使用换元法降次，化难为简，函数思想注意自变量的取值范围) }}\)
则\(| y _ { 3 } - y _ { 4 } | ^ { 2 } = 144 \cdot \dfrac { n } { ( 3 n + 1 ) ^ { 2 } } = 144 \cdot \dfrac { 1 } { 9 n + \dfrac { 1 } { n } + 6 }\)
\(∵ y = 9 n + \dfrac { 1 } { n }\)在\([1 ,+∞)\)是递增的，\(∴y_{min}=10\)，
\({\color{Red}{(由对勾函数图像易得，由于n∈[1 ,+∞)不能用基本不等式) }}\)
\(| y _ { 3 } - y _ { 4 } | ^2_ { m a x } = 144 \cdot \dfrac { 1 } { 10 + 6 } = 9\)，即\(|y_3-y_4 |_{max}=3\)，
故\(S _ { m a x } = \dfrac { 1 } { 2 } \cdot F T ^ { \prime } \cdot | y _ { 3 } - y _ { 4 }|_{m a x} = \dfrac { 1 } { 2 } \times \dfrac { 3 } { 4 } \times 3 = \dfrac { 9 } { 8 }\).
【点拨】
① “\(R\)和\(Q\)的横坐标之和为\(2\)”这条件可想到“中点弦问题”的点差法，避免设直线\(RQ\)方程导致计算量增大；
② 本题最重要的想法是求\(△MNT\)的面积，用到了公式\(S=\dfrac{1}{2} \cdot FT \cdot|y_3-y_4 |\)，同时设直线方程为\(MN:x=my+1\)，联立方程时消\(x\)得到\(y\)的一元二次方程较易得到\(|y_3-y_4 |\)的表达式，大大减少了计算量，也避免直线斜率是否存在的分类讨论；
④ 求函数形如\(y = \dfrac { a _ { 1 } x ^ { 2 } + b _ { 1 } x + c _ { 1 } } { a _ { 2 } x ^ { 2 } + b _ { 2 } x + c _ { 2 } }\)最值问题，其中涉及对勾函数或基本不等式、换元法等内容，同时要注意自变量的取值范围，这是常考的题型.
 

巩固练习

1(★★)设\(F_1 ,F_2\)是椭圆\(\dfrac { x ^ { 2 } } { 9 } + \dfrac { y ^ { 2 } } { 6 } = 1\)的两个焦点，\(P\)是椭圆上的点，且\(|PF_1 |：|PF_2 |=2：1\)，则\(△F_1 PF_2\)的面积等于\(\underline{\quad \quad }\).
 

2(★★)过双曲线\(\dfrac { x ^ { 2 } } { 3 } - y ^ { 2 } = 1\)的右焦点F，作倾斜角为\(60°\)的直线\(l\), 交双曲线的渐近线于点\(A、B\)，\(O\)为坐标原点，则\(△OAB\)的面积为 \(\underline{\quad \quad }\).
 
3(★★)抛物线\(C：y^2=8x\)的焦点为\(F\)，\(N\)为准线上一点，\(M\)为\(y\)轴上一点，且\(\overrightarrow{NM} \cdot \overrightarrow{NF}=0\)，若线段\(MF\)的中点\(E\)在抛物线\(C\)上，则\(△MNF\)的面积为 \(\underline{\quad \quad }\).
 

4(★★)已知双曲线\(C: \dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)的离心率为\(\sqrt5\)，虚轴长为\(4\)．
(1)求双曲线的标准方程；
(2)过点\((0 ,1)\)，倾斜角为\(45°\)的直线\(l\)与双曲线\(C\)相交于\(A、B\)两点，\(O\)为坐标原点，求\(∆OAB\)的面积．
 

5(★★)椭圆\(C: \dfrac { x ^ { 2 } } { a ^ { 2 } } +\dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)过点\(A ( 1 , \dfrac { 3 } { 2 } )\)，离心率为\(\dfrac {1 } { 2 }\)，左、右焦点分别为\(F_1\),\(F_2\)，过\(F_1\)的直线交椭圆于\(C ,D\)两点．
(1)求椭圆\(C\)的方程；
(2)当\(△F_2 CD\)的面积为\(\dfrac { 12 \sqrt { 2 } } { 7 }\)时，求直线的方程．
 
 

6(★★★)如图，设椭圆的中心为原点\(O\)，长轴在\(x\)轴上，上顶点为\(A\)，左、右焦点分别为\(F_1 ,F_2\)，线段\(OF_1 ,OF_2\)的中点分别为\(B_1 ,B_2\)，且\(△AB_1 B_2\)是面积为\(4\)的直角三角形．
(1)求该椭圆的离心率和标准方程；
(2)过\(B_1\)作直线交椭圆于\(P ,Q\)两点，使\(PB_2⊥QB_2\)，求\(△PB_2 Q\)的面积．

 
 

7(★★★)已知椭圆\(C: \dfrac { x ^ { 2 } } { a ^ { 2 } } +\dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)的离心率为\(\dfrac { \sqrt { 3 } } { 2 }\)，\(F\)是椭圆的焦点，点\(A(0 ,－2)\)，直线\(AF\)的斜率为\(\dfrac { 2 \sqrt { 3 } } { 3 }\)，\(O\)为坐标原点．
(1)求椭圆\(C\)的方程；
(2)设过点\(A\)的直线与\(C\)相交于\(P、Q\)两点，当\(△OPQ\)的面积最大时，求\(l\)的方程．

 
 

8(★★★★)已知双曲线\(C\)的一个焦点为\((-\sqrt5 ,0)\)，且过点\(Q(2\sqrt5 ,2)\)．如图，\(F_1\)，\(F_2\)为双曲线的左、右焦点，动点\(P(x_0 ,y_0)(y_0≥1)\)在\(C\)的右支上，且\(∠F_1 PF_2\)的平分线与\(x\)轴、\(y\)轴分别交于点\(M(m ,0)(-\sqrt5<m<\sqrt5)、N\)，设过点\(F_1\),\(N\)的直线\(l\)与\(C\)交于\(D ,E\)两点．
(1) 求\(C\)的标准方程；
(2) 求\(△F_2 DE\)的面积最大值．

 
 

参考答案

1. \(2 \sqrt { 3 }\)
2. \(\dfrac { 3 \sqrt { 3 } } { 2 }\)
3. \(6 \sqrt { 2 }\)
4. \(x ^ { 2 } - \dfrac { y ^ { 2 } } { 4 } = 1 \quad ( 2 ) \dfrac { 4 } { 3 }\)
5. \(( 1 ) \dfrac { x ^ { 2 } } { 4 } + \dfrac { y ^ { 2 } } { 3 } = 1\)\(( 2 ) x - y + 1 = 0 或 x + y + 1 = 0\)
6. \(( 1 ) e = \dfrac { 2 } { 5 } , \dfrac { x ^ { 2 } } { 20 } + \dfrac { y ^ { 2 } } { 4 } = 1\quad ( 2 ) \dfrac { 16 } { 9 } \sqrt { 10 }\)
7. \((1)\dfrac { x ^ { 2 } } { 4 } + y ^ { 2 } = 1\quad ( 2 )y = \pm \dfrac { \sqrt { 7 } } { 2 } x - 2\)
8. \(( 1 ) \dfrac { x ^ { 2 } } { 4 } - y ^ { 2 } = 1 \quad ( 2 ) 4 \sqrt { 30 }\)