3.3 抛物线
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第一册同步提高,难度3颗星!
模块导图
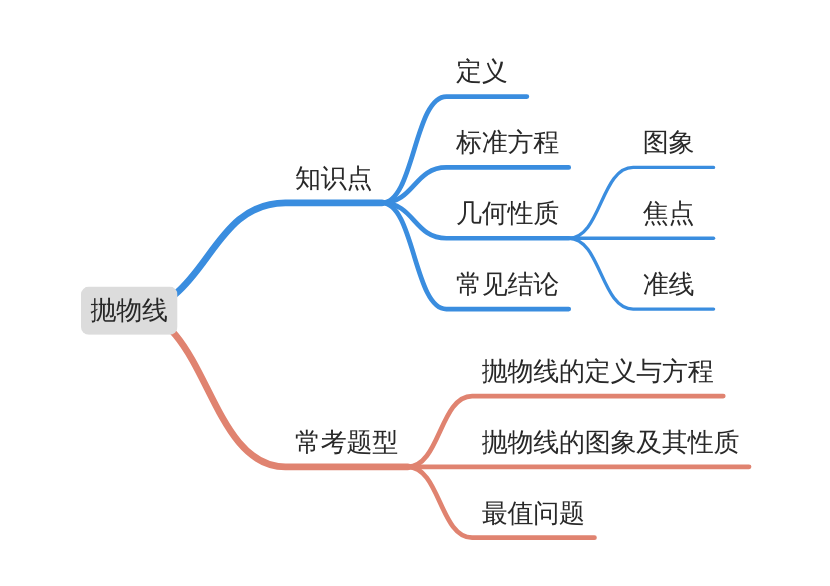
知识剖析
定义
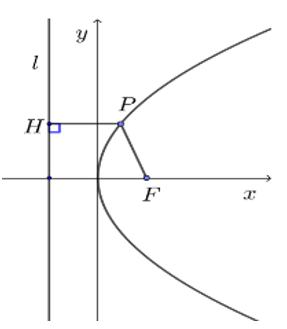
平面内与一个定点\(F\)和一条定直线\(l\)的距离相等的点的轨迹称为抛物线,定点\(F\)称为抛物线的焦点,定直线称为抛物线的准线.
如图,\(P\)在抛物线上,\(PH=PF\).
几何性质
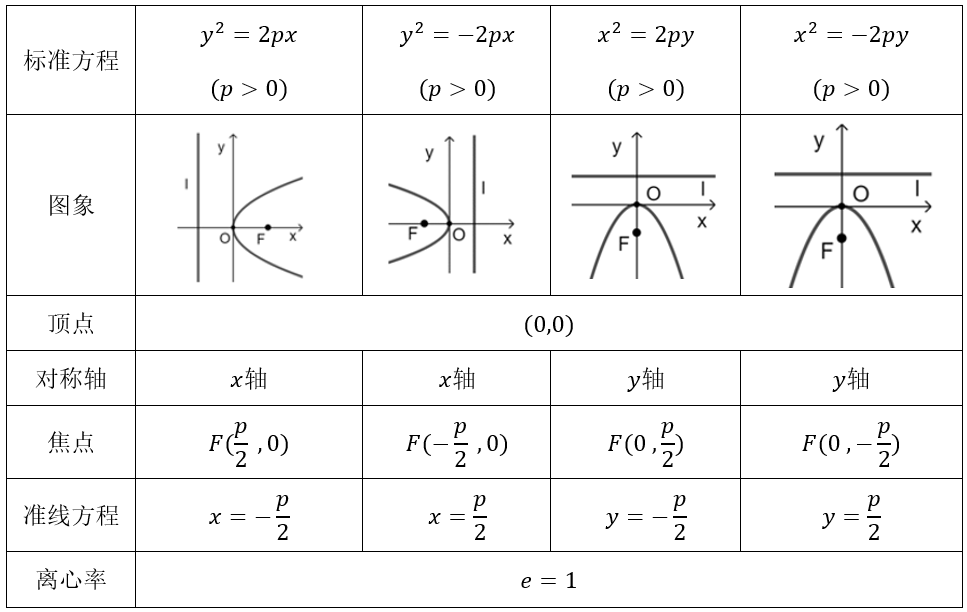
常见结论
①过抛物线的焦点作垂直于对称轴且交抛物线于\(A,B\)两点的线段,称为抛物线的“通径”,即\(|AB|=2p\).
②若\(A,B\)在抛物线\(y^2=2px\)上,\(F\)是焦点,则\(A F = x _ { A } + \dfrac { p } { 2 } , \quad A B = x _ { A } + x _ { B } + p\).
经典例题
【题型一】抛物线的定义与方程
【典题1】与圆\(( x - 2 ) ^ { 2 } + y ^ { 2 } = 1\)外切,且与直线\(x+1=0\)相切的动圆圆心的轨迹方程是\(\underline{\quad \quad}\) .
【解析】

由圆\(( x - 2 ) ^ { 2 } + y ^ { 2 } = 1\)可得:圆心\(F(2,0)\),半径\(r=1\).
设所求动圆圆心为\(P(x,y)\),
过点\(P\)作直线\(PM\)垂直直线\(l\),\(M\)为垂足.
则\(|P F | - r = | P M |\),可得\(| P F | = | P M | + 1\).
因此可得点\(P\)的轨迹是到定点\(F(2,0)\)的距离和到直线\(L:x=-2\)的距离相等的点的集合.
由抛物线的定义可知:
点的轨迹是抛物线,定点\(F(2,0)\)为焦点,定直线\(L:x=-2\)是准线.
所以抛物线的方程为\(y^2=8x\).
所以所求轨迹方程是\(y^2=8x\).
【点拨】
①直线\(l\)与圆\(O\)相切等价于圆心\(O\)到直线\(l\)的距离\(d=r\);
②根据抛物线定义求方程,要确定好焦点与准线.
巩固练习
1(★)到直线\(x=-2\)与到定点\(p(2,0)\)的距离相等的点的轨迹是( )
A.椭圆 \(\qquad \qquad \qquad \qquad\) B.圆 \(\qquad \qquad \qquad \qquad\) C.抛物线 \(\qquad \qquad \qquad \qquad\) D.直线
2 (★★)若点\(P\)到点\(F(4,0)\)的距离比它到直线\(x+5=0\)的距离少\(1\),则动点的轨迹方程是\(\underline{\quad \quad}\) .
参考答案
1.\(C\)
2.\(y^2=16x\)
【题型二】抛物线的图象及其性质
【典题1】设抛物线\(C : y ^ { 2 } = 8 x\)的焦点为\(F\),\(A\)是\(C\)上的一点且在第一象限,以\(F\)为圆心,以\(FA\)为半径的圆交\(C\)的准线于\(B,D\)两点,且三点\(A,F,B\)共线,则点\(A\)的横坐标为\(\underline{\quad \quad}\) .
【解析】

因为三点\(A,F,B\)共线,
所以\(AB\)为圆\(F\)的直径,则\(A D\perp B D\).
由抛物线定义知\(| A D | = | A F | = \dfrac { 1 } { 2 } | A B |\),
又抛物线\(C : y ^ { 2 } = 8 x\)的\(\dfrac { p } { 2 } = 2\),
在\(R t\triangle A D B\)中,可得\(| A D | = 4 | O F | = 8\).
设\(A\)的横坐标为\(x_0\),则\(| A D | = x _ { 0 } + 2 = 8\),即\(x_0=6\).
【点拨】
①在抛物线中,遇到过焦点的直线,特别要注意抛物线定义的运用;
②若\(A,B\)在抛物线\(y^2=2px\)上,\(F\)是焦点,则\(A F = x _ { A } + \dfrac { p } { 2 } , \quad A B = x _ { A } + x _ { B } + p\).
【典题2】已知抛物线\(C : y ^ { 2 } = 2 p x ( p \gt 0 )\)的焦点为\(F\),点\(M,N\)在抛物线上,且\(M,N,F\)三点共线点\(P\)在准线上,若\(\overrightarrow{PN}= \overrightarrow{NM}\),则\(\dfrac { p } { | M F | } =\)\(\underline{\quad \quad}\) .
【解析】

如图,分别过\(M,N\)作\(ME,NG\)垂直于抛物线的准线于\(E,G\),
由\(\overrightarrow{PN}= \overrightarrow{NM}\),得\(PN=NM\),
由抛物线定义可知\(N F = N G , \quad F M = M E\),
再由\(\triangle P N G \sim\triangle P M E\),
得\(\dfrac { P M } { M E } = \dfrac { P N } { N G } \Rightarrow \dfrac { P M } { M F } = \dfrac { P N} { N F } \Rightarrow \dfrac { P M } { M F } = \dfrac { \dfrac { 1 } { 2 } P M } { N F }\),
所以\(MN=2NF\),
则\(N F = \dfrac { 1 } { 3 } N M = \dfrac { 1 } { 6 } P M\),\(P F = P N + N F = \dfrac { 1 } { 2 } P M + \dfrac { 1 } { 6 } P M = \dfrac { 2 } { 3 } P M\).
所以\(\dfrac { p } { | M F | } = \dfrac { F K } { M E } = \dfrac { P F } { P M } = \dfrac { 2 } { 3 }\).
【点拨】
①本题主要利用了相似三角形的性质(字型)与抛物线的定义得到各线段的比值关系,平时解题中要多观察图象;
②题中线段过多,显得有些乱,其实在考试的非解答题中,遇到这类似问题,由于题目中没出现任一线段长度,确定\(\dfrac { p } { | M F | } = \dfrac { F K } { M E }\)后,可设某一线段等于一具体数值,比如本题设\(PN=1\)(其实令\(PN=6\)更有利于运算),进而求出其他线段长度,这样在考试时运算上显得从容些.
【典题3】已知抛物线\(C:y^2=4x\)的焦点为\(F\),准线为\(l\),\(P\)为\(C\)上一点,\(PQ\)垂直l于点\(Q\),\(M,N\)分别为\(PQ,PF\)的中点,\(MN\)与\(x\)轴相交于点\(R\),若\(∠NRF=60°\),则\(|FR|\)等于\(\underline{\quad \quad}\) .
【解析】

如图所示:连接\(MF,QF\),
因为\(y^2=4x\)的焦点为\(F\),准线为\(l\),\(P\)为\(C\)上一点,
所以\(FH=2,PF=PQ\)
\(∵M,N\)分别为\(PQ,PF\)的中点,\(∴MN∥QF\),
\(∵PQ\)垂直\(l\)于点\(Q\),\(∴PQ∥OR\),
\(∴\)四边形\(MQFR\)是平行四边形,\(∴FR=MQ\)
\(∵PQ=PF,∠NRF=60°\),\(∴△PQF\)为等边三角形,
\(∴MF⊥PQ\),
\(∴\)四边形\(MQHF\)是矩形,\(∴MQ=HF=2\)
\(∴FR=MQ=2\),
故答案为:\(2\).
【点拨】
①\(△PQF\)为等边三角形\(⇒\)三线合一:\(MF⊥PQ\);
②\(M,N\)分别为\(PQ,PF\)的中点\(⇒\)中位线:\(MN∥QF\).
【典题4】已知抛物线\(C\)的顶点为坐标原点 , 焦点\(F\)在\(x\)轴上 , 其准线为\(l\), 过\(F\)的直线交抛物线于\(M ,N\)两点 , 作\(MS⊥l ,NT⊥l\), 垂足分别为\(S ,T\).若\(\overrightarrow{MF} =3\overrightarrow{FN}\), 且\(△STF\)的面积为\(\dfrac{8\sqrt3}{3}\) , 则抛物线\(C\)的方程为( )
A.\(y^2=±x\) \(\qquad \qquad \qquad \qquad\) B.\(y^2=±2x\) \(\qquad \qquad \qquad \qquad\) C.\(y^2=±3x\) \(\qquad \qquad \qquad \qquad\) D.\(y^2=±4x\)
【解析】

如图所示 , 过点\(N\)作\(NH∥l\)交直线\(MS\)于点\(H\), 交\(x\)轴于点\(P\).
设点\(M(x_1 ,y_1)、N(x_2 ,y_2) ,\)
当焦点在\(x\)轴的正半轴时 , 设抛物线\(C:y^2=2px(p>0)\),
\(∵\overrightarrow{MF} =3\overrightarrow{FN}\), 且\(F(\dfrac{p}{2},0)\),
\(∴(\dfrac{p}{2}-x_1 ,-y_1)=3(x_2-\dfrac{p}{2} ,y_2)\),
\(∴\dfrac{p}{2}-x_1=3(x_2-\dfrac{p}{2}) ⇒x_1+3x_2=2p\) ①
\(∴-y_1=3y_2⇒y_1^2=9y_2^2⇒2px_1=18px_2⇒x_1=9x_2\) ②.
由①②可解得\(x_1=\dfrac{3p}{2} ,x_2=\dfrac{p}{6}\).
\(∴y_1^2=2px_1=3p^2⇒y_1=\sqrt3 p\),\(y_2^2=2px_2=\dfrac{p^2}{3}⇒y_2=-\dfrac{\sqrt3}{3}p\),
\(∴|ST|=y_1-y_2=\dfrac{4\sqrt3}{3} p\)
\(∴S_{△STF}=\dfrac{1}{2}⋅\dfrac{4\sqrt3}{3} p⋅p=\dfrac{8\sqrt3}{3}\), 解得\(p=2\),
此时抛物线\(C\)的方程为\(y^2=4x\).
同理 , 当焦点在\(x\)轴的负半轴时 , 可得\(p=-2\), 此时抛物线\(C\)的方程为\(y^2=-4x\).
综上所述 , 抛物线C的方程为\(y^2=±4x\).
故选:\(D\).
【点拨】
① 本题处理向量\(\overrightarrow{MF} =3\overrightarrow{FN}\)的方法是坐标法;
② 遇到“\(△STF\)的面积为\(\dfrac{8\sqrt3}{3}\)”,想到把\(△STF\)的面积用\(p\)表示,从而求出\(p\);关键在于\(|ST|=y_1-y_2\), 从而想到用\(p\)表示\(y_1 ,y_2\).
【典题5】已知\(F\)为抛物线\(C : y ^ { 2 } = 2 p x ( p \gt 0 )\)的焦点,\(K\)为\(C\)的准线与\(x\)轴的交点,点\(P\)在抛物线\(C\)上,设\(\angle K P F = \alpha , \angle P K F =\beta ,\angle P F K = \theta\),有以下个结论:
①\(\beta\)的最大值是\(\dfrac{\pi}{4}\);\(\qquad \qquad\)②\(\tan \beta = \sin \theta\);\(\qquad \qquad\)③存在点\(P\),满足\(\alpha = 2 \beta\).
其中正确结论的序号是\(\underline{\quad \quad}\) .
【解析】

①由于对称性,不妨设点\(P\)在第一象限,
设点\(P(m,n)\),则\(n ^ { 2 } = 2 p m\)(1),
当直线\(PK\)与抛物线相切时,可使\(\beta\)取得最大值.
可设直线方程为\(y = k ( x + \dfrac { p } { 2 } )\),
由\(\begin{cases} { y = k ( x + \dfrac { p } { 2 } ) } \\ { y ^ { 2 } = 2 p x } \end{cases}\),得\(k ^ { 2 } x ^ { 2 } + ( k ^ { 2 } p - 2 p ) x + \dfrac { p ^ { 2 } k ^ { 2 } } { 4 } = 0\),
则\(A = ( k ^ { 2 } p - 2 p ) ^ { 2 } - 4 k ^ { 2 } \cdot \dfrac { p ^ { 2 } k ^ { 2 } } { 4 } = 0 \Rightarrow k ^ { 2 } = 1 \Rightarrow k = \pm 1\)
因为\(\beta\)是锐角,所以\(\tan \beta = k = 1 \Rightarrow \beta = \dfrac { \pi } { 4 }\),故①正确
②过\(P\)作\(PQ\)垂直\(x\)轴于点\(Q\),
在\(R t \triangle P Q K\)中,\(\tan \beta = \dfrac { PQ } {KQ} = \dfrac { n } { m + \dfrac { p } { 2 } }\),
在\(R t \triangle P Q F\)中,\(\sin \theta = \sin\angle P F Q = \dfrac { P Q } {PF } = \dfrac { n } { m + \dfrac { p } { 2 } }\),
所以\(tan \beta = sin \theta\),即②正确;
③在\(R t \triangle PK F\)中,由正弦定理知\(\dfrac { P F } { \sin \beta } = \dfrac { K F } { \sin \alpha }\),
若\(\alpha = 2 \beta\),则\(\dfrac { m + \dfrac { p } { 2 } } { \sin \beta } = \dfrac { p } { 2 \sin \beta \cos \beta }\),解得\(m = \dfrac { p } { 2 } ( \dfrac { 1 } { \cos \beta } - 1 ) \gt 0\),
故存在点\(P\)符合题意,即③正确.
故答案为:①②③.
【点拨】
第一问是通过几何法确定直线\(PK\)与抛物线相切时,可使\(\beta\)取得最大值;第二问,涉及到三角函数\(tan \beta 、 sin \theta\)之类的,可想到构造直角三角形;第三问,是否存在点\(P\), 用了假设法确定\(m\)是否在自身范围之内,即\(m>0\)与否.
巩固练习
1(★★) 【多选题】抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.已知抛物线\(y^2=4x\)的焦点为\(F\),一束平行于\(x\)轴的光线\(l_1\)从点\(M(3,1)\)射入,经过抛物线上的点\(P(x_1,y_1)\)反射后,再经抛物线上另一点\(Q(x_2,y_2)\)反射后,沿直线\(l_2\)射出,则下列结论中正确的是( )
A.\(x_1 x_2=1\)\(\qquad \qquad\) B.\(k_PQ=-\dfrac{4}{3}\) \(\qquad \qquad\) C.\(|PQ|=\dfrac{25}{4}\)\(\qquad \qquad\) D.\(l_1\)与\(l_2\)之间的距离为\(4\)
2(★★) 如图过抛物线\(y^2=2px(p>0)\)的焦点\(F\)的直线依次交拋物线及准线于点\(A,B,C\),若\(|BC|=2|BF|\),且\(|AF|=3\),则\(p=\)( )
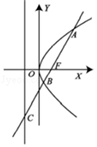
A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(\dfrac {3}{2}\) \(\qquad \qquad \qquad \qquad\) C.\(3\) \(\qquad \qquad \qquad \qquad\) D.\(6\)
3(★★★) 【多选题】已知抛物线\(x^2=\dfrac {1}{2} y\)的焦点为\(F\),\(M(x_1,y_1),N(x_2,y_2)\)是抛物线上两点,则下列结论正确的是( )
A.点\(F\)的坐标为\((\dfrac{1}{8},0)\)
B.若直线\(MN\)过点\(F\),则\(x_1 x_2=-\dfrac{1}{16}\)
C.若\(\overrightarrow{MF}=\lambda \overrightarrow{NF}\),则\(|MN|\)的最小值为\(\dfrac {1}{2}\)
D.若\(|MF|+|NF|=\dfrac {3}{2}\),则线段\(MN\)的中点\(P\)到\(x\)轴的距离为\(\dfrac {5}{8}\)
4 (★★)已知点\(A(0,4)\),抛物线\(C:x^2=2py(0<p<4)\)的准线为\(l\),点\(P\)在\(C\)上,作\(PH⊥l\)于\(H\),且\(|PH|=|PA|\),\(∠APH=120°\),则抛物线方程为\(\underline{\quad \quad}\) .
5(★★★) 如图 , 点\(A\)是曲线\(y=\sqrt{x^2+2}(y≤2)\)上的任意一点 ,\(P(0 ,-2) ,Q(0 ,2)\), 射线\(QA\)交曲线\(y=\dfrac{1}{8} x^2\)于\(B\)点 ,\(BC\)垂直于直线\(y=3\), 垂足为点\(C\).则下列判断:①\(|AP|-|AQ|\)为定值\(2\sqrt2\);②\(|QB|+|BC|\)为定值\(5\).其中正确的说法是( )

A.①②都正确 \(\qquad \qquad \qquad \qquad\) B.①②都错误 \(\qquad \qquad \qquad \qquad\) C.①正确 , ②错误 \(\qquad \qquad \qquad \qquad\) D.①都错误 , ②正确
参考答案
1.\(ABC\)
2.\(B\)
3.\(BCD\)
4.\(x^2=\dfrac{16}{5}y\)
5.\(A\)
【题型三】最值问题
【典题1】如图所示点\(F\)是抛物线\(y^2=8x\)的焦点 , 点\(A、B\)分别在抛物线\(y^2=8x\)及圆\((x-2)^2+y^2=16\)的实线部分上运动 , 且\(AB\)总是平行于\(x\)轴 , 则\(△FAB\)的周长的取值范围是\(\underline{\quad \quad}\) .

【解析】抛物线的准线\(l:x=-2\), 焦点\(F(2 ,0)\),
由抛物线定义可得\(|AF|=x_A+2\),
圆\((x-2)^2+y^2=16\)的圆心为\((2 ,0)\), 半径为\(4\),
\(∴△FAB\)的周长\(=|AF|+|AB|+|BF|=x_A+2+(x_B-x_A )+4=6+x_B\),
由抛物线\(y^2=8x\)及圆\((x-2)^2+y^2=16\)得交点的横坐标为\(2\),
\(∴x_B∈(2 ,6) ,∴6+x_B∈(8 ,12)\)
【点拨】\(△FAB\)的周长是由点\(B\)确定的,结合抛物线的定义利用几何法把\(△FAB\)周长用\(x_B\)表示 , 求出\(x_B\)的范围便可!
【典题2】已知\(O\)是坐标原点 ,\(A ,B\)是抛物线\(y=x^2\)上不同于\(O\)的两点 , 且\(OA⊥OB\), 下列结论中正确的是( )
A.\(|OA|\cdot|OB|≥2\)
B.\(.|OA|+|OB|≥2\sqrt2\)
C.直线\(AB\)过抛物线\(y=x^2\)的焦点
D.\(O\)到直线\(AB\)的距离小于或等于\(1\)
【解析】设\(A(x_1 ,x_1^2) ,B(x_2 ,x_2^2) ,(x_1≠0 ,x_2≠0 )\)
\(∵OA⊥OB\), \(∴\overrightarrow{OA}⋅\overrightarrow{OB}=0\),
\(∴\overrightarrow{OA}⋅\overrightarrow{OB}=(x_1 ,x_1^2) \cdot (x_2 ,x_2^2)\)\(=x_1 x_2+x_1^2 x_2^2=x_1 x_2 (1+x_1 x_2)=0\),
\(∴1+x_1 x_2=0\),\(∴x_2=-\dfrac{1}{x_1}\),
\(∴|OA|\cdot|OB|
=\sqrt{(x_1^2+x_1^4)⋅(x_2^2+x_2^4)}
=\sqrt{(x_1^2+x_1^4 )(\dfrac{1}{x_1^2} +\dfrac{1}{x_1^4}) }\)
\(=\sqrt{1+x_1^2+\dfrac{1}{x_1^2} +1}
≥\sqrt{2+2\sqrt{x_1^2⋅\dfrac{1}{x_1^2}}} =2\),
当且仅当\(x_1^2=\dfrac{1}{x_1^2}\) , 即\(x_1=±1\)时等号成立 , 故选项\(A\)正确 ,
又\(|OA|+|OB|≥2\sqrt{|OA|⋅|OB|}≥2\sqrt2\) , 故选项\(B\)正确 ,
\(∵\)直线AB的斜率为\(\dfrac{x_2^2-x_1^2}{x_2-x_1}=x_2+x_1=x_1-\dfrac{1}{x_1}\) ,
\(∴\)直线AB的方程为:\(y-x_1^2=(x_1-\dfrac{1}{x_1 })(x-x_1)⇒ (x_1-\dfrac{1}{x_1 })x-y+1=0\),
当\(x=0\)时 ,\(y=1\), 焦点坐标\((0 ,\dfrac{1}{4})\)不满足直线AB的方程 , 故选项\(C\)错误 ,
原点\((0 ,0)\)到直线\(AB:(x_1-\dfrac{1}{x_1 })x-y+1=0\)的距离\(d=\dfrac{1}{\sqrt{(x_1-\dfrac{1}{x_1 })^2+1^2}}≤1\), 故选项D正确 ,
故选:\(ABD\).
【点拨】
① 题中垂直关系相当了向量数量积为\(0\),\(OA⊥OB⇒\overrightarrow{OA} ⋅\overrightarrow{OB}=0\),向量进而用坐标表示;
② 本题求最值用了基本不等式\(a+b≥2\sqrt{ab}(a>0 ,b>0)\).
【典题3】若点\(P\)是曲线\(C_1:y^2=16x\)上的动点 , 点\(Q\)是曲线\(C_2:(x-4)^2+y^2=9\)上的动点 , 点\(O\)为坐标原点 , 则\(\dfrac{PQ}{OP}\)的最小值是\(\underline{\quad \quad}\) .
【解析】

设\(P\)的坐标\((x ,y)\), 由抛物线的方程\(y^2=16x\),
可得焦点\(F(4 ,0)\), 恰好为圆:\((x-4)^2+y^2=9\)的圆心 ,
因为\(P\)在抛物线上 , 所以\(|OP|=\sqrt{x^2+y^2}=\sqrt{x^2+16x}\),
\(|PQ|\)的最小值为\(P\)到圆心的距离减半径\(3\),
即\(P\)到准线的距离减\(3\)(\(P、Q、F\)三点共线时取到) ,
所以\(|PQ|=x+4-3=x+1\),
所以\(|\dfrac{PQ}{OP} |=\dfrac{x+1}{\sqrt{x^2+16x}}\),
设\(t=x+1\), 则\(x=t-1\),
所以\(|\dfrac{PQ}{OP} |=\sqrt{\dfrac{t^2}{(t-1)^2+16(t-1)}}=\sqrt{\dfrac{t^2}{t^2+14t-15}}\)
\(= \sqrt { \dfrac { 1 } { - \dfrac { 15 } { t ^ { 2 } } + \dfrac { 1 4} { t } + 1 } } = \sqrt { \dfrac { 1 } { - 15 ( \dfrac { 1 } { t } - \dfrac { 7 } { 15 } ) ^ { 2 } + \dfrac { 64 } { 15 } } }\),
当\(t=\dfrac{15}{7}\), 即\(x=\dfrac{8}{7}\)时 ,\(|\dfrac{PQ}{OP} |\)最小 , 且为\(\dfrac { \sqrt { 15 } } { 8 }\),
所以\(|\dfrac{PQ}{OP} |\)的最小值为\(\dfrac { \sqrt { 15 } } { 8 }\).
故答案为:\(\dfrac { \sqrt { 15 } } { 8 }\).
【点拨】
求\(|\dfrac{PQ}{OP} |\)的最小值,而它是由两个动点\(P、Q\)决定的,分两步走,
(1) 可先假设点\(P\)是定点,思考点\(Q\)在哪里\(|\dfrac{PQ}{OP} |\)取到最小值(此时两动点问题变成了一动点问题),而\(P\)是定点,\(OP\)是确定的,由抛物线定义可知\(|PQ|_{min}=x+1\),此时\(|\dfrac{PQ}{OP} |=\dfrac{x+1}{\sqrt{x^2+16x}}\);
(2) 接着再思考点P在哪里\(|\dfrac{PQ}{OP} |\)取到最小值,即思考\(x\)为何值时,\(\dfrac{x+1}{\sqrt{x^2+16x}}\)取到最小值?用函数方法处理便可!
巩固练习
1(★★) 已知点\(Q(2\sqrt2 ,0)\)及抛物线\(y=\dfrac{x^2}{4}\)上一动点\(P(x_0 ,y_0)\), 则\(y_0+|PQ|\)的最小值为\(\underline{\quad \quad}\) .
2(★★) 若点\(A\)为抛物线\(y^2=4x\)上一点 ,\(F\)是抛物线的焦点 ,\(|AF|=6\), 点\(P\)为直线\(x=-1\)上的动点 , 则\(|PA|+|PF|\)的最小值为\(\underline{\quad \quad}\) .
3(★★★)已知抛物线\(C:y^2=4x\)的焦点为\(F\),\(M(x_1 ,y_1) ,N(x_2 ,y_2)\)是抛物线\(C\)上的两个动点 , 若\(x_1+x_2+2=2|MN|\), 则\(∠MFN\)的最大值为\(\underline{\quad \quad}\) .
4(★★★)已知点\(M(2 ,0)\), 点\(P\)在曲线\(y^2=4x\)上运动 , 点\(F\)为抛物线的焦点 , 则\(\dfrac { | P M | ^ { 2 } } { | P F | - 1 }\)的最小值为\(\underline{\quad \quad}\) .
5(★★★) 已知抛物线\(C\)方程为\(x^2=4y\),\(F\)为其焦点 , 过点\(F\)的直线\(l\)与抛物线\(C\)交于\(A ,B\)两点 , 且抛物线在\(A ,B\)两点处的切线分别交\(x\)轴于\(P ,Q\)两点 , 则\(|AP|\cdot|BQ|\)的取值范围为\(\underline{\quad \quad}\) .
6(★★★) 已知点\(P\)是抛物线\(y^2=4x\)上动点 ,\(F\)是抛物线的焦点 , 点\(A\)的坐标为\((-1 ,0)\), 则\(\dfrac{PF}{PA}\)的最小值为\(\underline{\quad \quad}\) .
参考答案
- \(2\)
- \(2\sqrt{21}\)
- \(\dfrac{\pi}{3}\)
- \(4\)
- \([2 ,+∞)\)
- \(\dfrac{\sqrt2}{2}\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号