3.2 双曲线
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学上学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
选择性必修第一册同步提高,难度3颗星!
模块导图
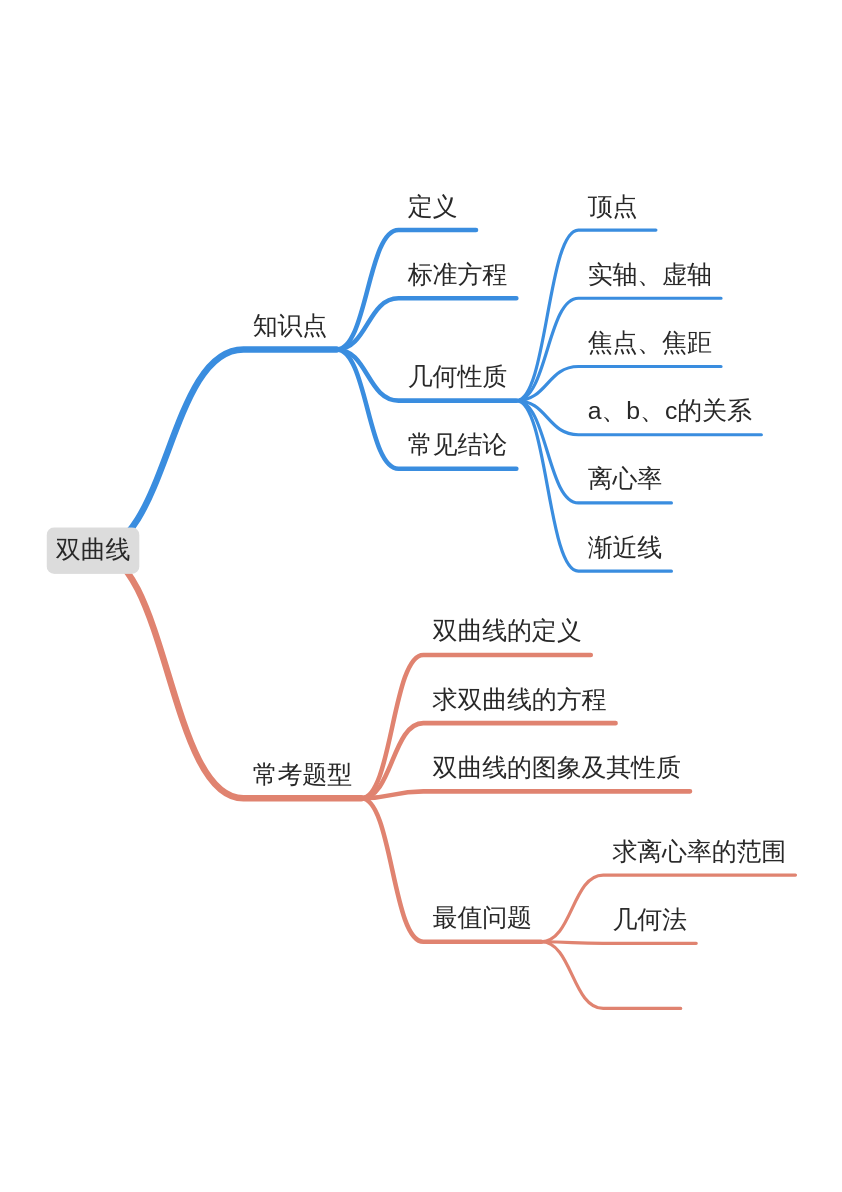
知识剖析
定义
平面内与两个定点\(F_{1},F_{2}\),的距离之差的绝对值等于常数(小于\(F_{1}F_{2}\))的点的轨迹称为双曲线.这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.
如图,\(P\)是双曲线上一点,\(| P F _ { 1 } - P F _ { 2 } | = 2 a \lt F _ { 1 } F _ { 2 }\).
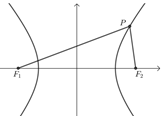
\({\color{Red}{解释}}\)
当\(PF_1-PF_2=2a<F_1 F_2\)时,轨迹仅表示双曲线的右支;
当\(PF_2-PF_1=2a<F_1 F_2\)时,轨迹仅表示双曲线的左支;
当\(|PF_1-PF_2 |=2a=F_1 F_2\)时,轨迹是一直线上以\(F_1,F_2\)为端点向外的两条射线;
当\(|PF_1-PF_2 |=2a>F_1 F_2\)时,轨迹不存在.
几何性质
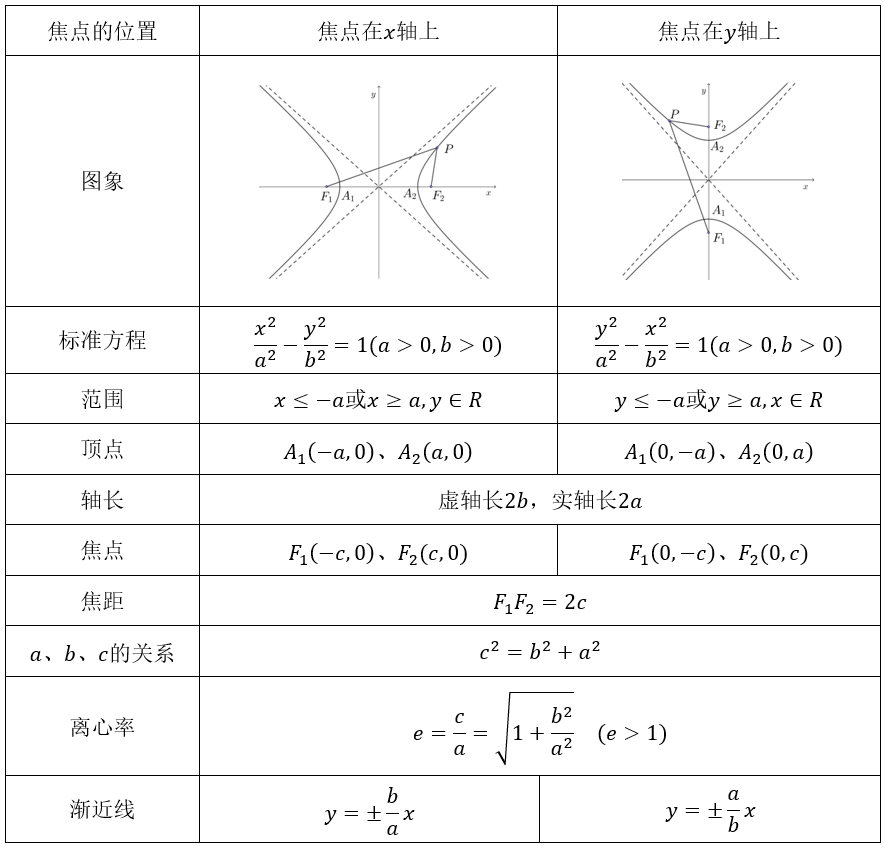
实轴和虚轴等长的双曲线称为等轴双曲线.
一些常用结论
①通径:过焦点且垂直实轴的弦,其长度为\(A B = \dfrac { 2 b ^ { 2 } } { a }\);
②焦点到渐近线的距离是\(b\);
③焦点三角形面积\(S = \dfrac { b ^ { 2 } } { \tan \frac {\angle P } { 2 } }\);
④与双曲线\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1\)共渐近线的双曲线系方程是\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = \lambda(\lambda \neq 0 )\)
⑤焦半径\(|PF_1 |=ex_P+a,|PF_2 |=ex_P-a\)(点\(P\)在双曲线右支上)
⑥双曲线\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1\)的参数方程\(\begin{cases} { x = \dfrac { a } { \cos \theta } } \\ { y = b \cdot \tan \theta } \end{cases} ( \theta 为参数 )\).
经典例题
【题型一】双曲线的定义
【典题1】平面内有两个定点\(F_1(-5,0)\)和\(F_2(5,0)\),动点\(P\)满足条件\(P F _ { 1 } - P F _ { 2 } = 6\),则动点\(P\)的轨迹是( )
A.椭圆 \(\qquad \qquad \qquad \qquad\) B.双曲线 \(\qquad \qquad \qquad \qquad\) C.双曲线的右支 \(\qquad \qquad \qquad \qquad\) D.双曲线的左支
【解析】由\(P F _ { 1 } - P F _ { 2 } = 6 <F_1F_2\)知,点\(P\)的轨迹是以\(F_1,F_2\)为焦点的双曲线右支,故选:\(C\).
【点拨】
①注意双曲线的定义中“绝对值”三字;
②若点\(P\)在右支,肯定\(P F _ { 1 } - P F _ { 2 } >0\);若点\(P\)在左支,肯定\(P F _ { 1 } - P F _ { 2 } <0\);
故题中的条件改为\(P F _ { 1 } - P F _ { 2 } = 6\),则是双曲线左支;改为\(|P F _ { 1 } - P F _ { 2 }| = 6\),则是双曲线.
【典题2】一动圆\(P\)过定点\(M(-4,0)\),且与已知圆\(N : ( x - 4 ) ^ { 2 } + y ^ { 2 } = 16\)相切,求动圆圆心\(P\)的轨迹方程.
【解析】
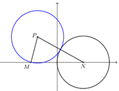
动圆圆心为\(P\),半径为\(r\),已知圆圆心为\(N\),半径为\(4\);
由题意知\(P M = r , \quad P N = r + 4\),所以\(| P N - P M | = 4\),
即动点\(P\)到两定点的距离之差为常数\(4\),
\(P\)在以为\(M,C\)焦点的双曲线上,且\(2a=4,2c=8\),
所以\(b=2\sqrt3\),
所以动圆圆心\(M\)的轨迹方程为\(\dfrac { x ^ { 2 } } { 4 } - \dfrac { y ^ { 2 } } { 12 } = 1\).
【点拨】
①两圆\(O_1,O_2\)的半径分别为\(r _ { 1 } , r _ { 2 } ( r _ { 2 } \gt r _ { 1 } )\),若两圆外切,则\(O _ { 1 } O_ { 2 } = r _ { 2 } + r _ { 1 }\);若两圆外切,则\(O _ { 1 } O _ { 2 } = r _ { 2 } - r _ { 1 } ( r _ { 2 } \gt r _ { 1 } )\);
②双曲线定义中的“常数”为\(2a\),定点为焦点.
巩固练习
1(★) 平面内到两定点\(F _ { 1 } ( - 3 , 0 ) , F _ { 2 } ( 3 , 0 )\)的距离之差的绝对值等于\(4\)的点\(M\)的轨迹( )
A.椭圆 \(\qquad \qquad \qquad \qquad\) B.线段 \(\qquad \qquad \qquad \qquad\) C.两条射线 \(\qquad \qquad \qquad \qquad\) D.双曲线
2(★★)点\(P\)到图形\(C\)上每一个点的距离的最小值称为点\(P\)到图形\(C\)的距离,那么平面内到定圆\(C\)的距离与到定点\(A\)的距离相等的点的轨迹不可能是( )
A.圆 \(\qquad \qquad \qquad \qquad\) B.椭圆 \(\qquad \qquad \qquad \qquad\) C.双曲线的一支 \(\qquad \qquad \qquad \qquad\) D.直线
参考答案
- \(D\)
- \(D\)
【题型二】 双曲线方程
【典题1】已知方程\(\dfrac { x ^ { 2 } } { 17 - k } + \dfrac { y ^ { 2 } } { k - 8 } = 1\)表示焦点在\(x\)轴上的双曲线,则\(k\)的求值范围是\(\underline{\quad \quad}\).
【解析】方程\(\dfrac { x ^ { 2 } } { 17 - k } + \dfrac { y ^ { 2 } } { k - 8 } = 1\)表示焦点在\(x\)轴上的双曲线,
可得\(17-k>0,k-8<0\),解得\(k<8\).
【点拨】
曲线方程\(C : \dfrac { x ^ { 2 } } { m } + \dfrac { y ^ { 2 } } { n } = 1\),
当\(mn<0\)时,\(C\)为双曲线;
当\(m>0,n<0\)时,\(C\)为焦点在\(x
\)轴上的双曲线且\(a^2=m\);
当\(n>0,m<0\)时,\(C\)为焦点在\(y\)轴上的双曲线且\(a^2=n\).
简而言之:双曲线,看分母正负.
【典题2】双曲线过点\(( 4 , \sqrt { 3 } ) , ( 3 , \dfrac { \sqrt { 5 } } { 2 } )\),则双曲线的标准方程为\(\underline{\quad \quad}\).
【解析】\({\color{Red}{方法一}}\) 当双曲线焦点在\(x\)轴上,设方程为\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1\),
则\(\begin{cases} { \dfrac { 16 } { a ^ { 2 } } - \dfrac { 3 } { b ^ { 2 } } = 1 } \\ { \dfrac { 9 } { a ^ { 2 } } - \dfrac { 5 } { 4 b ^ { 2 } } = 1 } \end{cases} \Rightarrow a ^ { 2 } = 4 , b ^ { 2 } = 1\),双曲线的标准方程为\(\dfrac { x ^ { 2 } } { 4 } - y ^ { 2 } = 1\).
当双曲线焦点在\(y\)轴上,设方程为\(\dfrac {y ^ { 2 } } { a ^ { 2 } } - \dfrac { x ^ { 2 } } { b ^ { 2 } } = 1\),
则\(\begin{cases} { \dfrac { 3 } { a ^ { 2 } } - \dfrac { 16 } { b ^ { 2 } } = 1 } \\ { \dfrac { 5 } { 2 a ^ { 2 } } - \dfrac { 9 } { b ^ { 2 } } = 1 } \end{cases}\)此方程组无解;
所以双曲线的标准方程为\(\dfrac { x ^ { 2 } } { 4 } - y ^ { 2 } = 1\).
\({\color{Red}{方法二}}\) 由题意,设双曲线方程为\(m x ^ { 2 } + n y ^ { 2 } = 1\),代入点\(( 4 , \sqrt { 3 } ) , ( 3 , \dfrac { \sqrt { 5 } } { 2 } )\),
得\(\begin{cases}{ 16 m + 3 n = 1 } \\ { 9 m + \dfrac { 5 } { 4 } n = 1 } \end{cases}\),解得\(m = \dfrac { 1 } { 4 } , n = - 1\).
所以双曲线的标准方程为\(\dfrac { x ^ { 2 } } { 4 } - y ^ { 2 } = 1\).
【点拨】求双曲线的方法,可用待定系数法,方法一考虑到焦点的位置作分类讨论求解,方法二则简洁些,设双曲线方程为\(m x ^ { 2 } + n y ^ { 2 } = 1\).
【典题3】与双曲线\(C:\dfrac { x ^ { 2 } } { 2 } - y ^ { 2 } = 1\)共渐近线,且经过点\(( 3 , \dfrac { \sqrt { 10 } } { 2 } )\)的双曲线标准方程是\(\underline{\quad \quad}\) .
【解析】根据题意,要求双曲线与双曲线\(C:\dfrac { x ^ { 2 } } { 2 } - y ^ { 2 } = 1\)共渐近线,
设要求的双曲线为\(\dfrac { x ^ { 2 } } { 2 } - y ^ { 2 } = t , ( t \neq 0 )\),
又由双曲线经过点\(( 3 , \dfrac { \sqrt { 10 } } { 2 } )\),
则有\(\dfrac { 9 } { 2 } - \dfrac { 10 } { 4 } = t\),解可得\(t=2\),
则要求双曲线的标准方程为\(\dfrac { x ^ { 2 } } { 4 } - \dfrac { y ^ { 2 } } { 2 } = 1\).
【点拨】
①求双曲线渐近线的一种方法,
比如求\(\dfrac { y ^ { 2 } } { 4 } - \dfrac { x ^ { 2 } } { 9 } = 1\)的渐近线,直接令\(\dfrac { y ^ { 2 } } { 4 } - \dfrac { x ^ { 2 } } { 9 } =0 \Rightarrow \dfrac { y ^ { 2 } } { 4 } = \dfrac { x ^ { 2 } } { 9 } \Rightarrow y =\pm \dfrac { 2 x } { 3 }\),
该方法不需要确定焦点位置与\(a,b\)值.
②与双曲线\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)共渐近线的方程为\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = \lambda (\lambda \neq 0 )\);
巩固练习
1(★) 若\(k\in R\),则\(k>-3\)是方程\(\dfrac { x ^ { 2 } } { k - 3 } + \dfrac { y ^ { 2 } } { k + 3 } = 1\)表示双曲线的( )
A.充分不必要条件 \(\qquad \qquad\) B.必要不充分条件 \(\qquad \qquad\) C.充要条件 \(\qquad \qquad\) D.既不充分也不必要条件
2(★★) 已知双曲线的一条渐近线方程为\(y=2x\),且经过点\(( 4 , 4 \sqrt { 3 } )\),则该双曲线的标准方程为\(\underline{\quad \quad}\).
3(★★) 在下列条件下求双曲线标准方程.
(1) 经过两点\(( 3 , 0 ) , ( - 6 , - 3 )\);
(2) \(a = 2 \sqrt { 5 }\),经过点\((2,-5)\),焦点在\(y\)轴上.
参考答案
- \(B\)
- \(\dfrac { x ^ { 2 } } { 4 } - \dfrac { y ^ { 2 } } { 16 } = 1\)
- \((1)\dfrac { x ^ { 2 } } { 9 } - \dfrac { y ^ { 2 } } { 3 } = 1 \quad ( 2 ) \dfrac { y ^ { 2 } } { 20 } - \dfrac { x ^ { 2 } } { 16 } = 1\)
【题型三】 双曲线的图像及其性质
【典题1】已知双曲线的方程为\(\dfrac { x ^ { 2 } } { 16 } - \dfrac { y ^ { 2 } } { 9 } = 1\),则下列说法错误的是( )
A.双曲线\(C\)的实轴长为\(8\)
B.双曲线\(C\)的渐近线方程为\(y = \dfrac { 3 } { 4 } x\)
C.双曲线\(C\)的焦点到渐近线的距离为\(3\)
D.双曲线\(C\)上的点到焦点距离的最小值为\(\dfrac{9}{4}\)
【解析】双曲线的方程为\(\dfrac { x ^ { 2 } } { 16 } - \dfrac { y ^ { 2 } } { 9 } = 1\),所以\(a = 4 , \quad b = 3\),
所以\(c = \sqrt { a ^ { 2 } + b ^ { 2 } } = 5\),
所以实轴长为\(2 a = 2 \times 4 = 8\),即\(A\)正确;
渐近线方程为\(y = \pm\dfrac { b } { a } x = \pm\dfrac { 3 } { 4 } x\),即正确;
焦点\(( 5 , 0 )\)到渐近线\(y = \dfrac { 3 } { 4 } x\)的距离为\(\dfrac { | \dfrac { 3 } { 4 } \times 5 | } { \sqrt { ( \dfrac { 3 } { 4 } ) ^ { 2 } + 1 } } = 3\),即\(C\)正确;
对于选项\(D\),设点\(P ( x , y )\)为双曲线右支上的一点,点\(F\)为双曲线的右焦点,
当\(x=4\)时,\(PF\)取最小值\(1\),即\(D\)错误.
故选:\(D\).
【点拨】
①焦点到渐近线的距离是\(b\);
②双曲线上的点到焦点的距离最小值是当点在顶点的位置时取到.
【典题2】设双曲线\(C:\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\),的左、右焦点分别为\(F _ { 1 } , F _ { 2 }\),离心率为\(\sqrt3\),\(P\)是\(C\)上一点,且\(\angle F _ { 1 } P F _ { 2 } = 60 ^ { \circ }\),若\(\triangle F _ { 1 } P F _ { 2 }\)的面积为\(4\sqrt3\),则\(a=\)\(\underline{\quad \quad}\) .
【解析】
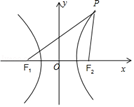
根据题意,几何关系如图所示.设\(| P F _ { 2 } | = m , \quad | P F _ { 1 } | = n\),
若\(\triangle F _ { 1 } P F _ { 2 }\)的面积为\(4\sqrt3\),可得\(\dfrac { 1 } { 2 } m n \sin 60 ^ { \circ } = 4 \sqrt { 3 }\),
由双曲线定义,可得\(n-m=2a\),
由余弦定理可得\(4 c ^ { 2 } = m ^ { 2 } + n ^ { 2 } - 2 m n \cos 60 ^ { \circ }\),
所以\(4 c ^ { 2 } = 4 a ^ { 2 } + 2 m n - m n = 4 a ^ { 2 } + m n = 4 a ^ { 2 } + 16\),
离心率为\(\sqrt3\).可得\(\dfrac { c } { a } = \sqrt { 3 }\),代入上式,可得\(a = \sqrt { 2 }\).
【点拨】
①遇到焦点三角形\(\triangle F _ { 1 } P F _ { 2 }\)时,要注意双曲线的定义与解三角形内容(正弦定理、余弦定理、面积公式等)的运用;
②在双曲线中,焦点三角形\(\triangle F _ { 1 } P F _ { 2 }\)的面积为\(S = \dfrac { b ^ { 2 } } { \tan \dfrac { \angle P } { 2 } }\),这属于二级结论,本题用上题目求解就较简洁些,\(S = \dfrac { b ^ { 2 } } { \tan \dfrac { \angle P } { 2 } } = 4 \sqrt { 3 } \Rightarrow \dfrac { b ^ { 2 } } { \tan 30 ^ { \circ } } = 4 \sqrt { 3 } \Rightarrow b = 2\),又\(\dfrac { c } { a } = \sqrt { 3 }\),易得\(a = \sqrt { 2 }\).
【典题3】已知双曲线\(C : \dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)的左、右焦点分别为\(F _ { 1 } , F _ { 2 }\),过\(F _ { 1 }\)作斜率为\(\dfrac { \sqrt { 2 } } { 2 }\)的直线\(l\)与双曲线\(C\)的左、右两支分别交于\(A,B\)两点,若\(| A F _ { 2 } | = | B F _ { 2 } |\),则双曲线的离心率为\(\underline{\quad \quad}\) .
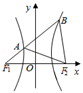
【解析】 \({\color{Red}{方法一}}\)设\(A ( x _ { 1 } , y _ { 1 } ) , B ( x _ { 2 } , y _ { 2 } )\),
依题意可设直线方程为\(y = \dfrac { \sqrt { 2 } } { 2 } ( x - c )\),
由\(\begin{cases} { y = \dfrac { \sqrt { 2 } } { 2 } ( x - c ) } \\ { \dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 } \end{cases}\),
得\(( 2 b ^ { 2 } - a ^ { 2 } ) x ^ { 2 } - 2 c a ^ { 2 } x - a ^ { 2 } c ^ { 2 } - 2 a ^ { 2 } b ^ { 2 } = 0\),
则\(x _ { 1 } + x _ { 2 } = \dfrac { 2 c a ^ { 2 } } { 2 b ^ { 2 } - a ^ { 2 } }\),
因为\(| A F _ { 2 } | = | B F _ { 2 } |\),
由两点距离公式可得\(\sqrt { ( x _ { 1 } - c ) ^ { 2 } + y _ { 1 } ^ { 2 } } = \sqrt { ( x _ { 2 } - c ) ^ { 2 } + y _ { 2 } ^ { 2 }}\),
又\(y _ { 1 } ^ { 2 } = b ^ { 2 } ( \dfrac { x _ { 1 } ^ { 2 } } { a ^ { 2 } } - 1 ) , y _ { 2 } ^ { 2 } = b ^ { 2 } ( \dfrac { x _ { 2 } ^ { 2 } } { a ^ { 2 } } - 1 )\),
化简可得\(2 a ^ { 2 } = c ( x _ { 1 } + x _ { 2 } )\),
所以\(2 a ^ { 2 } = c \cdot \dfrac { 2 c a ^ { 2 } } { 2 b ^ { 2 } - a ^ { 2 } } \Rightarrow b ^ { 2 } = 2 a ^ { 2 } \Rightarrow e = \sqrt { 1 + \dfrac { b ^ { 2 } } { a ^ { 2 } } } = \sqrt { 3 }\)
\({\color{Red}{方法二}}\) 如图,
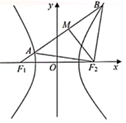
取\(AB\)中点\(M\),连结\(F _ { 2 } M\),
因为\(| A F _ { 2 } | = | B F _ { 2 } |\),所以\(F _ { 2 } M \perp A B\),
设\(| A F _ { 2 } | = | B F _ { 2 } | =x\),
因为\(| A F _ { 2 } | - | A F _ { 1 } | = 2 a\),所以\(| A F _ { 1 } | = x - 2 a\),
又\(| B F _ { 1 } | - | B F _ { 2 } | = 2 a\),所以\(| B F _ { 1 } | = x + 2 a\),
所以\(| A B | = | B F _ { 1 } | - | A F _ { 1 } | = 4 a\),所以\(| A M | = | B M | = 2 a\)所以\(| F _ { 1 } M | = | B F _ { 1 } | - | B M | = x\),
由勾股定理,知\(|F _ { 2 } M | = \sqrt { ( F _ { 1 }F _ { 2 } ) ^ { 2 } - ( M F _ { 1 } ) ^ { 2 } } = \sqrt { ( B F _ { 2 } ) ^ { 2 } - ( B M ) ^ { 2 } }\),
即\(| F _ { 2 } M | = \sqrt { 4 c ^ { 2 } - x ^ { 2 } } = \sqrt { x ^ { 2 } - 4 a ^ { 2 } }\),解得\(x ^ { 2 } = 2 a ^ { 2 } + 2 c ^ { 2 }\)所以\(| F _ { 2 } M | = \sqrt { 2 c ^ { 2 } - 2 a ^ { 2 } } = \sqrt { 2 b ^ { 2 } }\),
所以\(\tan \angle M F _ { 1 } F _ { 2 } = \dfrac { | F _ { 2 } M | } {| F _ { 1 } M | } = \dfrac { \sqrt { 2 b ^ { 2 } } } { \sqrt { 2 a ^ { 2 } + 2 c ^ { 2 } } } = \dfrac { \sqrt { 2 } } { 2 }\),
即\(\dfrac { c ^ { 2 } - a ^ { 2 } } { a ^ { 2 } + c ^ { 2 } } = \dfrac { 1 } { 2 }\),化简得\(c ^ { 2 } = 3 a ^ { 2 }\),
离心率\(e = \dfrac { c } { a } = \sqrt { 3 }\).
【点拨】
①方法一是由条件“过\(F _ { 1 }\)作斜率为\(\dfrac { \sqrt { 2 } } { 2 }\)的直线\(l\)”,想用代数法求解;代数法中\(| A F _ { 2 } | = | B F _ { 2 } |\)用两点距离公式处理了;
②方法二是通过平几的知识点求解,要多观察图形,多积累一些平几的结论与常见已知条件的处理方法:(1)\(| A F _ { 2 } | = | B F _ { 2 } | \Rightarrow\)等腰三角形的三线合一;(2)斜率为\(\dfrac { \sqrt { 2 } } { 2 }\),即\(\tan\angle F _ { 1 } = \dfrac { \sqrt { 2 } } { 2 }\),则找直角三角形\(\triangle MF_1F_2\),易得\(\dfrac { | F _ { 2 } M| } { | F_ { 2 }M|} = \dfrac { \sqrt { 2 } } { 2 }\);
③比较两种方法,在本题中计算量来看,方法二优于方法一;思考难度来看,方法一稍容易想到.
【典题4】已知\(F _ { 1 } , F _ { 2 }\)分别为双曲线\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1 ( a \gt 0 , b \gt 0 )\)的左右焦点,且\(| F _ { 1 } F _ { 2 } | = \dfrac { 2 b ^ { 2 } } { a }\),点\(P\)为双曲线右支上一点,\(I\)为\(\triangle P F _ { 1 } F _ { 2 }\)的内心,过原点\(O\)作\(PI\)的平行线交\(PF_1\)于\(K\),若\(S _ {\triangle I P F _ { 1 } } = S _ { \triangle I P F_ { 2 } } + \lambda S _ {\triangle I F _ { 1 }F_2 }\)成立,则下列结论正确的有( )
A.\(\lambda= \dfrac { \sqrt { 5 } - 1 } { 2 }\) \(\qquad \qquad\) B.\(\lambda= \dfrac { \sqrt { 5 } + 1 } { 2 }\) \(\qquad \qquad\) C.点\(I\)的横坐标为\(a\) \(\qquad \qquad\)D.\(PK=a\)
【解析】
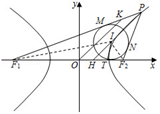
因为\(| F _ { 1 } F _ { 2 } | = \dfrac { 2 b ^ { 2 } } { a }\),所以\(2 c = \dfrac { 2 b ^ { 2 } } { a } = \dfrac { 2 c ^ { 2 } - 2 a ^ { 2 } } { a }\),
整理得\(e ^ { 2 } - e - 1 = 0\),
因为\(e>1\),所以\(e= \dfrac { \sqrt { 5 } + 1 } { 2 }\),.
设\(\triangle P F _ { 1 } F _ { 2 }\)的内切圆半径为\(r\),
由双曲线的定义得\(| P F _ { 1 } | - | P F _ { 2 } | = 2 a , | F _ { 1 } F _ { 2 } | = 2 c\),
\(S _ {\triangle I P F _ { 1 } } = \dfrac { 1 } { 2 } | P F _ { 1 } | r , S _ {\triangle IP F_ { 2 } } = \dfrac { 1 } { 2 } | P F_2| r\),\(S _ { \triangle I F_1F _2} = \dfrac { 1 } { 2 } \cdot 2 c \cdot r = c r\),
因为\(S _ {\triangle I P F_ { 1 } } = S _ { \triangle I P F_ { 2 } } + \lambda S _ {\triangle I F _ { 1 }F_2 }\),
所以\(\dfrac { 1 } { 2 } | P F _ { 1 } | \cdot r = \dfrac { 1 } { 2 } | P F _ { 2 } | \cdot r + \lambda c r\),
故\(\lambda= \dfrac { | P F _ { 1 } | - | P F _ { 2 } | } { 2 c } = \dfrac { a } { c } = \dfrac { 1 } { \dfrac { 1 + \sqrt { 5 } } { 2 } } = \dfrac { \sqrt { 5 } - 1 } { 2 }\),
所以\(A\)正确,\(B\)错误.
设内切圆与\(P F _ { 1 } , P F _ { 2 } , F _ { 1 } F _ { 2 }\)的切点分别为\(M,N,T\),
可得\(| P M | = | P N | , | F _ { 1 } M | = | F _ { 1 } T | ,| F _ { 2 } N | = | F _ { 2 } T |\),
由\(| P F _ { 1 } | - | P F _ { 2 } | = | F _ { 1 } M | - | F _ { 2 } N | = | F _ { 1 } T | - | F _ { 2 } T | = 2 a\),\(| F _ { 1 } F _ { 2 } | = | F _ { 1 } T | + | F _ { 2 } T | = 2 c\),
可得\(| F _ { 2 } T | = c - a\),可得\(T\)的坐标为\((a,0)\),
即点\(I\)的横坐标为\(a\) ,故\(C\)正确;
设\(PI\)延长线与\(F _ { 1 } F _ { 2 }\)交于\(H\),可得\(\dfrac { | P F _ { 2 } | } { | P F _ { 1 } | } = \dfrac { | F _ { 2 } H | } { | F _ { 1 }H | }\),
由\(| P F _ { 1 } | - | P F _ { 2 } | = 2 a\),
可得\(\dfrac { 2 a } { | P F _ { 1 } | } = \dfrac { 2 | O H | } { | F _ { 1 } H | }\),①
由三角形的相似的性质可得\(\dfrac { | P K | } { | O H | } = \dfrac { | P F _ { 1 } | } { | H F _ { 1 } | }\),②
由①②可得\(| P K | = a\).故\(D\)正确.
故选:\(ACD\).
【点拨】
①得到\(a,b,c\)任意两个量或三量的一条等式,均可得到关于离心率\(e\)的方程从而求出.
②注意内心的定义及其性质,内心是三角形的角平分线交点,则内心到三边的距离相等!
③角平分线定理:如图,在\(\triangle A B C\)中,\(AD\)是\(\angle BAC\)的角平分线,则\(\dfrac { A B } { B D } = \dfrac { A C } { C D }\).
④多观察图形,充分利用平几的知识点,得到各角之间或各线段之间的关系.常见的相似三角形的性质(注意\(A\)字型、\(8\)字型模型)、等腰三角形的三线合一、角平分线、圆的性质、正余弦定理等等.
巩固练习
1(★) 若双曲线\(C:mx^2-y^2=2\)的实轴长等于虚轴长的一半,则\(m=\)( )
A.\(\dfrac{1}{4}\) \(\qquad \qquad \qquad \qquad\)B.\(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\) C.\(4\) \(\qquad \qquad \qquad \qquad\) D.\(2\)
2 (★★)[多选题] 已知双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的离心率为\(\dfrac{2\sqrt3}{3}\),右顶点为\(A\),以\(A\)为圆心,\(b\)为半径作圆\(A\),圆\(A\)与双曲线\(C\)的一条渐近线交于\(M、N\)两点,则有 ( )
A.渐近线方程为\(y=±\sqrt3 x\) \(\qquad\)B.渐近线方程为\(y=±\dfrac{\sqrt3}{3} x\) \(\qquad\)C.\(∠MAN=60^°\) \(\qquad\)D.\(∠MAN=120^°\)
3(★★)[多选题] 已知\(F_1,F_2\)分别是双曲线\(\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左、右焦点,\(A\)为左顶点,\(P\)为双曲线右支上一点,若\(|PF_1 |=2|PF_2 |\)且\(△PF_1 F_2\)的最小内角为\(30^°\),则( )
A.双曲线的离心率\(\sqrt3\)
B.双曲线的渐近线方程为\(y=±\sqrt2x\)
C.\(∠PAF_2=45^°\)
D.直线\(x+2y-2=0\)与双曲线有两个公共点
4(★★) 已知点\(F_1 (-3,0),F_2 (3,0)\)分别是双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左、右焦点,\(M\)是\(C\)右支上的一点,\(MF_1\)与\(y\)轴交于点\(P\),\(△MPF_2\)的内切圆在边\(PF_2\)上的切点为\(Q\),若\(|PQ|=2\),则\(C\)的离心率为\(\underline{\quad \quad}\).
5(★★★)已知双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左、右焦点分别为\(F_1,F_2\),过\(F_1\)的直线与\(C\)的左、右支分别交于\(P、Q\)两点,\(\overrightarrow{PQ}=2\overrightarrow{F_1 P} ,\overrightarrow{F_1 Q} \cdot \overrightarrow{F_2 Q} =0\),则\(C\)的渐近线方程为\(\underline{\quad \quad}\) .
6(★★★) 如图所示,已知双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的右焦点为\(F\),双曲线\(C\)的右支上一点\(A\),它关于原点\(O\)的对称点为\(B\),满足\(∠AFB=120^°\),且\(|BF|=2|AF|\),则双曲线\(C\)的离心率是\(\underline{\quad \quad}\) .
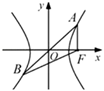
7(★★★)已知双曲线\(\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左、右焦点分别\(F_1,F_2\),过\(F_2\)的直线交双曲线右支于\(A,B\)两点.\(∠F_1 AF_2\)的平分线交\(BF_1\)于\(D\),若\(\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AF_1} +\overrightarrow{AF_2}\),则双曲线的离心率为\(\underline{\quad \quad}\).
8(★★★) 已知双曲线\(\dfrac { x ^ { 2 } } { 4 } - \dfrac { y ^ { 2 } } { 3 } = 1\)的左、右焦点分别为\(F_1,F_2\),\(O\)为双曲线的中心,\(P\)是双曲线右支上的点,\(△PF_1 F_2\)的内切圆的圆心为\(I\),且圆\(I\)与\(x\)轴相切于点\(A\),过\(F_2\)作直线\(PI\)的垂线,垂足为\(B\),则\(\dfrac { | OB | } { | O A | } =\) \(\underline{\quad \quad}\).
参考答案
- \(C\)
- \(BC\)
- \(ABD\)
- \(\dfrac {3}{2}\)
- \(y=±2x\)
- \(\sqrt3\)
- \(\sqrt3\)
- \(1\)
【题型四】最值问题
情况1 求离心率范围
【典题1】已知双曲线\(\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)在两条渐近线所构成的角中,设以实轴为角平分线的角为\(\theta\),若\(\theta\)的取值范围是\([ \dfrac { \pi } { 2 } , \dfrac { 2 \pi } { 3 } ]\),则该双曲线离心率的取值范围是( )
A.\(( 1 , \sqrt { 2 } ]\) \(\qquad \qquad \qquad \qquad\) B.\([ \sqrt { 2 } , 2 ]\) \(\qquad \qquad \qquad \qquad\) C.\([ \dfrac { 2 \sqrt { 3 } } { 3 } , \sqrt { 2 } ]\) \(\qquad \qquad \qquad \qquad\) D.\([ 2 , + \infty )\)
【解析】根据题意,易得双曲线的实轴长为\(2a\),虚轴长为\(2b\);
由双曲线的意义,可得\(e ^ { 2 } = \dfrac { c ^ { 2 } } { a ^ { 2 } } = 1 + \dfrac { b ^ { 2 } } { a ^ { 2 } }\),
以实轴为角平分线的角为\(\theta\),若\(\theta\)的取值范围是\([ \dfrac { \pi } { 2 } , \dfrac { 2 \pi } { 3 } ]\),
可得\(1 \leq \dfrac { b } { a } \leq \sqrt { 3 }\);
进而可得:\(e ^ { 2 } = 1 + \dfrac { b ^ { 2 } } { a ^ { 2 } }\in [ 2 , 4 ]\),所以\(e \in [ \sqrt { 2 } , 2 ]\).故选:\(B\).
【点拨】
求离心率的范围的一般思路:求出\(a,b,c\)任意两个量比值的范围得到关于离心率\(e\)的不等式,从而求出\(e\)的范围,同时也要注意椭圆中\(0 \lt e \lt 1\),双曲线中\(e>1\).
情况2 几何法求范围
【典题1】已知双曲线\(x ^ { 2 } - y ^ { 2 } = 1\)的右焦点为\(F\),右顶点\(A\),\(P\)为渐近线上一点,则\(| P A | + | P F |\)的最小值为( )
A.\(2\sqrt3\) \(\qquad \qquad \qquad \qquad\) B. \(\sqrt3\) \(\qquad \qquad \qquad \qquad\) C.\(2\) \(\qquad \qquad \qquad \qquad\)D.\(\sqrt5\)
【解析】
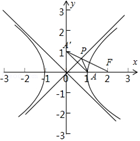
如图:双曲线\(x ^ { 2 } - y ^ { 2 } = 1\)的右焦点为\(F ( \sqrt { 2 } , 0 )\),
右顶点\(A(1,0)\),\(P\)为渐近线\(y=x\)上一点,
则\(| P A | + | P F |\)的最小值就是\(A\)关于\(y=x\)的对称点\(A ^ { \prime }\)到的距离,
所以\(A ^ { \prime }(0,1)\),
则\(| P A | + | P F |\)的最小值为:\(\sqrt { ( \sqrt { 2 } ) ^ { 2 } + 1 ^ { 2 } } = \sqrt { 3 }\).
故选:\(B\).
【点拨】这属于“将军饮马问题”!
【典题2】 点\(F_2\)是双曲线\(C:\dfrac { x ^ { 2 } } { 9 } - \dfrac { y ^ { 2 } } { 3 } = 1\)的右焦点,动点\(A\)在双曲线左支上,直线\(l _ { 1 } : t x - y + t - 2 = 0\)与直线\(l _ { 2 } : x + t y + 2 t - 1 = 0\)的交点为\(B\),则\(| A B | + | A F _ { 2 } |\)的最小值为( )
A.\(8\) \(\qquad \qquad \qquad \qquad\) B. \(5 \sqrt { 3 }\) \(\qquad \qquad \qquad \qquad\) C.\(9\) \(\qquad \qquad \qquad \qquad\) D.\(6\sqrt { 3 }\)
【解析】联立直线\(l _ { 1 } , l _ { 2 }\)的方程\(\begin{cases} { t x - y + t - 2 = 0 } \\ { x + t y + 2 t - 1 = 0 } \end{cases}\),
可得\(\begin{cases} { x = - \dfrac { t ^ { 2 } - 1 } { t ^ { 2 } + 1 } } \\ { y + 2 = \dfrac { 2 t } { t + 1 } } \end{cases}\),消参数\(t\)可得\(x ^ { 2 } + ( y + 2 ) ^ { 2 } = 1\),
所以可得交点\(B\)的轨迹为圆心在\((0,-2)\),半径为\(1\)的圆,
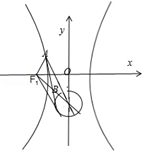
由双曲线的方程可得\(a = 3 , b = \sqrt { 3 }\),焦点\(F ( - 2 \sqrt { 3 } , 0 )\),
可得\(| A F _ { 2 } | = | A F _ { 1 } | + 2 a = | A F _ { 1 } | + 6\),
所以\(| A B | + | A F _ { 2 } | = | A B | + | A F _ { 1 } | + 6\),
当\(A , F _ { 1 } , B\)三点共线时,\(| A B | + | A F _ { 2 } |\)最小,
所以\(| A B | + | A F_2 | = | A B | + | A F _ { 1 } | + 6 \geq | B F _ { 1 } | - 1 + 6 = \sqrt { ( - 2 \sqrt { 3 } ) ^ { 2 } + 2 ^ { 2 } } + 5 = 9\),
当过\(F_1\)与圆心的直线与圆的交点\(B\)且在\(F_1\)和圆心之间时最小.
所以\(| A B | + | A F _ { 2 } |\)的最小值为\(9\),故选:\(C\).
【点拨】这属于“三点共线取最值”模型,在圆锥曲线求最值问题用几何法需要明确动点的运动规律,平时掌握常见模型,多观察图象.
情况3 函数法求范围
【典题1】[多选题]已知为双曲线\(C:\dfrac { x ^ { 2 } } { 3 } - y ^ { 2 } = 1\)上的动点,过\(P\)作两渐近线的垂线,垂足分别为\(A,B\),记线段\(PA,PB\)的长分别为\(m,n\),则( )
A.若\(PA,PB\)的斜率分别为\(k _ { 1 } , k _ { 2 }\),则$ k _ { 1 } \cdot k _ { 2 } = - 3$
B.\(m n = \dfrac { 1 } { 2 }\)
C.\(4m+n\)的最小值为 \(\sqrt3\)
D.\(AB\)的最小值为\(\dfrac { 1 } { 2 }\)
【解析】
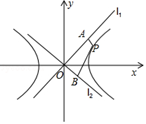
如图所示,设\(P ( x _ { 0 } , y _ { 0 } )\),则\(\dfrac { x_0 ^ { 2 } } { 3 } - y _ { 0 } ^ { 2 } = 1\).
由题设条件知,双曲线的两渐近线:
\(l _ { 1 } : y = \dfrac { \sqrt { 3 } } { 3 } x , l _ { 2 } : y = - \dfrac { \sqrt { 3 } } { 3 } x\).
设直线\(PA,PB\)的斜率分别为\(k _ { 1 } , k _ { 2 }\),
则\(k _ { 1 } = - \sqrt { 3 } , \quad k _ { 2 } = \sqrt { 3 }\),
所以\(k _ { 1 } \cdot k _ { 2 } = - 3\) ,故选项\(A\)正确;
由点线距离公式知:\(| P A | = m = \dfrac { | \sqrt { 3 } x _ { 0 } - 3 y _ { 0 } | } { 2 \sqrt { 3 } } , | P B | = n = \dfrac { | \sqrt { 3 } x _ { 0 } + 3 y _ { 0 } | } { 2 \sqrt { 3 } }\),
所以\(m n = \dfrac { | 3 x _ { 0 } ^ { 2 } - 9 y _ { 0 } ^ { 2 } | } { 12 } = \dfrac { 9 } { 12 } \times | \dfrac { x _ { 0 } ^ { 2 } } { 3 } - y _ { 0 } ^ { 2 } | = \dfrac { 3 } { 4 }\) ,
故选项\(B\)错误;
因为\(4 m + n \geq 4 \sqrt { m m } = 4 \times \dfrac { \sqrt { 3 } } { 2 } = 2 \sqrt { 3 }\),所以\(C\)不正确;
由渐近线的斜率可知\(\angle AOx = 30 ^ { \circ }\),所以\(\angle AOB =60 ^ { \circ }\),
四边形\(AOBP\)中易得\(\angle APB = 120 ^ { \circ }\),
所以\(| A B | = \sqrt { P A ^ { 2 } + P B ^ { 2 } - 2 P A \cdot P B \cdot \cos \angle A P B }=\sqrt { m ^ { 2 } + n ^ { 2 } + m n } \geq \sqrt { 3 m n } = \dfrac { 3 } { 2 }\),
(当\(m=n\),即点\(P\)在双曲线的顶点位置时)
所以\(D\)正确,
故选:\(AD\).
【点拨】
①\(PA,PB\)两条线段长度由点\(P\)确定,根据题意用点到直线的距离公式表示出来;
②求\(4m+n\)与\(AB=\sqrt { m ^ { 2 } + n ^ { 2 } + m n }\)时,用基本不等式\(a + b \geq 2 \sqrt { a b } ( a \gt 0 , b \gt 0 )\)求最值.
③思考:如何处理含一个变量与两个变量的式子最值问题呢?
(1) 含一个变量的,比如求\(\dfrac { 1 } { m } - \dfrac { 4 } { 4 + m } ( m \geq 1 )\)的最小值,想到构造\(f ( m ) = \dfrac { 1 } { m } - \dfrac { 4 } { 4 + m } ( m \geq 1 )\),再用函数最值方法求解;
(2) 含两个变量,比如本题中\(AB=\sqrt { m ^ { 2 } + n ^ { 2 } + m n }\),在高中阶段常用基本不等式处理,那转化为只含一个变量?思路有两条,一是用\(n\)表示\(m\)消掉一个变量,但本题\(m,n\)没明显的关系;二是用另外一个变量表示,这是可以的,用双曲线的参数方程设点\(P ( \dfrac { \sqrt { 3 } } { \cos \alpha } , \tan \alpha )\),就可以用\(\alpha\)表示\(m,n\),从而\(\sqrt { m ^ { 2 } + n ^ { 2 } + m n }\)变成一个变量表示\(\alpha\),但计算量较大.
【典题2】已知双曲线\(\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的一条渐近线方程为\(y = \dfrac { \sqrt { 3 } } { 2 } x\),\(P\)为双曲线上一个动点,\(F _ { 1 } , F _ { 2 }\)为其左,右焦点,\(\overrightarrow{PF_1}\cdot \overrightarrow{PF_2}\)的最小值为\(-3\),则此双曲线的焦距为( )
A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(4\) \(\qquad \qquad \qquad \qquad\) C.\(2\sqrt5\) \(\qquad \qquad \qquad \qquad\) D.\(2\sqrt7\)
【解析】因为双曲线\(\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的一条渐近线方程为\(y = \dfrac { \sqrt { 3 } } { 2 } x\),所以\(\dfrac { b } { a } = \dfrac { \sqrt { 3 } } { 2 }\),
不妨设\(a = 2 k , \quad b = \sqrt { 3 } k , \quad k \gt 0\),
所以\(c = \sqrt { a ^ { 2 } + b ^ { 2 } } = \sqrt { 7 k }\),
所以\(F _ { 1 } ( - \sqrt { 7 } k , 0 ) , F _ { 2 } ( \sqrt { 7 } k , 0 )\),
设\(P ( x _ { 0 } , y _ { 0 } )\),且\(x _ { 0 } \leq - 2 k\)或\(x _ { 0 } \geq 2 k\),即\(x _ { 0 } ^ { 2 } \geq 4 k ^ { 2 }\),
因为\(\dfrac { x _ { 0 } ^ { 2 } } { a ^ { 2 } } - \dfrac { y _ { 0 } ^ { 2 } } { b ^ { 2 } } = 1\),所以\(y _ { 0 } ^ { 2 } = \dfrac { 3 } { 4 } x _ { 0 } ^ { 2 } - 3 k ^ { 2 }\),
所以\(\overrightarrow{PF _ { 1 }} \cdot \overrightarrow{P F _ { 2 } } = ( - \sqrt { 7 } k - x _ { 0 } , - y _ { 0 } ) ( \sqrt { 7 } k - x _ { 0 } , - y _ { 0 } )\)
\(= x _ { 0 } ^ { 2 } - 7 k ^ { 2 } + y _ { 0 } ^ { 2 } = \dfrac { 7 } { 4 } x _ { 0 } ^ { 2 } - 1 0k^2\)
\(\geq 7 k ^ { 2 } - 10 k ^ { 2 } = - 3 k ^ { 2 } = - 3\),
解得\(k = 1 , k = - 1\)(舍去),
所以\(c = \sqrt { 7 }\),所以\(2 c = 2\sqrt { 7 }\),
故选:\(D\).
【点拨】
①本题处理数量积的方法是坐标法,设点\(P ( x _ { 0 } , y _ { 0 } )\),得\(\overrightarrow{PF _ { 1 }} \cdot \overrightarrow{P F _ { 2 } }= x _ { 0 } ^ { 2 } - 7 k ^ { 2 } + y _ { 0 } ^ { 2 }\);
②做到\(\overrightarrow{PF _ { 1 }} \cdot \overrightarrow{P F _ { 2 } }= x _ { 0 } ^ { 2 } - 7 k ^ { 2 } + y _ { 0 } ^ { 2 }\),其中\(k\)为参数,\(x _ { 0 } , y _ { 0 }\)为变量,而点\(P\)在双曲线上,满足\(\dfrac { x ^ { 2 } } { a ^ { 2 } } - \dfrac { y ^ { 2 } } { b ^ { 2 } } = 1\),故可消元得到\(\overrightarrow{PF _ { 1 }} \cdot \overrightarrow{P F _ { 2 } }= \dfrac { 7 } { 4 } x _ { 0 } ^ { 2 } - 1 0k^2\),此时用函数方法求最小值,要注意自变量\(x_0\)的取值范围;
③利用函数法求最值,一定要谨记“优先考虑定义域”!
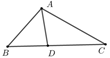
【典题3】如图,在\(\triangle ABC\)中,已知\(\angle B A C = 120 ^ { \circ }\),其内切圆与\(AC\)边相切于点\(D\),延长到\(BA\),使\(BE=BC\),连接\(CE\),设以\(E,C\)为焦点且经过点\(A\)的椭圆的离心率为\(e_1\),以\(E,C\)为焦点且经过点\(A\)的双曲线的离心率为\(e_2\),则当\(\dfrac { 2 } { e _ { 1 } } + \dfrac { 1 } { e_ 2 }\)取最大值时,\(\dfrac { A D } { D C }\)的值为\(\underline{\quad \quad}\).
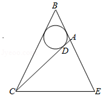
【解析】
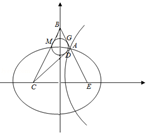
如图,设\(M,G\)分别是\(BC,BE\)与圆的切点.
由圆的切线性质,
可设\(A G = A D = 1 , \quad C D = C M = G E = m , \quad ( m \gt 1 )\),
在\(\triangle AEC\)中,
\(C E ^ { 2 } = C A ^ { 2 } + A E ^ { 2 } - 2 C A \cdot E A \cos 60 ^ { \circ } =m ^ { 2 } + 3\)
所以\(C E = \sqrt { m ^ { 2 } + 3 }\),
所以\(e _ { 1 } = \dfrac { \sqrt { m ^ { 2 } + 3 } } { 2 m }\),\(e _ { 2 } = \dfrac { \sqrt { m ^ { 2 } + 3 } } { 2 }\),
则\(\dfrac { 2 } { e _ { 1 } } + \dfrac { 1 } { e _ { 2 } } = \dfrac { 4 m + 2 } { \sqrt { m ^ { 2 } + 3 } } = \sqrt { \dfrac { 16 m ^ { 2 } + 16 m + 4 } { m ^ { 2 } + 3 } }\);
令\(f ( m ) = \dfrac { 16 m ^ { 2 } + 16 m + 4 } { m ^ { 2 } + 3 } = 16 + 4 \cdot \dfrac { 4 m - 11 } { m ^ { 2 } + 3 }\),
设\(t = 4 m - 11\),则\(m = \dfrac { t + 11 } { 4 }\),
所以\(\dfrac { 4 m - 11 } { m ^ { 2 } + 3 } = \dfrac { t } { \dfrac { t } { 16 } + 3 } = \dfrac { 16 t } { t ^ { 2 } + 22 t + 169 } = \dfrac { 16 } { t + \dfrac { 169 } { t } + 22 } \leq \dfrac { 16 } { 26 + 22 } = \dfrac { 1 } { 3 }\)
当\(t=13\),即\(m=6>1\)时取到等号,
所以\(f ( m ) = 16 + 4 \cdot \dfrac { 4 m - 11 } { m ^ { 2 } + 3 } \leq \dfrac { 52 } { 3 }\),
所以当\(m=6\)时,\(\dfrac { 2 } { e _ { 1 } } + \dfrac { 1 } { e_ 2 }\)取最大值\(\sqrt { \dfrac { 52 } { 3 } }\),此时\(\dfrac { A D } { D C } = \dfrac { 1 } { 6 }\),
【点拨】
①本题中没给出任一线段长度,设\(AG=1\),可减少计算量;
②本题求最值采取函数法,这是\(\dfrac { a _ { 1 } x _ { 2 } ^ { 2 } + b _ { 1 } x + c _ { 1 } } { a _ { 2 } x ^ { 2 } + b _ { 2 } x + c _ { 2 } }\)型的函数最值问题,此类题目常考.
巩固练习
1 (★★) 已知\(F_1 、F_2\)是双曲线\(\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左右焦点,以\(F_2\)为圆心,\(a\)为半径的圆与双曲线的一条渐近线交于\(A,B\)两点,若\(|AB|>\dfrac {|F_1 F_2 |}{2}\),则双曲线的离心率的取值范围是\(\underline{\quad \quad}\) .
2(★★) 设双曲线\(\dfrac{x^2}{16} -\dfrac{y^2}{12}=1\)的左、右焦点分别为\(F_1,F_2\),过\(F_1\)的直线\(l\)交双曲线左支于\(A,B\)两点,则\(|AF_2 |+|BF_2 |\)的最小值为\(\underline{\quad \quad}\).
3(★★) 已知\(F_1,F_2\)分别是双曲线\(C:\dfrac{x^2}{4} -\dfrac{y^2}{3}=1\)的左,右焦点,动点\(A\)在双曲线的左支上,点\(B\)为圆\(E:x^2+(y+3)^2=1\)上一动点,则\(|AB|+|AF_2 |\)的最小值为\(\underline{\quad \quad}\).
4(★★★)设双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左、右焦点分别为\(F_1,F_2\),\(|F_1 F_2 |=2c\),过\(F_2\)作\(x\)轴的垂线,与双曲线在一第象限的交点为\(A\),点\(Q\)坐标为\((c,\dfrac {3a}{2})\)且满足\(|F_2 Q|>|F_2 A|\),若在双曲线\(C\)的右支上存在点\(P\)使得\(|PF_1 |+|PQ|<\dfrac{7}{6}|F_1 F_2|\)成立,则双曲线\(C\)的离心率的取值范围是\(\underline{\quad \quad}\).
5(★★★) 双曲线\(C:\dfrac{x^2}{4}-y^2=1\)的左,右顶点分别是\(A_1,A_2\),\(P\)是\(C\)上任意一点,直线\(PA_1,PA_2\)分别与直线\(l:x=1\)交于\(M,N\),则\(|MN|\)的最小值是\(\underline{\quad \quad}\).
6(★★★) 已知双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左右焦点为\(F_1 (-2,0),F_2 (2,0)\),点\(P\)是双曲线上任意一点,若\(\overrightarrow{PF_1} \cdot \overrightarrow{PF_2}\)的最小值是\(-2\),则双曲线\(C\)的离心率为\(\underline{\quad \quad}\).
7(★★★) 已知双曲线\(C:\dfrac{x^2}{4}-y^2=1\),\(F_1,F_2\)分别为双曲线的左右焦点,\(P(x_0,y_0)\)为双曲线\(C\)上一点,且位于第一象限,若\(△PF_1 F_2\)为锐角三角形,则\(y_0\)的取值范围为\(\underline{\quad \quad}\).
8(★★★) 设双曲线\(C:\dfrac{x^2}{a^2} -\dfrac{y^2}{b^2}=1(a>0,b>0)\)的右焦点为\(F\),双曲线\(C\)的一条渐近线为\(l\),以\(F\)为圆心的圆与\(l\)交于点\(M,N\)两点,\(MF⊥NF\),\(O\)为坐标原点,\(\overrightarrow{OM}=\lambda\overrightarrow{ON}(3\leq\lambda\leq7)\),则双曲线\(C\)的离心率的取值范围是 \(\underline{\quad \quad}\).
参考答案
- \((1,\dfrac{2\sqrt10}{5})\)
- \(22\)
- \(7\)
- \((\dfrac{3}{2},\dfrac{\sqrt{10}}{2})\)
- \(\sqrt3\)
- \(\sqrt2\)
- \((\dfrac{\sqrt5}{5},\dfrac{1}{2})\)
- \([\dfrac{\sqrt5}{2},\dfrac{5}{4}]\)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号