6.1-6.2.3 平面向量的概念与运算
\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】高一数学下学期同步知识点剖析精品讲义!
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学,so \quad easy!}} }}}\)
必修第二册同步拔高,难度3颗星
模块导图
知识剖析
平面向量的概念
1 向量的概念
既有大小又有方向的量,常用\(\overrightarrow{A B}\),\(\vec{a}\)等表示;向量\(\overrightarrow{A B}\) 的长度是向量的模,记作\(|\overrightarrow{A B}|\).
\({\color{Red}{PS}}\) 平面向量在平面内是可以任意移动的.
2 常见向量的概念

\({\color{Red}{PS}}\)
\((1)\) 相等向量一定是共线向量,但共线向量不一定相等;
\((2)\) 平行向量无传递性!(因为有\(\overrightarrow{0}\));
\((3)\) 因为平面向量在平面内是可以任意移动的,与线段不一样,所以向量没有固定的起点和终点,两个向量平行与与两条直线平行是不同的两个概念.
图一线段\(AB\)和\(CD\), 在①中是\(AB//CD\),在②中是\(AB、CD\)共线;
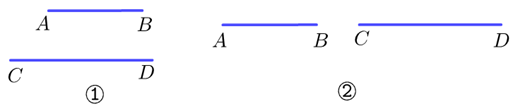
(图一)
图二向量\(\overrightarrow{A B}\)和\(\overrightarrow{CD}\), 对于向量来说共线与平行是同一概念,故①和②的情况是一样.
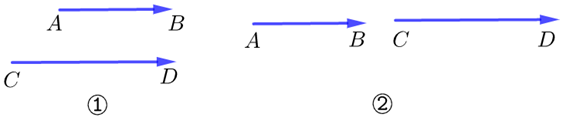
(图二)
平面向量的运算
1 向量的加法
① 向量加法的三角形法则
已知向量非零向量\(\vec{a}\),\(\vec{b}\)在平面内取任意一点\(A\), 作\(\overrightarrow{A B}=\vec{a}\),\(\overrightarrow{B C}=\vec{b}\),则向量\(\overrightarrow{AC}\)叫做\(\vec{a}\)与\(\vec{b}\)的和,记作\(\vec{a}+\vec{b}\),即\(\vec{a}+\vec{b}=\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}\).(相当于”首尾相接”)
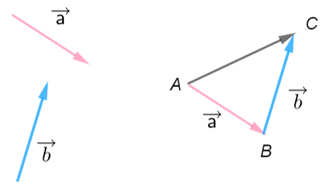
② 向量加法的平行四边形法则
若\(\overrightarrow{A B}=\vec{a}\), \(\overrightarrow{A D}=\vec{b}\),则向量\(\overrightarrow{AC}\)叫做 \(\vec{a}\)与\(\vec{b}\)的和,即\(\vec{a}+\vec{b}=\overrightarrow{A B}+\overrightarrow{A D}=\overrightarrow{A C}\);
作图
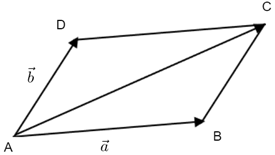
(\(ABCD\)是平行四边形)
2向量的减法
① 向量减法的几何意义
已知向量\(\vec{a}\),\(\vec{b}\), 在平面内任取一点\(O\),作\(\overrightarrow{O A}=\vec{a}\),\(\overrightarrow{O B}=\vec{b}\), 则\(\overrightarrow{B A}=\vec{a}-\vec{b}\),
即\(\vec{a}-\vec{b}\)可以表示向量\(\vec{b}\)的终点指向向量$\vec{a} $的终点的向量.
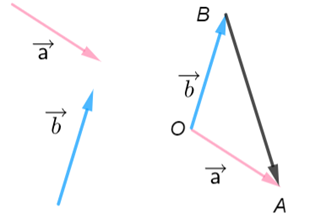
② 一般地 , 我们有
\({\LARGE {|\vec{a}+\vec{b}| \leq|\vec{a}|+|\vec{b}|}} \\\)
当且仅当\(\vec{a}\) ,\(\vec{b}\)方向相同时等号成立.
③ 向量的加减法满足交换律和结合律
④ 若\(\overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B}\)
(1) 如图一,若\(A ,B ,C\)三点共线,则\(x+y=1\);
(2) 如图二,若点\(O\)和点\(C\)在\(AB\)同侧,则\(x+y<1\);
(3) 如图三,若点\(O\)和点\(C\)在\(AB\)异侧,则\(x+y>1\);
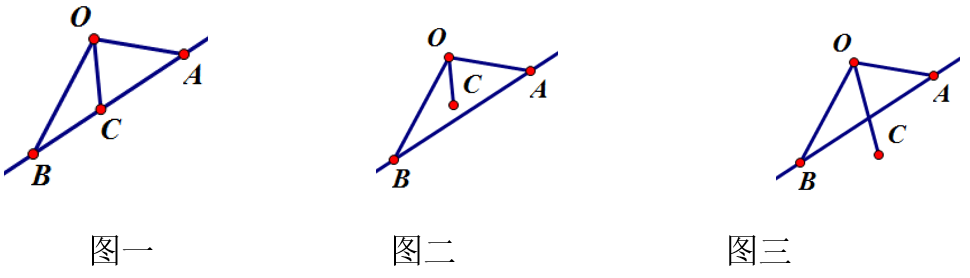
特殊的,在三角形\(∆ABC\)中,点\(D\)是\(BC\)的中点,则\(\overrightarrow{A D}=\dfrac{1}{2} \overrightarrow{A B}+\dfrac{1}{2} \overrightarrow{A C}\).
3 向量数乘运算
一般地,我们规定实数\(λ\)与向量 \(\vec{a}\)的积是一个向量,这种运算叫做向量的数乘,记作\(\lambda \vec{a}\);
它的长度与方向规定如下:
(1) \(|\lambda \vec{a}|=|\lambda||\vec{a}|\);
(2) 当\(λ>0\)时 ,\(\lambda \vec{a}\)的方向与\(\vec{a}\)的方向相同;
当\(λ<0\)时,\(\lambda \vec{a}\)的方向与\(\vec{a}\)方向相反;
4 两个向量共线
共线定理 非零向量\(\vec{a}\)与向量\(\vec{b}\)共线\(⇔\)有且只有一个实数\(λ\),使得\(\vec{b}=\lambda \vec{a}\).
当\(λ>0\)时 ,\(\lambda \vec{a}\)的方向与\(\vec{a}\)的方向相同;
当\(λ<0\) 时,\(\lambda \vec{a}\)的方向与\(\vec{a}\)方向相反;
当\(λ=0\) 时,\(\lambda \vec{a}=\overrightarrow{0}\).
数量积的概念
1 概念
如果两个非零向量\(\vec{a}\) ,\(\vec{b}\),它们的夹角为\(θ\),我们把数量\(|\vec{a}||\vec{b}| \cos \theta\)叫做\(\vec{a}\)与\(\vec{b}\)的数量积(或内积),记作:\(\vec{a} \cdot \vec{b}\),即\(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta\).
规定:零向量与任一向量的数量积是\(0\).
PS 数量积是一个实数,不再是一个向量.
2 投影
向量\(\vec{b}\)在向量\(\vec{a}\)上的投影:\(|\vec{b}| \cos \theta\),它是一个实数,但不一定大于\(0\).
3 运算法则
对于向量\(\vec{a}\) ,\(\vec{b}\) ,\(\vec{c}\)和实数\(λ\),有
(1)\(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)
(2)\((\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b})=\vec{a} \cdot(\lambda \vec{b})\)
(3)\((\vec{a}+\vec{b}) \cdot \vec{c}=\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}\)
但是\((\vec{a} \cdot \vec{b}) \vec{c}=\vec{a}(\vec{b} \cdot \vec{c})\)不一定成立.
(当向量\(\vec{a}\),\(\vec{c}\)不共线时,向量\(\vec{a}(\vec{b} \cdot \vec{c})\)与向量\((\vec{a} \cdot \vec{b}) \vec{c}\)肯定不共线,那怎么可能相等呢)
即向量的数量积满足交换律,分配率,但不满足结合律.
经典例题
【题型一】向量的相关概念
【典题1】 给出下列命题
① 向量\(\overrightarrow{AB}\)与\(\overrightarrow{CD}\)是共线向量,则\(A ,B ,C ,D\)四点必在一直线上;
② 若\(\vec{a}\) ,\(\vec{b}\)满足\(|\vec{a}|>|\vec{b}|\)且\(\vec{a}\)与\(\vec{b}\)同向,则\(\vec{a}> \vec{b}\);
③ 若\(\vec{a}=\vec{b}\), \(\vec{b}=\vec{c}\),则\(\vec{a}=\vec{c}\);
④ 若两个向量相等,则它们的起点和终点分别重合;
⑤ 若\(|\vec{a}|=|\vec{b}|\), 则\(\vec{a}=\vec{b}\);
⑥ 若\(\vec{a} || \vec{b}\),\(\vec{b}|| \vec{c}\),则\(\vec{a}|| \vec{c}\).
其中正确命题数是哪些?
【解析】 对于①,对于向量来说,共线向量即是平行向量,所以向量\(\overrightarrow{AB}\)与\(\overrightarrow{CD}\)是共线向量,\(A、B、C、D\)四点不一定在一直线上,①错误;
对于②,向量是有方向的量,不能比较大小,其模才能比较大小,故②错误;
对于③,若\(\vec{a}=\vec{b}\), \(\vec{b}=\vec{c}\), 则\(\vec{a}=\vec{c}\)成立,故③对;
对于④,向量是可以平移的矢量,当两个向量相等时,它们的起点和终点不一定相同,故④错误;
对于⑤,\(|\vec{a}|=|\vec{b}|\)只说明两个向量的模相等,要\(\vec{a}=\vec{b}\)还需要向量方向相同;
对于⑥,当\(\vec{b}\)为零向量时不成立,零向量与任何向量都平行.
【点拨】
① 向量是可以平移的矢量,没有固定的起点,共线向量即是平行向量 , 与线段、直线不一样;
② 零向量与任何向量都平行,在判断向量关系时要注意零向量的特殊情况.
【题型二】共线定理
【典题1】 点\(C\)在直线\(AB\)上,且\(|\overrightarrow{A C}|=\dfrac{2}{3}|\overrightarrow{C B}|\),若\(\overrightarrow{A B}=\lambda \overrightarrow{B C}\),则\(λ=\)\(\underline{\quad \quad}\).
【解析】\({\color{Red}{(点C在直线AB上,注意分类讨论)}}\)
\((1)\)当点\(C\)在线段\(AB\)上,如图所示;
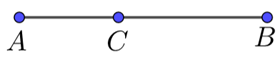
\(\because|A C|=\dfrac{2}{3}|B C|\), \(\therefore|A B|=\dfrac{5}{3}|B C|\) ;
若\(\overrightarrow{A B}=\lambda \overrightarrow{B C}\),则\(\lambda=-\dfrac{5}{3}\);
\((2)\)当点\(C\)在线段\(BA\)延长线上,如图所示;

\(\because|A C|=\dfrac{2}{3}|B C|\), \(\therefore|A B|=3|B C|\);
若\(\overrightarrow{A B}=\lambda \overrightarrow{B C}\),则\(λ=-3\);
【点拨】体会下线段比与向量比之间的相互转化,若\(\overrightarrow{A B}=\lambda \overrightarrow{B C}\),则\(\lambda=\dfrac{|A B|}{|B C|}\)或\(\lambda=-\dfrac{|A B|}{|B C|}\).
【题型三】向量的加减法
【典题1】 若\(|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|\),则\(\vec{a}\)与\(\vec{b}\)的夹角为________.
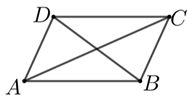
【解析】 构造平行四边形\(ABCD\),\(|\vec{a}+\vec{b}|\),\(|\vec{a}-\vec{b}|\)分别对角线\(BD\) ,\(AC\),因为\(|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|\),所以平行四边形\(ABCD\)的对角线相等,即\(ABCD\)是矩形,故\(\vec{a}\)与\(\vec{b}\)的的夹角为\(90°\).
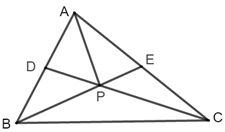
【典题2】 在\(△ABC\)中,\(D\),\(E\)分别为边\(AB\),\(AC\)的中点,\(BE\)与\(CD\)交于点\(P\),设\(\overrightarrow{A B}=\vec{a}\),\(\overrightarrow{A C}=\vec{b}\),则\(\overrightarrow{A P}=\) ( )
A.\(\dfrac{1}{3} \vec{a}+\dfrac{1}{3} \vec{b}\)
B.\(\dfrac{2}{3} \vec{a}+\dfrac{2}{3} \vec{b}\)
C.\(\dfrac{3}{4} \vec{a}+\dfrac{3}{4} \vec{b}\)
D.\(\dfrac{1}{6} \vec{a}+\dfrac{1}{6} \vec{b}\)
【解析】 \({\color{Red}{方法1 首尾相接法}}\)
\(\begin{aligned}
&\overrightarrow{A P}=\overrightarrow{A B}+\overrightarrow{B P} \\
&=\overrightarrow{A B}+\lambda \overrightarrow{B E}=\overrightarrow{A B}+\lambda(\overrightarrow{B A}+\overrightarrow{A E}) \\
&=\overrightarrow{A B}+\lambda\left(\overrightarrow{B A}+\dfrac{1}{2} \overrightarrow{A C}\right) \\
&=(1-\lambda) \overrightarrow{A B}+\dfrac{\lambda}{2} \overrightarrow{A C}=(1-\lambda) \vec{a}+\dfrac{\lambda}{2} \vec{b}, \text { 其中 } \lambda=\dfrac{B P}{B E}
\end{aligned}\)
\({\color{Red}{(利用平几知识点求出λ)}}\)
如图过点\(E\)作\(EF//AB\),
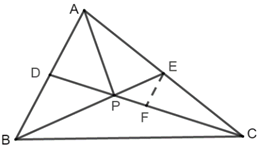
\(∵E、D\)是中点,\(\therefore E F=\dfrac{1}{2} A D=\dfrac{1}{2} B D\)
\(\therefore \dfrac{B P}{B E}=\dfrac{2}{3}\) 即\(\lambda=\dfrac{2}{3}\)
\(\therefore \overrightarrow{A P}=(1-\lambda) \vec{a}+\dfrac{\lambda}{2} \vec{b}=\dfrac{1}{3} \vec{a}+\dfrac{1}{3} \vec{b}\)
\({\color{Red}{方法2 构造平行四边形法}}\)
过点\(P\)分别作\(PH//AB\) ,\(PG//AC\) , 则四边形\(AGPH\)是平行四边形,
则\(\overrightarrow{A P}=\overrightarrow{A G}+\overrightarrow{A H}=x \overrightarrow{A B}+y \overrightarrow{A C}=x \vec{a}+y \vec{b}\),
其中\(x=\dfrac{A G}{A B}\),\(y=\dfrac{A H}{A C}\)
\({\color{Red}{(问题化为线段比值问题)}}\)
由方法1可得\(\dfrac{B P}{B E}=\dfrac{2}{3}\)
\(\because x=\dfrac{A G}{A B}=\dfrac{P E}{B E}=\dfrac{B E-B P}{B E}\)\(=1-\dfrac{B P}{B E}=1-\dfrac{2}{3}=\dfrac{1}{3}\),
同理可得\(y=\dfrac{1}{3}\)
\(\therefore \overrightarrow{A P}=\dfrac{1}{3} \vec{a}+\dfrac{1}{3} \vec{b}\).
\({\color{Red}{方法3}}\) \(△ABC\)中,\(D ,E\)分别为边\(AB ,AC\)的中点,
\(\therefore \overrightarrow{A D}=\dfrac{1}{2} \overrightarrow{A B}, \overrightarrow{A E}=\dfrac{1}{2} \overrightarrow{A C}\).
\(∵B ,P ,E\)三点共线,
设\(\overrightarrow{A P}=m \overrightarrow{A B}+(1-m) \overrightarrow{A E}\)\(=m \overrightarrow{A B}+\dfrac{1}{2}(1-m) \overrightarrow{A C}\),
\(∵C ,P ,D\)三点共线,
设\(\overrightarrow{A P}=n \overrightarrow{A D}+(1-n) \overrightarrow{A C}\)\(=\dfrac{1}{2} n \overrightarrow{A B}+(1-n) \overrightarrow{A C}\),
\(\therefore\left\{\begin{array}{l}
m=\dfrac{1}{2} n \\
\dfrac{1}{2}(1-m)=1-n
\end{array}\right.\),解得\(\left\{\begin{array}{l}
m=\dfrac{1}{3} \\
n=\dfrac{2}{3}
\end{array}\right.\),
\(\therefore \overrightarrow{A P}=\dfrac{1}{3} \overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{A C}=\dfrac{1}{3} \vec{a}+\dfrac{1}{3} \vec{b}\).
故选:\(A\).
【点拨】
① 本题是用向量\(\overrightarrow{A B}=\vec{a}, \overrightarrow{A C}=\vec{b}\)表示\(\overrightarrow{A P}\);
② 方法1是利用三角形法则,“首尾相接法” , 思路是:先找到一个含\(AP\)的封闭图形,比如\(∆ABP\) , 则有\(\overrightarrow{A P}=\overrightarrow{A B}+\overrightarrow{B P}\),接着\(\overrightarrow{B P}\)尽量向向量\(\overrightarrow{A B}\),\(\overrightarrow{A C}\)凑拢,得到\(\overrightarrow{A P}=(1-\lambda) \vec{a}+\dfrac{\lambda}{2} \vec{b}\)后就只需要求出\(\lambda=\dfrac{B P}{B E}\)就行;
③ 方法2是构造平行四边形法:构造邻边在\(AB ,AC\)所在的直线上,\(AP\)为对角线的平行四边形,再利用平行线成比例的性质与其他的几何知识求解便可;
④ 方法3是使用向量性质:在\(∆ABC\)中,点\(D\)在边\(BD\)上,则存在\(x\),使得\(\overrightarrow{A D}=x \overrightarrow{A B}+y \overrightarrow{A C}\),其中\(x+y=1\).
【典题3】 点\(O\)在\(△ABC\)的内部,且满足\(\overrightarrow{O A}+2 \overrightarrow{O B}+4 \overrightarrow{O C}=\overrightarrow{0}\),则\(△ABC\)的面积与\(△AOC\)的面积之比是\(\underline{\quad \quad}\).
【解析】如图所示,作\(OD=4OC\),以\(OA,OD\)为邻边作平行四边形\(OAED\),连接\(OE\)交\(AC\)于点\(N\).
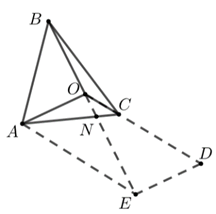
\(∵\)满足\(\overrightarrow{O A}+2 \overrightarrow{O B}+4 \overrightarrow{O C}=\overrightarrow{0}\),
\(\therefore \overrightarrow{O A}+4 \overrightarrow{O C}=-2 \overrightarrow{O B}\),
由\(\triangle O C N \sim \triangle E A M\)可得\(\dfrac{O N}{N E}=\dfrac{O C}{A E}=\dfrac{1}{4}\),
\({\color{Red}{(利用平行四边形性质,注意图象中的8字型,A字型)}}\)
\(\therefore|O N|=\dfrac{1}{5}|O E|=\dfrac{2}{5}|O B|\),\(\therefore|O N|=\dfrac{2}{7}|B N|\)
\(∴△ABC\)的面积与\(△AOC\)的面积之比是\(7:2\).
\({\color{Red}{(利用等高,三角形面积的比等于底的比,\dfrac{S_{\triangle A B C}}{S_{\triangle A O C}}=\dfrac{S_{\triangle A B N}+S_{\triangle C B N}}{S_{\triangle A O N}+S_{\triangle C O N}}=\dfrac{\dfrac{7}{2} S_{\triangle A O N}+\dfrac{7}{2} S_{\triangle C O N}}{S_{\triangle A O N}+S_{\triangle C O N}}=\dfrac{7}{2}})}\)
【点拨】
① 线段的比与向量之间的比可相互之间转化,比如题目中由\(\dfrac{O N}{N E}=\dfrac{1}{4} \Rightarrow \overrightarrow{O N}=\dfrac{1}{5} \overrightarrow{O E}\) , 要求\(\dfrac{B N}{O N}\)则只需要求向量\(\overrightarrow{B N}\)与\(\overrightarrow{O N}\)的倍数关系;
② 求解两个三角形的面积之比,可利用两个三角形等高,把问题转化为求解边长之比.
③ 类似题中已知条件\(\overrightarrow{O A}+2 \overrightarrow{O B}+4 \overrightarrow{O C}=\overrightarrow{0}\)是含三个向量的等式,可努力转化为两个向量的关系\(\overrightarrow{O A}+2 \overrightarrow{O B}+4 \overrightarrow{O C}=\overrightarrow{0} \Rightarrow \overrightarrow{O A}+4 \overrightarrow{O C}\)\(=-2 \overrightarrow{O B} \Rightarrow \overrightarrow{O E}=-2 \overrightarrow{O B}\),这里利用了构造平行四边形的手段\(\overrightarrow{O A}+4 \overrightarrow{O C}=\overrightarrow{O E}\),其实也可变形成\(\overrightarrow{O A}+2 \overrightarrow{O B}+4 \overrightarrow{O C}=\overrightarrow{0} \Rightarrow \overrightarrow{O A}+2 \overrightarrow{O B}=-4 \overrightarrow{O C}\),根据题目需求来便可.
巩固练习
1(★) 对下列命题:
(1)若向量\(\vec{a}\)与\(\vec{b}\)同向,且\(|\vec{a}|>|\vec{b}|\),则\(\vec{a}>\vec{b}\);
(2)若向量\(|\vec{a}|=|\vec{b}|\),则\(\vec{a}\)与\(\vec{b}\)的长度相等且方向相同或相反;
(3)对于任意向量\(|\vec{a}|=|\vec{b}|\),若\(\vec{a}\)与\(\vec{b}\)的方向相同,则\(\vec{a}=\vec{b}\);
(4)由于\(\overrightarrow{0}\)方向不确定,故\(\overrightarrow{0}\)不与任意向量平行;
(5)向量\(\vec{a}\)与\(\vec{b}\)平行,则向量\(\vec{a}\)与\(\vec{b}\)方向相同或相反.
其中正确的命题的个数为 .
2(★) 在\(△ABC\)中,\(\overrightarrow{A B}=\vec{a}\),\(\overrightarrow{A C}=\vec{b}\),若点\(D\)满足\(\overrightarrow{B D}=2 \overrightarrow{D C}\),则\(\overrightarrow{AD}\)______.(用\(\vec{a} ,\vec{b}\)表示)
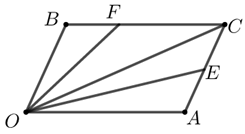
3(★★) 如图,在\(▱OACB\)中,\(E\)是\(AC\)的中点,\(F\)是\(BC\)上的一点,且\(BC=3BF\),若\(\overrightarrow{O C}=m \overrightarrow{O E}+n \overrightarrow{O F}\),其中\(m ,n∈R\),则\(m+n\)的值为______.
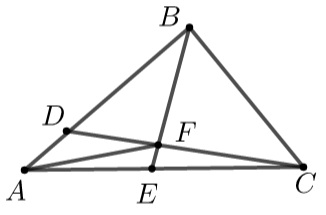
4(★★) 如图,在\(△ABC\)中,\(\overrightarrow{A D}=\dfrac{1}{4} \overrightarrow{A B}\),\(\overrightarrow{A E}=\dfrac{1}{2} \overrightarrow{A C}\),\(BE\)和\(CD\)相交于点\(F\),则向量\(\overrightarrow{A F}\)等于______.
5(★★★) 设\(G\)是\(△ABC\)的重心,\(a ,b ,c\)分别是角\(A ,B ,C\)所对的边,若\(a \overrightarrow{G A}+b \overrightarrow{G B}+c \overrightarrow{G C}=\overrightarrow{0}\),则\(△ABC\)的形状是\(\underline{\quad \quad}\) .
6(★★★)已知点\(O\)是\(△ABC\)内部一点,并且满足\(\overrightarrow{O A}+2 \overrightarrow{O B}+3 \overrightarrow{O C}=\overrightarrow{0}\),\(△BOC\)的面积为\(S_1\),\(△ABC\)的面积为\(S_2\),则\(\dfrac{S_{1}}{S_{2}}=\)\(\underline{\quad \quad}\).
7(★★★) 在\(△ABC\)中,\(E ,F\)分别为\(AB ,AC\)中点,\(P\)为线段\(EF\)上任意一点,实数\(x ,y\)满足\(\overrightarrow{P A}+x \overrightarrow{P B}+y \overrightarrow{P C}=\overrightarrow{0}\),设\(△ABC\),\(△PCA\),\(△PAB\)的面积分别为\(S\) ,\(S_1\),\(S_2\),记\(\dfrac{S_{1}}{S}=\lambda_{1}\),\(\dfrac{S_{2}}{S}=\lambda_{2}\),则\(λ_1 λ_2\)取得最大值时,\(2x+3y\)的值为\(\underline{\quad \quad}\).
8(★★★) 已知\(G\)是\(△ABC\)的重心,直线\(EF\)过点\(G\)且与边\(AB\)、\(AC\)分别交于点\(E、F\),\(\overrightarrow{A E}=\alpha \overrightarrow{A B}\),\(\overrightarrow{A F}=\beta \overrightarrow{A C}\),则\(\dfrac{1}{\alpha}+\dfrac{1}{\beta}\)的值为\(\underline{\quad \quad}\).
9(★★★) 已知平面向量\(\vec{a}, \vec{b}, \vec{c}\)满足\(|\vec{a}|=|\vec{b}|=|\vec{c}|=1\),\(\vec{a} \perp \vec{b}\),则\(|2 \vec{c}-\vec{a}|+\left|\dfrac{1}{2} \vec{c}-\vec{b}\right|\)的最小值为\(\underline{\quad \quad}\).
答案
- \(1\)
- \(\dfrac{2}{3} \vec{b}+\dfrac{1}{3} \vec{a}\)
- \(\dfrac{7}{5}\)
- \(\dfrac{1}{7} \overrightarrow{A B}+\dfrac{3}{7} \overrightarrow{A C}\)
- 等边三角形
- \(\dfrac{1}{6}\)
- \(\dfrac{5}{2}\)
- \(3\)
- \(\sqrt{5}\)
【题型四】数量积问题
情况1 求数量积
【典题1】 已知向量\(\vec{a}\),\(\vec{b}\)满足\(|\vec{a}+\vec{b}|=|\vec{b}|\),且\(|\vec{a}|=2\),则\(\vec{a} \cdot \vec{b}=\)\(\underline{\quad \quad}\).
【解析】因为\(|\vec{a}+\vec{b}|=|\vec{b}|\),即有\(|\vec{a}+\vec{b}|^{2}=|\vec{b}|^{2}\),
所以\(\vec{a}^{2}+2 \vec{a} \cdot \vec{b}+\vec{b}^{2}=\vec{b}^{2}\),
则\(2 \vec{a} \cdot \vec{b}=-\vec{a}^{2}=-4\),
所以\(\vec{a} \cdot \vec{b}=-2\).
【点拨】① 由数量积的定义可知\(|\vec{a}|^{2}=\vec{a}^{2}\)
② 题目中遇到类似\(|\vec{a}+\vec{b}|\)可尝试利用性质\(|\vec{a}|^{2}=\vec{a}^{2}\)达到去掉绝对值的目的.
【典题2】 在三角形\(ABC\)中,若\(|\overrightarrow{A B}+\overrightarrow{B C}|=|\overrightarrow{A B}-\overrightarrow{B C}|\),\(AC=6\),\(AB=3\),\(E\),\(F\)为\(BC\)边的三等分点,则\(\overrightarrow{A E} \cdot \overrightarrow{A F}=\)\(\underline{\quad \quad}\).
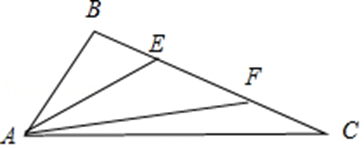
【解析】 若\(|\overrightarrow{A B}+\overrightarrow{B C}|=|\overrightarrow{A B}-\overrightarrow{B C}|\),
则\(\overrightarrow{A B}^{2}+\overrightarrow{B C}^{2}+2 \overrightarrow{A B} \cdot \overrightarrow{B C}=\overrightarrow{A B}^{2}+\overrightarrow{B C}^{2}-2 \overrightarrow{A B} \cdot \overrightarrow{B C}\),
即有\(\overrightarrow{A B} \cdot \overrightarrow{B C}=0\),
\(∵AC=6 ,AB=3\),
\(\therefore B C^{2}=6^{2}-3^{2}=27\)
\(∵E ,F\)为\(BC\)边的三等分点,
则\(\overrightarrow{A E} \cdot \overrightarrow{A F}=(\overrightarrow{A B}+\overrightarrow{B E})(\overrightarrow{A B}+\overrightarrow{B F})\)\(=\left(\overrightarrow{A B}+\dfrac{1}{3} \overrightarrow{BC}\right)\left(\overrightarrow{A B}+\dfrac{2}{3} \overrightarrow{B C}\right)\)
\({\color{Red}{(利用首尾相接法把向量向\overrightarrow{A B},\overrightarrow{B C}靠拢)}}\)
\(=\dfrac{2}{9} \overrightarrow{B C}^{2}+\overrightarrow{A B}^{2}+\overrightarrow{A B} \cdot \overrightarrow{B C}=\dfrac{2}{9} \times 27+3^{2}+0=15\).
【点拨】
① 已知条件\(|\overrightarrow{A B}+\overrightarrow{B C}|=|\overrightarrow{A B}-\overrightarrow{B C}|\)利用性质\(|\vec{a}|^{2}=\vec{a}^{2}\)可得到\(\overrightarrow{A B} \cdot \overrightarrow{B C}=0\),其实也可以通过平行四边形法则和三角形法则得到的;
② 求数量积\(\overrightarrow{A E} \cdot \overrightarrow{A F}\) , 第一个想法用数量积公式\(\overrightarrow{A E} \cdot \overrightarrow{A F}=|\overrightarrow{A E}| \cdot|\overrightarrow{A F}| \cos \angle E A F\), 但是发现题目已知条件中很难求解\(|\overrightarrow{A E}|\),\(|\overrightarrow{A F}|\),\(\cos \angle E A F\).又因为\(\overrightarrow{A B} \cdot \overrightarrow{B C}=0\),又知道\(AB、BC\)的长度,故想到把\(\overrightarrow{A E} \cdot \overrightarrow{A F}\)转化为用\(\overrightarrow{A B}, \overrightarrow{B C}\)表示.
③ 在求数量积的时候,直接用公式很难求解,都尽量向“信息量大”的向量靠拢.
情况2 求向量夹角
【典题1】 已知向量\(\vec{a}, \vec{b}\)满足\(|\vec{a}|=1\),\(|\vec{b}|=2\),\(|\vec{a}+2 \vec{b}|=\sqrt{21}\),那么向量\(\vec{a}\)与\(\vec{b}\)的夹角为\(\underline{\quad \quad}\).
【解析】\(∵|\vec{a}|=1\),\(|\vec{b}|=2\),\(|\vec{a}+2 \vec{b}|=\sqrt{21}\),
\(\therefore(\vec{a}+2 \vec{b})^{2}=\vec{a}^{2}+4 \vec{b}^{2}+4 \vec{a} \cdot \vec{b}\)\(=1+16+4 \vec{a} \cdot \vec{b}=21\),
\(\therefore \vec{a} \cdot \vec{b}=1\),
\(\therefore \cos <\vec{a}, \vec{b}>=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{1}{2}\),且\(0 \leq<\vec{a}, \vec{b}>\leq \pi\),
\(\therefore \vec{a}\)与\(\vec{b}\)的夹角为\(\dfrac{\pi}{3}\).
【典题2】 已知向量\(\vec{a}, \vec{b}\)满足\(|\vec{a}|=1\),\((\vec{a}-\vec{b}) \perp(3 \vec{a}-\vec{b})\),则\(\vec{a}\)与\(\vec{b}\)的夹角的最大值为\(\underline{\quad \quad}\).
【解析】 \(\because|\vec{a}|=1\),\((\vec{a}-\vec{b}) \perp(3 \vec{a}-\vec{b})\)
\(\therefore(\vec{a}-\vec{b}) \cdot(3 \vec{a}-\vec{b})=3 \vec{a}^{2}+\vec{b}^{2}-4 \vec{a} \cdot \vec{b}\)\(=3+\vec{b}^{2}-4 \vec{a} \cdot \vec{b}=0\),
\(\therefore \vec{a} \cdot \vec{b}=\dfrac{|\vec{b}|^{2}+3}{4}\),
\(\therefore \cos <\vec{a}, \vec{b}>=\dfrac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}=\dfrac{|\vec{b}|^{2}+3}{4|\vec{b}|}\)\(=\dfrac{|\vec{b}|+\dfrac{3}{|\vec{b}|}}{4} \geq \dfrac{\sqrt{3}}{2}\),且\(0^{\circ} \leq<\vec{a}, \vec{b}>\leq 180^{\circ}\),
\(\therefore \cos <\vec{a}, \vec{b}>=\dfrac{\sqrt{3}}{2}\)时,\(\vec{a}, \vec{b}\)的夹角最大为\(30°\).
情况3 求数量积最值
【典题1】 如图,已知等腰梯形\(ABCD\)中,\(AB=2DC=4\),\(A D=B C=\sqrt{3}\),\(E\)是\(DC\)的中点,\(F\)是线段\(BC\)上的动点,则\(\overrightarrow{E F} \cdot \overrightarrow{B F}\)的最小值是\(\underline{\quad \quad}\).
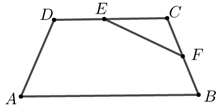
【解析】 由等腰梯形的知识可知\(\cos B=\dfrac{\sqrt{3}}{3}\),
设\(BF=x\),则\(C F=\sqrt{3}-x\),
\(\therefore \overrightarrow{E F} \cdot \overrightarrow{B F}=(\overrightarrow{E C}+\overrightarrow{C F}) \overrightarrow{B F}\)\(=\overrightarrow{E C} \cdot \overrightarrow{B F}+\overrightarrow{C F} \cdot \overrightarrow{B F}\)
\(=1 \cdot x\left(-\dfrac{\sqrt{3}}{3}\right)+(\sqrt{3}-x) \cdot x \cdot(-1)\)\(=x^{2}-\dfrac{4}{3} \sqrt{3} x\),
\(\because 0 \leq x \leq \sqrt{3}\),
\(∴\)当\(x=\dfrac{2}{3} \sqrt{3}\)时,\(\overrightarrow{E F} \cdot \overrightarrow{B F}\)取得最小值,最小值为\(\left(\dfrac{2}{3} \sqrt{3}\right)^{2}-\dfrac{2}{3} \sqrt{3} \times \dfrac{4}{3} \sqrt{3}=-\dfrac{4}{3}\).
【典题2】 如图,已知矩形\(ABCD\)的边长\(AB=2\) ,\(AD=1\).点\(P,Q\)分别在边\(BC\),\(CD\)上,且\(∠PAQ=45°\),则\(\overrightarrow{A P} \cdot \overrightarrow{A Q}\)的最小值为\(\underline{\quad \quad}\).
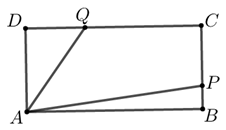
【解析】 设\(∠PAB=θ\),则\(∠DAQ=45°-θ\),
\(\overrightarrow{A P} \cdot \overrightarrow{A Q}=|\overrightarrow{A P}||\overrightarrow{A Q}| \cos 45^{\circ}\)\(=\dfrac{2}{\cos \theta} \cdot \dfrac{1}{\cos \left(45^{\circ}-\theta\right)} \cdot \dfrac{\sqrt{2}}{2}=\dfrac{2}{\cos \theta \cdot\left(\dfrac{\sqrt{2}}{2} \cos \theta+\dfrac{\sqrt{2}}{2} \sin \theta\right)}\),
\(=\dfrac{2}{\cos ^{2} \theta+\cos \theta \sin \theta}\)\(=\dfrac{2}{\dfrac{1+\cos 2 \theta}{2}+\dfrac{\sin 2 \theta}{2}}\)\(=\dfrac{2}{\dfrac{\sqrt{2}}{2} \sin \left(2 \theta+45^{\circ}\right)+\dfrac{1}{2}}\geq \dfrac{2}{\dfrac{\sqrt{2}}{2}+\dfrac{1}{2}}=4 \sqrt{2}-4\),
当且仅当\(2θ+45°=90°\),
\(∴θ=22.5°\)时取\(“=”\),当\(θ=22.5°\)时,点\(P\)恰在边\(BC\)上,\(Q\)恰边\(CD\)上,满足条件,
综上所述,\(\overrightarrow{A P} \cdot \overrightarrow{A Q}\)的最小值为\(4 \sqrt{2}-4\).
【典题3】 已知向量\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)满足\(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\),\(|\vec{c}|=2 \sqrt{3}\),\(\vec{c}\)与\(\vec{a}-\vec{b}\)所成的角为\(120°\),则当\(t∈R\)时,\(|t \vec{a}+(1-t) \vec{b}|\)的最小值是\(\underline{\quad \quad}\).
【解析】

\(∵\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\),\(\therefore \vec{c}=-(\vec{a}+\vec{b})\),
又\(\vec{c}\)与\(\vec{a}-\vec{b}\)所成的角为\(120°\),\(∴∠OEA=120°\),
\({\color{Red}{(此时由平行四边形法则和三角形法则构造出一个平行四边形OADB)}}\)
\(∴∠OEB=60°\), \(|\vec{c}|=2 \sqrt{3}\),
\(\therefore O D=2 \sqrt{3}\),\(O E=\sqrt{3}\)
\(|t \vec{a}+(1-t) \vec{b}|=|\vec{b}+t(\vec{a}-\vec{b})|=|\overrightarrow{O B}+t \overrightarrow{B A}|\),
\(\because \overrightarrow{B P}\)与\(\overrightarrow{B A}\)共线,\(\overrightarrow{B A} \neq \overrightarrow{0}\),设\(\overrightarrow{B P}=t \overrightarrow{B A}\),
则\(|t \vec{a}+(1-t) \vec{b}|=|\overrightarrow{O P}|\)(\(P\)是直线\(BA\)上的动点),
\({\color{Red}{(其实由性质“若\overrightarrow{O C}=x \overrightarrow{O A}+y \overrightarrow{O B},x+y=1, 则点C在直线AB上”很容易知道:直线BA上的存在一动点P, 使得\overrightarrow{O P}=t \vec{a}+(1-t) \vec{b})}}\)
所以当\(OP\)垂直于\(AB\)时,\(|t \vec{a}+(1-t) \vec{b}|=|\overrightarrow{O P}|\)最小,为\(O E \times \sin 60^{\circ}=\sqrt{3} \times \dfrac{\sqrt{3}}{2}=\dfrac{3}{2}\).
【点拨】① 题中遇到类似\(\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}\)的等式,很容易想到移项,再利用平行四边形法则进行构造图形求解;**② 本题中求\(|t \vec{a}+(1-t) \vec{b}|\)的最小值,那我们根据平行四边形法则找到向量\(t \vec{a}+(1-t) \vec{b}\), 确定出\(|t \vec{a}+(1-t) \vec{b}|\)的几何意义从而求解成功.
巩固练习
1(★) 已知向量\(\vec{a}\),\(\vec{b}\)满足\(|\vec{a}+\vec{b}|=|\vec{b}|\),且\(|\vec{a}|=2\),则\(\vec{a} \cdot \vec{b}=\)\(\underline{\quad \quad}\).
2(★★) 已知非零向量\(\vec{a}\),\(\vec{b}\)满足\(|\vec{a}|=\dfrac{3}{4}|\vec{b}|\),\(\cos <\vec{a}, \quad \vec{b}>=\dfrac{1}{3}\),若\((m \vec{a}+4 \vec{b}) \perp \vec{b}\),则实数\(m\)的值为\(\underline{\quad \quad}\) .
3(★★) 已知向量\(\vec{a}\),\(\vec{b}\)满足\(|\vec{a}|=1\),\((\vec{a}-\vec{b}) \perp(3 \vec{a}-\vec{b})\),则\(\vec{a}\)与\(\vec{b}\)的夹角的最大值为\(\underline{\quad \quad}\).
4(★★) 如图,在梯形\(ABCD\)中,\(AB∥CD\) ,\(AB=4\) ,\(AD=3\),\(CD=2\),\(\overrightarrow{A M}=2 \overrightarrow{M D}\),\(\overrightarrow{A C} \cdot \overrightarrow{B M}=-3\),则\(\overrightarrow{A B} \cdot \overrightarrow{A D}=\) \(\underline{\quad \quad}\).
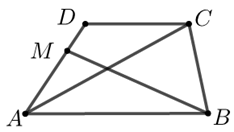
5(★★)已知\(△ABC\)中,点\(M\)在线段\(AB\)上,\(∠ACB=2∠BCM=60°\),且\(\overrightarrow{C M}-\lambda \overrightarrow{C B}=\dfrac{2}{3} \overrightarrow{C A}\).若\(|\overrightarrow{C M}|=6\),则\(\overrightarrow{C M} \cdot \overrightarrow{A B}=\)\(\underline{\quad \quad}\).
6(★★★) 设\(H\)是\(△ABC\)的垂心,且\(3 \overrightarrow{H A}+4 \overrightarrow{H B}+5 \overrightarrow{H C}=\overrightarrow{0}\),则\(cos∠BHC\)的值为\(\underline{\quad \quad}\).
7(★★★)已知P为\(△ABC\)所在平面内的一点,\(\overrightarrow{B P}=2 \overrightarrow{P C}\),\(|\overrightarrow{A P}|=4\),若点\(Q\)在线段\(AP\)上运动,则\(\overrightarrow{Q A} \cdot(\overrightarrow{Q B}+2 \overrightarrow{Q C})\)的最小值为\(\underline{\quad \quad}\).
8(★★★) 已知非零向量\(\vec{a}\),\(\vec{b}\) ,\(\vec{c}\)足:\((\vec{a}-2 \vec{c})(\vec{b}-2 \vec{c})=0\)且不等式
\(|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}| \geq \lambda|\vec{c}|\)恒立,则实数\(λ\)的最大值为\(\underline{\quad \quad}\).
9(★★★) 已知平面向量\(\vec{a}\),\(\vec{b}\) ,\(\vec{c}\),对任意实数\(x,y\)都有\(|\vec{a}-x \vec{b}| \geq|\vec{a}-\vec{b}|\),\(|\vec{a}-y \vec{c}| \geq|\vec{a}-\vec{c}|\)成立.若\(|\vec{a}|=2\),则\(\vec{b}(\vec{c}-\vec{a})\)的最大值是\(\underline{\quad \quad}\).
10(★★★) 设\(θ\)为两个非零向量\(\vec{a}\),\(\vec{b}\)的夹角,已知对任意实数\(t\),\(|\vec{b}-t \vec{a}|\)的最小值为\(1\),则( )
A.若\(θ\)确定,则\(|\vec{a}|\)唯一确定
B.若\(θ\)确定,则\(|\vec{b}|\)唯一确定
C.若\(|\vec{a}|\)确定,则\(θ\)唯一确定
D.若\(|\vec{b}|\)确定,则\(θ\)唯一确定
答案
- \(-2\)
- \(-16\)
- \(30°\)
- \(\dfrac{3}{2}\)
- \(27\)
- \(-\dfrac{\sqrt{70}}{14}\)
- \(-12\)
- \(4\)
- \(\dfrac{1}{2}\)
- \(B\)

