6.5 解三角形

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高一数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

必修第二册同步拔高，难度4颗星

模块导图

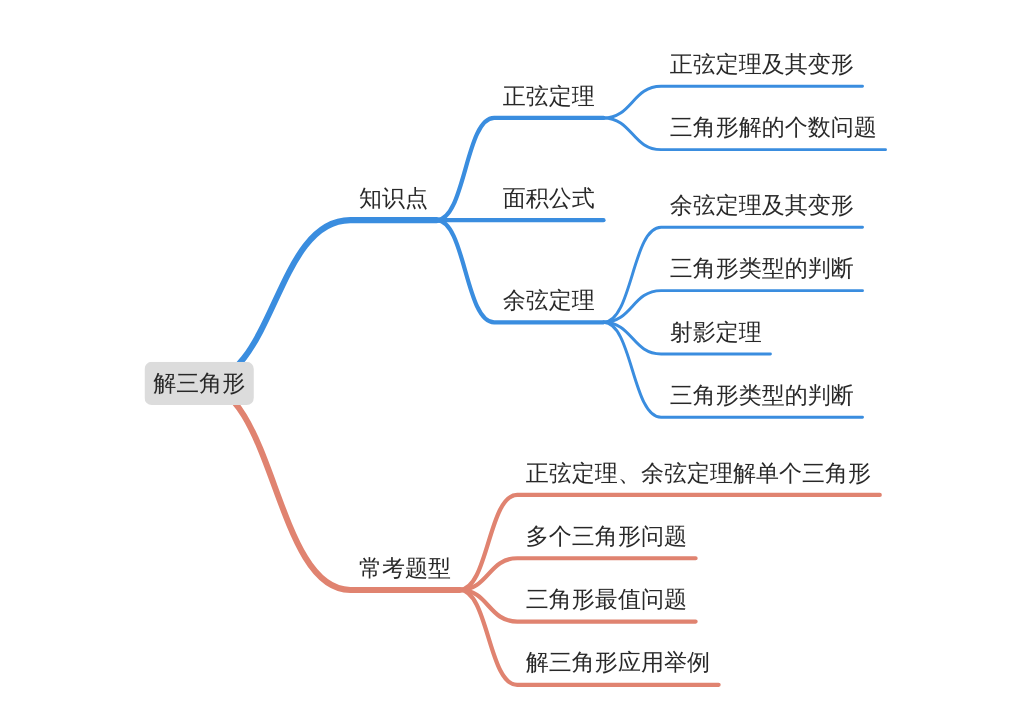
知识剖析

正弦定理

\(1\) 正弦定理

\[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2 R \]

(其中\(R\)是三角形外接圆半径)
 

\(2\) 变形
\((1)\) \(\dfrac{a+b+c}{\sin A+\sin B+\sin C}=\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\((2)\) 化边为角
\(a=2R \sin⁡A\) ,\(b=2 R \sin B\)，\(c=2 R \sin C\)
\(a: b: c=\sin A: \sin B: \sin C\) ,
\(\dfrac{a}{b}=\dfrac{\sin A}{\sin B}\)，\(\dfrac{b}{c}=\dfrac{\sin B}{\sin C}\)，\(\dfrac{a}{c}=\dfrac{\sin A}{\sin C}\)
\((3)\) 化角为边
\(\sin A=\dfrac{a}{2 R}, \sin B=\dfrac{b}{2 R}, \sin C=\dfrac{c}{2 R}\)
\(\dfrac{\sin A}{\sin B}=\dfrac{a}{b}, \dfrac{\sin B}{\sin C}=\dfrac{b}{c}, \dfrac{\sin A}{\sin C}=\dfrac{a}{c}\)
 

\(3\)正弦定理的“齐次角边互换”

等式\((*)\)中含有三个式子\((a \cdot \sin B，c \cdot \sin C，b \cdot \sin C)\)，每个式子中都有一个\(\sin\)值，并且它们的次数都是\(1\)，则可以把\(\sin B, \sin C\)直接转化为对应的边\(b、c\)！
同理\({\color{Red}{a}} \cdot \sin B+{\color{Red}{c }} \cdot \sin C={\color{Red}{ b}} \cdot \sin C\Rightarrow {\color{Red}{\sin A}} \cdot \sin B+{\color{Red}{\sin C }} \cdot \sin C={\color{Red}{\sin B }} \cdot \sin C\).
思考以下转化是否正确
\(\text { (1) } a \cdot \sin B+c \cdot \sin C=b \Rightarrow a \cdot b+c \cdot c=b\)(错)，
\(\text { (2) } \sin A \cdot \sin B+\sin B \cdot \sin C=\sin ^{2} A \Rightarrow a \cdot b+b \cdot c=a^{2}\) (对)
 

\(4\) 利用正弦定理可以解决下列两类三角形的问题
\((1)\)已知两个角及任意—边，求其他两边和另一角；
\({\color{Red}{Eg}}\) 在\(△ABC\)，内角\(A ,B ,C\)所对的边分别是\(a，b，c\)，\(B=30°\)，\(A=45^°\)，\(b=2\)，则边\(a=\)\(\underline{\quad \quad}\).
\((2)\)已知两边和其中—边的对角，求其他两个角及另一边.
\({\color{Red}{Eg}}\) 在\(△ABC\)，内角\(A ,B ,C\)所对的边分别是\(a，b，c\)，\(A=60°\),\(c=\sqrt{2}\)，\(a=\sqrt{3}\)，则角\(C=\)\(\underline{\quad \quad}\).
(三角形中有一组对边和对角就可考虑正弦定理)
 

\(5\) 三角形解的个数问题
已知两边\(a、b\)和其中一边的对角\(A\)，不能确定三角形的形状，此时三角形解可能是无解、一解、两解，要分类讨论.

\({\color{Red}{Eg}}\) 求满足\(a=5\)，\(b=4\) ,\(A=60°\)的三角形\(△ABC\)个数.
方法1 利用正弦定理求解
由正弦定理可得：\(\dfrac{5}{\sin 60^{\circ}}=\dfrac{4}{\sin B}\)，
则\(\sin B=\dfrac{2 \sqrt{3}}{5}\)，
\(∵a>b\)，且\(A\)为锐角，
\(∴B\)有一解，故三角形只有一解；
方法2 图像法

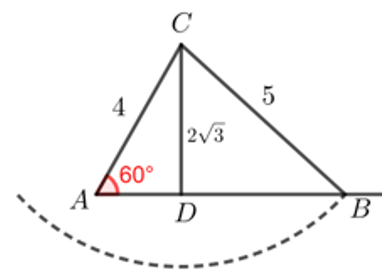
先做出角\(∠CAB=60^∘\) , 过点\(C\)作\(CD⊥BC\) , 此时可知\(C D=2 \sqrt{3}<5\)，以\(C\)为圆心，\(5\)为半径画个圆弧，由于\(b=4<a=5\)，显然圆弧与射线\(AB\)交于一个点，如图可知满足题意的三角形只有一个！
 

面积公式

\[S_{\triangle A B C}=\dfrac{1}{2} a b \sin C=\dfrac{1}{2} b c \sin A=\dfrac{1}{2} a c \sin B \]

 

余弦定理

\(1\) 余弦定理
\(\begin{aligned} &a^{2}=b^{2}+c^{2}-2 b c \cos A \\ &b^{2}=a^{2}+c^{2}-2 a \cos B \\ &c^{2}=a^{2}+b^{2}-2 a b \cos C \end{aligned}\)
 

\(2\) 变形
\(\begin{aligned} &\cos A=\dfrac{b^{2}+c^{2}-a^{2}}{2 b c} \\ &\cos B=\dfrac{a^{2}+c^{2}-b^{2}}{2 a c} \\ &\cos C=\dfrac{a^{2}+b^{2}-c^{2}}{2 a b} \end{aligned}\)
 

\(3\) 利用余弦定理可以解决下列两类三角形的问题
\((1)\) 已知三边，可求三个角；
\({\color{Red}{Eg}}\) 在\(△ABC\)中，若\(a=4\) ,\(b=3\) ,\(c=\sqrt{13},\)，则角\(C=\) .
\((2)\) 已知两边和一角，求第三边和其他两个角.
\({\color{Red}{Eg}}\) 在\(△ABC\)中，\(A=30°\) ,\(b=\sqrt{3}\) ,\(c=1\)，则\(a=\) .(角\(A\)为两边的夹角)
在\(△ABC\)中，\(A=30°\)，\(b=3 \sqrt{3},\)，\(a=3\), 则边\(c=\) . (角\(A\)不为两边的夹角)
 

\(4\) 三角形类型的判断
\(\begin{aligned} &\angle A=\dfrac{\pi}{2} \Rightarrow b^{2}+c^{2}=a^{2} ; \\ &\angle A>\dfrac{\pi}{2} \Rightarrow \cos A=\dfrac{b^{2}+c^{2}-a^{2}}{2 b c}<0 \Rightarrow b^{2}+c^{2}<a^{2} ; \\ &\angle A<\dfrac{\pi}{2} \Rightarrow \cos A=\dfrac{b^{2}+c^{2}-a^{2}}{2 b c}>0 \Rightarrow b^{2}+c^{2}>a^{2} . \end{aligned}\)
 

5 射影定理
\(\begin{aligned} &a=c \cdot \cos B+b \cdot \cos C \\ &b=a \cdot \cos C+c \cdot \cos A \\ &c=b \cdot \cos A+a \cdot \cos B \end{aligned}\)

 

经典例题

【题型一】正弦定理、余弦定理解单个三角形

【典题1】在\(△ABC\)中，角\(A、B、C\)的对边分别是\(a、b、c\)，若\(a=2\)，\(b=2 \sqrt{2}\)，且三角形有两解，则角\(A\)的取值范围是\(\underline{\quad \quad}\).
【解析】 \({\color{Red}{方法1}}\) \(∵a<b\)，\(∴A<B\)，
\(∴A\)为锐角，
\(\because \dfrac{\sin B}{\sin A}=\dfrac{b}{a}=\sqrt{2}\)，\(\therefore \sin B=\sqrt{2} \sin A<1 \Rightarrow \sin A<\dfrac{\sqrt{2}}{2}\)
\(\therefore 0<A<\dfrac{\pi}{4}\).
\({\color{Red}{方法2 几何法}}\)

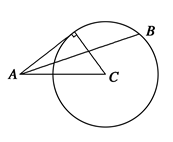
如图，\(A C=2 \sqrt{2}\)，以\(C\)为圆心\(2\)为半径作\(⊙C\)，则\(⊙C\)上任一点(\(⊙C\)与直线\(AC\)交点除外)可为点\(B\)构成\(△ABC\)，当\(AB\)与\(⊙C\)相切时，\(AB=2\)，\(\angle B A C=\dfrac{\pi}{4}\)；当\(AB\)与\(⊙C\)相交时，\(\angle B A C<\dfrac{\pi}{4}\)，因为三角形有两解，所以直线\(AB\)与\(⊙C\)应相交，\(\therefore 0<\angle B A C<\dfrac{\pi}{4}\).
【点拨】方法二想法与用\(bsinA<a<b\)(三角形有\(2\)个解可得)这个结论一致的，但不太赞成学习数学去套结论解题，应理解结论的推导方法.
 

【典题2】在\(△ABC\)中，角\(A ,B ,C\)的对边分别是\(a ,b ,c\)，且面积为\(S\)，若\(b \cos C+c \cos B=2 a \cos A\)，\(S=\dfrac{1}{4}\left(b^{2}+a^{2}-c^{2}\right)\)，则角\(B\)等于\(\underline{\quad \quad}\) .
【解析】 \({\color{Red}{方法1}}\) \(\because b \cos C+c \cos B=2 a \cos A\)，
由正弦定理可得\(\sin B \cos C+\sin C \cos B=2 \sin A \cos A\)，
\({\color{Red}{(把边化为角)}}\)
即\(\sin (B+C)=2 \sin A \cos A \Rightarrow \sin A=2 \sin A \cos A\)，
\({\color{Red}{(\sin (B+C)=\sin A)}}\)
\(∵\sin A≠0\)，\(\therefore \cos A=\dfrac{1}{2}\)，故\(A=\dfrac{1}{3} \pi\)，
\(∵S=\dfrac{1}{4}\left(b^{2}+a^{2}-c^{2}\right)\)，
\(\therefore \dfrac{1}{2} a b \sin C=\dfrac{1}{4} \times 2 a b \times \cos C\)，
\(∴\sin C=\cos C\)，\(\therefore C=\dfrac{\pi}{4}\)，
\(\therefore B=\dfrac{5 \pi}{12}\)．
\({\color{Red}{方法2}}\) \(∵b\cos C+c\cos B=2a\cos A\)
由余弦定理可得\(b \cdot \dfrac{a^{2}+b^{2}-c^{2}}{2 a b}+c \cdot \dfrac{a^{2}+c^{2}-b^{2}}{2 a c}=2 a \cdot \dfrac{b^{2}+c^{2}-a^{2}}{2 b c}\) (把角化边)
化简得\(bc=b^2+c^2-a^2\)
\(\therefore \cos A=\dfrac{1}{2}\)，故\(A=\dfrac{1}{3} \pi\)
接着同方法\(1\)
【点拨】
① 对于一有角有边的等式，可利用正弦定理或余弦定理化简为只含角或只含边的等式；
② 在三角形中\(\sin⁡(A+B)=\sin C\)，\(\cos⁡(A+B)=-\cos C\).
 

【典题3】 \(△ABC\)的内角\(A、B、C\)的对边分别为\(a、b、c\)，若\(c=2\)，\(\angle C=\dfrac{\pi}{3}\)，且\(\sin C+\sin(B-A)-2\sin2A=0\)，则下列选项不一定成立的是(　　)
A．\(b=2a\)
B．\(△ABC\)的周长为\(2+2 \sqrt{3}\)
C．\(△ABC\)的面积为\(\dfrac{2 \sqrt{3}}{3}\)
D．\(△ABC\)的外接圆半径为\(\dfrac{2 \sqrt{3}}{3}\)
【解析】 \(∵\sin C+\sin(B-A)-2\sin2A=0\)，
\(∴\sin(A+B)+\sin(B-A)-2\sin2A=0\)，
化简得\(\cos A(\sin B-2\sin A)=0\)，
\(∴\cos A=0\)或\(\sin B-2\sin A=0\)，
\((1)\)当\(\cos A=0\)，\(A=\dfrac{\pi}{2}\)时，
由\(\angle C=\dfrac{\pi}{3}\)得\(B=\dfrac{\pi}{6}\)，
\(∵c=2\) ，\(\therefore b=\dfrac{2 \sqrt{3}}{3}\)，\(a=\dfrac{4 \sqrt{3}}{3}\)；
\((2)\)当\(\sin B-2\sin A=0\)时，
由正弦定理得\(b=2a\)，
\(∵c=2\) ,\(\angle C=\dfrac{\pi}{3}\)，
\(∴\)由余弦定理得\(c^{2}=a^{2}+b^{2}-2 a b \cos C\)，
则\(4=a^{2}+4 a^{2}-2 a \times 2 a \times \dfrac{1}{2}\)，
解得\(a=\dfrac{2 \sqrt{3}}{3}\)，则\(b=\dfrac{4 \sqrt{3}}{3}\)，
此时满足\(b^2=a^2+c^2\)，即\(B=\dfrac{\pi}{2}\)，
对于\(A\)，当\(A=\dfrac{\pi}{2}\)时，\(a=2b\)，故\(A\)错误；
对于\(B\)，当\(A=\dfrac{\pi}{2}\)或\(B=\dfrac{\pi}{2}\)时，\(△ABC\)的周长为\(a+b+c=2+2 \sqrt{3}\)，故\(B\)正确；
对于\(C\)，当\(B=\dfrac{\pi}{2}\)时，\(△ABC\)的面积\(S=\dfrac{1}{2} a c=\dfrac{2 \sqrt{3}}{3}\)，
当\(A=\dfrac{\pi}{2}\)时，\(S=\dfrac{1}{2} b c=\dfrac{2 \sqrt{3}}{3}\)，故\(C\)正确；
对于\(D\)，当\(A=\dfrac{\pi}{2}\)或\(B=\dfrac{\pi}{2}\)时，由正弦定理得\(2 R=\dfrac{c}{\sin C}=\dfrac{4 \sqrt{3}}{3}\)，得\(R=\dfrac{2 \sqrt{3}}{3}\)，故\(D\)正确，
综上可得，命题正确的\(BCD\)，错误的为\(A\).故选：\(A\)．
 

巩固练习

1(★)在\(△ABC\)中，\(A B=\sqrt{2}\)，\(B C=\sqrt{3}\)，\(A=60^{\circ}\)则角\(C\)的值为\(\underline{\quad \quad}\)．
 

2(★)在\(△ABC\)中，内角\(A，B，C\)所对的边分别为\(a，b，c\)．若\(a=3\)，\(A=30°\)，\(b=3 \sqrt{3}\)，则\(c\)值为\(\underline{\quad \quad}\)．
 

3(★)在\(△ABC\)中，若\(\sin A: \sin B: \sin C=2: \sqrt{7}: 3\)，则\(△ABC\)的最大内角与最小内角的和为\(\underline{\quad \quad}\)．
 

4(★)【多选题】已知\(△ABC\)的内角\(A，B，C\)所对的边分别为\(a，b，c\)，根据下列条件解三角形，有两解的是(　　)
A．\(a=\sqrt{2}, b=2, B=120^{\circ}\)
B．\(a=2, b=\sqrt{3}, B=45^{\circ}\)
C．\(b=3, c=\sqrt{3}, B=60^{\circ}\)
D．\(a=2 \sqrt{3}, b=\sqrt{10}, B=60^{\circ}\)
 

5(★★)【多选题】下列命题中，正确的是(　　)
A．在\(△ABC\)中，\(A>B\)，则\(\sin A>\sin B\)
B．在锐角\(△ABC\)中，不等式\(\sin A>\cos B\)恒成立
C．在\(△ABC\)中，若\(a\cos A=b\cos B\)，则\(△ABC\)必是等腰直角三角形
D．在\(△ABC\)中，若\(B=60°\)，\(b^2=ac\)，则\(△ABC\)必是等边三角形
 

6(★★) 【多选题】在\(△ABC\)中，已知\((a+b):(c+a):(b+c)=6:5:4\)，给出下列结论中正确结论是(　　)
A．由已知条件，这个三角形被唯一确定
B．\(△ABC\)一定是钝三角形
C．\(\sin A:\sin B:\sin C=7:5:3\)
D．若\(b+c=8\)，则\(△ABC\)的面积是\(\dfrac{15 \sqrt{3}}{2}\)
 

7(★★) 在\(△ABC\)中，角\(A，B，C\)所对的边分别为\(a，b，c\)，若\(a^2+c^2-b^2+\)\(2bc\cos A-2c=0\)，\(c\cdot cosA=b(1-\cos C)\)，且\(C=\dfrac{2 \pi}{3}\)，则\(c=\)\(\underline{\quad \quad}\)；\(△ABC\)的面积\(S=\)\(\underline{\quad \quad}\)．
 

8(★★★)已知\(△ABC\)的内角\(A，B，C\)所对的边分别为\(a，b，c\)．且\(a\sin(A+B)\)\(=c\sin \dfrac{B+C}{2}\)．
(1)求\(A\)；
(2)若\(△ABC\)的面积为\(\sqrt{3}\)，周长为\(8\)，求\(a\)．
 

参考答案

1. \(\dfrac{\pi}{4}\)
2. \(3\)或\(6\)
3. \(\dfrac{2 \pi}{3}\)
4. \(BD\)
5. \(ABD\)
6. \(BC\)
7. \(1\)，\(\dfrac{\sqrt{3}}{12}\)
8. \(\text { (1) } A=\dfrac{\pi}{3} \quad \text { (2) } a=\dfrac{13}{4}\)
    

【题型二】多个三角形问题

【典题1】 在\(△ABC\)中，\(D\)是\(AB\)边上一点，\(AD=2DB\)，\(DC⊥AC\)，\(D C=\sqrt{3}\)，\(B C=\sqrt{7}\)，则\(AB=\)\(\underline{\quad \quad}\)．
【解析】如图，

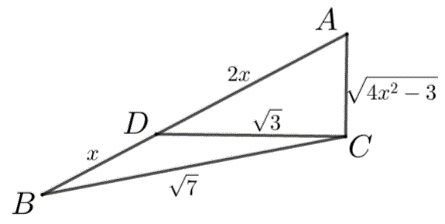
设\(BD=x\)，则\(AD=2x\) \({\color{Red}{(引入变量)}}\)
在\(Rt△ACD\)中，可得\(\cos A=\dfrac{\sqrt{4 x^{2}-3}}{2 x}\)，
在\(Rt△ABC\)中，由余弦定理可得
\(7=9 x^{2}+\left(4 x^{2}-3\right)-2 \cdot 3 x \cdot \sqrt{4 x^{2}-3} \cos A\)
\(\therefore 7=13 x^{2}-3-6 x \cdot \sqrt{4 x^{2}-3} \times \dfrac{\sqrt{4 x^{2}-3}}{2 x}\)
即\(7=6+x^2\)，解得\(x=1\)，
\(∴AB=3\)．
【点拨】
① 题目中出现类似\(AD=2DB\)的倍数关系，可设未知数(比如设\(BD=x\));
② 本题其实是对于同一角\(A\)在\(△ACD\)和\(△ABC\)共用了两次余弦定理，得到了一条\(x\)的方程最终求解成功.另一思路：\(\angle B D C+\angle A D C=\pi \Rightarrow \cos \angle B D C=-\cos \angle A D C\Rightarrow \dfrac{x^{2}+3-7}{2 \sqrt{3} x}=-\dfrac{\sqrt{3}}{2 x}\) , 解得\(x=1\).利用“同一角、邻补角互补，对角互补”等，在两个三角形里用正弦或余弦定理建立方程求解，这是在多三角形题目中常用技巧.
 

【典题2】 在平面四边形\(ABCD\)中，\(\angle A=\angle B=\angle C=75^{\circ}\)，\(BC=2\)，则\(AB\)的取值范围是\(\underline{\quad \quad}\)．
【解析】 \({\color{Red}{方法1}}\) 如图所示，延长\(BA ,CD\)交于点\(E\)，

则在\(△ADE\)中，\(∠DAE=105°\)，\(∠E=30°\)，\(∠ADE=45°\)，
\({\color{Red}{(在△ADE三个内角都已知，故三边成比例)}}\)
\(∴\)设\(A D=\dfrac{1}{2} x\)，\(A E=\dfrac{\sqrt{2}}{2} x\)，\(D E=\dfrac{\sqrt{6}+\sqrt{2}}{4} x\)，\(CD=m\)，
\(∵BC=2\)，\(△BCE\)是等腰三角形，
过点\(E\)作\(BC\)的垂线可得
\(\left(\dfrac{\sqrt{6}+\sqrt{2}}{4} x+m\right) \sin 15^{\circ}=1\)，即\(\dfrac{\sqrt{6}+\sqrt{2}}{4} x+m=\sqrt{6}+\sqrt{2}\)，
\(∵m>0\)，\(∴0＜x＜4\)，
\(∵BE=CE\) \(\therefore A B=\dfrac{\sqrt{6}+\sqrt{2}}{4} x+m-\dfrac{\sqrt{2}}{2} x=\sqrt{6}+\sqrt{2}-\dfrac{\sqrt{2}}{2} x\)
\(∴AB\)的取值范围是\((\sqrt{6}-\sqrt{2}, \sqrt{6}+\sqrt{2})\)．
\({\color{Red}{ 方法2 尺规作图法}}\)
如下图，作出底边\(BC=2\)的等腰三角形\(EBC\) ,\(B=C=75°\)，

与\(AB\)形成\(75°\)夹角的直线(图中虚线)在平面内移动，
分别交\(EB、EC\)于\(A、D\)，
则四边形\(ABCD\)即为满足题意的四边形；
当直线移动时，运用极限思想，
①直线接近点\(C\)时，\(AB\)趋近最小值，为\(\sqrt{6}-\sqrt{2}\)；
②直线接近点\(E\)时，\(AB\)趋近最大值，为\(\sqrt{6}+\sqrt{2}\)；
\(∴AB\)的取值范围是\((\sqrt{6}-\sqrt{2}, \sqrt{6}+\sqrt{2})\)．
【点拨】方法1通过辅助线得到两个三角形，引入变量再解三角形，有些复杂；
那方法2是怎么想到的呢？
下面我们试试运用“构图法”找思路

① 先思考满足“\(∠A=∠B=∠C=75°\)，\(BC=2\)”的四边形是否确定了呢？肯定不是，要不出题者让你求\(AB\)长度了. 我们试试“尺规作图”，如图一，先画出线段\(BC=2\)，再作角\(∠B=∠C=75^∘\)，那接着作\(∠A=75°\)，没其他条件限制，点\(A\)的位置无法确定，它可以移动；
② 当点\(A\)在射线\(BF\)上移动，如图二，易知A在线段\(BA_1\)上或在线段\(BE\)外是无法得到点\(D\)构造出四边形\(ABCD\)，故\(BA_1<BA<BE\)；
③ 在\(△BA_1 C\)和\(△BCE\)中利用正弦定理求出\(B A_{1}=\sqrt{6}-\sqrt{2}\)，\(B E=\sqrt{6}+\sqrt{2}\)，利用极限的位置就得到\(\sqrt{6}-\sqrt{2}<A B<\sqrt{6}+\sqrt{2}\).
这方法在几何中很常用，可确定题中哪些量是变量哪些是不变量，更便于寻找解题思路.
 

【典题3】 如图，等腰直角三角形\(ABC\)中，\(∠ACB=90°\)，\(AB=4\)，点\(P\)为\(△ABC\)内一点，
且\(\tan \angle P A B=\dfrac{1}{3}\)，\(\tan \angle P B A=\dfrac{1}{2}\)．
(1)求\(∠APB\)； \(\qquad \qquad\) (2)求\(PC\)．

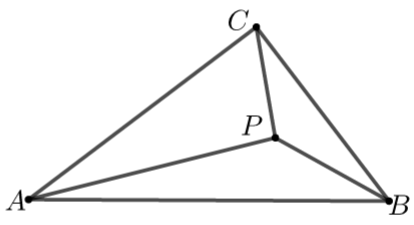
【解析】(1)设\(∠PAB=∠1\)，\(∠PBA=∠2\)，
由\(\tan \angle 1=\dfrac{1}{3}\)，\(\tan \angle 2=\dfrac{1}{2}\)
可知\(\sin \angle 1=\dfrac{\sqrt{10}}{10}\)，\(\cos \angle 1=\dfrac{3 \sqrt{10}}{10}\)，\(\sin \angle 2=\dfrac{\sqrt{5}}{5}\)，\(\cos \angle 2=\dfrac{2 \sqrt{5}}{5}\)．
\({\color{Red}{(\sin x、\cos x、\tan x三者知一得二)}}\)
\(\therefore \cos \angle A P B=-\cos (\angle 1+\angle 2)\)\(=\sin \angle 1 \sin \angle 2-\cos \angle 1 \cos \angle 2 =\dfrac{\sqrt{10}}{10} \times \dfrac{\sqrt{5}}{5}-\dfrac{3 \sqrt{10}}{10} \times \dfrac{2 \sqrt{5}}{5}=-\dfrac{\sqrt{2}}{2}\)．
\(\therefore \angle A P B=\dfrac{3 \pi}{4}\)．
(2)在\(△PAB\)中，利用正弦定理可得\(A P=\dfrac{A B \cdot \sin \angle 2}{\sin \angle A P B}=\dfrac{4 \sqrt{10}}{5}\)，
依题意易得\(\angle C A B=\dfrac{\pi}{4}\)，
\(A C=2 \sqrt{2}\)
\(\therefore \cos \angle P A C=\cos \left(\dfrac{\pi}{4}-\angle 1\right) =\dfrac{\sqrt{2}}{2}(\cos \angle 1+\sin \angle 1)=\dfrac{2 \sqrt{5}}{5}\)．
在\(△APC\)中，利用余弦定理得
\(P C^{2}=A P^{2}+A C^{2}-2 A P \cdot A C \cdot \cos \angle P A C=\dfrac{32}{5}+8-2 \times \dfrac{4 \sqrt{10}}{5} \times 2 \sqrt{2} \times \dfrac{2 \sqrt{5}}{5}=\dfrac{8}{5}\)．
\(\therefore P C=\dfrac{2 \sqrt{10}}{5}\)．
【点拨】
① 解题中要明确什么量是确定或不确定的，比如已知\(\tan \angle P A B=\dfrac{1}{3}\)，\(\tan \angle P B A=\dfrac{1}{2}\)意味着角\(∠PAB\)和\(∠PBA\)是确定的(只是具体多少度不知道)，再加上\(AB=4\)，由三角形的\(AAS\)型可知三角形\(PAB\)是确定了，那可求\(∠APB\)、\(AP\)，在等腰三角形\(ABC\)中\(AB=4\)，则\(△ABC\)确定，这可求边长\(AC\)、\(∠PAC\), 则\(△PAC\)确定 , 可求\(PC\). 这样解题中能够作到“心中有数”！
② 处理多个三角形问题，要大胆在各三角形中尝试用正弦余弦定理，利用综合法分析法进行推理分析！
 

巩固练习

1(★★) 已知\(△ABC\)的内角\(A，B，C\)所对的边分别为\(a，b，c\)，且\(a=2b\)，\(△ABC\)的面积为\(4\sin∠ACB\)，\(AB\)边上的中线\(CD\)长为\(\sqrt{6}\)，则\(△ABC\)的周长为\(\underline{\quad \quad}\)．
 

2(★★) 在\(△ABC\)中，内角\(A，B，C\)所对的边分别为\(a，b，c\)．已知\(c=2\)，\(b=1\)，\(\cos C=\dfrac{1}{4}\)．则\(△ABC\)的中线\(AD\)的长为\(\underline{\quad \quad}\)．
 

3(★★) 已知\(△ABC\)中，\(AB=3\)，\(BC=5\)，\(D\)为线段\(AC\)上一点，\(AB⊥BD\)，\(\dfrac{A D}{C D}=\dfrac{3}{4}\)，则\(AC=\)\(\underline{\quad \quad}\)，\(△ABC\)的面积是\(\underline{\quad \quad}\)．
 

4(★★★) 在\(△ABC\)中，\(∠C=90°\)，\(M\)是\(BC\)边上一点，且满足\(\overrightarrow{C M}=2 \overrightarrow{M B}\)，若\(\sin \angle B A M=\dfrac{1}{5}\)，则\(\sin∠BAC=\)\(\underline{\quad \quad}\)．
 

5(★★★)已知圆内接四边形\(ABCD\)，其中\(AB=6\)，\(BC=3\)，\(CD=4\)，\(AD=5\)，则\(\dfrac{2}{\sin A}+\dfrac{2}{\sin B}=\)\(\underline{\quad \quad}\)．
 

6(★★★) 如图，在梯形\(ABCD\)中，\(AB∥CD\)，\(∠A=60°\)，\(M\)为\(AD\)上一点，\(AM=2MD=2\)，\(∠BMC=60°\)．
(1)若\(△MCD\)为等腰三角形，求\(BC\)；
(2)设\(∠DCM=θ\)，若\(MB=4MC\)，求\(\tanθ\)．
 
 
 

参考答案

1. \(10\)
2. \(\dfrac{\sqrt{6}}{2}\)
3. \(\sqrt{58}, \dfrac{9}{2}\)
4. \(\dfrac{\sqrt{15}}{5}\)
5. \(\dfrac{4 \sqrt{10}}{3}\)
6. \((1) BC=3 \quad \text { (2) } \tan \theta=\dfrac{\sqrt{3}}{2}\)
    

【题型三】三角形最值问题

【典题1】 锐角三角形\(ABC\)的内角\(A ,B ,C\)的对边分别为\(a ,b ,c\)，已知\(2 \operatorname{asin} C=\sqrt{3} c\)，\(a=1\)，则\(△ABC\)周长的范围为\(\underline{\quad \quad}\).
【解析】 \(∵2 a\sin C=\sqrt{3} c\)，
\(∴\)由正弦定理得\(2 \sin A \sin C=\sqrt{3} \sin C\)，
\(∵0<C<π\)，\(∴\sin C≠0\)．\(\therefore \sin A=\dfrac{\sqrt{3}}{2}\)
\(∵\)三角形\(ABC\)是锐角三角形，\(\therefore A=\dfrac{\pi}{3}\)
\({\color{Red}{(确定A与a，隐圆模型)}}\)
\({\color{Red}{方法1}}\) 由正弦定理得\(\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=\dfrac{a}{\sin A}=\dfrac{2}{\sqrt{3}}\)
则\(b+c=\dfrac{2}{\sqrt{3}}(\sin B+\sin C)\)\(=\dfrac{2}{\sqrt{3}}\left[\sin B+\sin \left(\dfrac{2 \pi}{3}-B\right)\right]=2 \sin \left(B+\dfrac{\pi}{6}\right)\)
\(∵\)锐角三角形\(ABC\) \(\therefore \dfrac{\pi}{6}<B<\dfrac{\pi}{2}\)，
则\(\sqrt{3}<2 \sin \left(B+\dfrac{\pi}{6}\right) \leq 2\)，
即\(\sqrt{3}<b+c \leq 2\) (当\(B=\dfrac{\pi}{3}\)时取到等号)
\(\therefore 1+\sqrt{3}<a+b+c \leq 3,\)，
\(∴△ABC\)周长的范围为\((1+\sqrt{3}, 3]\)．
\({\color{Red}{方法2}}\) 由余弦定理得\(a^2=b^2+c^2-2bc\cos A\)，
\(∴1=(b+c)^2-3bc\)，\(\therefore b c=\dfrac{(b+c)^{2}-1}{3}\)，显然\(\dfrac{(b+c)^{2}-1}{3}>0 \Rightarrow b+c>\sqrt{3}\)
\(\because b c \leq \dfrac{(b+c)^{2}}{4}\)，\(\therefore \dfrac{(b+c)^{2}-1}{3} \leq \dfrac{(b+c)^{2}}{4}\)
\(∴b+c≤2\)，当且仅当\(b=c=1\)时等号成立，
\(\therefore \sqrt{3}<b+c \leq 2\)，
\(\therefore 1+\sqrt{3}<a+b+c \leq 3\)，
即\(△ABC\)周长的范围为\((1+\sqrt{3}, 3]\)．
【点拨】
① 方法1把边的最值问题转化为三角函数最值处理，注意角度的范围；
② 方法2把\(b+c\)看成一个整体，利用基本不等式求最值.
③ 本题属于隐圆问题，\(△ABC\)的外接圆是确定的，由图也可得到\(△ABC\)周长的范围为\((1+\sqrt{3}, 3]\)(但不够严谨).
 

【典题2】边长为\(1\)的正方形\(ABCD\)的边\(BC\)上有一点\(P\)，边\(CD\)上有一点\(Q\)，满足\(△CPQ\)的周长为\(2\)．
(1)求\(∠QAP\)的大小；
(2)求\(△APQ\)面积的最小值．

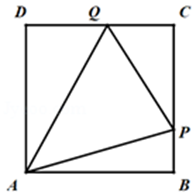
【解析】\({\color{Red}{方法1 变量法}}\)
(1)
\({\color{Red}{(分析 由△CPQ的周长为2和勾股定理可知CP,CQ,PQ三线关系，而S_{\triangle A P Q}=\dfrac{1}{2} A Q \cdot A P \sin \angle Q A P，故可引入变量表示各线段再进行求解.)}}\)
设\(∠PAB=α\)，\(∠DAQ=β\)，
\({\color{Red}{(引入角度变量较好，还有可引入其他变量么？)}}\)
则\(PB=\tanα\)，\(QD=\tanβ\)，\(PC=1-\tanα\)，\(QC=1-\tanβ\)，
\(∵△CPQ\)的周长为\(2\)，\(∴PQ=2-PC-CQ=\tanα+\tanβ\)
由勾股定理可得\((1-\tanα)^2+(1-\tanβ)^2=(\tanα+\tanβ)^2\)
展开整理可得\(2-2\tanα-2\tanβ=2\tanα \cdot \tanβ\)，
变形可得\(\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}=1\)，即\(\tan(α+β)=1\)，
\(∵α+β\)为锐角，\(\therefore \alpha+\beta=\dfrac{\pi}{4}\)，\(\therefore \angle Q A P=\dfrac{\pi}{2}-\dfrac{\pi}{4}=\dfrac{\pi}{4}\).
(2)\(S_{\triangle A P Q}=\dfrac{1}{2} A Q \cdot A P \cdot \sin \dfrac{\pi}{4}=\dfrac{1}{2 \sqrt{2} \cos \alpha \cdot \cos \beta}\)
又\(2 \sqrt{2} \cos \alpha \cdot \cos \beta=2 \sqrt{2} \cos \alpha \cdot \cos \left(\dfrac{\pi}{4}-\alpha\right)\)\(=2 \cos ^{2} \alpha+2 \cos \alpha \cdot \sin \alpha\)
\(=1+\cos 2 \alpha+\sin 2 \alpha=1+\sqrt{2} \sin \left(\dfrac{\pi}{4}+2 \alpha\right)\)，
\(\therefore 2 \sqrt{2} \cos \alpha \cdot \cos \beta=1+\sqrt{2} \sin \left(\dfrac{\pi}{4}+2 \alpha\right) \leq 1+\sqrt{2}\)， 当\(\alpha=\dfrac{\pi}{8}\)时取到等号，
\(\therefore \dfrac{1}{2 \sqrt{2} \cos \alpha \cdot \cos \beta} \geq \sqrt{2}-1\)
故\(S_{\triangle A P Q}\)最小值为\(\sqrt{2}-1\)．
\({\color{Red}{方法2 坐标系法}}\)
(1)如图，以点\(A\)为原点，\(AB\)为\(x\)轴，\(AD\)为\(y\)轴建立平面直角坐标系

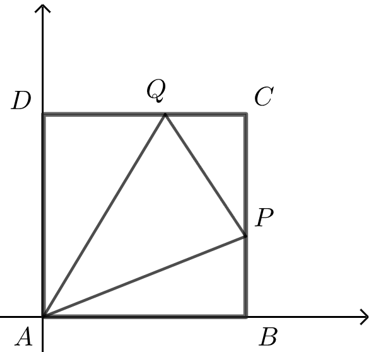
则\(A(0 ,0) ,B(1 ,0)\), 可设\(P(1 ,m) ,Q(n ,1)\), 其中\(0<m ,n<1\),
\({\color{Red}{ (相当引入线段变量)}}\)
则\(P Q=\sqrt{(1-n)^{2}+(1-m)^{2}}\)
\(∵△CPQ\)的周长为\(2\)，\(∴ PQ=2-PC-CQ=2-(1-m)-(1-n)=m+n\)
\(∴Rt∆CPQ\)中由勾股定理得\((m+n)^2=(1-n)^2+(1-m)^2\)，化简得\(m+n=1-mn\)，
\(\therefore \cos \angle Q A P=\dfrac{\overrightarrow{A Q} \cdot \overrightarrow{A P}}{|\overrightarrow{A Q}| \cdot|\overrightarrow{A P}|}=\dfrac{m+n}{\sqrt{1+n^{2}} \cdot \sqrt{1+m^{2}}}\)\(=\dfrac{m+n}{\sqrt{1+n^{2}+m^{2}+n^{2} m^{2}}}=\dfrac{m+n}{\sqrt{2(1-m m)^{2}}}=\dfrac{\sqrt{2}}{2}\)
\({\color{Red}{(数量积处理)}}\)
\({\color{Red}{(也可以在∆QAP中用余弦定理处理)}}\)
\(\therefore \angle Q A P=\dfrac{\pi}{4}\)；
(2)\(S_{\triangle A P Q}=S_{\text {正方形 } A B C D}-S_{\triangle A B P}-S_{\triangle A D Q}-S_{\triangle C P Q}\)
\(=1-\dfrac{m}{2}-\dfrac{n}{2}-\dfrac{(1-m)(1-n)}{2}=\dfrac{1-m n}{2}\)
\({\color{Red}{(涉及面积，割补法也是很常见的)}}\)
由(1)可知\(m+n=1-mn\)，
\(∵m ,n>0\) \(\therefore m+n \geq 2 \sqrt{m n}\)
即\(1-m n \geq 2 \sqrt{m n}\) ，
解得\(0<m n \leq 3-2 \sqrt{2}\)
(当\(m=n=\sqrt{2}-1\)时取到“=”)
\(\therefore S_{\triangle A P Q}=\dfrac{1-m n}{2} \geq \sqrt{2}-1\)
\(\therefore S_{\triangle A P Q}\)最小值为$ \sqrt{2}-1$．
【点拨】

① 本题还有一种方法，如图，延长\(PB\)到\(E\) , 使得\(BE=DQ\)，利用\(△APQ≅△APE\).

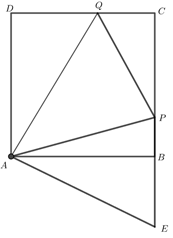
② 方法\(1\)是引入角度变量，第二问用三角函数表示边长，面积最值最后转化为三角函数的最值问题(涉及到辅助角公式、二倍角公式等)；而方法2是引入线段变量，而建系的方式使得每个量都能通过点的坐标得到，使得解题思路更简洁些；
③ 涉及到三角形面积，求法有\(S=\dfrac{1}{2} \cdot \text { 底 } \cdot \text { 高 }\)、\(S=\dfrac{1}{2} a b \sin C\)、隔补法等.
 

巩固练习

1(★★) 设锐角\(△ABC\)的三内角\(A，B，C\)所对边的边长分别为\(a，b，c\)，且\(b=2\)，\(A=2B\)，则\(a\)的取值范围为 \(\underline{\quad \quad}\)．
 

2(★★★)在\(△ABC\)中，\(∠B=60°\)，\(b=\sqrt{3}\)，若\(c-2a≤m\)恒成立，则\(m\)的最小值为\(\underline{\quad \quad}\)．
 

3(★★★) 在\(△ABC\)中，\(a、b、c\)分别是角\(A、B、C\)的对边，若\(c\cdot \cos B+b\cos C=2a\cdot \cos A\)，\(M\)为\(BC\)的中点，且\(AM=1\)，则\(b+c\)的最大值是\(\underline{\quad \quad}\)．
 

4(★★★) 在\(△ABC\)中，角\(A ,B ,C\)的对边分别为\(a ,b ,c\)，若\((a+b)(\sin A－\sin B)=c(\sin C+\sin B)\)，\(b+c=4\)，则\(△ABC\)的面积的最大值为\(\underline{\quad \quad}\)．
 

5(★★★) 已知在\(△ABC\)中，\(\angle B A C=\dfrac{2 \pi}{3}\)，点\(P\)在边\(BC\)上，且\(AP⊥AB\)，\(A P=\sqrt{3}\)．
(1)若\(P C=\sqrt{7}\)，求\(PB\)．(2)求\(\dfrac{2}{P B}+\dfrac{1}{P C}\)的取值范围．
 
 
 

6(★★★) 如图，在四边形\(ABCD\)中，\(AD⊥AB\)，\(∠CAB=60°\)，\(∠BCD=120°\)，\(AC=2\)．
(1)若\(∠ABC=30°\)，求\(DC\)；
(2)记\(∠ABC=θ\)，当\(θ\)为何值时，\(△BCD\)的面积有最小值？求出最小值．
 
 
 

参考答案

1. \((2 \sqrt{2}, 2 \sqrt{3})\)
2. \(\sqrt{3}\)
3. \(\dfrac{4 \sqrt{3}}{3}\)
4. \(\sqrt{3}\)
5. \(\text { (1) } \sqrt{7}\) \(\text { (2) }\left(1, \dfrac{2 \sqrt{3}}{3}\right]\)
6. \(\text { (1) } C D=\dfrac{2 \sqrt{3}}{3}\) \((2)θ=75°\)时，\(S\)取最小值\(6-3 \sqrt{3}\)
    

【题型四】解三角形应用举例

【典题1】如图，一架飞机以\(600km/h\)的速度，沿方位角\(60°\)的航向从\(A\)地出发向\(B\)地飞行，飞行了\(36min\)后到达\(E\)地，飞机由于天气原因按命令改飞\(C\)地，已知\(A D=600 \sqrt{3} \mathrm{~km}\)，$CD=1200km $， \(BC=500km\)，且\(\angle A D C=30^{\circ}\)，\(\angle B C D=113^{\circ}\)．问收到命令时飞机应该沿什么航向飞行，此时\(E\)地离\(C\)地的距离是多少？(参考数据：\(\tan 37^{\circ}=\dfrac{3}{4}\))

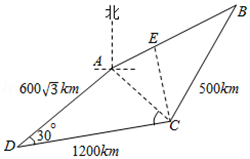
【解析】连接\(AC ,CE\)，在\(△ACD\)中由余弦定理得
\(A C^{2}=(600 \sqrt{3})^{2}+1200^{2}-2 \cdot 600 \sqrt{3} \cdot 1200 \cdot \dfrac{\sqrt{3}}{2}=360000\)
\(∴AC=600\)，
则\(CD^2=AD^2+AC^2\)，
即\(△ACD\)是直角三角形，且\(∠ACD=60°\)，
又\(∠BCD=113°\)，则\(∠ACB=53°\)，
\(∵\tan 37^{\circ}=\dfrac{3}{4}\)，\(\therefore \cos 53^{\circ}=\sin 37^{\circ}=\dfrac{3}{5}\)，\(\therefore \cos \angle A C B=\dfrac{3}{5}\)
在\(△ABC\)中，由余弦定理得\(A B^{2}=600^{2}+500^{2}-2 \cdot 600 \cdot 500 \cdot \dfrac{3}{5}=500^{2}\)
则\(AB=500\)，
又\(BC=500\)，则\(△ABC\)是等腰三角形，且\(∠BAC=53°\)，
由已知有\(A E=600 \cdot \dfrac{36}{60}=360\)，
在\(△ACE\)中，由余弦定理有\(C E=\sqrt{360^{2}+600^{2}-2 \cdot 360 \cdot 600 \cdot \dfrac{3}{5}}=480\)
又\(AC^2=AE^2+CE^2\)，则\(∠AEC=90°\)．
由飞机出发时的方位角为\(600\)，
则飞机由\(E\)地改飞\(C\)地的方位角为\(90°+60°=150°\)．
答：收到命令时飞机应该沿方位角\(150°\)的航向飞行，\(E\)地离\(C\)地\(480km\)．
【点拨】
① 在实际问题时，理解仰角、俯角(它是在铅锤面上所成的角)，方位角(它是在水平面上所成的角)；
② 方位角是相对于某点而言，在确定方位角时要弄清楚时哪一个点的方位角；
③ 处理实际问题时要根据题意把实际问题的图形进行简化，并在图形上标出有关的角或边，明确最后实际要求的量可转化为三角形的什么量，再思考正弦定理或余弦定理解三角形.
 

巩固练习

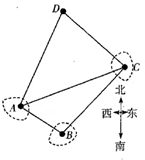
1(★★★) 如图，海平面某区域内有\(A，B，C\)三座小岛，岛\(C\)在\(A\)的北偏东\(70°\)方向，岛\(C\)在\(B\)的北偏东\(40°\)方向，岛\(B\)在\(A\)的南偏东\(65°\)方向，且\(A，B\)两岛间的距离为\(3\)海里．
(1)求\(B，C\)两岛间的距离；
(2)经测算海平面上一轮船\(D\)位于岛\(C\)的北偏西\(50°\)方向，且与岛\(C\)相距\(3 \sqrt{2}\)海里，求轮船在岛\(A\)的什么位置．(注：小岛与轮船视为一点)

 
 
 

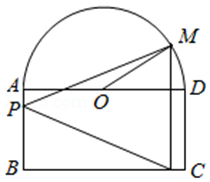
2(★★★) 如图，一个半圆和长方形组成的铁皮，长方形的边\(AD\)为半圆的直径，\(O\)为半圆的圆心，\(AB=1\) ,\(BC=2\)，现要将此铁皮剪出一个等腰三角形\(PMN\)，其底边\(MN⊥BC\)，点\(P\)在边\(AB\)上，设\(∠MOD=θ\)；
(1)若\(θ=30°\)，求三角形铁皮\(PMN\)的面积；
(2)求剪下的三角形铁皮\(PMN\)面积的最大值．

 
 
 
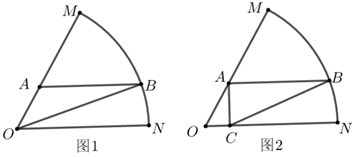
3(★★★★) 如图，已知扇形\(OMN\)是一个观光区的平面示意图，其中扇形半径为\(10\)米，\(\angle M O N=\dfrac{\pi}{3}\)，为了便于游客观光和旅游，提出以下两种设计方案：
(1)如图\(1\)，拟在观光区内规划一条三角形\(ABO\)形状的道路，道路的一个顶点B在弧\(MN\)上，另一顶点\(A\)在半径\(OM\)上，且\(AB∥ON\)，求\(△ABO\)周长的最大值；
(2)如图\(2\)，拟在观光区内规划一个三角形区域种植花卉，三角形花圃\(ABC\)的一个顶点\(B\)在弧\(MN\)上，另两个顶点\(A、C\)在半径\(OM、ON\)上，且\(AB∥ON\)，\(AC⊥ON\)，求花圃\(△ABC\)面积的最大值．

 
 
 

参考答案

1. \(\text { (1) } B C=3 \sqrt{2} \quad (2)\)北偏东\(25°\)
2. \(\text { (1) } \dfrac{6+3 \sqrt{3}}{8} \quad \text { (2) } \dfrac{3+2 \sqrt{2}}{4}\)
3. \(\text { (1) } \dfrac{20 \sqrt{3}}{3}+10 \quad \text { (2) } \dfrac{25 \sqrt{3}}{3}\)