三角函数综合习题解析

\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步拔高练习，难度4颗星！

【典题1】已知函数\(f(x)=\cos x \cos \left(x-\dfrac{\pi}{6}\right)+\sqrt{3} \sin ^{2} x-\dfrac{3 \sqrt{3}}{4}\)．
(1)求\(f(x)\)的最小正周期\(T\)；
(2)若\(f(x)+1+(-1)^n m>0\)对任意的\(x \in\left[-\dfrac{\pi}{4}, \dfrac{\pi}{4}\right]\)和\(n∈N^*\)恒成立，求实数\(m\)的取值范围．
【解析】(1)\(f(x)=\cos x \cos \left(x-\dfrac{\pi}{6}\right)+\sqrt{3} \sin ^{2} x-\dfrac{3 \sqrt{3}}{4}\)
\(\begin{aligned} &=\cos x\left(\dfrac{\sqrt{3}}{2} \cos x+\dfrac{1}{2} \sin x\right)+\sqrt{3} \dfrac{1-\cos 2 x}{2}-\dfrac{3 \sqrt{3}}{4} \\ &=\dfrac{\sqrt{3}}{2} \cos ^{2} x+\dfrac{1}{2} \sin x \cos x-\dfrac{\sqrt{3}}{2} \cos 2 x-\dfrac{\sqrt{3}}{4} \\ &=\dfrac{\sqrt{3}}{2} \cdot \dfrac{1+\cos 2 x}{2}+\dfrac{1}{4} \sin 2 x-\dfrac{\sqrt{3}}{2} \cos 2 x-\dfrac{\sqrt{3}}{4} \\ &=\dfrac{1}{4} \sin 2 x-\dfrac{\sqrt{3}}{4} \cos 2 x \\ &=\dfrac{1}{2} \sin \left(2 x-\dfrac{\pi}{3}\right) \end{aligned}\)
\({\color{Red}{(把函数化为f(x)=A\sin(ωx+φ)+B}}\)
\(f(x)\)的最小正周期\(T=\dfrac{2 \pi}{2}=\pi\)．
(2)由(1)知\(f(x)=\dfrac{1}{2} \sin \left(2 x-\dfrac{\pi}{3}\right)\)，
当\(y \in\left[-\dfrac{\pi}{4}, \dfrac{\pi}{4}\right]\)时，\(-\dfrac{5 \pi}{6} \leq 2 x-\dfrac{\pi}{3} \leq \dfrac{\pi}{6}\)，\(-\dfrac{1}{2} \leq \dfrac{1}{2} \sin \left(2 x-\dfrac{\pi}{3}\right) \leq \dfrac{1}{4},\)，
即\(-\dfrac{1}{2} \leq f(x) \leq \dfrac{1}{4}\)．
\({\color{Red}{ (问题中含(-1)^n，分n为偶数与n为奇数讨论) } }\)
①当\(n\)为偶数时，\(f(x)+1+(-1)^{n} m>0\Leftrightarrow f(x)+1+m>0 \Leftrightarrow m>-f(x)-1\)．
由题意，只需\(m>[-f(x)-1]_{\max }\)．
因为\([-f(x)-1]_{\max }=-\dfrac{1}{2}\)，所以\(m>-\dfrac{1}{2}\)．
②当\(n\)为奇数时，\(f(x)+1+(-1)^{n} m>0 \Leftrightarrow f(x)+1-m>0 \Leftrightarrow m<f(x)+1\)．
由题意，只需\(m<[f(x)+1]_{\min }\)．
因为当\(f(x)=-\dfrac{1}{2}\)时，\([f(x)+1]_{\min }=\dfrac{1}{2}\)，
所以\(m<\dfrac{1}{2}\)．
综上所述，实数\(m\)的取值范围是\(\left(-\dfrac{1}{2}, \dfrac{1}{2}\right)\)．
 

【典题2】已知函数\(f(x)=\cos2x+a\sin x+b(a<0)\)．
(1)若当\(x∈R\)时，\(f(x)\)的最大值为\(\dfrac{9}{8}\)，最小值为\(-2\)，求实数\(a ,b\)的值；
(2)若\(a=-2\)，\(b=1\)，设函数\(g(x)=m\sin x+2m\)，且当\(x \in\left[\dfrac{\pi}{6}, \dfrac{2 \pi}{3}\right]\)时，\(f(x)>g(x)\)恒成立，求实数\(m\)的取值范围．
【解析】(1)\(f(x)=\cos2x+a\sin x+b \)
\(=-2 \sin ^{2} x+a \sin x+b+1\)　
\(=-2\left(\sin x-\dfrac{a}{4}\right)^{2}+\dfrac{a^{2}}{8}+b+1\)，
(问题转化为二次函数动轴定区间最值问题)
因为\(-1≤\sin x≤1\)，(注意三角函数有界性)
所以当\(-1 \leq \dfrac{a}{4}<0\)时，\(f(x)_{\max }=\dfrac{a^{2}}{8}+b+1=\dfrac{9}{8}\)，\(f(x)_{\min }=a+b-1=2\)，
解得\(a=-1\)，\(b=0\)，
当\(\dfrac{a}{4}<-1\)时，\(f(x)_{\max }=-a+b-1=\dfrac{9}{8}\)，\(f(x)_{\min }=a+b-1=2\)，无解．
综上所述，\(a=-1\)，\(b=0\)．
(2) \(f(x)=-2 \sin ^{2} x-2 \sin x+2\)，
当\(x \in\left[\dfrac{\pi}{6}, \dfrac{2 \pi}{3}\right]\)时，\(-2 \sin ^{2} x-2 \sin x+2>m \sin x+2 m\)恒成立，
即\(m<-2 \cdot \dfrac{\sin ^{2} x+\sin x-1}{\sin x+2}\)，(分类参数法)
令\(u=\sin x+2\)，
\(\because x \in\left[\dfrac{\pi}{6}, \dfrac{2 \pi}{3}\right]\)，\(\therefore \dfrac{1}{2} \leq \sin x \leq 1\)，\(\therefore \dfrac{5}{2} \leq u \leq 3\)
则问题转化为\(m<-2 \cdot \dfrac{\sin ^{2} x+\sin x-1}{\sin x+2}=-2 \cdot \dfrac{(u-2)^{2}+(u-2)-1}{u}=6-2\left(u+\dfrac{1}{u}\right)\)恒成立
\(\because \dfrac{5}{2} \leq u \leq 3\)
\(\therefore 6-2\left(u+\dfrac{1}{u}\right) \geq-\dfrac{2}{3}\)(对勾函数的性质)
\(\therefore m<-\dfrac{2}{3}\)，
即实数\(m\)的取值范围是\(\left(-\infty,-\dfrac{2}{3}\right)\)．
【点拨】
① 处理三角函数问题注意其有界性；
② 恒成立问题注意分类参数法的运用；
③ 恒成立问题最终归根于最值问题，而常用的换元法能把问题“简化”；
④ 注意形如\(f(x)=\dfrac{a_{1} x^{2}+b_{1} x+c_{1}}{a_{2} x^{2}+b_{2} x+c_{2}}\)的最值模型，其中会用到换元法、分离常数法、基本不等式或对勾函数性质.
 

【典题3】已知函数\(h(x)=\sqrt{3} \sin ^{4} \dfrac{x}{2}+2 \sin \dfrac{x}{2} \cos \dfrac{x}{2}-\sqrt{3} \cos ^{4} \dfrac{x}{2}\)
(1)若先将函数\(h(x)\)图象上所有点的横坐标缩短到原来的\(\dfrac{1}{2}\)倍(纵坐标不变)，再将之向左平移\(\dfrac{\pi}{3}\)个单位，得到函数\(f(x)\)图象，求函数\(f(x)\)的解析式
(2)设\(g(x)=3-2 m+m \cos \left(2 x-\dfrac{\pi}{6}\right)(m \neq 0)\)，则是否存在实数\(m\)，满足对于任意\(x_{1} \in\left[0, \dfrac{\pi}{4}\right]\)，都存在\(x_{2} \in\left[0, \dfrac{\pi}{4}\right]\)，使得\(f(x_1)≥g(x_2)\)成立？如果存在，请求出实数\(m\)的取值范围；若不存在，请说明你的理由．
【解析】(1)\(h(x)=\sqrt{3} \sin ^{4} \dfrac{x}{2}+2 \sin \dfrac{x}{2} \cos \dfrac{x}{2}-\sqrt{3} \cos ^{4} \dfrac{x}{2}\)
\(\begin{aligned} &=\sqrt{3}\left(\sin ^{2} \dfrac{x}{2}+\cos ^{2} \dfrac{x}{2}\right)\left(\sin ^{2} \dfrac{x}{2}-\cos ^{2} \dfrac{x}{2}\right)+2 \sin \dfrac{x}{2} \cos \dfrac{x}{2} \\ &=-\sqrt{3} \cos x+\sin x \\ &=2 \sin \left(x-\dfrac{\pi}{3}\right) \end{aligned}\)
将函数\(h(x)\)图象上所有点的横坐标缩短到原来的\(\dfrac{1}{2}\)倍(纵坐标不变)，
得到\(h_{1}(x)=2 \sin \left(2 x-\dfrac{\pi}{3}\right)\)，
再向左平移\(\dfrac{\pi}{3}\)个单位，得到函数\(f(x)=2 \sin \left(2 x+\dfrac{\pi}{3}\right)\)，
所以函数\(f(x)\)的解析式为\(f(x)=2 \sin \left(2 x+\dfrac{\pi}{3}\right)\)．
(2) 若要满足题意，则只要\(f(x)_{\min } \geq g(x)_{\min }\)，(双变量恒成立问题)
\(\because x \in\left[0, \dfrac{\pi}{4}\right]\)，\(\therefore 2 x+\dfrac{\pi}{3} \in\left[\dfrac{\pi}{3}, \dfrac{5 \pi}{6}\right]\)，\(\therefore \sin \left(2 x+\dfrac{\pi}{3}\right) \in\left[\dfrac{1}{2}, 1\right]\)，即\(f(x)_{\min }=1\)；
\(\because x \in\left[0, \dfrac{\pi}{4}\right]\)，\(\therefore 2 x-\dfrac{\pi}{6} \in\left[-\dfrac{\pi}{6}, \dfrac{\pi}{3}\right]\)，\(\therefore \cos \left(2 x-\dfrac{\pi}{6}\right) \in\left[\dfrac{1}{2}, 1\right]\)，
\({\color{Red}{(要求g(x)_{\min }，需要分m>0和m<0讨论)}}\)
①当\(m>0\)时，\(\operatorname{mcos}\left(2 x_{2}-\dfrac{\pi}{6}\right) \in\left[\dfrac{m}{2}, m\right]\)，
即\(g(x)_{\min }=3-\dfrac{3 m}{2}\)，
则\(f(x)_{\min } \geq g(x)_{\min } \Rightarrow 1 \geq 3-\dfrac{3 m}{2}\)，
解得\(m \geq \dfrac{4}{3}\)，
②当\(m<0\)，\(\operatorname{mcos}\left(2 x_{2}-\dfrac{\pi}{6}\right) \in\left[m, \dfrac{m}{2}\right]\)，
即\(g(x)_{\min }=3-m\)，
则\(f(x)_{\min } \geq g(x)_{\min } \Rightarrow 1 \geq 3-m\)，
解得\(m≥2\)，与\(m<0\)矛盾，舍去．
综上所述，\(m\)的取值范围是\(\left[\dfrac{4}{3},+\infty\right)\)．
【点拨】双变量存在---恒成立问题
\((1)∀x_1∈D\)，\(∀x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{min}≥g(x)_{max}\)；
\((2)∀x_1∈D\)，\(∃x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{min}≥g(x)_{min}\)；
\((3)∃x_1∈D\)，\(∀x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{max}≥g(x)_{max}\)；
\((4)∃x_1∈D\)，\(∃x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{max}≥g(x)_{min}\).
 

【典题4】已知函数\(f(x)=A \sin (x+\varphi)\)\(\left(A>0, \varphi \in\left(0, \dfrac{\pi}{2}\right)\right)\)，\(y=f(x)\)的部分图象，如图所示，\(P、Q\)分别为该图象的最高点和最低点，点\(P\)的坐标为\(\left(\dfrac{\pi}{4}, A\right)\)，点\(R\)的坐标为\(\left(\dfrac{\pi}{4}, 0\right)\)，且\(\tan \angle P R Q=-\dfrac{\pi \sqrt{2}}{2}\)．
(1)求\(f(x)\)解析式；
(2)若方程\(\sin x \cos x+1=a f(x)(a \geq 1)\)在区间\(\left[0, \dfrac{3 \pi}{4}\right]\)内恰有一个根，求\(a\)的取值范围．

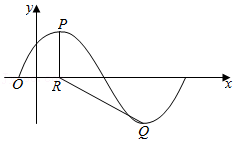
【解析】(1)过程略，\(f(x)=\sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)\)．
(2)方法一 方程\(\sin x \cos x+1=a \cdot \sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)(a \geq 1)\)
在区间\(\left[0, \dfrac{3 \pi}{4}\right]\)内恰有一个根\((*)\)，
显然\(\dfrac{3 \pi}{4}\)不是方程的根，
则问题\((*)\)等价于\(a=\dfrac{\sin x \cos x+1}{\sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)}=\dfrac{\sin x \cos x+1}{\sin x+\cos x}\)在\(\left[0, \dfrac{3 \pi}{4}\right)\)内恰有一个零点，(分离参数法)
等价于\(y=a\)与\(u(x)=\dfrac{\sin x \cos x+1}{\sin x+\cos x}\)在\(\left[0, \dfrac{3 \pi}{4}\right)\)内恰有一个交点，
设\(t=\sin x+\cos x=\sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)\)，
当\(x \in\left[0, \dfrac{3 \pi}{4}\right)\)时，\(t \in(0, \sqrt{2}]\)．
又\(\sin x \cos x=\dfrac{1}{2}\left[(\sin x+\cos x)^{2}-1\right]=\dfrac{1}{2}\left(t^{2}-1\right)\)
\({\color{Red}{(注意到\sin x+\cos x与\sin x \cos x的关系，利用换元法)}}\)
则\(\dfrac{\sin x \cos x+1}{\sin x+\cos x}=\dfrac{1}{2}\left(t+\dfrac{1}{t}\right), \quad t \in(0, \sqrt{2}]\)
令\(h(t)=\dfrac{1}{2}\left(t+\dfrac{1}{t}\right)\)，
由\(y=a\)与\(u(x)=\dfrac{\sin x \cos x+1}{\sin x+\cos x}\)在\(\left[0, \dfrac{3 \pi}{4}\right)\)内恰有一个交点
可知\(y=a\)与\(h(t)=\dfrac{1}{2}\left(t+\dfrac{1}{t}\right)\)在\((0, \sqrt{2}]\)内最多一个交点，
\({\color{Red}{(注意不能直接等价于y=h(t)在(0, \sqrt{2}]内恰有一个零点，u(x)是由h(t)与t(x)组成的复合函数)}}\)
易知\(h(t)=\dfrac{1}{2}\left(t+\dfrac{1}{t}\right)\)在\((0,1)\)上递减，在\((1, \sqrt{2}]\)递增，且\(h(1)=1\)，\(h(\sqrt{2})=\dfrac{3 \sqrt{2}}{4}\)\({\color{Red}{ (如图所示)}}\)

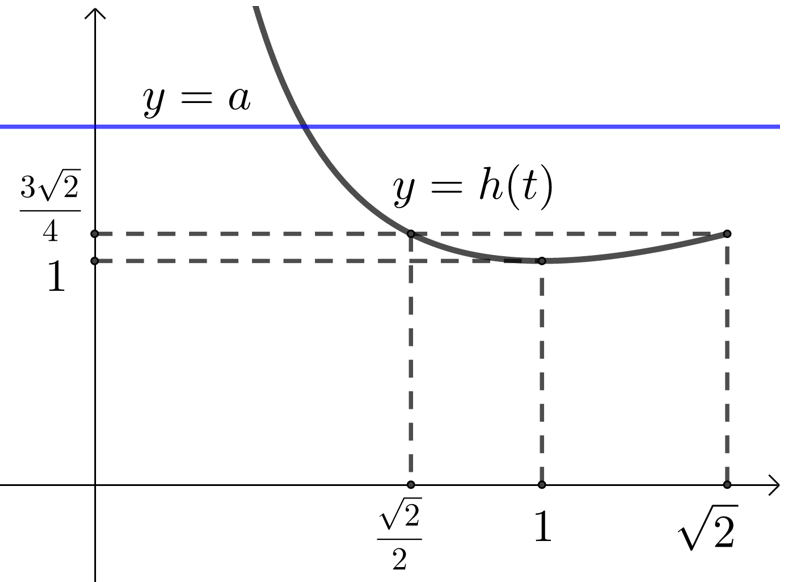
①当\(a=1\)时，此时\(t=1\)，
由\(1=\sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)\)在\(\left[0, \dfrac{3 \pi}{4}\right]\)内得\(x=0\)或\(x=\dfrac{\pi}{2}\)有两个解，不符合题意；(注意检验)
② 当\(a>1\)时，若要满足题意则需要\(a>\dfrac{3 \sqrt{2}}{4}\)，
此时\(0<t<\dfrac{\sqrt{2}}{2}\)，而\(y=t\)与函数\(y=\sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)\)在\(\left[0, \dfrac{3 \pi}{4}\right)\)内显然只有一个交点，
故\(a>\dfrac{3 \sqrt{2}}{4}\)满足题意，
综上，\(a\)的取值范围是\(\left(\dfrac{3 \sqrt{2}}{4},+\infty\right)\)．
方法二 设\(g(x)=a f(x)-\sin x \cos x-1\)\(=a(\sin x+\cos x)-\sin x \cos x-1\)，
方程\(\sin x \cos x+1=a f(x)(a \geq 1)\)在区间\(\left[0, \dfrac{3 \pi}{4}\right]\)内恰有一个根，
等价于函数g(x)在区间\(\left[0, \dfrac{3 \pi}{4}\right]\)内恰有一个零点．
\({\color{Red}{(方程与函数思想，对方程\sin x \cos x+1=a f(x)变形直接构造函数y=g(x))}}\)
设\(t=\sin x+\cos x=\sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)\)，当\(x \in\left[0, \dfrac{3 \pi}{4}\right]\)时，\(t \in[0, \sqrt{2}]\)．
又\(\sin x \cos x=\dfrac{1}{2}\left[(\sin x+\cos x)^{2}-1\right]=\dfrac{1}{2}\left(t^{2}-1\right)\)
\({\color{Red}{(注意到\sin x+\cos x与\sin x\cos x的关系，利用换元法)}}\)
则\(-\sin x \cos x+a(\sin x+\cos x)-1=-\dfrac{1}{2} t^{2}+a t-\dfrac{1}{2}，t \in[0, \sqrt{2}]\)
令\(h(t)=-\dfrac{1}{2} t^{2}+a t-\dfrac{1}{2}\)，由函数\(g(x)\)在\(\left[0, \dfrac{3 \pi}{4}\right]\)内恰有一个零点，
可知\(h(t)=-\dfrac{1}{2} t^{2}+a t-\dfrac{1}{2}\)在\([0, \sqrt{2}]\)内最多一个零点，
(注意不能直接等价于\(y=h(t)\)在\([0, \sqrt{2}]\)内恰有一个零点)
由于\(a≥1\)，函数\(y=h(t)\)判别式\(∆=a^2-1≥0\)，
①当\(Δ=0\)，得\(a=1\)时，此时零点为\(1\)，即\(t=1\)，
由\(1=\sqrt{2} \sin \left(x+\dfrac{\pi}{4}\right)\)在\(\left[0, \dfrac{3 \pi}{4}\right]\)内得\(x=0\)或\(x=\dfrac{\pi}{2}\)有两个解，不符合题意；(注意检验)
② 若\(Δ=a^2－1>0\)，即\(a>1\)时，
注意到\(h(0)=-\dfrac{1}{2}<0\)，函数开口向下，
要使\(h(t)=-\dfrac{1}{2} t^{2}+a t-\dfrac{1}{2}\)在\([0, \sqrt{2}]\)内恰有一个零点，
则\(h(\sqrt{2})>0\)，解得\(a>\dfrac{3 \sqrt{2}}{4}\)，
综上，\(a\)的取值范围是\(\left(\dfrac{3 \sqrt{2}}{4},+\infty\right)\)．
【点拨】
① 对于复合函数的零点问题，注意函数的构造方法与问题等价转化的严谨性；
② 方法二中要注意：对于二次函数，我们常考量：开口方向、对称轴、判别式、特殊点(常见的是一些定点)；二次函数零点分布问题，多结合函数图象进行思考！
 

【典题5】已知\(A\)是半径为\(2\)的半圆上的一点，\(BC\)是半圆的直径，\(PQRS\)为\(△ABC\)的内接正方形，记\(△ABC\)、正方形\(PQRS\)的面积分别为\(S_1\)，\(S_2\)，\(\angle A B C=\alpha\left(0<\alpha<\dfrac{\pi}{2}\right)\)．
(1)分别写出\(S_1 ,S_2\)关于\(α\)的函数；
(2)求\(\dfrac{S_{1}}{S_{2}}\) 的最小值．

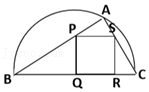
【解析】(1)因为\(BC\)是半圆的直径，所以\(AB⊥AC\)，
又\(BC=4\)，所以\(A B=4 \cos \alpha, A C=4 \sin \alpha\)，
所以\(S_{1}=\dfrac{1}{2} A B \cdot A C=\dfrac{1}{2} \times 4 \sin \alpha \times 4 \cos \alpha=4 \sin 2 \alpha\)，
设正方形的边长为\(x\)，则\(B P=\dfrac{x}{\sin \alpha}\)，\(A P=x \cos \alpha\)
(利用平几知识求解)
由\(BP+AP=AB\)，
得\(\dfrac{x}{\sin \alpha}+x \cos \alpha=4 \cos \alpha\)，
解得\(x=\dfrac{4 \sin \alpha \cos \alpha}{1+\sin \alpha \cos \alpha}=\dfrac{4 \sin 2 \alpha}{2+\sin 2 \alpha}\)，
所以\(S_{2}=x^{2}=\left(\dfrac{4 \sin 2 \alpha}{2+\sin 2 \alpha}\right)^{2}=\dfrac{16 \sin ^{2} 2 \alpha}{(2+\sin 2 \alpha)^{2}}\left(0<\alpha<\dfrac{\pi}{2}\right)\)．
(2)\(\dfrac{S_{1}}{S_{2}}=\dfrac{(2+\sin 2 \alpha)^{2}}{4 \sin 2 \alpha}=\dfrac{1}{\sin 2 \alpha}+\dfrac{1}{4} \sin 2 \alpha+1\)
令\(t=\sin2α\)，因为\(0<\alpha<\dfrac{\pi}{2}\)，所以\(0<2α<π\)，则\(t=\sin2α∈(0 ,1]\)，
所以\(\dfrac{S_{1}}{S_{2}}=\dfrac{1}{t}+\dfrac{t}{4}+1\)，
令\(g(t)=\dfrac{1}{t}+\dfrac{t}{4}+1(0<t \leq 1)\)，(对勾函数)
显然函数\(g(t)\)在\((0 ,1]\)上递减，
当\(t=1\)时，\(g(t)\)取得最小值\(g(1)=\dfrac{9}{4}\)，
此时\(\sin2α=1\)，解得\(\alpha=\dfrac{\pi}{4}\)．
所以\(\dfrac{s_{1}}{s_{2}}\) 的最小值为\(\dfrac{9}{4}\)．