5.7 函数y=Asin(ωx+φ)的图像和性质

\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学，so \quad easy！}}\)

必修第一册同步拔高练习，难度3颗星！

模块导图

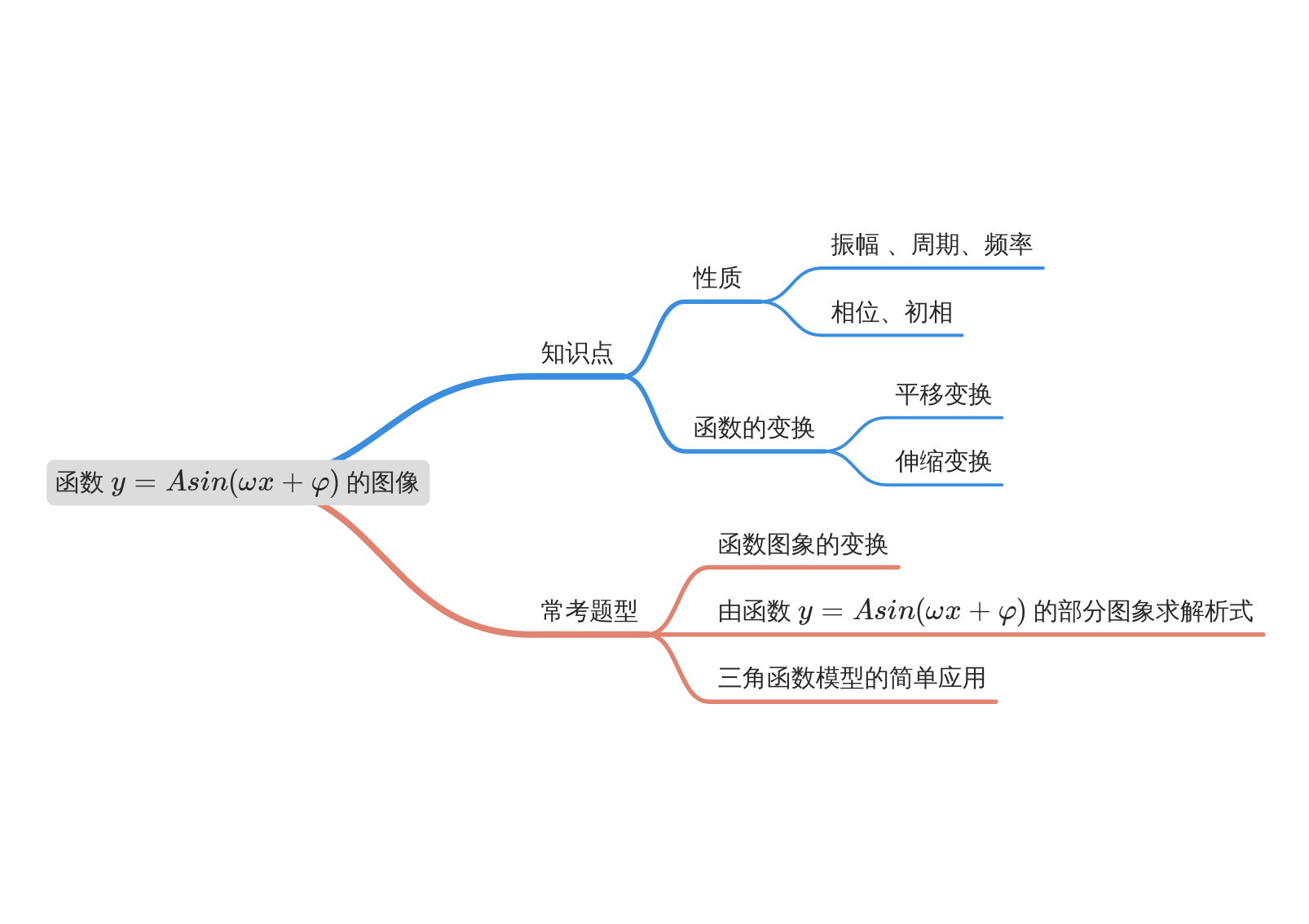
知识剖析

性质

\((1)\)简谐运动可用函数\(y=A \sin (\omega x+\varphi)\)，\(x∈[0,+∞)\)表示，
\(A\)是振幅，周期\(T=\dfrac{2 \pi}{\omega}\)，频率\(f=\dfrac{1}{T}=\dfrac{\omega}{2 \pi}\)，相位\(ωx+φ\)，初相\(φ\).
 

\((2)\) \(A,ω,φ\)对\(f(x)=A \sin (\omega x+\varphi)\)的影响
\(A\)影响函数\(y=f(x)\)的最值，\(ω\)影响周期，\(φ\)影响函数水平位置.

 

函数的变换

平移变换

①\(y=f(x) \rightarrow y=f(x \pm a)(a>0)\)将\(y=f(x)\)图像沿\(x\)轴向左(右)平移\(a\)个单位(左加右减)；
②\(y=f(x) \rightarrow y=f(x) \pm b(b>0)\)将\(y=f(x)\)图像沿\(x\)轴向上(下)平移\(b\)个单位(上加下减).
注 \(f(x)=3 \sin \left(2 x+\dfrac{\pi}{3}\right)\)向左平移\(\dfrac{\pi}{4}\)个单位，得到的函数不是\(f(x)=3 \sin \left(2 x+\dfrac{\pi}{4}+\dfrac{\pi}{3}\right)\)， 而是\(f(x)=3 \sin \left[2\left(x+\dfrac{\pi}{4}\right)+\dfrac{\pi}{3}\right]\).
 

伸缩变换

① \(y=f(x)⟶ y=A f(x)(A>0)\)
将\(y=f(x)\)图像横坐标不变，纵坐标伸长到原来的\(A\)倍(\(A>1\)伸长，\(A<1\)缩短).
② \(y=f(x)⟶ y=f(ω x)(ω>0)\)
将\(y=f(x)\)图像纵坐标不变，横坐标缩到原来的\(\dfrac{1}{\omega}\)倍(\(ω>1\)缩短，\(ω<1\)伸长)；

问：怎么理解呢？
例 若将\(f(x)=3 \sin \left(x+\dfrac{\pi}{3}\right)\)图像纵坐标不变，横坐标缩到原来的\(\dfrac{1}{2}\)倍，那得到的函数是\(f(x)=3 \sin \left(2 x+\dfrac{\pi}{3}\right)\)还是\(f(x)=3 \sin \left(\dfrac{1}{2} x+\dfrac{\pi}{3}\right)\)呢？
解析 我们把\(f(x)=3 \sin \left(x+\dfrac{\pi}{3}\right)\)的图象想象成一条弹簧，若纵坐标不变，横坐标缩到原来的\(\dfrac{1}{2}\)倍，那说明弹簧被压缩了，则周期\(T\)变小，\(ω\)会变大(\(T=\dfrac{2 \pi}{\omega}\)，\(T\)与\(ω\)成反比)，即变换后的函数应该是\(f(x)=3 \sin \left(2 x+\dfrac{\pi}{3}\right)\).
 

经典例题

【题型一】函数图象的变换

【典题1】 将函数\(f(x)=A \sin \left(\omega x+\dfrac{\pi}{6}\right)\)\((A>0, \omega>0)\)的图象上的点的横坐标缩短为原来的\(\dfrac{1}{2}\)倍，再向右平移\(\dfrac{\pi}{3}\)个单位得到函数\(g(x)=2 \cos (2 x+\varphi)\)的图象，则下列说法正确的是(　　)
A．函数\(f(x)\)的最小正周期为\(π\)
B．函数\(f(x)\)的单调递增区间为\(\left[2 k \pi-\dfrac{2 \pi}{3}, 2 k \pi+\dfrac{\pi}{3}\right](k \in Z)\)
C．函数\(f(x)\)的图象有一条对称轴为\(x=\dfrac{2 \pi}{3}\)
D．函数\(f(x)\)的图象有一个对称中心为\(\left(\dfrac{2 \pi}{3}, 0\right)\)
【解析】函数\(f(x)=A \sin \left(\omega x+\dfrac{\pi}{6}\right)\)\((A>0, \omega>0)\)的图象上的点的横坐标缩短为原来的\(\dfrac{1}{2}\)倍，再向右平移\(\dfrac{\pi}{3}\)个单位得到\(f(x)=A \sin \left[2 \omega\left(x-\dfrac{\pi}{3}\right)+\dfrac{\pi}{6}\right]\)\(=A \sin \left(2 \omega x+\dfrac{\pi}{6}-\dfrac{2 \pi \omega}{3}\right)\)的图象．
与\(g(x)=2 \cos (2 x+\varphi)=2 \sin \left(2 x+\varphi+\dfrac{\pi}{2}\right)\)比较
\({\color{Red}{(利用诱导公式转化同函数名) }}\)
又由于\(A>0\)，\(ω>0\)，所以\(A=2\)，\(ω=1\)．
所以\(f(x)=2 \sin \left(x+\dfrac{\pi}{6}\right)\)
故函数\(f(x)\)的周期为\(2π\)，\(A\)错误；
令\(2 k \pi-\dfrac{\pi}{2} \leq x+\dfrac{\pi}{6} \leq 2 k \pi+\dfrac{\pi}{2}, k \in Z\)，
解得\(2 k \pi-\dfrac{2 \pi}{3} \leq x \leq 2 k \pi+\dfrac{\pi}{3}, k \in Z\)，
所以函数\(f(x)\)单调递增区间为\(\left[2 k \pi-\dfrac{2 \pi}{3}, 2 k \pi+\dfrac{\pi}{3}\right](k \in Z)\)，故\(B\)正确；
由于\(f\left(\dfrac{2 \pi}{3}\right)=2 \sin \dfrac{5 \pi}{6}=1\)，
则\(f\left(\dfrac{2 \pi}{3}\right)\)取不到最值，
\(\therefore x=\dfrac{2 \pi}{3}\)不是对称轴，
\(\because f\left(\dfrac{2 \pi}{3}\right) \neq 0\)，\(\therefore\left(\dfrac{2 \pi}{3}, 0\right)\)不是对称中心，即\(C\)，\(D\)错误．
故选：\(B\)．
 

巩固练习

1(★)将函数\(y=\cos x\)的图象先左移\(\dfrac{\pi}{4}\)，再纵坐标不变，横坐标缩为原来的\(\dfrac{1}{2}\)，所得图象的解析式为(　　)
A．\(y=\sin \left(2 x+\dfrac{\pi}{4}\right)\) \(\qquad \qquad \qquad \qquad\)B．\(y=\sin \left(\dfrac{1}{2} x+\dfrac{3 \pi}{4}\right)\)
C．\(y=\sin \left(\dfrac{1}{2} x+\dfrac{\pi}{4}\right)\) \(\qquad \qquad \qquad \qquad\)D．\(y=\sin \left(2 x+\dfrac{3 \pi}{4}\right)\)
 

2(★)将函数\(f(x)=3 \sin \left(\dfrac{1}{2} x-\varphi\right)\)\(\left(|\varphi|<\dfrac{\pi}{2}\right)\)的图象向左平移\(\dfrac{\pi}{3}\)个单位长度得到函数\(g(x)\)的图象．若\(g\left(\dfrac{\pi}{3}\right)=\dfrac{3}{2}\)，则\(φ=\)(　　)
A．\(-\dfrac{\pi}{4}\) \(\qquad \qquad \qquad \qquad\)B．\(-\dfrac{\pi}{3}\) \(\qquad \qquad \qquad \qquad\) C．\(\dfrac{\pi}{6}\) \(\qquad \qquad \qquad \qquad\) D．\(\dfrac{\pi}{3}\)
 

3(★★)为了得到函数\(f(x)=\sin \left(2 x+\dfrac{3 \pi}{4}\right)\)的图象，可以将函数\(g(x)=\cos2x\)的图象(　　)
A．向右平移\(\dfrac{\pi}{4}\)个单位\(\qquad \qquad\) B．向左平移\(\dfrac{\pi}{4}\)个单位\(\qquad \qquad\) C．向右平移\(\dfrac{\pi}{8}\)个单位 \(\qquad \qquad\)D．向左平移\(\dfrac{\pi}{8}\)个单位
 

4(★★) 已知函数\(y=\sin (\omega x+\varphi)\)的两条相邻的对称轴的间距为\(\dfrac{\pi}{2}\)，现将\(y=\sin(ωx+φ)\)的图象向左平移\(\dfrac{\pi}{8}\)个单位后得到一个偶函数，则\(φ\)的一个可能取值为(　　)
A．\(\dfrac{3 \pi}{4}\) \(\qquad \qquad \qquad \qquad\)B．\(\dfrac{\pi}{4}\) \(\qquad \qquad \qquad \qquad\)C．\(0\)\(\qquad \qquad \qquad \qquad\) D．\(-\dfrac{\pi}{4}\)
 

5(★★)已知函数\(f(x)=\sin (\omega x+\varphi)\)\(\left(\omega>0,|\varphi|<\dfrac{\pi}{2}\right)\)的最小正周期为\(π\)，且图象向右平移\(\dfrac{\pi}{12}\)个单位后得到的函数为偶函数，则\(f(x)\)的图象(　　)
A．关于点\(\left(\dfrac{5 \pi}{12}, 0\right)\)对称 \(\qquad \qquad \qquad \qquad\)B．关于直线\(x=\dfrac{\pi}{6}\)对称
C．在\(\left[-\dfrac{\pi}{12}, \dfrac{5 \pi}{12}\right]\)单调递增 \(\qquad \qquad \qquad \qquad\)D．在\(\left[\dfrac{\pi}{12}, \dfrac{7 \pi}{12}\right]\)单调递减
 

6(★★★) 将函数\(f(x)=A \sin \left(\omega x+\dfrac{\pi}{6}\right)\)\((A>0, \omega>0)\)的图象上的点的横坐标缩短为原来的\(\dfrac{1}{2}\)倍，再向右平移\(\dfrac{\pi}{3}\)个单位得到函数\(g(x)=2\cos(2x+φ)\)的图象，则下列说法正确的是(　　)
A．函数\(f(x)\)的最小正周期为\(π\)
B．函数\(f(x)\)的单调递增区间为\(\left[2 k \pi-\dfrac{2 \pi}{3}, 2 k \pi+\dfrac{\pi}{3}\right](k \in Z)\)
C．函数\(f(x)\)的图象有一条对称轴为\(x=\dfrac{2 \pi}{3}\)
D．函数\(f(x)\)的图象有一个对称中心为\(\left(\dfrac{2 \pi}{3}, 0\right)\)
 

答案

1. \(D\)
2. \(C\)
3. \(D\)
4. \(B\)
5. \(C\)
6. \(B\)

【题型二】由函数\(y=Asin(ωx+φ)\)的部分图象求解析式

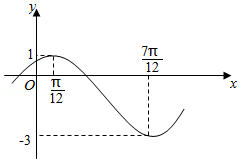
【典题1】 已知函数\(f(x)=A \sin (\omega x+\varphi)\)\(\left(A>0, \omega>0,0<|\varphi|<\dfrac{\pi}{2}\right)\)的部分图象如图所示，下述四个结论：①\(ω=2\)；②\(\varphi=-\dfrac{\pi}{3}\)；③\(f\left(x+\dfrac{\pi}{12}\right)\)是奇函数；④\(f\left(x-\dfrac{\pi}{12}\right)\)是偶函数中，其中所有正确结论的编号是 \(\underline{\quad \quad}\) .

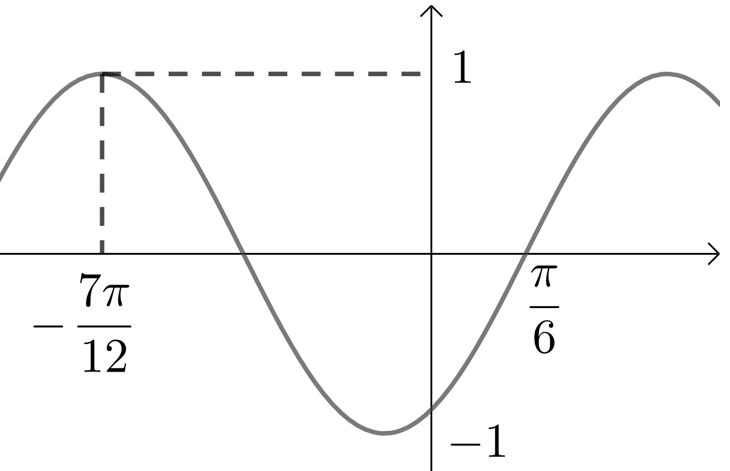
【解析】由函数图象的最值可得\(A=1\)，
由\(\dfrac{3}{4} T=\dfrac{\pi}{6}-\left(-\dfrac{7 \pi}{12}\right)=\dfrac{3 \pi}{4}\)，
解得\(T=π\)，所以\(\omega=\dfrac{2 \pi}{T}=2\)，
此时\(f(x)=\sin (2 x+\varphi)\)
代入\(\left(-\dfrac{7 \pi}{12}, 1\right)\)得\(f\left(-\dfrac{7 \pi}{12}\right)=\sin \left(-\dfrac{7 \pi}{6}+\varphi\right)=1\)，
\(\therefore-\dfrac{7 \pi}{6}+\varphi=\dfrac{\pi}{2}+2 k \pi \Rightarrow \varphi=\dfrac{5 \pi}{3}+2 k \pi,\)，
又\(\because 0<|\varphi|<\dfrac{\pi}{2}\)，\(\therefore \varphi=-\dfrac{\pi}{3}\)，
\(\therefore f(x)=\sin \left(2 x-\dfrac{\pi}{3}\right)\)，
\(∴\)①、②正确；
\(\because f\left(x+\dfrac{\pi}{12}\right)=\sin \left[2\left(x+\dfrac{\pi}{12}\right)-\dfrac{\pi}{3}\right]=\sin \left(2 x-\dfrac{\pi}{6}\right)\)不是奇函数，\(∴\)③错误；
\(\because f\left(x-\dfrac{\pi}{12}\right)=\sin \left[2\left(x-\dfrac{\pi}{12}\right)-\dfrac{\pi}{3}\right]\)\(=\sin \left(2 x-\dfrac{\pi}{2}\right)=-\cos 2 x\)，
\(\therefore f\left(x-\dfrac{\pi}{12}\right)\)为偶函数，④正确．
综上知，正确的命题序号是①②④．
【点拨】由函数\(y=A \sin (\omega x+\varphi)+B\)\((A>0, \omega>0)\)的部分图象求解析式的方法
(1) 求\(A,B\)：通过函数最值求解，由\(\left\{\begin{array}{c} f_{\max }=A+B \\ f_{\min }=-A+B \end{array}\right.\)得\(A=\dfrac{f_{\max }-f_{\min }}{2}\)，\(B=\dfrac{f_{\max }+f_{\min }}{2}\)；
(2) 求\(ω\)：根据图象求出周期\(T\)，再利用\(T=\dfrac{2 \pi}{\omega}\)求出\(ω\)；
(3) 求\(φ\)：求出\(A,ω\)后代入函数图象一最值点，求出\(φ\).
 

【典题2】 已知函数\(f(x)=\sin (\omega x+\varphi)\)\((\omega>0,0<\varphi<\pi)\)，\(f(0)=f\left(\dfrac{2}{9} \pi\right)=-f\left(\dfrac{\pi}{3}\right)\)，且\(f(x)\)在\(\left(\dfrac{\pi}{6}, \dfrac{4 \pi}{9}\right)\)上单调，则函数\(y=f(x)\)的解析式是 \(\underline{\quad \quad}\) .
【解析】 对于函数\(f(x)=\sin (\omega x+\varphi)\)，
由\(f(0)=f\left(\dfrac{2 \pi}{9}\right)\)，可得函数的图象关于直线\(x=\dfrac{1}{2}\left(0+\dfrac{2 \pi}{9}\right)=\dfrac{\pi}{9}\)对称；
又\(f\left(\dfrac{2 \pi}{9}\right)=-f\left(\dfrac{\pi}{3}\right)\)，
可得函数图象关于点\(\left(\dfrac{\frac{2 \pi}{9}+\frac{\pi}{3}}{2}, 0\right)\)对称，即\(\left(\dfrac{5 \pi}{18}, 0\right)\)；
\(\therefore \dfrac{T}{4}+k T=\dfrac{5 \pi}{18}-\dfrac{\pi}{9}=\dfrac{\pi}{6}\)，\(k∈Z\),
解得\(T=\dfrac{2 \pi}{3(4 k+1)}\)；
\(\therefore \omega=\dfrac{2 \pi}{T}=3(4 k+1)\)
\(\because f(x)\)在\(\left(\dfrac{\pi}{6}, \dfrac{4 \pi}{9}\right)\)上单调
\(\therefore \dfrac{T}{2} \geq \dfrac{4 \pi}{9}-\dfrac{\pi}{6}\)，解得\(T>\dfrac{5 \pi}{9}\)
\({\color{Red}{(由单调区间得到周期范围)}}\)
\(\therefore 0<\omega \leq \dfrac{18}{5}\)
又\(\omega=\dfrac{2 \pi}{T}=3(4 k+1)\)，\(\therefore \omega=3\)
\(\because\left(\dfrac{5 \pi}{18}, 0\right)\)是对称中心，\(\therefore f\left(\dfrac{5 \pi}{18}\right)=0\)
即\(\sin \left(3 \times \dfrac{5 \pi}{18}+\varphi\right)=0\)，又\(\because 0<\varphi<\pi\)，\(\therefore \varphi=\dfrac{\pi}{6}\)
\(\therefore f(x)=\sin \left(3 x+\dfrac{\pi}{6}\right)\)
【点拨】
①对于函数\(y=A \sin (\omega x+\varphi)\)，
若\(f(a)=f(b)\)，则\(x=\dfrac{a+b}{2}\)是其对称轴；
若\(f(a)=-f(b)\)，则\(\left(\dfrac{a+b}{2}, 0\right)\)是其对称中心；
②处理三角函数\(f(x)=A \sin (\omega x+\varphi)\)，多注意其对称性，结合图象进行分析.
 

巩固练习

1(★)函数\(f(x)=A\sin( ωx+φ)\)(其中\(A>0\)，\(ω>0\)，\(|\varphi|<\dfrac{\pi}{2}\))的图象如图，则此函数表达式为 \(\underline{\quad \quad}\) .

 
 

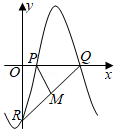
2(★★) 如图，函数\(y=A \sin (\omega x+\varphi)\)\(\left(A>0, \omega>0,|\varphi| \leq \dfrac{\pi}{2}\right)\)与坐标轴的三个交点\(P、Q、R\)满足\(P(1,0)\)，\(\angle P Q R=\dfrac{\pi}{4}\)，\(M\)为\(QR\)的中点，\(P M=\dfrac{\sqrt{34}}{2}\)，则\(A\)的值为 \(\underline{\quad \quad}\) .

 

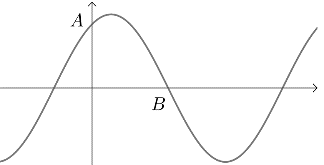
3(★★)已知函数\(f(x)=2 \sin (\omega x+\varphi)\)\((\omega>0,0<\varphi<\pi)\)的部分图象如图所示，点\(A(0, \sqrt{3})\)，\(B\left(\dfrac{\pi}{3}, 0\right)\)，则下列说法中错误的是(　　)

A．直线\(x=\dfrac{\pi}{12}\)是\(f(x)\)图象的一条对称轴
B．\(f(x)\)的图象可由\(g(x)=2 \sin 2 x\)向左平移\(\dfrac{\pi}{3}\)个单位而得到
C．\(f(x)\)的最小正周期为π
D．\(f(x)\)在区间\(\left(-\dfrac{\pi}{3}, \dfrac{\pi}{12}\right)\)上单调递增
 

4 (★★★)已知函数\(f(x)=A \sin (\omega x+\varphi)+B\)\(\left(A>0, \omega>0,|\varphi|<\dfrac{\pi}{2}\right)\)的部分图象如图所示．
(1)求\(f(x)\)的解析式；
(2)求\(f(x)\)的单调递增区间和对称中心坐标；
(3)将\(f(x)\)的图象向左平移$\dfrac{\pi}{6} $个单位，再讲横坐标伸长到原来的\(2\)倍，纵坐标不变，最后将图象向上平移\(1\)个单位，得到函数\(g(x)\)的图象，求函数\(y=g(x)\)在\(x \in\left[0, \dfrac{7 \pi}{6}\right]\)上的最大值和最小值．

 
 

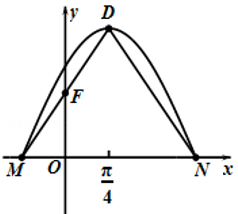
5 (★★★)如图是函数\(f(x)=A \sin (\omega x+\varphi)\)\(\left(A>0, \omega>0,0<\varphi<\dfrac{\pi}{2}\right)\)的部分图象，\(M、N\)是它与\(x\)轴的两个不同交点，\(D\)是\(M、N\)之间的最高点且横坐标为\(\dfrac{\pi}{4}\)，点\(F(0,1)\)是线段\(DM\)的中点．
(1)求函数\(f(x)\)的解析式及\([π,2π]\)上的单调增区间；
(2)若\(x \in\left[-\dfrac{\pi}{12}, \dfrac{5 \pi}{12}\right]\)时，函数\(h(x)=f^2 (x)-\)\(af(x)+1\)的最小值为\(\dfrac{1}{2}\),求实数\(a\)的值．

 
 

参考答案

1. \(f(x)=3 \sin \left(\dfrac{1}{2} x+\dfrac{\pi}{4}\right)\)
2. \(5 \sqrt{2}\)
3. \(B\)
4. \((1) f(x)=2 \sin \left(2 x+\dfrac{\pi}{3}\right)-1\)
   \((2)\)单调递增区间\(\left[k \pi-\dfrac{5 \pi}{12}, k \pi+\dfrac{\pi}{12}\right], k \in Z\)，对称中心坐标\(\left(\dfrac{k \pi}{2}-\dfrac{\pi}{6},-1\right), k \in Z\)
   \((3)\)最小值\(-2\),最大值\(\sqrt{3}\).
5. \(\text { (1) } f(x)=2 \sin \left(x+\dfrac{\pi}{4}\right),\left[\dfrac{5 \pi}{4}, 2 \pi\right]\)，
   \(\text { (2) } \dfrac{3}{2}\)
    

【题型三】三角函数模型的简单应用一

【典题1】已知函数\(f(x)=\sin ^{2} x-2 \sqrt{3} \sin x \cos x+\sin \left(x+\dfrac{\pi}{4}\right) \sin \left(x-\dfrac{\pi}{4}\right)\)．
(1)求\(f(x)\)的最小值并写出此时\(x\)的取值集合；
(2)若\(x∈[0 ,π]\)，求出\(f(x)\)的单调减区间.

【解析】(1)由于\(f(x)=\sin ^{2} x-2 \sqrt{3} \sin x \cos x+\sin \left(x+\dfrac{\pi}{4}\right) \sin \left(x-\dfrac{\pi}{4}\right)\)
\(=\dfrac{1-\cos 2 x}{2}-\sqrt{3} \sin 2 x+\dfrac{\sqrt{2}}{2}(\sin x+\cos x) \dfrac{\sqrt{2}}{2}(\sin x-\cos x)\)
\({\color{Red} {（二倍角公式、两角和差公式）}}\)
\(=\dfrac{1-\cos 2 x}{2}-\sqrt{3} \sin 2 x-\dfrac{\cos 2 x}{2}\)
\(=\dfrac{1}{2}-(\sqrt{3} \sin 2 x+\cos 2 x)\)
\({\color{Red} {(辅助角公式)}}\)
\(=\dfrac{1}{2}-2 \sin \left(2 x+\dfrac{\pi}{6}\right)\)
令\(2 x+\dfrac{\pi}{6}=2 k \pi+\dfrac{\pi}{2}\)，\(k∈Z\)，解得\(x=k \pi+\dfrac{\pi}{6}\)，\(k∈Z\)，
可得\(f(x)\)的最小值为\(-\dfrac{3}{2}\)，
此时\(x\)的取值集合为\(\left\{x \mid x=\dfrac{\pi}{6}+k \pi, k \in Z\right\}\)；
(2)由\(2 k \pi-\dfrac{\pi}{2} \leq 2 x+\dfrac{\pi}{6} \leq 2 k \pi+\dfrac{\pi}{2}\)，\(k∈Z\)，
可得\(k \pi-\dfrac{\pi}{3} \leq x \leq k \pi+\dfrac{\pi}{6}\)，\(k∈Z\)，
所以\(f(x)\)的单调减区间为\(\left[k \pi-\dfrac{\pi}{3}, k \pi+\dfrac{\pi}{6}\right]\)，\(k∈Z\)，
因为\(x∈[0 ,π]\)，当\(k=0\)时，减区间为\(\left[0, \dfrac{\pi}{6}\right]\)；
当\(k=1\)时，减区间为\(\left[\dfrac{2 \pi}{3}, \pi\right]\)．
综上，\(x∈[0 ,π]\)时的单调减区间为\(\left[0, \dfrac{\pi}{6}\right]\)和\(\left[\dfrac{2 \pi}{3}, \pi\right]\)．
【点拨】
① 解析式的化简中用积化和差公式\(\sin \left(x+\dfrac{\pi}{4}\right) \sin \left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\left[\cos \dfrac{\pi}{2}-\cos 2 x\right]=-\dfrac{1}{2} \cos 2 x\)更简洁些；
②本题通过各种公式(两角和差公式、倍角公式、积化和差公式等)转化，最终把函数的解析式转化为\(f(x)=A \sin (\omega x+\varphi)+B\)或\(f(x)=A\cos(ωx+φ)+B\)的形式求解函数的各性质(单调性、对称性、周期、最值等).
 

【典题2】已知函数\(f(x)=4 \sin ^{2}\left(\dfrac{\pi}{4}+\dfrac{x}{2}\right) \sin x+(\cos x+\sin x)(\cos x-\sin x)-1\)．
(1)求\(f(x)\)的对称中心；
(2)设常数\(ω>0\)，若函数\(y=f(ωx)\)在区间\(\left[-\dfrac{\pi}{2}, \dfrac{2 \pi}{3}\right]\)上是增函数，求\(ω\)的取值范围；
(3)若函数\(g(x)=\dfrac{1}{2}\left[f(2 x)+a f(x)-a f\left(\dfrac{\pi}{2}-x\right)-a\right]-1\)在区间\(\left[-\dfrac{\pi}{4}, \dfrac{\pi}{2}\right]\)上的最大值为\(2\)，求\(a\)的值．
【解析】(1) \({\color{Red} {(函数解析式转化为f(x)=Asin(ωx+φ)+B形式)}}\)
\(f(x)=2\left[1-\cos \left(\dfrac{\pi}{2}+x\right)\right] \cdot \sin x+\cos ^{2} x-\sin ^{2} x-1\)
\(=\sin x(2+2 \sin x)+1-2 \sin ^{2} x-1=2 \sin x\)．
所以对称中心\((kπ ,0)\)，\(k∈Z\)，
(2)\(∵f(ωx)=2\sinωx\)，由\(-\dfrac{\pi}{2}+2 k \pi \leq \omega x \leq \dfrac{\pi}{2}+2 k \pi\)，
解得\(-\dfrac{\pi}{2 \omega}+\dfrac{2 k \pi}{\omega} \leq x \leq \dfrac{\pi}{2 \omega}+\dfrac{2 k \pi}{\omega}\)，
\(∴f(ωx)\)的增区间为\(\left[-\dfrac{\pi}{2 \omega}+\dfrac{2 k \pi}{\omega}, \dfrac{\pi}{2 \omega}+\dfrac{2 k \pi}{\omega}\right]\) ,\(k∈Z\)，
\(∵f(ωx)\)在\(\left[-\dfrac{\pi}{2}, \dfrac{2 \pi}{3}\right]\)上是增函数，
\({\color{Red} {(\left[-\dfrac{\pi}{2}, \dfrac{2 \pi}{3}\right]是函数f(ωx)增区间的子集，而0 \in\left[-\dfrac{\pi}{2}, \dfrac{2 \pi}{3}\right]，故k=0)}}\)
\(∴\)当\(k=0\)时，有\(\left[-\dfrac{\pi}{2}, \dfrac{2 \pi}{3}\right] \subseteq\left[-\dfrac{\pi}{2 \omega}, \dfrac{\pi}{2 \omega}\right]\)，
\(\therefore\left\{\begin{array}{l} \omega>0 \\ -\dfrac{\pi}{2 \omega} \leq-\dfrac{\pi}{2} \\ \dfrac{\pi}{2 \omega} \geq \dfrac{2 \pi}{3} \end{array}\right.\)，解得\(0<\omega \leq \dfrac{3}{4}\)，
\(∴ω\)的取值范围是\(\left(0, \dfrac{3}{4}\right]\)．
(3)\(g(x)=2 \sin x \cos x+a(\sin x-\cos x)-\dfrac{1}{2} a-1\)，
\({\color{Red} {(注意(\sin x-\cos x)^{2}=1-\sin 2 x,(\sin x+\cos x)^{2}=1+\sin 2 x)}}\)
令\(\sin x-\cos x=t\)，
则\(t=\sin x-\cos x=\sqrt{2} \sin \left(x-\dfrac{\pi}{4}\right)\)，
\(\because x \in\left[-\dfrac{\pi}{4}, \dfrac{\pi}{2}\right]\)，\(\therefore x-\dfrac{\pi}{4} \in\left[-\dfrac{\pi}{2}, \dfrac{\pi}{4}\right]\)，\(\therefore-\sqrt{2} \leq t \leq 1\)
而\(\sin2x=1-t^2\)，
则\(y=1-t^{2}+a t-\dfrac{1}{2} a-1=-\left(t-\dfrac{a}{2}\right)^{2}+\dfrac{a^{2}}{4}-\dfrac{1}{2} a\)，
\({\color{Red} {(问题转化为动轴定区间最值问题，分对称轴t=\dfrac{a}{2}在区间[-\sqrt{2}, 1]左中右)}}\)
①当\(\dfrac{a}{2}<-\sqrt{2}\)时，即\(a<-2 \sqrt{2}\)时，\(y_{\max }=-\left(-\sqrt{2}-\dfrac{a}{2}\right)^{2}+\dfrac{a^{2}}{4}-\dfrac{a}{2}=-\sqrt{2} a-\dfrac{a}{2}-2\)，
令\(-\sqrt{2} a-\dfrac{a}{2}-2=2\)，解得\(a=-\dfrac{8}{2 \sqrt{2}+1}\)(舍)．
②当\(-\sqrt{2} \leq \dfrac{a}{2} \leq 1\)时，即\(-2 \sqrt{2} \leq a \leq 2\)时，\(y_{\max }=\dfrac{a^{2}}{4}-\dfrac{a}{2}\)，
令\(\dfrac{a^{2}}{4}-\dfrac{a}{2}=2\)，解得\(a=-2\)或\(a=4\)(舍)，
③当\(\dfrac{a}{2}>1\)时，即\(a>2\)时，在\(t=1\)处，\(y_{\max }=\dfrac{a}{2}-1\)，
由\(\dfrac{a}{2}-1=2\)，解得\(a=6\)，
综上所述\(a=－2\)或\(6\)．
 

【典题3】已知函数\(f(x)=\sin ^{4} x+\cos ^{4} x+a\sin x \cos x(a \in R)\)．
(1)当\(a=0\)时，求函数\(y=f(x)\)的单调减区间；
(2)设方程\(f(x)-a\sin2x-1=0\)在\(\left(0, \dfrac{\pi}{2}\right)\)内有两个相异的实数根\(x_1、x_2\)，求实数\(a\)的取值范围及\(x_1+x_2\)的值；
(3)若对任意实数\(x\)，\(f(x)≥0\)恒成立，求实数\(a\)的取值范围．
【解析】(1) \(f(x)=\sin ^{4} x+\cos ^{4} x+a \sin x \cos x\)　
\(=\left(\sin ^{2} x+\cos ^{2} x\right)^{2}-2 \sin ^{2} x \cos ^{2} x+a \sin x \cos x\)
\(=1-\dfrac{1}{2} \sin ^{2} 2 x+\dfrac{1}{2} a \sin 2 x\)．
当\(a=0\)时，\(f(x)=1-\dfrac{1}{2} \sin ^{2} 2 x=1-\dfrac{1-\cos 4 x}{4}=\dfrac{1}{4} \cos 4 x+\dfrac{3}{4}\)，
\({\color{Red} {(函数化为f(x)=Acos(ωx+φ)+B)}}\)
由\(2kπ≤4x≤π+2kπ\)，得\(\dfrac{k \pi}{2} \leq x \leq \dfrac{\pi}{4}+\dfrac{k \pi}{2}\)，\(k∈Z\)．
\(∴\)当\(a=0\)时，函数\(y=f(x)\)的单调减区间为\(\left[\dfrac{k \pi}{2}, \dfrac{k \pi}{2}+\dfrac{\pi}{4}\right]\)，\(k∈Z\)；
(2) \({\color{Red} {(将问题逐步等价转化，化成“最简问题”)}}\)
方程\(f(x)-a\sin2x-1=0\)在\(\left(0, \dfrac{\pi}{2}\right)\)内有两个相异的实数根\(x_1、x_2\)，
即\(1-\dfrac{1}{2} \sin ^{2} 2 x+\dfrac{1}{2} a \sin 2 x-a \sin 2 x-1=0\)在\(\left(0, \dfrac{\pi}{2}\right)\)内有两个相异的实数根\(x_1 、x_2\)，
也就是\(\sin ^{2} 2 x+a \sin 2 x=0\)在\(\left(0, \dfrac{\pi}{2}\right)\)内有两个相异的实数根\(x_1 、x_2\)，
当\(x \in\left(0, \dfrac{\pi}{2}\right)\)时，\(\sin2x≠0\)，
即\(a=-\sin2x\)在\(\left(0, \dfrac{\pi}{2}\right)\)内有两个相异的实数根\(x_1 、x_2\)，
\({\color{Red} {(数形结合，y=a与y=-\sin2x在\left(0, \dfrac{\pi}{2}\right)内相交于两点)}}\)
易得\(y=-\sin2x\)在\(\left(0, \dfrac{\pi}{2}\right)\)内的值域是\((-1,0)\)，
即\(－1<a<0\)，此时\(x_{1}+x_{2}=\dfrac{\pi}{2}\)；
(3)若对任意实数\(x\)，\(f(x)≥0\)恒成立，
则\(1-\dfrac{1}{2} \sin ^{2} 2 x+\dfrac{1}{2} \operatorname{asin} 2 x \geq 0\)恒成立，
即\(\sin^2 2x-a\sin2x-2≤0\)恒成立，
\({\color{Red} {(换元法化为二次函数恒成立问题)}}\)
令\(t=\sin2x(-1≤t≤1)\)，则\(t^2-at-2≤0\)恒成立．
可得\(\left\{\begin{array}{l} (-1)^{2}+a-2 \leq 0 \\ 1^{2}-a-2 \leq 0 \end{array}\right.\)，即\(-1≤a≤1\)．
\(∴\)实数\(a\)的取值范围是\([-1 ,1]\)．
 

巩固练习

1(★★)已知函数\(f(x)=\sqrt{3} \sin x \cos x-\sin ^{2} x\)．
(1)求函数\(f(x)\)的最小正周期；
(2)求函数\(f(x)\)的单调增区间；
(3)求函数\(f(x)\)在区间\(\left[0, \dfrac{\pi}{2}\right]\)上的最大值．
 
 

2(★★)已知函数\(f(x)=\sin (\pi-\omega x) \cos \omega x-\cos ^{2}\left(\omega x+\dfrac{\pi}{4}\right)(\omega>0)\)的最小正周期为\(π\)．
(1)求\(f(x)\)图象的对称轴方程；
(2)将\(f(x)\)图象向右平移\(\dfrac{\pi}{6}\)个单位长度后，得到函数\(g(x)\)，求函数\(g(x)\)在\(\left[0, \dfrac{\pi}{2}\right]\)上的值域．
 
 

3(★★★) 已知函数\(f(x)=\dfrac{1}{2} \cos 2 x+\sin x \cos x\)，其中\(x∈R\)．
(1)求使\(f(x) \geq \dfrac{1}{2}\)的\(x\)的取值范围；
(2)若函数\(g(x)=\dfrac{\sqrt{2}}{2} \sin \left(2 x+\dfrac{3 \pi}{4}\right)\)，且对任意的\(0≤x_1<x_2≤t\)，恒有\(f(x_1 )－f(x_2 )<g(x_1 )-g(x_2)\)成立，求实数\(t\)的最大值．
 
 

4(★★★★)已知函数\(f(x)=\sqrt{3} \sin (2 \omega x+\varphi)+1\)\(\left(\omega>0,-\dfrac{\pi}{2}<\varphi<\dfrac{\pi}{2}\right)\)，函数\(f(x)\)的图象经过点\(\left(-\dfrac{\pi}{12}, 1\right)\)且\(f(x)\)的最小正周期为\(\dfrac{\pi}{2}\)．
(1)求函数\(f(x)\)的解析式；
(2)将函数\(y=f(x)\)图象上所有的点向下平移\(1\)个单位长度，再函数图象上所有点的横坐标变为原来的\(2\)倍，纵坐标不变，再将图象上所有的点的横坐标不变，纵坐标变为原来的\(\dfrac{2 \sqrt{3}}{3}\)倍，得到函数\(y=h(x)\)图象，令函数\(g(x)=h(x)+1\)，区间\([a ,b]\)(\(a ,b∈R\)且\(a<b\))满足：\(y=g(x)\)在\([a ,b]\)上至少有\(30\)个零点，在所有满足上述条件的\([a ,b]\)中，求\(b-a\)的最小值．
(3)若\(m\left[1+\sqrt{3}\left(f\left(\dfrac{x}{8}-\dfrac{\pi}{12}\right)-1\right)\right]+\dfrac{1}{2}+\dfrac{3}{2} \cos x \leq 0\)对任意\(x∈[0 ,2π]\)恒成立，求实数\(m\)的取值范围．
 
 
 
 

参考答案

1. \((1) π\) \(\text { (2) }\left[-\dfrac{\pi}{3}+k \pi, \dfrac{\pi}{6}+k \pi\right], \quad(k \in Z)\) \(\text { (3) } \dfrac{1}{2}\)

2. \(\text { (1) } x=\dfrac{k \pi}{2}+\dfrac{\pi}{4}(k \in Z)\) \(\text { (2) }\left[-\dfrac{\sqrt{3}}{2}-\dfrac{1}{2}, \dfrac{1}{2}\right]\)．

3. \(\text { (1) }\left[k \pi, k \pi+\dfrac{\pi}{4}\right], \quad k \in Z\) \(\text { (2) } \dfrac{\pi}{4}\)

4. \(\text { (1) } f(x)=\sqrt{3} \sin \left(4 x+\dfrac{\pi}{3}\right)+1\)

   \(\text { (2) } \dfrac{43 \pi}{3}\) \(\text { (3) }(-\infty,-2]\)

 

【题型四】三角函数模型的简单应用二

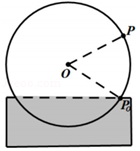
【典题1】 如图，一个水轮的半径为\(6m\)，水轮轴心\(O\)距离水面的高度为\(3m\)，已知水轮按逆时针匀速转动，每分钟转动\(5\)圈，当水轮上点\(P\)从水中浮现时的起始(图中点\(P_0\))开始计时，记\(f(t)\)为点\(P\)距离水面的高度关于时间\(t(s)\)的函数，则下列结论正确的是(　　)
A．\(f(3)=9\)
B．\(f(1)=f(7)\)
C．若\(f(t)≥6\)，则\(t \in[2+12 k, 5+12 k](k \in N)\)
D．不论\(t\)为何值，\(f(t)+f(t+4)+f(t+8)\)是定值

【解析】\({\color{Red}{方法一 几何法}}\)
图中\(PB⊥\)水面，\(OA⊥PB\)，

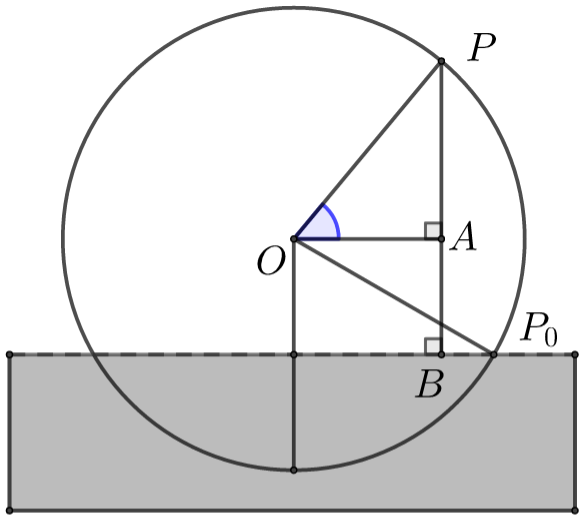
\({\color{Red}{(由图f(t)=PA=PA+3，则需了解PA与t的关系，从几何角度求解)}}\)
\(∵\)每分钟转动\(5\)圈
\(∴OP\)每秒钟内所转过的角度为\(\dfrac{5 \times 2 \pi}{60}=\dfrac{\pi}{6}\)，
\({\color{Red}{(角速度)}}\)
则\(t\)秒转过的角度\(\dfrac{\pi}{6} t\)，即\(\angle P_{0} O P=\dfrac{\pi}{6} t\)
如上图依题意可知\(\angle P_{0} O A=\dfrac{\pi}{6}\)，
即\(\alpha=\dfrac{\pi}{6} t-\dfrac{\pi}{6}\)
在\(\text { Rt } \Delta P O A\)中，\(P A=O P \sin \alpha=6 \sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)\)
\(\therefore f(t)=P B=P A+A B=6 \sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+3\)
对于\(A\)，\(f(3)=6 \sin \left(\dfrac{\pi}{6} \times 3-\dfrac{\pi}{6}\right)+3=3 \sqrt{3}+3\)，即\(A\)错误；
对于\(B\)，\(f(1)=6 \sin \left(\dfrac{\pi}{6} \times 1-\dfrac{\pi}{6}\right)+3=3\)，\(f(7)=6 \sin \left(\dfrac{\pi}{6} \times 7-\dfrac{\pi}{6}\right)+3=3\)，
即\(B\)正确；
\({\color{Red}{(或确定x=\dfrac{1+7}{2}=4是函数对称轴也行)}}\)
对于\(C\)，因为\(f(t)≥6\)，
所以\(6 \sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+3 \geq 6\)，
即\(\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right) \geq \dfrac{1}{2}\)，
所以\(\dfrac{\pi}{6} t-\dfrac{\pi}{6} \in\left[\dfrac{\pi}{6}+2 k \pi, \dfrac{5 \pi}{6}+2 k \pi\right]\)，
解得\(t∈[2+12k,6+12k],k∈N\)，
即\(C\)错误；
对于\(D\)，\(f(t)+f(t+4)+f(t+8)\)
\(=6 \sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+6 \sin \left(\dfrac{\pi}{6} t+\dfrac{\pi}{2}\right)+6 \sin \left(\dfrac{\pi}{6} t+\dfrac{7 \pi}{6}\right)+9\)
\(=6\left[\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+\cos \dfrac{\pi}{6} t-\sin \left(\dfrac{\pi}{6} t+\dfrac{\pi}{6}\right)\right]+9\)
因为\(\sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+\cos \dfrac{\pi}{6} t-\sin \left(\dfrac{\pi}{6} t+\dfrac{\pi}{6}\right)=0\)，
所以\(f(t)+f(t+4)+f(t+8)=9\)，
即\(D\)正确．
故选：\(BD\)．
\({\color{Red}{方法二 待定系数法}}\)
可知\(f(x)\)符合三角函数模型，
设\(f(t)=Asin(ωx+φ)+B(A>0)\)，
依题意可知\(f(t)\)的最大值为\(9\)，最小为\(-3\)，
\(∴A+B=9\)，且\(-A+B=-3\)，
可得\(A=6\)，\(B=3\)；
\(∵\)每分钟转动\(5\)圈，
\(∴1\)圈要\(12\)秒，即\(T=12s\)，
则\(\omega=\dfrac{2 \pi}{T}=\dfrac{\pi}{6}\)，得\(f(t)=6 \sin \left(\dfrac{\pi}{6} t+\varphi\right)+3\)，
\({\color{Red}{(也可由OP每秒钟内所转过的角度为\dfrac{5 \times 2 \pi}{60}=\dfrac{\pi}{6}得\omega=\dfrac{\pi}{6}}}\)
依题意可知\(f(0)=0\)，
得\(\sin \varphi=-\dfrac{1}{2}\)，取\(\varphi=-\dfrac{\pi}{6}\)，
\({\color{Red}{(得到φ的一个值便可)}}\)
故所求的函数解析式为\(f(t)=6 \sin \left(\dfrac{\pi}{6} t-\dfrac{\pi}{6}\right)+3\)，
接下来如同方法一.

【点拨】
① 方法一利用几何性质求出\(f(t)\)(即图中的\(PB\))与t之间的关系；
② 方法二是根据题意确定符合三角函数模型，则用待定系数法设函数\(f(t)=A\sin(ωx+φ)+B\)，根据题意由最大值和最小值求出\(A,B\)的值，根据周期性由\(T=\dfrac{2 \pi}{\omega}\)求出\(ω\)，注意一个特殊情况代入一个点求出\(φ\).
 
 

【典题2】 某公司欲生产一款迎春工艺品回馈消费者，工艺品的平面设计如图所示，该工艺品由直角\(△ABC\)和以\(BC\)为直径的半圆拼接而成，点\(P\)为半圈上一点(异于\(B,C\))，点\(H\)在线段\(AB\)上，且满足\(CH⊥AB\)．已知\(∠ACB=90°\)，\(AB=1dm\)，设\(∠ABC=θ\)．
(1)为了使工艺礼品达到最佳观赏效果，需满足\(∠ABC=∠PCB\)，且\(CA+CP\)达到最大．当\(θ\)为何值时，工艺礼品达到最佳观赏效果；
(2)为了工艺礼品达到最佳稳定性便于收藏，需满足\(∠PBA=60°\)，且\(CH+CP\)达到最大．当\(θ\)为何值时，\(CH+CP\)取得最大值，并求该最大值．

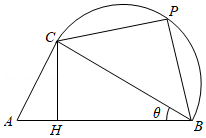
【解析】依题意\(∠ABC=∠PCB=θ\)，
则在直角\(△ABC\)中，\(AC=\sinθ,BC=\cosθ\)
在直角\(△PBC\)中，\(P C=B C \cdot \cos \theta=\cos ^{2} \theta\)，\(P B=B C \cdot \sin \theta=\sin \theta \cos \theta\)
\({\color{Red}{(用变量θ表示CA+CP，利用函数最值方法求解)}}\)
(1)\(A C+C P=\sin \theta+\cos ^{2} \theta\)\(=\sin \theta+1-\sin ^{2} \theta=-\sin ^{2} \theta+\sin \theta+1\)，\(\theta \in\left(0, \dfrac{\pi}{2}\right)\)，
所以当\(\sin \theta=\dfrac{1}{2}\)，即\(\theta=\dfrac{\pi}{6}\)，\(AC+CP\)的最大值为\(\dfrac{5}{4}\)；
(2)在直角\(△ABC\)中，由\(S_{\triangle A B C}=\dfrac{1}{2} C A \cdot C B=\dfrac{1}{2} A B \cdot C H,\)，\({\color{Red}{(等积法)}}\)
可得\(C H=\dfrac{\sin \theta \cdot \cos \theta}{1}=\sin \theta \cdot \cos \theta\)；
在直角\(△PBC\)中，
\(P C=B C \cdot \sin \left(\dfrac{\pi}{3}-\theta\right)\)\(=\cos \theta \cdot\left(\sin \dfrac{\pi}{3} \cos \theta-\cos \dfrac{\pi}{3} \sin \theta\right)\)\(=\dfrac{\sqrt{3}}{2} \cos ^{2} \theta-\dfrac{1}{2} \cos \theta \sin \theta\)，
所以\(C H+C P=\dfrac{\sqrt{3}}{2} \cos ^{2} \theta+\dfrac{1}{2} \cos \theta \sin \theta\)
\(=\dfrac{1}{4} \sin 2 \theta+\dfrac{\sqrt{3}}{4} \cos 2 \theta+\dfrac{\sqrt{3}}{4}=\dfrac{1}{2} \sin \left(2 \theta+\dfrac{\pi}{3}\right)+\dfrac{\sqrt{3}}{4}\)，\(\theta \in\left(0, \dfrac{\pi}{2}\right)\)，
\({\color{Red}{(函数化为f(x)=A \sin (\omega x+\varphi)+B求最值)}}\)
所以当\(\theta=\dfrac{\pi}{12}\)，\(CH+CP\)达到最大，最大值为\(\dfrac{1}{2}+\dfrac{\sqrt{3}}{4}\)．
【点拨】
① 利用直角三角形等几何性质用\(θ\)表示各线段长度；
② 题目中体现了函数思想，在求解实际问题中，特别要注意自变量θ的取值范围.
 
 

巩固练习

1(★★) 水车在古代是进行灌溉引水的工具，是人类的一项古老的发明，也是人类利用自然和改造自然的象征．如图是一个半径为\(R\)的水车，一个水斗从点\(A(3 \sqrt{3},-3)\)出发，沿圆周按逆时针方向匀速旋转，且旋转一周用时\(60\)秒．经过\(t\)秒后，水斗旋转到\(P\)点，设\(P\)的坐标为\((x,y)\)，其纵坐标满足\(y=f(t)=R \sin (\omega t+\varphi)\left(t \geq 0, \omega>0,|\varphi|<\dfrac{\pi}{2}\right)\)．则下列叙述错误的是(　　)

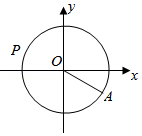
A．\(R=6, \omega=\dfrac{\pi}{30}, \varphi=-\dfrac{\pi}{6}\)
B．当\(t∈[35,55]\)时，点\(P\)到\(x\)轴的距离的最大值为\(6\)
C．当\(t∈[10,25]\)时，函数\(y=f(t)\)单调递减
D．当\(t=20\)时，\(|P A|=6 \sqrt{3}\)
 
 

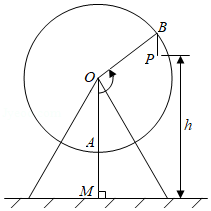
2(★★)某游乐场中半径为\(30\)米的摩天轮逆时针(固定从一侧观察)匀速旋转，每\(5\)分钟转一圈，其最低点离底面\(5\)米，如果以你从最低点登上摩天轮的时刻开始计时，那么你与底面的距离高度\(y\)(米)随时间\(t\)(秒)变化的关系式为 \(\underline{\quad \quad}\) .

 
 

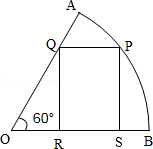
3(★★) 如图，已知扇形\(AOB\)的半径为\(1\)，中心角为\(60°\)，四边形\(PQRS\)是扇形的内接矩形，\(P\)为\(\widehat{A B}\)上一动点，问：点\(P\)在怎样的位置时，矩形\(PQRS\)的面积最大？并求出这个最大值．

 
 

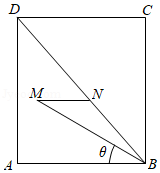
4(★★★) 如图，某正方形公园\(ABCD\)，在\(ABD\)区域内准备修建三角形花园\(BMN\)，满足\(MN\)与\(AB\)平行(点\(N\)在\(BD\)上)，且\(AB=AD=BM=2\)(单位：百米)．设\(∠ABM=θ\)，\(△BMN\)的面积为\(S\)(单位：百米平方)．
(1)求\(S\)关于\(θ\)的函数解析式
(2)求\(S(θ)\)的最大值，并求出取到最大值时\(θ\)的值．

 
 

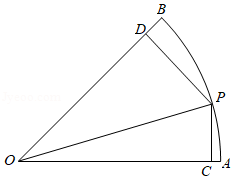
5(★★★)某农场有一块扇形农田，如图所示．已知扇形\(OAB\)的圆心角为\(\dfrac{\pi}{4}\)，半径为\(80\)米，点\(P\)在\(\widehat{A B}\)上，\(PC⊥OA\)于\(C\)，\(PD⊥OB\)于\(D\)．现要在\(△OPC\)和\(△OPD\)区域中分别种植甲、乙两种蔬菜，且甲、乙两种蔬菜单位面积年产值之比为\(\text { 1: } \sqrt{3}\)．设\(∠AOP=θ\)，\(0<\theta<\dfrac{\pi}{4}\)．
(1)用\(θ\)分别表示\(△OPC\)和\(△OPD\)的面积；
(2)当\(θ\)为何值时，读农场种植甲、乙两种蔬菜的年总产值最大？

 
 

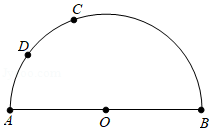
6(★★★★) 如图，半圆的直径\(AB=2\)，\(O\)为圆心，\(C\)，\(D\)为半圆上的点．
(1)请你为\(C\)点确定位置，使\(△ABC\)的周长最大，并说明理由；
(2)已知\(AD=DC\)，设\(∠ABD=θ\)，当\(θ\)为何值时，
①四边形\(ABCD\)的周长最大，最大值是多少？
②四边形\(ABCD\)的面积最大，最大值是多少？

 
 
 
 

参考答案

1. \(C\)
2. \(y=30 \sin \left(\dfrac{\pi}{150} t-\dfrac{\pi}{2}\right)+35\)
3. 当\(P\)为\(\widehat{A B}\)中点时，矩形\(PQRS\)的面积取到最大值\(\dfrac{\sqrt{3}}{6}\)
4. \(\text { (1) } S(\theta)=2 \sin \theta(\cos \theta-\sin \theta), \quad \theta \in\left(0, \dfrac{\pi}{4}\right)\)
   \((2) S(θ)\)的最大值为\(\sqrt{2}-1\)百米平方，此时\(\theta=\dfrac{\pi}{8}\)．
5. \((1) △OPC\)和\(△OPD\)的面积分别为\(1600\sin2θ\)平方米，\(1600\cos2θ\)平方米；
   \((2)\)当\(\theta=\dfrac{\pi}{12}\)时，该农场种植甲，乙两种蔬菜的年总产值量大.
6. \(\text { (1) } 2 \sqrt{2}+2\)，此时点\(C\)是半圆的中点
   \((2)\)① \(\theta=\dfrac{\pi}{6}\)时，最大值是\(5\)． ② \(\theta=\dfrac{\pi}{6}\)时，最大值是\(\dfrac{3 \sqrt{3}}{4}\).