5.4 三角函数的图像与性质
\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【高分突破系列】高一数学上学期同步知识点剖析精品讲义与分层练习]
(https://www.zxxk.com/docpack/2783085.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
必修第一册同步拔高练习,难度3颗星!
模块导图
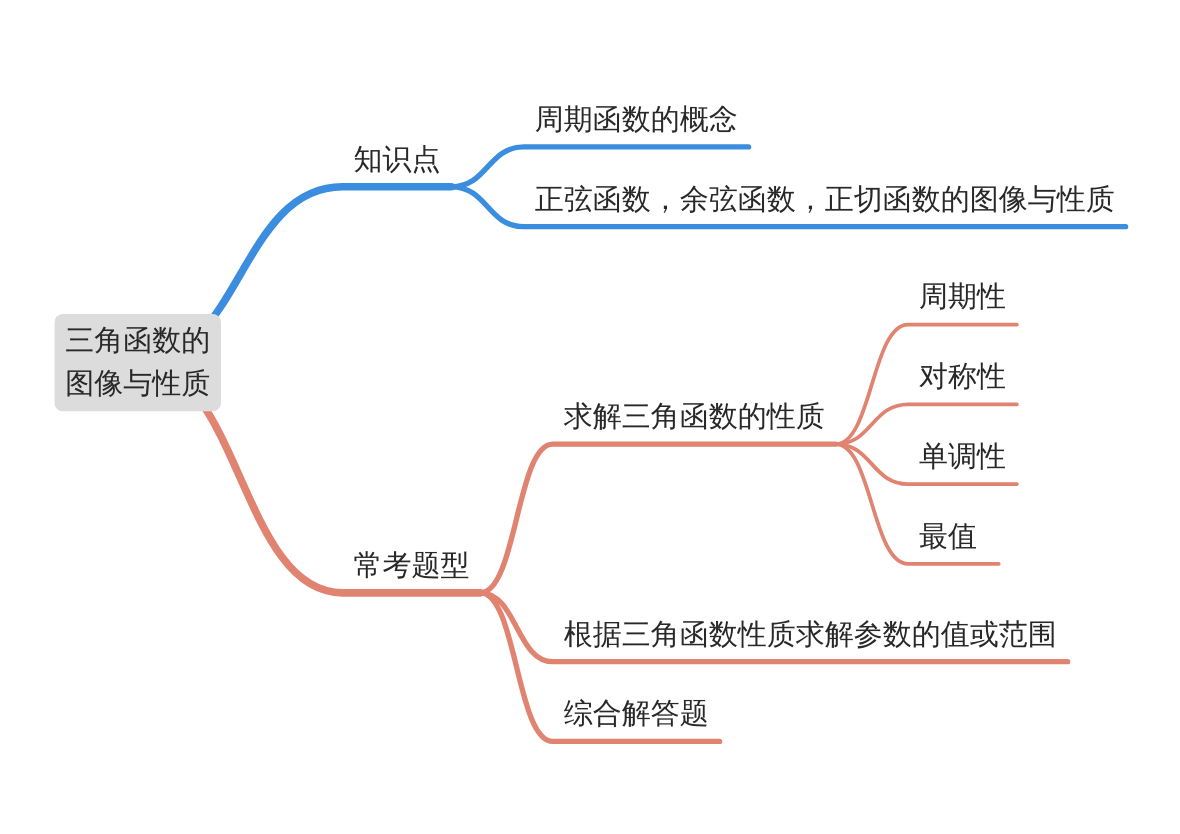
知识剖析
周期函数
一般地,对于函数\(f(x)\),如果存在一个非零常数\(T\),使得定义域内的每一个\(x\)值,都满足\(f(x+T)=f(x)\),那么函数\(f(x)\)就叫做周期函数,\(T\)叫做该函数的周期.
\({\color{Red} {PS }}\)
①从解析式\(f(x+T)=f(x)\)来看:任一自变量\(x\)对应函数值\(y\)与\(x\)增加\(T\)后对应函数值相等;
②从图象看:整体函数图象是由一部分图象像“分身术”一样向两边延申,而那一部分图象的水平长度就是其正周期!
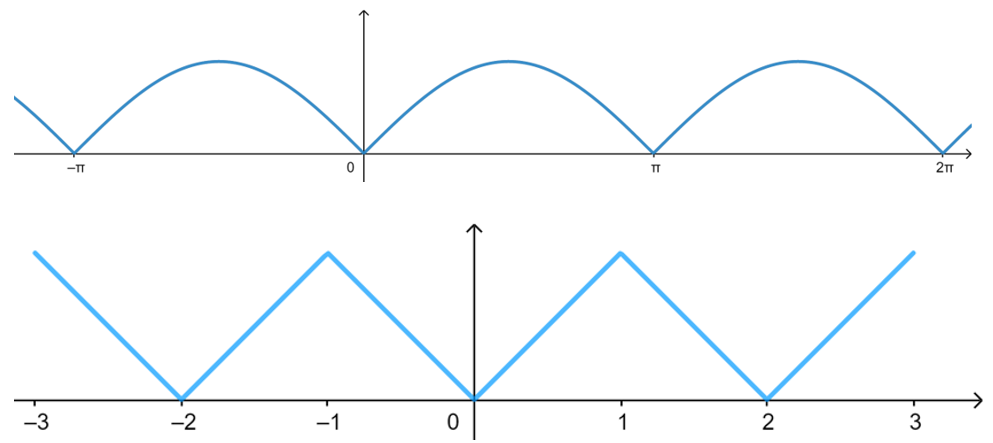
③ 三角函数就是典型的周期函数.
正弦函数,余弦函数的图像与性质
\({\color{Red} { 注}}\) 表中的\(k∈Z\)
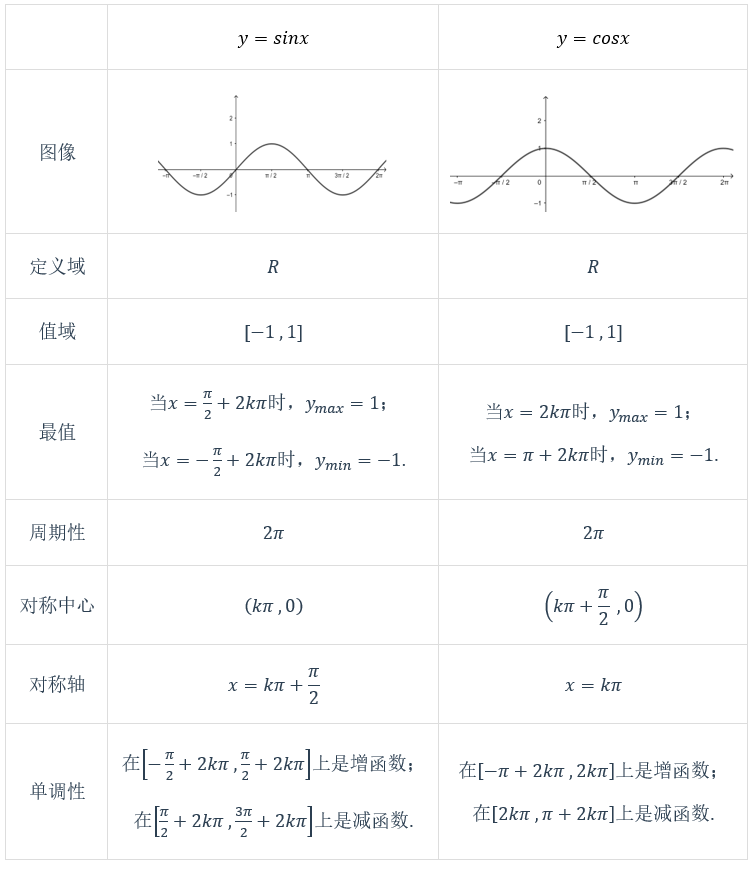
正切函数的图像与性质
\({\color{Red} {注}}\) 表中的\(k∈Z\)

经典例题
【题型一】求解三角函数的性质
性质1 周期性
【典题1】 \(f(x)=|\sin x|+|\cos x|\)的最小正周期是( )
A.\(\dfrac{\pi}{2}\) \(\qquad \qquad \qquad \qquad\) B.\(π\) \(\qquad \qquad \qquad \qquad\) C.\(2π\) \(\qquad \qquad \qquad \qquad\)D.\(3π\)
【解析】\(f\left(x+ \dfrac{\pi}{2}\right)=\left|\sin \left(x+\dfrac{\pi}{2}\right)\right|+\left|\cos \left(x+\dfrac{\pi}{2}\right)\right|\)\(=|\cos x|+|\sin x|=f(x)\),
故\(\dfrac{\pi}{2}\)是\(y=f(x)\)的周期,由选项可知选\(A\).
【点拨】从定义出发:存在一个非零常数\(T\),使得定义域内的每一个\(x\)值,都满足\(f(x+T)=f(x)\),则\(T\)叫做该函数的周期.
【典题2】下列函数中,最小正周期为\(\dfrac{\pi}{2}\)的是( )
A.\(y=\sin|x|\) \(\qquad \qquad\)B.\(y=\cos|2x|\)\(\qquad \qquad\) C.\(y=|\tan x|\) \(\qquad \qquad\)D.\(y=|\sin2x|\)
【解析】由图可知函数\(y=\sin|x|\)不是周期函数,故\(A\)不正确;
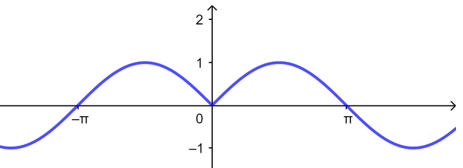
由于函数\(y=\cos|2x|=\cos2x\)的周期为\(\dfrac{2 \pi}{2}=\pi\),故\(B\)不正确;
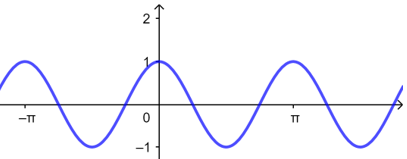
由图可知函数\(y=|\tan x|\)的周期\(T=π\),故\(C\)不正确;
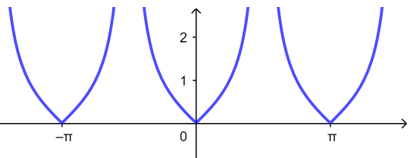
由图可知函数\(y=|\sin2x|\)的周期为\(T=\dfrac{\pi}{2}\),故\(D\)正确,
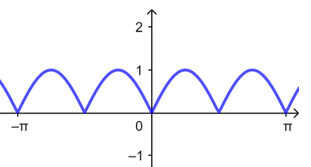
故选:\(D\).
【点拨】
① 函数\(f(x)=A\sin(ωx+φ)\), \(f(x)=A\cos(ωx+φ)\)的最小正周期\(T=\dfrac{2 \pi}{\omega}\),函数\(f(x)=A\tan(ωx+φ)\)的最小正周期\(T=\frac{\pi}{\omega}\);
② 利用函数的对称变换与翻转变换,利用图象判断函数周期更容易些.
性质2 对称性
【典题1】 函数\(y=\sin \left(2 x+\dfrac{\pi}{3}\right)\)的图象( )
A.关于点\(\left(\dfrac{\pi}{6}, 0\right)\)对称 \(\qquad \qquad \qquad \qquad\) B.关于点\(\left(\dfrac{\pi}{3}, 0\right)\)对称
C.关于直线\(x=\dfrac{\pi}{6}\)对称 \(\qquad \qquad \qquad \qquad\)D.关于直线\(x=\dfrac{\pi}{3}\)对称
【解析】 \({\color{Red} {方法1 }}\)对于函数\(y=\sin \left(2 x+\dfrac{\pi}{3}\right)\),
\({\color{Red} { (求出函数的所有对称轴和对称中心再判断)}}\)
令\(2 x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k \pi\),则\(x=\dfrac{\pi}{12}+\dfrac{k \pi}{2}\) ,
则函数的对称轴是\(x=\dfrac{\pi}{12}+\dfrac{k \pi}{2}\left(k \in Z \right)\),
若\(\dfrac{\pi}{12}+\dfrac{k \pi}{2}=\dfrac{\pi}{6}\),解得\(k=\dfrac{1}{6} \notin Z\),\(\dfrac{\pi}{12}+\dfrac{k \pi}{2}=\dfrac{\pi}{3}\),\(k=\dfrac{1}{2} \notin Z\),故排除\(C ,D\);
令\(2 x+\dfrac{\pi}{3}=k \pi\),则\(x=-\dfrac{\pi}{6}+\dfrac{k \pi}{2}\) ,
则函数的对称中心是\(\left(-\dfrac{\pi}{6}+\dfrac{k \pi}{2}, 0\right) \left(k \in Z \right)\),
若\(-\dfrac{\pi}{6}+\dfrac{k\pi}{2}=\dfrac{\pi}{6}\),解得\(k=\dfrac{2}{3}\notin Z\),可排除\(A\);
若\(-\dfrac{\pi}{6}+\dfrac{k\pi}{2}=\dfrac{\pi}{3}\),解得\(k=1\in Z\),故关于\((\dfrac{\pi}{3},0)\)对称.
\({\color{Red} { 方法2}}\) 对于函数\(y=\sin \left(2 x+\dfrac{\pi}{3}\right)\),
当\(x=\dfrac{\pi}{6}\)时,\(2 x+\dfrac{\pi}{3}=\dfrac{2 \pi}{3}\),而\(\left(\dfrac{2 \pi}{3}, 0\right)\)不是正弦函数\(y=\sin x\)的对称中心,故\(A\)错误;
当\(x=\dfrac{\pi}{3}\)时,\(2 x+\dfrac{\pi}{3}=\pi\),而是正弦函数\(y=\sin x\)的对称中心,故\(B\)正确;
当\(x=\dfrac{\pi}{6}\)时,\(2 x+\dfrac{\pi}{3}=\dfrac{2 \pi}{3}\),而\(x=\dfrac{2π}{3}\)不是正弦函数\(y=\sin x\)的对称轴,故\(C\)错误;
当\(x=\dfrac{\pi}{3}\)时,\(2 x+\dfrac{\pi}{3}=\pi\),而\(x=π\)不是正弦函数\(y=\sin x\)的对称轴,故\(D\)错误;
故选:\(B\).
【点拨】本题两种方法,
方法1是求出三角函数的全部对称轴或对称中心(此时把\(ωx+φ\)看成整体),再判断;
方法2是把问题转化正弦函数\(y=\sin x\)的性质判断;
对于三角函数\(f(x)=A \sin (\omega x+\varphi)+B\)
① 若\(x=x_0\)是其对称轴,则\(ωx_0+φ\)是正弦函数\(y=\sin x\)的对称轴;
② 若\((x_0,B)\)是其对称中心,则\((ωx_0+φ ,B)\)满足函数\(y=Asinx+B\)的对称中心.
对于三角函数\(f(x)=A\cos(ωx+φ)+B\)类似.
【典题2】 已知函数\(f(x)=\cos (3 x+\varphi)\left(-\frac{\pi}{2}<\varphi<\dfrac{\pi}{2}\right)\)图象关于直线\(x=\dfrac{5 \pi}{18}\)对称,则函数\(f(x)\)在区间\([0,π]\)上零点的个数为\(\underline{\quad \quad}\) .
【解析】\(∵\)函数\(f(x)=\cos(3x+φ)\)图象关于直线\(x=\dfrac{5 \pi}{18}\)对称,
\(\therefore 3 \times \dfrac{5 \pi}{18}+\varphi=k \pi\),
\({\color{Red} {(y=\cos x的对称轴是x=kπ) }}\)
\(\therefore \varphi=-\dfrac{5 \pi}{6}+k \pi, \quad k \in Z\),
由\(-\dfrac{\pi}{2}<\varphi<\dfrac{\pi}{2}\)知,\(k=1\)时,\(\varphi=\dfrac{\pi}{6}\),
故\(f(x)=\cos \left(3 x+\dfrac{\pi}{6}\right)\),
令\(f(x)=0\)得\(3 x+\dfrac{\pi}{6}=\dfrac{\pi}{2}+k \pi\),\(k∈Z\),
\(∴x=\dfrac{\pi}{9}+\dfrac{k \pi}{3}\),\(k∈Z\).
因为\(x∈[0,π]\),所以\(k=0,1,2\)时,\(\varphi=\dfrac{\pi}{9}, \dfrac{4 \pi}{9}, \dfrac{7 \pi}{9}\)满足条件,故零点有三个.
性质3 单调性
【典题1】 函数\(f(x)=3 \sin \left(\dfrac{2 \pi}{3}-2 x\right)\)的一个单调递减区间是( )
A.\(\left[\dfrac{7 \pi}{12}, \frac{13 \pi}{12}\right]\) \(\qquad \qquad \qquad \qquad\) B.\(\left[\dfrac{\pi}{12}, \dfrac{7 \pi}{12}\right]\) \(\qquad \qquad \qquad \qquad\) C.\(\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]\) \(\qquad \qquad \qquad \qquad\) D.\(\left[-\dfrac{5 \pi}{6}, \dfrac{\pi}{6}\right]\)
【解析】 \({\color{Red} {(求出函数的减区间) }}\)
解\(-\dfrac{\pi}{2}+2 k \pi \leq \dfrac{2 \pi}{3}-2 x \leq \dfrac{\pi}{2}+2 k \pi\)
得\(\dfrac{\pi}{12}-k \pi \leq x \leq \dfrac{7 \pi}{12}-k \pi(k \in \boldsymbol{Z})\),
\(k=0\)时,\(\dfrac{\pi}{12} \leq x \leq \dfrac{7 \pi}{12}\);\(k=1\)时,\(-\dfrac{11 \pi}{12} \leq x \leq-\dfrac{5 \pi}{12}\);\(k=-1\)时,\(\dfrac{13 \pi}{12} \leq x \leq \dfrac{19 \pi}{12}\),
\(\therefore\left[\dfrac{\pi}{12}, \dfrac{7 \pi}{12}\right]\)是\(f(x)\)的一个单调递减区间.
故选:\(B\).
【点拨】
① 复合函数的单调性:同增异减
函数\(f(x)=3 \sin \left(\dfrac{2 \pi}{3}-2 x\right)\)可看成\(y=3\sin u\)与\(u=\dfrac{2 \pi}{3}-2 x\)组成复合函数.
因为\(u=\dfrac{2 \pi}{3}-2 x\)是减函数,求函数\(f(x)=3 \sin \left(\dfrac{2 \pi}{3}-2 x\right)\)的减区间,则把\(\dfrac{2 \pi}{3}-2 x\)代入\(y=\sin x\)的增区间\(\left[-\dfrac{\pi}{2}+2 k \pi, \dfrac{\pi}{2}+2 k \pi\right]\)求出\(x\)的范围.
② 判断\(\left[\dfrac{7 \pi}{12}, \dfrac{13 \pi}{12}\right]\)是否\(f(x)=3 \sin \left(\dfrac{2 \pi}{3}-2 x\right)\)的一个单调递减区间,也可以采取前面判断对称性的方法.具体想法如下
\(\left[\dfrac{7 \pi}{12}, \dfrac{13 \pi}{12}\right]\)是\(f(x)=3 \sin \left(\dfrac{2 \pi}{3}-2 x\right)\)的一个单调递减区间
\(⇔\left[\dfrac{7 \pi}{12}, \dfrac{13 \pi}{12}\right]\)是\(f(x)=3 \sin \left(2 x-\dfrac{2 \pi}{3}\right)\)的一个单调递增区间
\(⇔\)由\(\dfrac{7 \pi}{12}<x<\dfrac{13 \pi}{12} \Rightarrow-\dfrac{3 \pi}{2}<\dfrac{2 \pi}{3}-2 x<-\dfrac{\pi}{2}\),而\(\left[-\dfrac{3 \pi}{2},-\dfrac{\pi}{2}\right]\)不是\(y=\sin x\)的增区间;
故\(\left[\dfrac{7 \pi}{12}, \dfrac{13 \pi}{12}\right]\)不是\(f(x)=3 \sin \left(2 x-\dfrac{2 \pi}{3}\right)\)的一个单调递增区间,不是\(f(x)=3 \sin \left(\dfrac{2 \pi}{3}-2 x\right)\)的一个单调递减区间,即选项\(A\)错误.
作某些选择题这样做会简洁些.
【典题2】若\(f(x)=\sin \left(2 x-\dfrac{\pi}{4}\right)\),则 ( )
A.\(f(1)>f(2)>f(3)\) \(\qquad \qquad \qquad \qquad\) B.\(f(3)>f(2)>f(1)\)
C.\(f(2)>f(1)>f(3)\) \(\qquad \qquad \qquad \qquad\) D.\(f(1)>f(3)>f(2)\)
【解析】\({\color{Red} { (显然选项是由函数单调性作出判断)}}\)
令\(-\dfrac{\pi}{2}+2 k \pi<2 x-\dfrac{\pi}{4}<\dfrac{\pi}{2}+2 k \pi\),
解得\(-\dfrac{\pi}{8}+k \pi<x<\dfrac{3 \pi}{8}+k \pi(k \in Z)\),
故\(f(x)=\sin \left(2 x-\dfrac{\pi}{4}\right)\)在\(\left[-\dfrac{\pi}{8}, \dfrac{3 \pi}{8}\right]\)上递增,
由函数的周期性易得函数在\(\left[\dfrac{3 \pi}{8}, \dfrac{7 \pi}{8}\right]\)上递增,关于\(x=\dfrac{7 \pi}{8}\)对称,
\({\color{Red} {(由于1,2,3在[\dfrac{\pi}{2}, \pi]内,需要了解函数在其附近的单调性,相当数形结合的思路)}}\)
其中\(3\)比\(2\)离对称轴\(x=\dfrac{7 \pi}{8}\)更近些,
所以\(f(3)<f(2)<0\),而\(f(1)\)接近\(1\),
所以\(f(1)>f(2)>f(3)\).
故选:\(A\).
性质4 最值
【典题1】 若函数\(f(x)=\cos \left(\omega x-\dfrac{\pi}{3}\right)(\omega>0)\)的最小正周期为\(\dfrac{\pi}{2}\),则\(f(x)\)在\(\left[0, \dfrac{\pi}{4}\right]\)上的值域为\(\underline{\quad \quad}\).
【解析】依题意得\(\dfrac{2 \pi}{\omega}=\dfrac{\pi}{2}\),\(∴ω=4\).
\(\because x \in\left[0, \dfrac{\pi}{4}\right]\),\(\therefore 4 x-\dfrac{\pi}{3} \in\left[-\dfrac{\pi}{3}, \dfrac{2 \pi}{3}\right]\),
\(\therefore \cos \left(4 x-\dfrac{\pi}{3}\right) \in\left[-\dfrac{1}{2}, 1\right]\),
即\(f(x)\)的值域是\(\left[-\dfrac{1}{2}, 1\right]\).
【典题2】已知函数\(f(x)=2 \cos \left(2 x-\dfrac{\pi}{3}\right)\)在\(\left[a-\dfrac{\pi}{4}, a\right](a \in \boldsymbol{R})\)上的最大值为\(y_1\),最小值为\(y_2\),则\(y_1-y_2\)的取值范围是\(\underline{\quad \quad}\).
【解析】函数\(f(x)=2 \cos \left(2 x-\dfrac{\pi}{3}\right)\)的周期为\(π\),
且对称轴为\(x=\dfrac{\pi}{6}+\dfrac{k \pi}{2}\),对称中心\(\left(\dfrac{5 \pi}{12}+k \pi, 0\right)\),\(k∈Z\),
\(f(x)\)的图象大致如图所示;
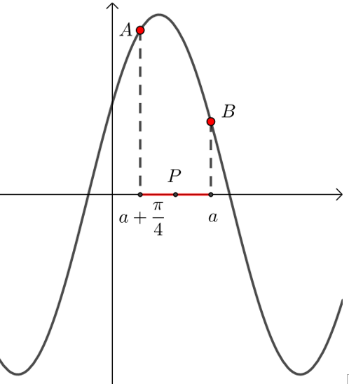
区间\(\left[a-\dfrac{\pi}{4}, a\right]\)正好是函数\(\dfrac{1}{4}\)个周期,在一个周期内讨论就行,
设\(\left[a-\dfrac{\pi}{4}, a\right]\)的中点为\(P\),
由图可知,
当点\(P\)落在对称轴上,即\(a-\dfrac{\pi}{8}=\dfrac{\pi}{6}\)时,\(y_1=2\),\(y_{2}=\sqrt{2}\),
此时\(y_1-y_2\)取得最小值为\(2-\sqrt{2}\);
当点\(P\)落在对称中心上,即\(a-\dfrac{\pi}{8}=\dfrac{5 \pi}{12}\)时,\(y_1=\sqrt{2}\),\(y_{2}=-\sqrt{2}\),
此时\(y_1-y_2\)的值为\(2 \sqrt{2}\);
\(∴y_1-y_2\)的取值范围是\([2-\sqrt{2}, 2 \sqrt{2}]\).
【点拨】
① 对于正弦函数、余弦函数,由图可知,相对而言靠近对称轴位置,函数值变化较慢,而靠近对称中心位置函数值变化较快些.
② 本题也属于“纵向距”问题,数形结合处理恰当.
巩固练习
1(★)下列函数中最小正周期为\(π\)的函数是( )
A.\(y=\sin x\) \(\qquad \qquad\)B.\(y=\cos \dfrac{1}{2} x\) \(\qquad \qquad\)C.\(y=\tan2x\) \(\qquad \qquad\)D.\(y=|\sin x|\)
2(★)下列函数中,关于直线\(x=-\dfrac{\pi}{6}\)对称的是( )
A.\(y=\sin \left(x+\dfrac{\pi}{3}\right)\)\(\qquad \qquad \qquad \qquad\) B.\(y=\sin \left(2 x+\dfrac{\pi}{3}\right)\)
C.\(y=\cos \left(x+\dfrac{\pi}{3}\right)\)\(\qquad \qquad \qquad \qquad\) D.\(y=\cos \left(2 x+\dfrac{\pi}{3}\right)\)
3(★)设函数\(f(x)=\cos \left(2 x-\dfrac{\pi}{3}\right)\),则下列结论错误的是( )
A.\(f(x)\)的一个周期为\(-π\)
B.\(y=f(x)\)的图象关于直线\(x=\dfrac{2 \pi}{3}\)对称
C.\(f\left(x+\dfrac{\pi}{2}\right)\)的一个零点为\(x=-\dfrac{\pi}{3}\)
D.\(f(x)\)在区间\(\left[\dfrac{\pi}{3}, \dfrac{\pi}{2}\right]\)上单调递减
4(★)下列函数中,以\(π\)为周期且在区间\(\left(\dfrac{\pi}{2}, \pi\right)\)单调递增的是( )
A.\(f(x)=|\cos2x|\) \(\qquad \qquad\) B.\(f(x)=|\sin2x|\)\(\qquad \qquad\) C.\(f(x)=|\cos x|\) \(\qquad \qquad\)D.\(f(x)=|\sin x|\)
5(★) 关于函数\(f(x)=|\tan x|\)的性质,下列叙述不正确的是( )
A.\(f(x)\)的最小正周期为\(\dfrac{\pi}{2}\)
B.\(f(x)\)是偶函数
C.\(f(x)\)的图象关于直线\(x=\dfrac{k \pi}{2}(k \in \mathbf{Z})\)对称
D.\(f(x)\)在每一个区间\(\left(k \pi, k \pi+\dfrac{\pi}{2}\right)(k \in \boldsymbol{Z})\)内单调递增
6(★★) 下列函数中,以\(2π\)为周期,\(x=\dfrac{\pi}{2}\)为对称轴,且在\(\left(0, \dfrac{\pi}{2}\right)\)上单调递增的函数是( )
A.\(y=2|\sin x|+\sin x\) \(\qquad \qquad \qquad \qquad\) B.\(y=2 \cos \left(x+\dfrac{\pi}{2}\right)\)
C.\(y=\sin \left(2 x-\dfrac{\pi}{2}\right)\)\(\qquad \qquad \qquad \qquad\)D.\(y=\tan \left(\dfrac{x}{2}+\dfrac{\pi}{4}\right)\)
7 (★★) 已知直线\(x=x_1 ,x=x_2\)分别是曲线\(f(x)=2 \sin \left(x+\dfrac{\pi}{3}\right)\)与\(g(x)=-\cos x\)的对称轴,则\(f(x_1-x_2)=\)( )
A.\(2\) \(\qquad \qquad \qquad \qquad\) B.\(0\) \(\qquad \qquad \qquad \qquad\) C.\(±2\) \(\qquad \qquad \qquad \qquad\) D.\(±1\)
8 (★★)关于函数\(f(x)=|\sin x|+\cos x\)有下述四个结论:
①\(f(x)\)是周期函数;
②\(f(x)\)的最小值为\(-\sqrt{2}\);
③\(f(x)\)的图象关于\(y\)轴对称;
④\(f(x)\)在区间\(\left(\dfrac{\pi}{4}, \dfrac{\pi}{2}\right)\)单调递增.
其中所有正确结论的编号是( )
A.①② \(\qquad \qquad \qquad \qquad\)B.①③ \(\qquad \qquad \qquad \qquad\)C.②③\(\qquad \qquad \qquad \qquad\) D.②④
9(★★★)已知函数\(f(x)=\sin (\omega x+\varphi)\)\(\left(\omega>0,0<\varphi<\dfrac{\pi}{2}\right)\)的最小正周期为\(π\),且关于\(\left(-\dfrac{\pi}{8}, 0\right)\)中心对称,则下列结论正确的是( )
A.\(f(1)<f(0)<f(2)\) \(\qquad\)B.\(f(0)<f(2)<f(1)\) \(\qquad\) C.\(f(2)<f(0)<f(1)\) \(\qquad\) D.\(f(2)<f(1)<f(0)\)
10(★★★)已知\(f(x)=\sin(ωx+φ)(ω>0,0<φ≤π)\)是\(R\)上的奇函数,若\(f(x)\)的图象关于直线\(x=\dfrac{\pi}{4}\)对称,且\(f(x)\)在区间\(\left[-\dfrac{\pi}{22}, \dfrac{\pi}{11}\right]\)内是单调函数,则\(f\left(\dfrac{\pi}{6}\right)=\)( )
A.\(-\dfrac{\sqrt{3}}{2}\) \(\qquad \qquad \qquad \qquad\)B.\(-\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\)C.\(\dfrac{1}{2}\) \(\qquad \qquad \qquad \qquad\)D.\(\dfrac{\sqrt{3}}{2}\)
答案
- \(D\)
- \(D\)
- \(C\)
- \(C\)
- \(A\)
- \(A\)
- \(C\)
- \(B\)
- \(D\)
- \(A\)
【题型二】根据三角函数性质求解参数的值或范围
【典题1】 已知\(ω>0\),函数\(f(x)=\sin \left(\omega x-\dfrac{\pi}{4}\right)\)的图象在区间\(\left(\dfrac{\pi}{2}, \pi\right)\)上有且仅有一条对称轴,则实数\(ω\)的取值范围是\(\underline{\quad \quad}\).
【解析】 由\(\omega x-\dfrac{\pi}{4}=k \pi+\dfrac{\pi}{2}\),
解得\(x=\dfrac{k \pi}{\omega}+\dfrac{3 \pi}{4 \omega}\),
则\(y=f(x)\)的对称轴\(x=\dfrac{k \pi}{\omega}+\dfrac{3 \pi}{4 \omega}\),\(k∈Z\)
由\(y=f(x)\)在\(\left(\dfrac{\pi}{2}, \pi\right)\)上有一条对称轴,
则满足\(\dfrac{\pi}{2}<\dfrac{k \pi}{\omega}+\dfrac{3 \pi}{4 \omega}<\pi\),
\({\color{Red} {(存在性) }}\)
即\(k+\dfrac{3}{4}<\omega<2 k+\dfrac{3}{2}\),①
而对称轴只有一条,
则要满足\(\dfrac{(k-1) \pi}{\omega}+\dfrac{3 \pi}{4 \omega} \leq \dfrac{\pi}{2}\)
且\(\dfrac{(k+1) \pi}{\omega}+\dfrac{3 \pi}{4 \omega} \geq \pi\),
\({\color{Red} {(唯一性) }}\)
即\(2 k-\dfrac{1}{2} \leq \omega \leq k+\dfrac{7}{4}\) ②
由①②可得\(\left\{\begin{array}{l}
k+\dfrac{3}{4}<2 k+\dfrac{3}{2} \\
2 k-\dfrac{1}{2} \leq k+\dfrac{7}{4}
\end{array}\right.\),解得\(k=0,1,2\);
当\(k=0\)时,由①②可得\(\omega \in\left(\dfrac{3}{4}, \dfrac{3}{2}\right)\);
当\(k=1\)时,由①②可得\(\omega \in\left(\dfrac{7}{4}, \dfrac{11}{4}\right]\);
当\(k=2\)时,由①②可得\(\omega \in\left[\dfrac{7}{2}, \dfrac{15}{4}\right]\);
故答案为:\(\left(\dfrac{3}{4}, \dfrac{3}{2}\right) \cup\left(\dfrac{7}{4}, \dfrac{11}{4}\right] \cup\left[\dfrac{7}{2}, \dfrac{15}{4}\right]\).
【点拨】
① 本题的思路是先求出函数的对称轴,再数形结合处理;理解“有且仅有一条对称轴”,存在一条对称轴在区间内,而其左右的对称轴在区间外;
② 本题涉及到两个参数\(k\)和\(ω\),求的是\(ω\)的取值范围,方法是得到\(k\)和\(ω\)的关系式,再由\(k∈Z\)的特殊性求出\(k\)的取值(或范围),进而求\(ω\)的取值范围.
【典题2】 已知函数\(f(x)=\left|\cos \left(\omega x+\dfrac{\pi}{3}\right)\right|(\omega>0)\)在区间\(\left[-\dfrac{\pi}{3}, \dfrac{5 \pi}{6}\right]\)上单调递减,则\(ω\)的取值范围为\(\underline{\quad \quad}\).
【解析】 \(y=|\cos x|\)的单调递减区间为\(\left[k \pi, k \pi+\dfrac{\pi}{2}\right], k \in Z\),
(注 由函数\(y=|cosx|\)图象易得)
由\(k \pi \leq \omega x+\dfrac{\pi}{3} \leq k \pi+\dfrac{\pi}{2}\) ,\(k∈Z\),
得\(\dfrac{k \pi-\dfrac{\pi}{3}}{\omega} \leq x \leq \dfrac{k \pi+\dfrac{\pi}{6}}{\omega}\),
即函数\(y=f(x)\)的单调递减区间为\(\left[\dfrac{k \pi-\frac{\pi}{3}}{\omega}, \dfrac{k \pi+\frac{\pi}{6}}{\omega}\right]\),\(k∈Z\),
若\(f(x)\)在区间\(\left[-\dfrac{\pi}{3}, \dfrac{5 \pi}{6}\right]\)上单调递减,
则\(\dfrac{k \pi-\frac{\pi}{3}}{\omega} \leq-\frac{\pi}{3}\)且\(\dfrac{k \pi+\frac{\pi}{6}}{\omega} \geq \dfrac{5 \pi}{6}\),
得\(\left\{\begin{array}{l}
\omega \leq \dfrac{6}{5} k+\dfrac{1}{5} \\
\omega \leq-3 k+1
\end{array}\right.\),\(k∈Z\),
\(∵ω>0\) \(∴k\)只能取\(0\);
当\(k=0\)时,\(\left\{\begin{array}{l}
\omega \leq \dfrac{1}{5} \\
\omega \leq 1
\end{array}\right.\),即\(0<\omega \leq \dfrac{1}{5}\),
即\(ω\) 的取值范围是\(\left(0, \dfrac{1}{5}\right]\).
【点拨】本题先得到\(y=|\cos x|\)的单调减区间再由复合函数单调性得到求出\(f(x)=| \cos \left(\omega x+\dfrac{\pi}{3}\right) \mid\)的减区间\(\left[\dfrac{k \pi-\frac{\pi}{3}}{\omega}, \dfrac{k \pi+\frac{\pi}{6}}{\omega}\right]\),\(k∈Z\),根据题意肯定可得\(\left[-\dfrac{\pi}{3}, \dfrac{5 \pi}{6}\right] \subseteq\left[\dfrac{k \pi-\frac{\pi}{3}}{\omega}, \dfrac{k \pi+\frac{\pi}{6}}{\omega}\right]\).
【典题3】 已知函数\(f(x)=\sin \left(\omega x+\dfrac{\pi}{3}\right)\),\((ω>0)\)在区间\(\left[-\dfrac{2 \pi}{3}, \dfrac{5 \pi}{6}\right]\)上是增函数,且在区间\([0 ,π]\)上恰好取得一次最大值\(1\),则\(ω\)的取值范围是 ( )
A.\(\left(0, \dfrac{1}{5}\right]\) \(\qquad \qquad \qquad \qquad\) B.\(\left[\dfrac{1}{2}, \dfrac{3}{5}\right]\) \(\qquad \qquad \qquad \qquad\)C.\(\left[\dfrac{1}{6}, \dfrac{1}{5}\right]\) \(\qquad \qquad \qquad \qquad\) D.\(\left[\dfrac{1}{2}, \dfrac{5}{2}\right)\)
【解析】方法一 复合函数法
令\(u=\omega x+\dfrac{\pi}{3}\),\(-\dfrac{2 \pi}{3} \leq x \leq \dfrac{5 \pi}{6}\),
则\(-\dfrac{2 \pi}{3} \omega+\dfrac{\pi}{3} \leq u \leq \dfrac{5 \pi}{6} \omega+\dfrac{\pi}{3}\).
\(∴\)函数\(y=\sin u\)在区间\(\left[-\dfrac{2 \pi}{3} \omega+\dfrac{\pi}{3}, \dfrac{5 \pi}{6} \omega+\dfrac{\pi}{3}\right]\)上单调递增,
\(\therefore\left[-\dfrac{2 \pi}{3} \omega+\dfrac{\pi}{3}, \dfrac{5 \pi}{6} \omega+\dfrac{\pi}{3}\right] \subseteq\left[-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right]\), \(\therefore \omega \leq \dfrac{1}{5}\).
当\(0≤x≤π\)时,\(\dfrac{\pi}{3} \leq u \leq \pi \omega+\dfrac{\pi}{3}\),
\(∴\)函数\(y=\sin u\)在区间\(\left[\dfrac{\pi}{3}, \pi \omega+\dfrac{\pi}{3}\right]\)恰好取一次最大值\(1\),
\(\therefore \dfrac{\pi}{2} \leq \pi \omega+\dfrac{\pi}{3}<\dfrac{5 \pi}{2}\),\(\therefore \dfrac{1}{6} \leq \omega \leq \dfrac{13}{6}\).
综上所知\(\dfrac{1}{6} \leq \omega \leq \dfrac{1}{5}\),故选\(C\).
方法二 特殊值法
当\(\omega=\dfrac{1}{2}\)时,令\(u=\dfrac{x}{2}+\dfrac{\pi}{3}\),\(-\dfrac{2 \pi}{3} \leq x \leq \dfrac{5 \pi}{6}\),
则\(0 \leq u \leq \dfrac{3 \pi}{4}\),则函数\(y=\sin u\)在区间\(\left[0, \dfrac{3 \pi}{4}\right]\)上不单调,
\(\therefore \omega=\dfrac{1}{2}\)不合题意,排除\(BD\).
当\(\omega=\dfrac{1}{12}\)时,令\(u=\dfrac{x}{12}+\dfrac{\pi}{3}\),\(0≤x≤π\) ,
则\(\dfrac{\pi}{3} \leq u \leq \dfrac{5 \pi}{12}\),则函数\(y=\sin u\)在区间\(\left[\dfrac{\pi}{3}, \dfrac{5 \pi}{12}\right]\)取不到最大值\(1\),
\(\therefore \omega=\dfrac{1}{12}\)不合题意,排除\(A\).故选:\(C\).
【点拨】根据三角函数性质求解参数的值或范围此类问题,往往都会限制函数在某个区间上的对称轴、单调性、最值等,此时最简单的想法就是先求出该函数的全部对称轴、单调区间等,再结合函数的图象判断求出来的对称轴、单
调性等与区间端点的关系!
巩固练习
1(★★)设\(f(x)=3 \sin \left(\omega x-\dfrac{\pi}{12}\right)+1\),若\(f(x)\)在\(\left[-\dfrac{\pi}{3}, \dfrac{\pi}{6}\right]\)上为增函数,则\(ω\)的取值范围是\(\underline{\quad \quad}\).
2(★★) 已知函数\(f(x)=3 \sin \left(\omega x+\dfrac{\pi}{6}\right)\)\((\omega>0)\)在\(\left(0, \dfrac{\pi}{12}\right)\)上单调递增,则\(ω\)的最大值是\(\underline{\quad \quad}\).
3(★★) 设函数\(f(x)=\sin (\omega x+\phi)\) ,\(A>0\) ,\(ω>0\) , 若f(x)在区间\(\left[\dfrac{\pi}{6}, \dfrac{\pi}{2}\right]\)上单调,且\(f\left(\dfrac{\pi}{2}\right)=f\left(\dfrac{2 \pi}{3}\right)=-f\left(\dfrac{\pi}{6}\right)\),则\(f(x)\)的最小正周期为\(\underline{\quad \quad}\).
4(★★★)已知函数\(f(x)=\sin (\omega x+\varphi)(\omega>0)\)满足\(f\left(\dfrac{\pi}{4}\right)=1\),\(f\left(\dfrac{\pi}{2}\right)=0\),且\(f(x)\)在区间\(\left(\dfrac{\pi}{4}, \dfrac{\pi}{3}\right)\)上单调,则\(ω\)取值的个数有\(\underline{\quad \quad}\)个.
5(★★★)已知函数\(f(x)=\cos \left(\omega x+\dfrac{\pi}{6}\right)(\omega>0)\)在区间\([0 ,π]\)上的值域为\(\left[-1, \dfrac{\sqrt{3}}{2}\right]\),则\(ω\)的取值范围为\(\underline{\quad \quad}\).
答案
- \(\left(0, \dfrac{5}{4}\right]\)
- \(4\)
- \(π\)
- \(3\)
- \(\left[\dfrac{5}{6}, \dfrac{5}{3}\right]\)
【题型三】 综合解答题
【典题1】 已知函数\(f(x)=\sin \left(2 x-\dfrac{\pi}{3}\right)\).
(1)当\(x_{1} \in\left(-\dfrac{\pi}{2},-\dfrac{\pi}{3}\right)\) ,\(x_{2} \in\left(0, \dfrac{\pi}{6}\right)\)时\(f(x_1)+f(x_2)=0\),求\(x_1-x_2\)的值;
(2)令\(F(x)=f(x)-3\),若对任意\(x\)都有\(F^2 (x)-(2+m)F(x)+2+m≤0\)恒成立,求\(m\)的最大值.
【解析】\((1)f(x_1)+f(x_2)=0\),
即为\(\sin \left(2 x_{1}-\dfrac{\pi}{3}\right)+\sin \left(2 x_{2}-\dfrac{\pi}{3}\right)=0\) ,
即有\(\sin \left(2 x_{1}-\dfrac{\pi}{3}\right)=-\sin \left(2 x_{2}-\dfrac{\pi}{3}\right)=\sin \left(\dfrac{\pi}{3}-2 x_{2}\right)\),
可得\(2 x_{1}-\dfrac{\pi}{3}=2 k \pi+\dfrac{\pi}{3}-2 x_{2}\),
或\(2 x_{1}-\dfrac{\pi}{3}=2 k \pi+\pi-\dfrac{\pi}{3}+2 x_{2}\) ,\(k∈Z\),
即有\(x_{1}+x_{2}=k \pi+\dfrac{\pi}{3}\)或\(x_{1}-x_{2}=k \pi+\dfrac{\pi}{2}\),
由\(x_{1} \in\left(-\dfrac{\pi}{2},-\dfrac{\pi}{3}\right)\) ,\(x_{2} \in\left(0, \dfrac{\pi}{6}\right)\),
可得\(x_{1}-x_{2} \in\left(-\dfrac{2 \pi}{3},-\dfrac{\pi}{3}\right)\),
可得\(x_{1}-x_{2}=-\dfrac{\pi}{2}\);
\((2)F(x)=f(x)-3\) 即\(F(x)=\sin \left(2 x-\dfrac{\pi}{3}\right)-3\),
令\(t=F(x)\),可得\(t∈[-4 ,-2]\),
对任意\(x\)都有\(F^2 (x)-(2+m)F(x)+2+m≤0\)恒成立,
即为\(t^2-(2+m)t+2+m≤0\),\(t∈[-4 ,-2]\);
则\(16+4(2+m)+2+m≤0\) ,\(4+2(2+m)+2+m≤0\),
解得\(m \leq-\dfrac{26}{5}\),即\(m\)的最大值为\(-\dfrac{26}{5}\).
【点拨】
① 若\(\sinα=\sinβ\),则\(α=2kπ+β\)或\(α=2kπ+π-β\)
② 第二问涉及恒成立问题,采取了二次函数零点的分布问题的方法即通过二次函数的图象分析便可求解.
【典题2】 已知函数\(f(x)=\sin^2x+a\cos x+a\) ,\(a∈R\).
(1) 当\(a=1\)时,求函数\(f(x)\)的最大值;
(2) 如果对于区间\(\left[0, \dfrac{\pi}{2}\right]\)上的任意一个\(x\),都有\(f(x)≤1\)成立,求\(a\)的取值范围.
【解析】(1) 当\(a=1\)时,\(f(x)=-\cos ^{2} x+\cos x+2\)\(=-\left(\cos x-\dfrac{1}{2}\right)^{2}+\dfrac{9}{4}\),
\(∵cosx∈[-1 ,1]\),
\(∴\)当\(\cos x=\dfrac{1}{2}\),
即\(x=2 k \pi \pm \dfrac{\pi}{3}(k \in Z)\)时,\([f(x)]_{\max }=\dfrac{9}{4}\).
(2) 依题得\(\sin^2x+a\cos x+a≤1\),
即\(a(\cos x+1) \leq \cos ^{2} x\)对任意\(x \in\left[0, \dfrac{\pi}{2}\right]\)恒成立.
当\(x \in\left[0, \dfrac{\pi}{2}\right]\)时,\(0≤cosx≤1\),则\(1≤cosx+1≤2\),
\(\therefore a \leq \dfrac{\cos ^{2} x}{\cos x+1}\)对任意\(x \in\left[0, \dfrac{\pi}{2}\right]\)恒成立.
令\(t=cosx+1\),则\(1≤t≤2\),
\(\therefore a \leq \dfrac{(t-1)^{2}}{t}=\dfrac{t^{2}-2 t+1}{t}=t+\dfrac{1}{t}-2\)对任意\(1≤t≤2\)恒成立,
于是\(a \leq\left(t+\dfrac{1}{t}-2\right)_{\min }\).
又\(\because t+\dfrac{1}{t}-2 \geq 0\),当且仅当\(t=1\),即\(x=\dfrac{\pi}{2}\)时取等号;
\(∴a≤0\).
【点拨】第二问涉及恒成立问题,利用了分离参数法和换元法.
巩固练习
1(★★★)已知函数\(f(x)=\sqrt{3} \sin \left(\omega x-\dfrac{\pi}{6}\right)\)(其中\(ω>0\))的图象上相邻两个最高点的距离为\(π\).
(1)求函数\(f(x)\)的图象的对称轴;
(2)若函数\(y=f(x)-m\)在\([0 ,π]\)内有两个零点\(x_1 ,x_2\) , 求\(m\)的取值范围及\(\cos(x_1+x_2)\)的值.
2(★★★)已知函数\(f(x)=\cos \left(\omega x+\dfrac{\pi}{3}\right)(\omega>0)\),图象上任意两条相邻对称轴间的距离为\(\dfrac{\pi}{2}\).
(1)求函数的单调区间和对称中心.
(2)若关于\(x\)的方程\(2 \sin^2x-m\cos x-4=0\)在\(x \in\left(0, \dfrac{\pi}{2}\right)\)上有实数解,求实数\(m\)的取值范围.
答案
- \(\text { (1) } x=\dfrac{k \pi}{2}+\dfrac{\pi}{3}, k \in Z\);
\(\text { (2) } m \in\left(-\sqrt{3},-\dfrac{\sqrt{3}}{2}\right) \cup\left(-\dfrac{\sqrt{3}}{2}, \sqrt{3}\right)\) ,\(\cos \left(x_{1}+x_{2}\right)=\dfrac{1}{2}\). - \((1)\)单调递增区间\(\left[k \pi-\dfrac{2 \pi}{3}, k \pi-\dfrac{\pi}{6}\right]\) ,单调递减区间\(\left[k \pi-\dfrac{\pi}{6}, k \pi+\dfrac{\pi}{3}\right]\),对称中心为\(\left(\dfrac{1}{2} k \pi+\dfrac{\pi}{12}, 0\right) k \in Z\),
\((2)\{m|m<-4\}\).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号