专题 恒成立与存在性问题

\(\mathbf{{\large {\color{Red} {欢迎到学科网下载资料学习}} } }\)【高分突破系列】 高二数学下学期同步知识点剖析精品讲义！
\(\mathbf{{\large {{\color{Red} {跟贵哥学数学，so \quad easy！}} }}}\)

适合高二同步拔高或高三专题复习，难度4颗星！

模块导图

知识剖析

恒成立问题、存在性问题归根到底是最值问题.

恒成立问题

\((1)∀x∈D\)，\(f(x)≥0\)恒成立\(\Leftrightarrow\)在\(D\)上的\(f(x)_{min}≥0\)；
\((2)∀x∈D\)，\(f(x)≤0\)恒成立 \(\Leftrightarrow\)在\(D\)上的\(f(x)_{max}≤0\)；
 

存在性问题

\((1)∃x∈D\)，\(f(x)≥0\)恒成立\(\Leftrightarrow\)在\(D\)上的\(f(x)_{max}≥0\)；
\((2)∃x∈D\)，\(f(x)≤0\)恒成立\(\Leftrightarrow\)在\(D\)上的\(f(x)_{min}≤0\)；
 

双变量存在—恒成立问题

\((1)∀x_1∈D\)，\(∀x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{min}≥g(x)_{max}\)；
\((2)∀x_1∈D\)，\(∃x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{min}≥g(x)_{min}\)；
\((3)∃x_1∈D\)，\(∀x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{max}≥g(x)_{max}\)；
\((4)∃x_1∈D\)，\(∃x_2∈E\)，\(f(x_1 )≥g(x_2)\)恒成立\(\Leftrightarrow f(x)_{max}≥g(x)_{min}\)；
 

常见处理方法

方法1 直接构造函数法：求\(f(x)≥g(x)\)恒成立\(⇔h(x)=f(x)-g(x)≥0\)恒成立.
方法2 分离参数法：求\(f(x)≥a\cdot g(x)\) (其中\(g(x)>0)\)恒成立\(\Leftrightarrow a \leq \dfrac{f(x)}{g(x)}\)恒成立.
方法3 变更主元：题型特征(已知谁的范围把谁作为主元)；
方法4 数形结合法：求\(f(x)-g(x)≥0\)恒成立\(⇔\)证明\(y=f(x)\)在\(y=g(x)\)的上方；
方法5 同构法：对不等式进行变形，使得不等式左右两边式子的结构一致，再通过构造的函数单调性进行求解；
方法6 放缩法：利用常见的不等式或切线放缩或三角函数有界性等手段对所求不等式逐步放缩达到证明所求不等式恒成立的目的；
学习各种方法时，要注意理解它们各自之间的优劣性，有了比较才能快速判断某种题境中采取哪种方法较简洁，建议学习时一题多解，多发散思考.
 

经典例题

【题型一】 单变量存在--恒成立问题

方法1 直接构造函数法与分离参数法

以下通过几题让大家感觉下直接构造函数法与分离参数法的优劣性！
【典题1】 若\(a \ln x+\dfrac{1}{2} x^{2}-(1+a) x \geq 0\)恒成立，求\(a\)的取值范围.
【解析】 \({\color{Red} { 方法一 分离参数法 }}\)
\(\operatorname{aln} x+\dfrac{1}{2} x^{2}-(1+a) x \geq 0 \Leftrightarrow a(\ln x-x) \geq x-\dfrac{1}{2} x^{2}\)，
而\(∵lnx-x<0 (x>0)\)这不难证明，
\({\color{Red} {(确认lnx-x正负，它会影响不等号方向是否改变，若不确定要分类讨论) }}\)
\(\therefore \forall x>0, a \leq \dfrac{x-\dfrac{1}{2} x^{2}}{\ln x-x}\)恒成立，
设\(f(x)=\dfrac{x-\dfrac{1}{2} x^{2}}{\ln x-x}\)，
\({\color{Red} {(分离参数成功，只需求f_{min}的最小值)}}\)
\(f^{\prime}(x)=\dfrac{(x-1)(x+2-2 \ln x)}{2(\ln x-x)^{2}}\)，
\({\color{Red} {(分析f(x)单调性⇒分析y=(x-1)(x+2-2lnx)正负性⇒分析x+2-2lnx的正负性)}}\)
令\(h(x)=x+2-2lnx\)，
则\(h^{\prime}(x)=1-\dfrac{2}{x}=\dfrac{x-2}{x}\)，
当\(0<x<2\)时，\(h'(x)<0\)，\(h(x)\)递减；
当\(x>2\)时，\(h'(x)>0\)，\(h(x)\)递增；
\(∴h(x)\)在\(x=2\)处取到最小值\(h(2)=4-2ln2>0\)，
即\(h(x)≥h(2)>0\).
\(∴x+2-2lnx>0\).
\({\color{Red} {(则y=(x-1)(x+2-2lnx)的正负性就由y=x-1确定)}}\)
那当\(0<x<1\)时，\(f'(x)<0\)，\(f(x)\)递减；
当\(x>1\)时，\(f'(x)>0\)，\(f(x)\)递增；
\(\therefore f(x) \geq f(1)=-\dfrac{1}{2}\)，\(\therefore a \leq-\dfrac{1}{2}\).
\({\color{Red} {方法二：直接构造函数法 }}\)
令\(g(x)=\operatorname{aln} x+\dfrac{1}{2} x^{2}-(1+a) x\)，定义域是\((0,+∞)\)，
\({\color{Red} { (问题可以转化为求g_{min})}}\)
\(g^{\prime}(x)=\dfrac{a}{x}+x-(1+a)=\dfrac{x^{2}-(1+a) x+a}{x}=\dfrac{(x-1)(x-a)}{x}\)，
①若\(a<0\)时，
当\(0<x<1\)时，\(g'(x)<0\)，\(g(x)\)递减；
当\(x>1\)时，\(g'(x)>0\)，\(g(x)\)递增；
即\(g(x)_{\min }=g(1)=-a-\dfrac{1}{2}\)，
若\(a \ln x+\dfrac{1}{2} x^{2}-(1+a) x \geq 0\)恒成立，
则\(-a-\dfrac{1}{2} \geq 0\)，解得\(a \leq-\dfrac{1}{2}\)，
\(\therefore a \leq-\dfrac{1}{2}\)，
② 若\(a>0\)时，\(g(1)=-a-\dfrac{1}{2}<0\)，
那\(a\ln x+\dfrac{1}{2} x^{2}-(1+a) x \geq 0\)不可能恒成立；
综上\(a \leq-\dfrac{1}{2}\).
【点拨】
①方法一分类参数法，把问题转化为不含参函数的最值问题，是大家乐见的.但注意点有二，其一\(lnx-x<0\)的证明，它的正负确定不等号方向要变号，若不确定要分类讨论运算量也不小；其二分离后得到\(f(x)=\dfrac{x-\dfrac{1}{2} x^{2}}{\ln x-x}\)，挺复杂的函数，故分离参数后得到函数比较复杂的(求导难、要多次求导等)，可考虑下是否使用分离参数法；
② 方法二直接构造函数法，它的问题在于函数含参，意味着大多数情况要分类讨论，这是大家头疼之处.本题属于导函数是“二次函数”型，研究单调性时的分类讨论略显麻烦，但“若\(a>0\)时，\(f(1)=-a-\dfrac{1}{2}<0\)”这点若看到，避免陷入较大运算量了.
 

【典题2】已知函数\(f(x)=e^x-ax-1\)．
(1)当\(a=1\)时，求\(f(x)\)的极值；
(2)若\(f(x)≥x^2\)在\([0 ,+∞)\)上恒成立，求实数\(a\)的取值范围．
【解析】 (1)过程略，函数\(f(x)\)有极小值\(f(0)=0\)，无极大值；
(2) \({\color{Red} {方法一 分类参数法 }}\)
因为\(f(x)≥x^2\)在\([0 ,+∞)\)上恒成立，
所以\(e^x-x^2-ax-1≥0\)在\([0 ,+∞)\)上恒成立，
当\(x=0\)时，\(0≥0\)恒成立，此时\(a∈R\)，
当\(x>0\)时，\(a \leq \dfrac{e^{x}-x^{2}-1}{x}\)\(在\)\((0 ,+∞)\)上恒成立，
令\(g(x)=\dfrac{e^{x}-x^{2}-1}{x}\)，
则\(g^{\prime}(x)=\dfrac{(x-1)\left(e^{x}-x-1\right)}{x^{2}}\)，
由(1)知，当\(x>0\)时，\(f(x)>0\)，
即\(e^x-x-1>0\)；
当\(0<x<1\)时，\(g'(x)<0\)，当\(x>1\)时，\(g'(x)>0\)，
所以\(g(x)\)在\((0 ,1)\)上单调递减，在\((1 ,+∞)\)上单调递增，
所以当\(x=1\)时，\(g(x)_{min}=e-2\)，
所以\(a≤e-2\)，
综上，实数\(a\)的取值范围是\((-∞ ,e-2]\)．
\({\color{Red} {方法二 直接构造函数法}}\)
\(f(x)≥x^2\)在\([0 ,+∞)\)上恒成立
等价\(e^x-x^2-ax-1≥0\)在\([0 ,+∞)\)上恒成立
令\(g(x)=e^x-x^2-ax-1\)，
则\(g^{\prime}(x)=e^x-2x-a\)，
此时很难分析导函数\(y=g^{\prime}(x)\)的正负性，故很难求原函数\(g(x)\)的最小值.
【点拨】本题利用分类参数较好的完成，难度不大，而直接构造函数法由于含参导致分类讨论难而难产了！
 

【典题3】设\(f(x)=x(e^x-1)-ax^2\)，
(1)若\(a=\dfrac{1}{2}\)，求\(f(x)\)的单调区间；
(2)若当\(x≥0\)时，\(f(x)≥0\)恒成立，求\(a\)的取值范围.
【解析】 (1)略
(2) \({\color{Red} {方法一 直接构造函数法 }}\)
\(f(x)=x(e^x-1)-ax^2=x(e^x-1-ax)\)；
当\(x≥0\)时，\(f(x)≥0\)恒成立
\(\Leftrightarrow\)\(当\)\(x≥0\)\(时，\)\(e^x-1-ax≥0\)恒成立；
令\(g(x)=e^x-1-ax\)，则\(g^{\prime}(x)=e^{x}-a\)
\({\color{Red} {(下面就导函数g'(x)是否存在零点，分a>0和a≤0讨论，若有零点，又根据零点lna与定义域端点0的大小比较， }}\)
\({\color{Red} {分0<a≤1和a>1讨论) }}\)
(1) 当\(a≤0\)时，\(g'(x)=e^x-a>0\)，\(g(x)\)递增，\(g(x)≥g(0)=0\)，满足题意；

(2) 当\(a>0\)时，令\(g'(x)=e^x-a=0\)，解得\(x=lna\)，
①若\(lna≤0\)，即\(0<a≤1\)时，在\(x∈[0,+∞)\)上\(g'(x)=e^x-a>0\)，\(g(x)\)递增，
\(g(x)≥g(0)=0\)，满足题意；

②若\(lna>0\)，即\(a>1\)时，
当\(0<x<lna\)时，\(g'(x)<0\)，\(g(x)\)递减，而\(g(0)=0\)，\(g(x)<0\)，不满足题意；

综上，\(a≤1\).

\({\color{Red} {方法二 分类参数法 }}\)
\(f(x)=x(e^x-1)-ax^2=x(e^x-1-ax)\)；
当\(x=0\)时，不等式显然恒成立；
当\(x>0\)时，\(f(x)≥0\)恒成立
\(⇔\)当\(x>0\)时，\(e^x-1-ax>0\)恒成立
\(⇔\)当\(x>0\)时，\(a<\dfrac{e^{x}-1}{x}\)恒成立
令\(h(x)=\dfrac{e^{x}-1}{x}\)，则\(h^{\prime}(x)=\dfrac{x e^{x}-e^{x}+1}{x^{2}}\)
令\(g(x)=xe^x-e^x+1\)，
则\(g'(x)=xe^x\)， \({\color{Red} {(二次求导) }}\)
\(∵x>0\)，\(∴g'(x)=xe^x>0\)，
\(∴g(x)=xe^x-e^x+1\)在\(x>0\)上递增，
即\(g(x)>g(0)=0\)，
\(∴\)当\(x>0\)时，\(h^{\prime}(x)>0\)，\(h(x)\)递增，\(∴h(x)>h(0)\)，
然而\(x\)取不到\(0\)，\(h(0)\)是没意义的，
即\(h(x)=\dfrac{e^{x}-1}{x}\)在\((0,+∞)\)上没有最小值.
这时要用到高等数学知识--- \({\color{Red} {洛必达法则 }}\) ，
\({\color{Red}{\lim \limits_{x \rightarrow 0} \dfrac{e^{x}-1}{x}=\lim \limits_{x \rightarrow 0} e^{x}=1} }\)
即当\(x⟶0\)，\(h(x)=\dfrac{e^{x}-1}{x} \rightarrow 1\)，
所以\(a≤1\).
我们可以看看\(h(x)=\dfrac{e^{x}-1}{x}\)函数图象，

【点拨】
① 本题直接构造方法较分类参数法由于分类讨论解答过程显得复杂些，但分类参数法容易跳进陷阱，\(h(x)=\dfrac{e^{x}-1}{x}\)在\((0,+∞)\)上没有最小值，最终使用了高等数学知识--洛必达法则才解决，这在高考解答题慎用；
② 那不用洛必达法则有木有其他方法呢？还是有的，用导数的定义，
求 \(\lim \limits_{x \rightarrow 0} \dfrac{e^{x}-1}{x}\)，
设\(f(x)=e^x\)，则\(f^{\prime}(x)=e^x\)，
\({\color{Red}{\lim \limits_{x \rightarrow 0} \dfrac{e^{x}-1}{x}=\lim\limits _{x \rightarrow 0} \dfrac{e^{x}-e^{0}}{x-0}} }{\color{Red}{=\lim \limits_{x \rightarrow 0} \dfrac{f(x)-f(0)}{x-0}=f^{\prime}(0)=e^{0}=1} }\)，
与洛必达法则结果一致.
③ 分离参数法有时候会遇到这种情况，思考难度就增大了！

通过以上三题，你可以总结下直接构造函数法和分类参数法的优劣性么？
 

巩固练习

1 (★★)已知函数\(f(x)=e^x+ax\)，当\(x≥0\)时，\(f(x)≥0\)恒成立，则\(a\)的取值范围为 \(\underline{\quad \quad}\) .
 
2(★★)已知函数\(f(x)=\dfrac{1+\ln (1+x)}{x}(x>0)\)，若\(f(x)>\dfrac{k}{x+1}\)恒成立，则整数\(k\)的最大值为 \(\underline{\quad \quad}\) .
 

3 (★★)已知函数\(f(x)=xlnx\)．
(1)求\(f(x)\)的最小值；
(2)若对所有\(x≥1\)都有\(f(x)≥ax-1\)，求实数\(a\)的取值范围．
 
 
4 (★★)已知函数\(f(x)=(x^2-1)e^x\)，其中\(a∈R\)．
(1)求函数\(f(x)\)在\(x=0\)处的切线方程；
(2)\(∀x≥0\)，\(f(x)≥ax-1\)，求实数\(a\)的取值范围．
 
 

5 (★★★)已知函数\(f(x)=(m-lnx)x \quad (x>1)\)．
(1)讨论\(f(x)\)的单调性；
(2)若\(f(x)-2x-m<0\)恒成立，求正整数\(m\)的最大值．参考数据：\(ln5≈1.61\)．
 
 

6 (★★★)已知函数\(f(x)=\dfrac{e^{a x}}{b x}\)在\(x=1\)处取得极值\(e\)．
(1)求函数\(f(x)\)的单调区间；
(2)若不等式\(kx+lnx≤x^2 f(x)-1\)在\((0 ,+∞)\)上恒成立，求实数\(k\)的取值范围．
 
 

参考答案

1. \([-e ,+∞)\)

2. \(3\)

3. \((1)-\dfrac{1}{e}\quad (2) a \leq 1\)

4. \((1) x+y+1=0 \quad (2) a≤-1\)

5. \((1)\)当\(m≤1\)时，\(f(x)\)在\((1 ,+∞)\)上单调递减；当\(m>1\)时，\(f(x)\)在\((1 ,e^{m-1})\)上单调递增，在\((e^{m-1},+∞)\)上单调递减；
   \((2)4\)

6. \((1)f(x)\)的单调递增区间是\((1,+∞)\),单调递减区间是\((-∞,0)\)和\((0,1)\)；
   \((2)k≤1\).
    

方法2 变更主元法

【典题1】 若不等式\(mx^2-2x+1-m<0\)对满足\(-2≤m≤2\)的所有\(m\)都成立，求\(x\)的取值范围．
【解析】 原不等式可化为\((x^2-1)m-(2x-1)<0\)，
构造函数\(f(m)=(x^2-1)m-(2x-1)(-2≤m≤2)\)，其图象是一条线段\(l\)．
若要满足题意，则线段l要在\(x\)轴下方，

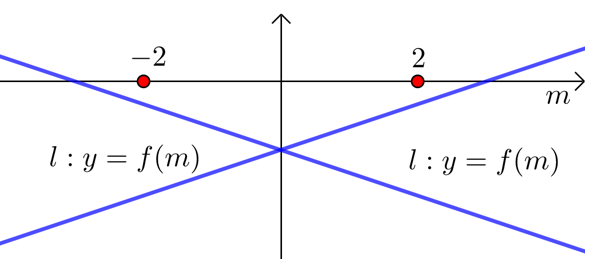
只需\(\left\{\begin{array}{l} f(-2)=-2\left(x^{2}-1\right)-(2 x-1)<0 \\ f(2)=2\left(x^{2}-1\right)-(2 x-1)<0 \end{array}\right.\) ，
即\(\left\{\begin{array}{l} 2 x^{2}+2 x-3>0 \\ 2 x^{2}-2 x-1<0 \end{array}\right.\)，解得\(\dfrac{-1+\sqrt{7}}{2}<x<\dfrac{1+\sqrt{3}}{2}\)．
【点拨】
① 我们平时习惯上把x当作自变量，记函数\(y=mx^2-2x+1-m\)，而知道的是参数\(m\)的范围\([-2,2]\)，求自变量\(x\)的范围，这就是比较别扭了.若把\(x\)与\(m\)两个量互换一下角色，即将\(m\)视为变量，\(x\)为常量，来个“反客为主”，则上述问题可转化为关于\(m\)的一次函数在\([-2,2]\)内小于\(0\)恒成立的问题，结合图象便可解决.
② 对于该题型，题目给出谁的范围就拿谁作为自变量，另一个视为参数处理.
 

巩固练习

1(★★)已知定义在\(R\)上的函数\(f(x)=ax^3-2ax^2+b(a>0)\)在区间\([－2 ,1]\)上的最大值是\(5\)，最小值是\(－11\)．
(1)求函数\(f(x)\)的解析式；
(2)若\(t∈[－1 ,1]\)时，\(f'(x)+tx≤0\)恒成立，求实数\(x\)的取值范围．
 
 

2(★★★)设函数\(y=f(x)\)在区间\(D\)上的导数为\(f'(x)\)，\(f'(x)\)在区间\(D\)上的导数为\(g(x)\)，若在区间\(D\)上，\(g(x)<0\)恒成立，则称函数\(y=f(x)\)在区间\(D\)上为“凸函数”，已知实数\(m\)是常数，\(f(x)=\dfrac{x^{4}}{12}-\dfrac{m x^{3}}{6}-\dfrac{3 x^{2}}{2}\).
(1)若\(y=f(x)\)在区间\([0,3]\)上为“凸函数”，求\(m\)的取值范围；
(2)若对满足\(|m|≤2\)的任何一个实数\(m\)，函数\(f(x)\)在区间\((a,b)\)上都为“凸函数”，求\(b-a\)的最大值.
 
 
 

参考答案

1. \((1) f(x)=x^3-2x^2+5 \quad (2) [0 ,1]\)
2. \((1) m>2 \quad (2) 2\)
    

方法3 数形结合法

【典题1】已知函数\(f(x)\)满足\(f(x)=f^{\prime}(1) e^{x-1}-f(0) x+\dfrac{1}{2} x^{2}\)，若\(f(x) \geq \dfrac{1}{2} x^{2}+a x+b\)，求\((a+1)b\)的最大值.
【解析】 易得\(f(x)=e^{x}-x+\dfrac{1}{2} x^{2}\)，
则\(f(x) \geq \dfrac{1}{2} x^{2}+a x+b \Leftrightarrow e^{x} \geq(a+1) x+b\),
即\(C:y=e^x\)的图象在\(y=(a+1)x+b\)的上方，
设曲线\(C\)与直线\(l\)相切于\(P(x_0,y_0)\)，
则切线\(l\)方程为\(y=e^{x_{0}} x+e^{x_{0}}\left(1-x_{0}\right)\)
则\(a+1=e^{x_{0}}, e^{x_{0}}\left(1-x_{0}\right) \geq b\)，
所以\((a+1) b \leq e^{x_{0}} \times e^{x_{0}}\left(1-x_{0}\right)=e^{2 x_{0}}\left(1-x_{0}\right)\)，
令\(g(x)=e^{2x} (1-x)\)，
则\(g^{\prime}(x)=e^{2x} (1-2x)\)，
易得\(g(x) \geq g\left(\dfrac{1}{2}\right)=\dfrac{e}{2}\).
当\(a=\sqrt{e}-1, b=\dfrac{\sqrt{e}}{2}\)时，\((a+1)b\)取到最大值\(\dfrac{e}{2}\).

【点拨】把\(f(x)≥0\)恒成立转化为两个函数之间的关系\(g(x)≥h(x)\)，进而想到两函数图象关系.本题把其中一函数选择一次函数(直线)，再用导数几何意义求解是常见的方法.
 

【典题2】已知函数\(f(x)=ae^x-lnx-1\)，若\(f(x)≥0\)恒成立，则实数\(a\)的取值范围是 \(\underline{\quad \quad}\) ．
【解析】 依题意，\(ae^x≥lnx+1\)对任意\(x∈(0 ,+∞)\)恒成立，
设\(g(x)=ae^x\)，\(h(x)=lnx+1\)，
则需函数\(g(x)\)的图象在函数\(h(x)\)图象的上方，
\({\color{Red} {(g(x)=ae^x (a>0)是凹函数，h(x)=lnx+1是凸函数，适合数形结合)}}\)
当\(a≤0\)时，不可能满足题意；
当\(a>0\)时，作出函数图象如下，

设函数\(g(x)\)与函数\(h(x)\)相切于点\(P(m ,n)\)，
\({\color{Red} {(共切线的处理方法)}}\)
则\(\left\{\begin{array}{l} a e^{m}=\dfrac{1}{m} \\ n=a e^{m} \\ n=\ln m+1 \end{array}\right.\)，解得\(\left\{\begin{array}{l} m=1 \\ n=1 \\ a=\dfrac{1}{e} \end{array}\right.\)，
由图可知满足条件的\(a\)的取值范围为\(\left[\dfrac{1}{e},+\infty\right)\)．
【点拨】本题构造凹函数和凸函数是常见方法.
 

巩固练习

1(★★)已知函数\(f(x)=\left(a-\dfrac{1}{2}\right) x^{2}-2 a x+\ln x\).当\(x∈(1,+∞)\)时，不等式\(f(x)<0\)恒成立，则实数\(a\)的取值范围是 \(\underline{\quad \quad}\) .
 

2(★★★) 设函数\(f(x)=lnx-mx^2+2x\)，若存在唯一的整数\(x_0\)使得\(f(x_0)>0\)，则实数\(m\)的取值范围是 \(\underline{\quad \quad}\) ．
 

3(★★★)已知\(f(x)=(e^x-a)(3ax+1)\)，若\(f(x)≥0(x∈R)\)成立，则满足条件的\(a\)的个数是 \(\underline{\quad \quad}\) ．
 

4(★★★)若\(ax+\cos x≤1+\sin x\)，\(x∈[0,π]\)，则实数\(a\)的取值范围是 \(\underline{\quad \quad}\) ．
 

参考答案

1. \(\left[-\dfrac{1}{2}, \dfrac{1}{2}\right]\)
2. \(\left[\dfrac{\ln 2}{4}+1,2\right)\)
3. \(3\)
4. \(a \leq \dfrac{2}{\pi}\)
    

方法4 同构法

【典题1】已知函数\(f(x)=e^{m x}-\dfrac{1}{m} \ln x\)，当\(x>0\)时，\(f(x)>0\)恒成立，则\(m\)的取值范围为 \(\underline{\quad \quad}\) .
【解析】 由题意，若\(m≤0\)显然\(f(x)\)不是恒大于零，故\(m>0\)．
则显然\(f(x)=e^{m x}-\dfrac{1}{m} \ln x>0\)在\((0 ,1]\)上恒成立；
当\(x>1\)时，\(f(x)=e^{m x}-\dfrac{1}{m} \ln x>0 \Leftrightarrow e^{m x}>\dfrac{1}{m} \ln x\)
\(\Leftrightarrow m x \cdot e^{m x}>x \ln x=\ln x \cdot e^{\ln x}\)，
\({\color{Red} { (注意到x=e^{lnx}) }}\)
令\(g(t)=te^t (t>0)\)，
则\(g'(t)=(1+t) e^t>0\)，\(g(t)\)在\((0 ,+∞)\)上单调递增．
因为\(mx>0\)，\(lnx>0(x>1)\)，
所以\(m x \cdot e^{m x}>\ln x \cdot e^{\ln x} \Leftrightarrow m x>\ln x\)，
即\(m>\dfrac{\ln x}{x}(x>1)\)，
再设\(h(x)=\dfrac{\ln x}{x}\Rightarrow h^{\prime}(x)=\dfrac{1-\ln x}{x^{2}}(x>1)\)，
令\(h'(x)=0\)，则\(x=e\)，
易得\(h(x)\)在\((0 ,e)\)上单调递增，在\((e ,+∞)\)上单调递减，
所以\(h(x)_{\max }=h(e)=\dfrac{1}{e}\)，故\(m>\dfrac{1}{e}\)，
所以\(m\)的取值范围为\(\left(\dfrac{1}{e},+\infty\right)\)．
 

【典题2】已知函数\(f(x)=x+a\ln x+e^{-x}-x^{a}(a<0)\)，若\(f(x)≥0\)在\(x∈[2 ,+∞)\)上恒成立，则实数\(a\)的最小值为 \(\underline{\quad \quad}\) .
【解析】 由\(f(x)≥0\)在\(x∈[2 ,+∞)\)上恒成立，
得：\(\ln x^{a}-x^{a} \geq \ln e^{-x}-e^{-x}\)在\(x∈[2 ,+∞)\)上恒成立，
\({\color{Red} {(这里注意到x=lne^x)}}\)
易知当\(x∈[2 ,+∞)\)，\(a<0\)时，
\(0<x^{a}<1\)\(，\)\(0<e^{-x}<1\)
令函数\(g(t)=lnt－t(0<t<1)\)，
则\(g^{\prime}(t)=\dfrac{1}{t}-1>0\)\(，\)\(g(t)\)单调递增，
故有\(x^{a} \geq e^{-x}\)，
则\(a\ln x \geq-x \Rightarrow a \geq-\dfrac{x}{\ln x}\)在\(x∈[2 ,+∞)\)上恒成立，
令\(F(x)=-\dfrac{x}{\ln x}(x \geq 2)\)，
则\(F^{\prime}(x)=\dfrac{1-\ln x}{(\ln x)^{2}}\)，
易得\(F(x)\)在\([2 ,e)\)上单调递增，在\([e ,+∞)\)上单调递减，
故\(F(x)_{max}=F(e)=-e\)，故\(a≥-e\).
【点拨】
① 利用同构法处理不等式，主要通过变形使得不等式左右两边结构要一致，其中懂得“整体思想”，变形的技巧有\(x=lne^x\) ,\(x=e^{lnx}\)，\(x+lnx=ln⁡(xe^x)\)，\(x e^{x}=e^{x+\ln x}\)等，最终构造的函数多是常见的超越函数\(y=xe^x\)，\(y=xlnx\)，\(y=lnx+x\)，\(y=\dfrac{e^{x}}{x}\)等.
② 同构法在另一专题再细讲.
 

巩固练习

1(★)已知\(a>0\)，若\(alnx≤xlna\)恒成立，则\(a\)的值是 \(\underline{\quad \quad}\) ．
 

2(★★★)若关于\(x\)的不等式\(e^x－alnx≥a\)恒成立，则实数\(a\)的取值范围为 \(\underline{\quad \quad}\) ．
 

3(★★)证明：\(xe^x≥x+lnx+1\)．
 
 
4(★★★)函数\(f(x)=xe^x-ax^2\)，\(g(x)=\ln x+x-x^{2}+1-\dfrac{e}{a}\)，\(a>1\)时，\(f(x)-ag(x)≥0\)恒成立，求\(a\)的范围.
 
 

参考答案

1. \(e\)
2. \([0 ,e]\)
3. 提示：同构法
4. \((0,e]\)
    

方法5 放缩法

【典题1】已知函数\(f(x)=me^x-lnx-1\)
(1)当\(m=1\)时，求曲线\(y=f(x)\)在点\((1,f(1))\)处的切线方程；
(2)当\(m≥1\)时，证明\(f(x)>1\).
【解析】 (1) 过程略，切线方程为\(y=(e-1)x\).
(2)当\(m≥1\)时，\(me^x-lnx-1≥e^x-lnx-1\)
\({\color{Red} {(由m≥1进行放缩，消去m的影响) }}\)
要证明\(f(x)>1\)，只需证明\(e^x-2>lnx\),
\({\color{Red} {(接着要用放缩法证明，先证明两个重要不等式)}}\)
先证明\(e^x≥x+1(x∈R)\)
设\(t(x)=e^x-x-1\)，则\(t^{\prime}(x)=e^x-1\)
当\(x<0\)时，\(t^{\prime}(x)<0\)，\(t(x)\)递减；
当\(x>0\)时，\(t^{\prime} (x)>0\)，\(t(x)\)递增；
所以\(t(x)≥t(0)=0\)，
即\(e^x≥x+1\)(当\(x=0\)时取到等号)
再证明\(lnx≤x-1\)，
设\(p(x)=lnx-x+1\)，则\(p^{\prime}(x)=\dfrac{1}{x}-1\)
当\(0<x<1\)时，\(p^{\prime}(x)>0\)，\(p(x)\)递增；
当\(x>1\)时，\(p^{\prime}(x)<0\)，\(p(x)\)递减；
所以\(p(x)≤p(1)=0\)，
即\(lnx≤x-1\)(当\(x=1\)时取到等号)
则由不等式\(e^x≥x+1\)和\(lnx≤x-1\)
可得\(e^x-2≥x-1≥lnx\)，
\({\color{Red} {(利用放缩法简洁地给出证明)}}\)
由于取到等号的条件不同，所以\(e^x-lnx-2>0\).
综上可知当\(m≥1\)时，证明\(f(x)>1\).
【点拨】
① 本题在两处用了放缩法，注意消化这些技巧；若对不等式\(e^x≥x+1\)和\(lnx≤x-1\)比较熟悉，本题证明思路较易看出来的，证明过程也很简洁，给人很舒服的感觉；
② 本题还有很多方法，比如直接构造函数法就涉及到“隐点问题”，方法不如放缩法.
③ 放缩法还有很多变式，这个在另一专题再讲解.
 

巩固练习

1(★★)求证:当\(n≥2\)且\(n∈N^*\)时，\(\ln n>\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}\).
 
 
2(★★★)已知函数\(f（x）=xe^x-2lnx-x^2+x-2\)．
(1)求函数\(f(x)\)图象在\(x=1\)处的切线方程；
(2)证明：\(f(x)>0\)．
 
 

3(★★★) 设函数\(f(x)=\ln x+\dfrac{a}{x-1}(a>0)\)
(1)当\(a=\dfrac{1}{30}\)时，求函数\(f(x)\)的单调区间；
(2)当\(a \geq \dfrac{1}{2}\)，\(x∈(1,+∞)\)时，求证\(\ln x+\dfrac{a}{x-1}>1\).
 
 

参考答案

1. 提示：放缩法
2. \((1) y=(2e﹣3)x﹣e+1\) \((2)\) 提示：放缩法
   3.\((1)\)递增区间\((0, \dfrac{5}{6})\),\((\dfrac{6}{5},+\infty)\)，递减区间\(\left(\dfrac{5}{6}, 1\right)\),\(\left(1, \dfrac{6}{5}\right)\)
   \((2)\)提示：放缩法
    

【题型二】双变数存在---恒成立问题

【典题1】已知两个函数\(f(x)=8x^2+16x-k\),\(g(x)=2x^3+5x^2+4x\)，其中\(k\)为实数.
(1)对任意\(x∈[-3,3]\)，都有\(f(x)≤g(x)\)成立，求\(k\)的取值范围；
(2)若对\(∀x_1∈(0,+∞)\)，总存在\(x_{2} \in\left(0, \dfrac{\pi}{2}\right)\)，使得\(f(x_1)<g(x_2)\)成立，求实数\(a\)的取值范围；
(3)对任意\(x_1,x_2∈[-3,3]\)，都有\(f(x_1 )≤g(x_2)\)，求\(k\)的取值范围.
【解析】 (1)设\(h(x)=g(x)-f(x)=2x^3-3x^2-12x+k\)
问题转化为\(x∈[-3,3]\)时，\(h(x)≥0\)恒成立，
故\(h(x)_{min}≥0\)；
易得\(h(x)_{min}≥-45+k\)，
由\(k-45≥0⇒k≥45\).
(2)据题意：存在\(x∈[-3,3]\)，使\(f(x)≤g(x)\)成立
\(⇔h(x)=g(x)-f(x)≥0\)在\(x∈[-3,3]\)有解，
易得\(h(x)_{max}=k+7\)，于是\(k≥-7\).
(3) 问题转化为\(f(x)_{max}≤g(x)_{min}\),\(x∈[-3,3]\)，
易得\(g(x)_{min}=g(-3)=-21\)，\(f(x)_{max}=f(3)=120-k\)，
则\(120-k≤-21⇒k≥141\).
【点拨】
① 第一问是恒成立问题，第二问是存在性问题，第三问是双变量成立问题；
② 第三问怎么确定\(f(x)_{max}≤g(x)_{min}\)，即到底是函数最大值还是最小值呢？
可把问题转化为第一、二问的问题，具体如下，
先把\(g(x_2)\)看成定值\(m\)，那\(∀x_1∈[-3,3]\)，都有\(f(x_1)≤m\)，当然是要\(f(x)_{max}≤m\)；
再把\(f(x_1)\)看成定值\(n\)，那\(∀x_2∈[-3,3]\)，都有\(n≤g(x_2)\)，当然是\(g(x)_{min}≥n\)；
故问题转化为\(f(x)_{max}≤g(x)_{min}\).
其他形式的双变量成立问题同理.
 

【典题2】 已知函数\(f(x)=x^2 e^{-x}\)，\(g(x)=-\dfrac{1}{3} x^{3}+2 x^{2}-3 x+c\)．若对\(∀x_1∈(0 ,+∞)\)，\(∃x_2∈[1,3]\)，使\(f(x_1)=g(x_2)\)成立，则\(c\)的取值范围是 \(\underline{\quad \quad}\) .
【解析】 \({\color{Red} {(若要满足f(x_1)=g(x_2)成立，则y=g(x)的值域包含y=f(x)的值域) }}\)
因为\(f(x)=x^2 e^{－x}\)，\(x∈(0 ,+∞)\)，
所以\(f^{\prime}(x)=\dfrac{x(2-x)}{e^{x}}\)，
令\(f'(x)=0\)，解得\(x=2\)，
故\(f(x)\)在\((0 ,2)\)递增，在\((2 ,+∞)\)递减，
故\(f(x)_{\max }=f(2)=\dfrac{4}{e^{2}}\)，
而\(x→0\)时，\(f(x)→0\)，\(x→+∞\)时，\(f(x)→+∞\)，
故\(f(x) \in\left(0, \dfrac{4}{e^{2}}\right]\)，
因为\(g(x)=-\dfrac{1}{3} x^{3}+2 x^{2}-3 x+c\)，\(g'(x)=-(x-3)(x-1)\)，
所以当\(x∈[1 ,3]\)时，\(g'(x)>0\)，
故\(g(x)\)在\([1 ,3]\)递增，
则\(g(x)_{\min}=g(1)=-\dfrac{4}{3}+c\)，\(g(x)_{max}=g(3)=c\)，
故\(g(x) \in\left[-\dfrac{4}{3}+c, c\right]\)，
若对\(∀x_1∈(0 ,+∞)\)，\(∃x_2∈[1 ,3]\)，使\(f(x_1)=g(x_2)\)成立，
则\(\left(0, \dfrac{4}{e^{2}}\right] \subseteq\left[-\dfrac{4}{3}+c, c\right]\)，
故\(\left\{\begin{array}{l} -\dfrac{4}{3}+c \leq 0 \\ \dfrac{4}{e^{2}} \leq c \end{array}\right.\)，解得：\(\dfrac{4}{e^{2}} \leq c \leq \dfrac{4}{3}\).
 

【典题3】 已知函数\(f(x)=lnx-x+1\)，\(x∈(0 ,+∞)\)，\(g(x)=\sin x-ax(a∈R)\)．
(1)求\(f(x)\)的最大值；
(2)若对\(∀x_1∈(0 ,+∞)\)，总存在\(x_{2} \in\left(0, \dfrac{\pi}{2}\right)\)，使得\(f(x_1 )<g(x_2)\)成立，求实数\(a\)的取值范围；
(3)证明不等式\(\sin \left(\dfrac{1}{n}\right)^{n}+\sin \left(\dfrac{2}{n}\right)^{n}+\cdots+\sin \left(\dfrac{n}{n}\right)^{n}<\dfrac{e}{e-1}\)(其中\(e\)是自然对数的底数)．
【解析】 (1)过程略，当\(x=1\)时\(f(x)\)取得最大值为\(f(1)=0\)；
(2)解：对\(∀x_1∈(0 ,+∞)\)，总存在\(x_{2} \in\left(0, \dfrac{\pi}{2}\right)\)，使得\(f(x_1)<g(x_2)\)成立，
等价于\(f(x)_{\max}<g(x)_{\max}\)成立，
由(1)知，\(f(x)_{\max}=0\)，
则问题等价于\(g(x)_{\max}>0\)，
因为\(g(x)=\sin x-ax\)，所以\(g'(x)=\cos x-a\)，
当\(x \in\left(0, \dfrac{\pi}{2}\right)\)时，\(cosx∈(0 ,1)\)，
\({\color{Red} {(利用三角函数的有界性) }}\)
①当\(a≥1\)时，若\(x \in\left(0, \dfrac{\pi}{2}\right)\)，\(g'(x)<0\)，\(g(x)\)单调递减，\(g(x)\)，不合题意；
②当\(0<a<1\)时，\(\exists x_{0} \in\left(0, \dfrac{\pi}{2}\right)\)，使得\(g'(x_0)=0\)，
若\(x∈(0 ,x_0)\)，\(g'(x)>0\)，若\(x \in\left(x_{0}, \dfrac{\pi}{2}\right)\)时，\(g'(x)<0\)，
即当\(g(x)_{\max}=g(x_0)>g(0)=0\)，
则\(\exists x_{2} \in\left(0, \dfrac{\pi}{2}\right)\)，使得\(g(x_2)>0\)，符合题意；
③当\(a≤0\)时，若\(x \in\left(0, \dfrac{\pi}{2}\right)\)，\(g'(x)>0\)，\(g(x)\)单调递增，\(g(x)>g(0)=0\)，
则\(\exists x_{2} \in\left(0, \dfrac{\pi}{2}\right)\)，使得\(g(x_2)>0\)，符合题意，
综上可知，所求实数\(a\)的范围是\((-∞ ,1)\)；
(3)证明：由(2)可知，
当\(a=1\)时，若\(x∈(0 ,1]\)，\(\sin x<x\)，
令\(x=\dfrac{k}{n}\left(k \leq n, k, n \in \boldsymbol{N}^{*}\right)\)，\(\left(\dfrac{k}{n}\right)^{n} \in(0,1]\)，
有\(\sin \left(\dfrac{k}{n}\right)^{n}<\left(\dfrac{k}{n}\right)^{n}\)，
再由(1)可得\(\ln x<x﹣1\)，
则\(\ln \dfrac{k}{n} \leq \dfrac{k}{n}-1=\dfrac{k-n}{n}\)，
即\(n \cdot \ln \dfrac{k}{n} \leq k-n \Rightarrow \ln \left(\dfrac{k}{n}\right)^{n} \leq k-n\)，
\(\therefore\left(\dfrac{k}{n}\right)^{n} \leq e^{k-n}\)，
\(\therefore\left(\dfrac{1}{n}\right)^{n}+\left(\dfrac{2}{n}\right)^{n}+\ldots+\left(\dfrac{n}{n}\right)^{n} \leq e^{1-n}+e^{2-n}+\ldots+e^{n-n}\)
\(=\dfrac{e^{1-n}\left(1-e^{n}\right)}{1-e}\)
\(=\dfrac{e-e^{1-n}}{e-1}<\dfrac{e}{e-1}\)
则\(\sin \left(\dfrac{1}{n}\right)^{n}+\sin \left(\dfrac{2}{n}\right)^{n}+\ldots+\sin \left(\dfrac{n}{n}\right)^{n} <\left(\dfrac{1}{n}\right)^{n}+\left(\dfrac{2}{n}\right)^{n}+\ldots+\left(\dfrac{n}{n}\right)^{n}<\dfrac{e}{e-1}\)．
\({\color{Red} {(放缩法证明，利用不等式\sin x<x和\ln x<x-1，要熟悉常见恒等式)}}\)
 

巩固练习

1(★★)已知\(1<a<4\)，函数\(f(x)=x+\dfrac{9}{x}\),\(\exists x_{1} \in[1, a]\)，\(x_{2} \in[a, 4]\)使得\(f(x_1)f(x_2)≥80\)，则\(a\)的取值范围 \(\underline{\quad \quad}\) ．
 

2(★★)已知函数\(f(x)=x+\dfrac{4}{x}\)，\(g(x)=2^x+a\)，若任意\(x_{1} \in\left[\dfrac{1}{2}, 1\right]\)，都存在\(x_2∈[2 ,3]\)，使得\(f(x_1)≥g(x_2)\)，则实数\(a\)的取值范围是 \(\underline{\quad \quad}\) ．
 

3(★★★)已知函数\(f(x)=-x|x-a|\)，若对任意的\(x_1∈(2 ,+∞)\)，都存在\(x_2∈(-1 ,0)\)，使得\(f(x_1)f(x_2)=-4\)，则实数\(a\)的最大值为 \(\underline{\quad \quad}\) ．
 

4(★★★) 已知函数\(f(x)=lnx\)，若对任意的\(x_1 ,x_2∈(0 ,+∞)\)，都有\([f(x_1)-f(x_2)](x_1^2-x_2^2)>k(x_1 x_2+x_2^2)\)恒成立，则实数\(k\)的最大值是 \(\underline{\quad \quad}\) ．
 

5(★★★)设\(f(x)=\dfrac{2 x^{2}}{x+1}\)，\(g(x)=ax+5－2a(a>0)\)．
(1)求\(f(x)\)在\(x∈[0,1]\)上的值域；
(2)若对于任意\(x_1∈[0,1]\)，总存在\(x_0∈[0,1]\)，使得\(g(x_0)=f(x_1)\)成立，求\(a\)的取值范围．
 
 

6(★★★) 设函数\(f(x)=\ln x-\dfrac{2 a}{x-1}-a\)在开区间\(\left(0, \dfrac{1}{2}\right)\)内有极值．
(1)求实数\(a\)的取值范围；
(2)若\(x_1∈(0 ,1)\) ,\(x_2=(1 ,+∞)\)．求证：\(f\left(x_{1}\right)-f\left(x_{2}\right)>2 \ln 2+\dfrac{3}{2}\)．
 
 

参考答案

1. \((1,4-\sqrt{7}]\)
2. \((－∞ ,1]\)
3. \(1\)
4. \(0\)
5. \((1) [0 ,1]\) \(\text { (2) } \dfrac{5}{2} \leq a \leq 4\)
6. \(\text { (1) }\left(-\infty,-\dfrac{1}{4}\right)\) \((2)\)略