卷积神经网络(mxnet实现)

卷积神经网络（convolutional neural network）是含有卷积层（convolutional layer）的神经网络。卷积神经网络均使用最常见的二维卷积层。它有高和宽两个空间维度，常用来处理图像数据。虽然卷积层得名于卷积（convolution）运算，但我们通常在卷积层中使用更加直观的互相关（cross-correlation）运算。在二维卷积层中，一个二维输入数组和一个二维核（kernel）数组通过互相关运算输出一个二维数组。

1.二维互相关运算

假设输入是一个高和宽均为3的二维数组。我们将该数组的形状记为3×33×3或（3，3）。核数组的高和宽分别为2。该数组在卷积计算中又称卷积核或过滤器（filter）。卷积核窗口（又称卷积窗口）的形状取决于卷积核的高和宽，即2×22×2。阴影部分为第一个输出元素及其计算所使用的输入和核数组元素：0×0+1×1+3×2+4×3=190×0+1×1+3×2+4×3=19。

 

 

 

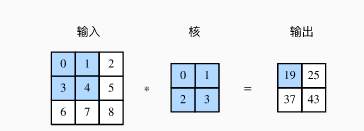
 在二维互相关运算中，卷积窗口从输入数组的最左上方开始，按从左往右、从上往下的顺序，依次在输入数组上滑动。当卷积窗口滑动到某一位置时，窗口中的输入子数组与核数组按元素相乘并求和，得到输出数组中相应位置的元素。输出数组高和宽分别为2，其中的4个元素由二维互相关运算得出：

0×0+1×1+3×2+4×3=19

1×0+2×1+4×2+5×3=25

3×0+4×1+6×2+7×3=37

4×0+5×1+7×2+8×3=43

下面我们将上述过程实现在corr2d函数里。它接受输入数组X与核数组K，并输出数组Y。使用mxnet实现:

from mxnet import autograd, nd
from mxnet.gluon import nn

def corr2d(X, K):  # 本函数已保存在d2lzh包中方便以后使用
    h, w = K.shape
    Y = nd.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

我们可以构造图中的输入数组X、核数组K来验证二维互相关运算的输出：

X = nd.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
K = nd.array([[0, 1], [2, 3]])
corr2d(X, K)

output: 

[[19. 25.]
 [37. 43.]]
<NDArray 2x2 @cpu(0)>

2.二维卷积层

二维卷积层将输入和卷积核做互相关运算，并加上一个标量偏差来得到输出。卷积层的模型参数包括了卷积核和标量偏差。在训练模型的时候，通常我们先对卷积核随机初始化，然后不断迭代卷积核和偏差。

下面基于corr2d函数来实现一个自定义的二维卷积层。在构造函数__init__里我们声明weight和bias这两个模型参数。前向计算函数forward则是直接调用corr2d函数再加上偏差。

class Conv2D(nn.Block):
    def __init__(self, kernel_size, **kwargs):
        super(Conv2D, self).__init__(**kwargs)
        self.weight = self.params.get('weight', shape=kernel_size)
        self.bias = self.params.get('bias', shape=(1,))

    def forward(self, x):
        return corr2d(x, self.weight.data()) + self.bias.data()

卷积窗口形状为p×qp×q的卷积层称为p×qp×q卷积层。同样，p×qp×q卷积或p×qp×q卷积核说明卷积核的高和宽分别为pp和qq。