知识点汇总-数据结构(进阶版)
- 哈希函数(散列函数):类似于函数调用一样,给一个字符串作为输入,返回一个哈希码
- 哈希表(散列表):把哈希码映射到表中的一个位置来访问记录,存放记录的数组就叫散列表
- 直接寻址法:hash(key) = a * key + b
- 输入域是无穷大的,输出域是有穷的,输出域要比输入域小
- 哈希函数不是一个随机函数,只要输入一样,输出就一样
- 哈希碰撞:输入不一样也有可能得到输出一样的值
- 虽然有哈希碰撞,如果输入够多,将在整个输出域上均匀地出现返回值,不一定完全平分,但输出域中的每个哈希码一定被差不多个输入域中的值对
- 当输入域足够大,经过一个哈希函数计算完后保证输出域是均匀分布时,对输出域的每一个哈希码模%上一个m,最终的域会缩减成0至m-1,也均匀分布
- 解决哈希冲突(key1和key2称为同义词)的方法:开放寻址法,链地址法

- 布隆过滤器:布隆过滤器是一个bit类型的map,主要用于解决爬虫去重问题以及黑名单问题,其短板是它有失误率
- 一致性哈希结构:把原来全部数据迁移的代价变得很低,并负载均衡
- 并查集:(1)非常快地检查两个元素各自所在的集合是否属于一个集合(2)两个元素各自所在的集合,合并在一块
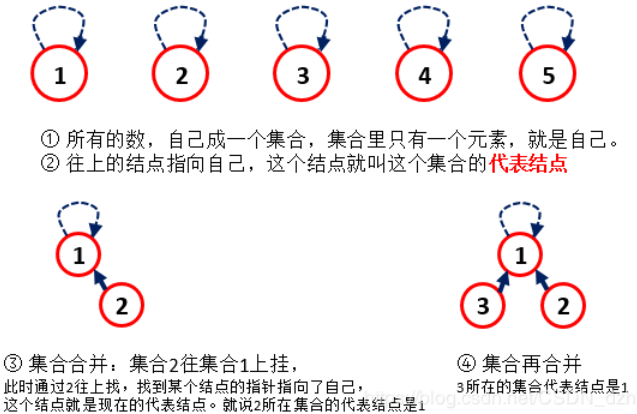
- 看出每一次查询操作的时间复杂度为O(H),H为树的高度,于是可以用下面的扁平化优化

-
前缀树(trie树):特点是效率很高(1)每个节点保存一个字符(2)根节点不保存字符(3)每个节点最多有n个子节点(n是所有可能出现字符的个数)(4)查询的复杂度为O(k),k为查询字符串长度

-
B树和B+树:解决磁盘IO问题。在大量数据存储中,查询时不能一下将所有数据加载到内存中,只能逐一加载磁盘页,每个磁盘页对应树的结点。造成大量磁盘IO操作(最坏情况下为树的高度)。于是将树变得矮胖来减少磁盘IO的次数——采用多叉树,每个结点存储多个元素,又根据AVL得到一棵平衡多路查找树可以使得数据查找效率在O(logN)
- B树:(1)每个节点都存储key和value,所有的节点组成这棵树,并且叶子结点指针为null(2)一个m阶B树最多有m个孩子,若根结点不是叶子结点,则至少有 2 个孩子(3)所有叶子结点都在一层
- B+树非叶子节点只存储key,只有叶子结点存储value,叶子结点包含了这棵树的所有键值,每个叶子结点有一个指向相邻叶子结点的指针,这样可以降低B树的高度
- B+树是数据库实现索引的首选数据结构呢?——评价一个数据结构作为索引的指标就是在查找时IO操作的次数
- B+树相比于B树的优势:(1)B+树单一节点存储更多的元素,使得查询的IO次数更少(2)B+树所有查询都要查找到叶子节点,查询效率更加稳定(3)B+树所有叶子节点形成有序链表,便于范围查询,更有利于对数据库的扫描
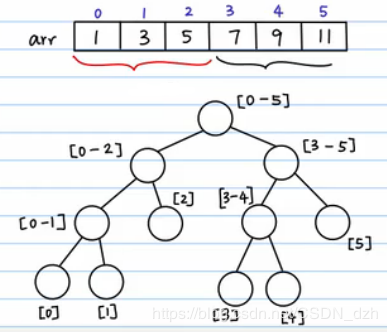
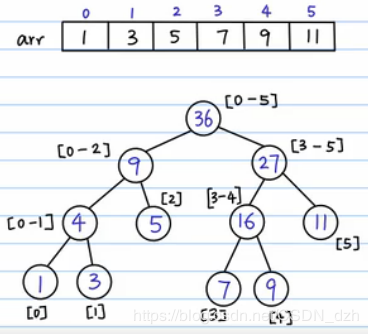
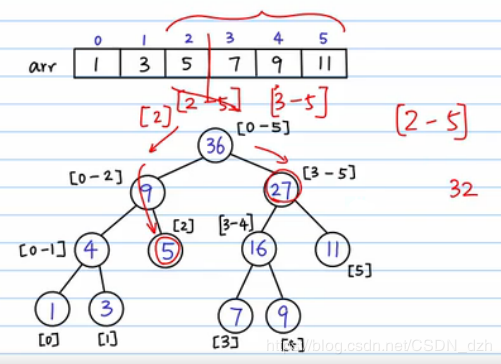
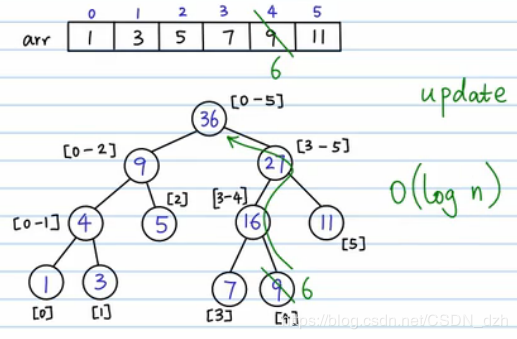
- 线段树的建立:(1)根结点表示数组元素的总和(2)分叉,把数组劈成两半。做法就是不断二分,最终所有的叶子结点就是数组中的元素(3)填每一个结点(4)有一个 query 需求,要算区间 [2, 5] 以内的和。那么我们就把这个区间分半,分成 [2] 和 [3, 5]。这样,对query,最坏情况就是把这棵树从根结点到叶子结点搜索一遍,复杂度变为了 O(logn)。(5)有另一个需求 update,要把 4 位置上的数字改为 6,那么我们就先顺着这条路找到 4 位置,然后再返回去修改这条路上的和,其他路径不会受到影响。所以总的时间复杂度也是 O(logn) 的