BUAA_OO_第一单元作业总结

简述

本单元一共分为三次作业，通过对表达式结构进行建模，完成单变量多项式的括号展开。三次作业层层递进，从单层括号到嵌套括号，在经过了开始几次的煎熬后，也让笔者初步体会到了层次化设计的思想。本篇主要围绕笔者对三次作业的构造设计进行分析总结。

第一次作业

设计思路

本次作业作为我在面向对象设计与构造课程的第一站，本次作业将题目进行了简化，在本次作业给出的表达式中，其只存在三个因子：变量因子、常数因子和表达式因子，并且无嵌套括号存在。

由于每一个表达式是由若干个项组成，而每一个项则是由若干个因子构成的，因此，笔者想到了将题目给出的表达式分割成若干个项，再对于每一个项，利用正则匹配的方法，将表达式因子提取出来，进行单独分析，然后又考虑到项中因子只存在相乘的关系，再将表达式因子与原来的项进行相乘，从而将括号消去。

结构分析

Expression类

该类的结构如图：

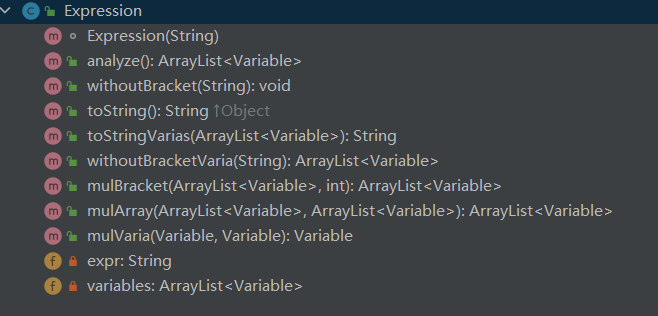
该类作为本次项目设计的关键类，其作用主要有：
- 通过analyze方法，对表达式进行分析，并将分析出的项储存到variables属性中
- 对于含有括号的项，通过递归下降的方法，去除括号后再次通过Expression类的analyze方法进行分析
- 将两个含有若干个项的容器进行相乘运算，并返回结果
Term类

该类结构如图：

该类主要用于对多个项进行合并同类项，并返回字符串结果
Variable类

该类结构如图：

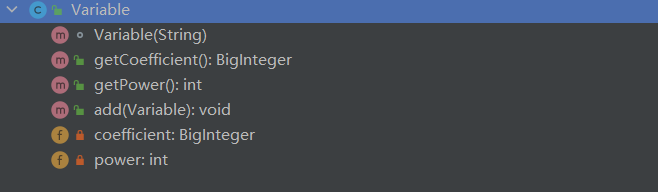
考虑到本次题目对于变量的限制，因此笔者将每个因子抽象成了 [系数]*x**[幂] 的形式，从而对于每一项来说，只需要考虑其因子的系数和幂
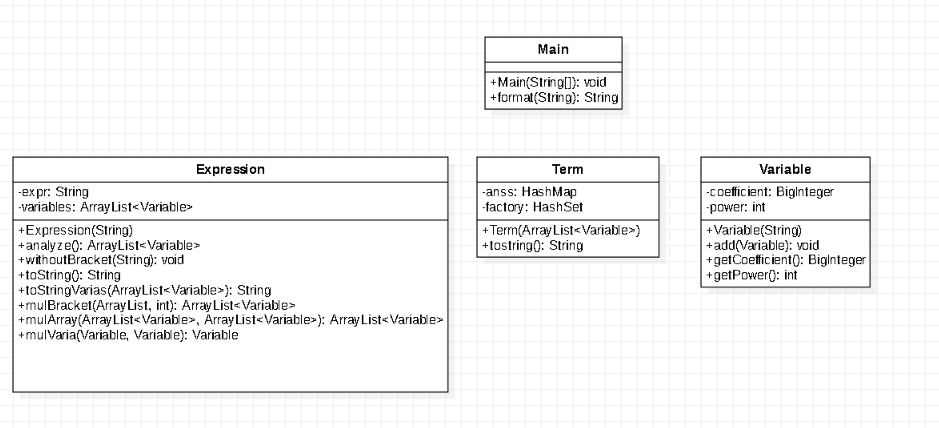
总UML图

度量分析

方法复杂度分析

method	CogC	ev(G)	iv(G)	v(G)
Variable.Variable(String)	9.0	1.0	5.0	5.0
Variable.getPower()	0.0	1.0	1.0	1.0
Variable.getCoefficient()	0.0	1.0	1.0	1.0
Variable.add(Variable)	0.0	1.0	1.0	1.0
Term.toString()	73.0	3.0	14.0	17.0
Term.Term(ArrayList)	4.0	1.0	3.0	3.0
Main.main(String[])	0.0	1.0	1.0	1.0
Main.format(String)	6.0	1.0	6.0	6.0
Expression.withoutBracketVaria(String)	3.0	1.0	3.0	3.0
Expression.withoutBracket(String)	3.0	1.0	3.0	3.0
Expression.toStringVarias(ArrayList)	1.0	1.0	2.0	2.0
Expression.toString()	19.0	2.0	7.0	7.0
Expression.mulVaria(Variable, Variable)	0.0	1.0	1.0	1.0
Expression.mulBracket(ArrayList, int)	4.0	3.0	3.0	3.0
Expression.mulArray(ArrayList, ArrayList)	3.0	1.0	3.0	3.0
Expression.Expression(String)	0.0	1.0	1.0	1.0
Expression.analyze()	18.0	2.0	9.0	10.0
Total	143.0	23.0	64.0	68.0
Average	8.411764705882353	1.3529411764705883	3.764705882352941	4.0

类复杂度分析

class OCavg OCmax WMX

Expression 3.2222222222222223 7.0 29.0

Main 3.5 6.0 7.0

Term 9.5 16.0 19.0

Variable 2.0 5.0 8.0

Total 63.0

Average 3.7058823529411766 8.5 15.75

class	OCavg	OCmax	WMX
Expression	3.2222222222222223	7.0	29.0
Main	3.5	6.0	7.0
Term	9.5	16.0	19.0
Variable	2.0	5.0	8.0
Total			63.0
Average	3.7058823529411766	8.5	15.75

BUG分析

在本次的作业中，笔者主要使用了正则匹配来对表达式进行分割查找，但是，在使用正则匹配来对复杂字符串进行查找时，使用的正则匹配表达式也更加复杂，因此往往会出现一些意想不到的bug，也正是因为这个原因，笔者在互测时出现了bug。

在对字符串进行分析的工作中，正则匹配毫无疑问是一个非常优秀的工具，但是，在我们对比较复杂的字符串进行分析查找时，也要注意正则匹配表达式过长而导致的某些潜在的问题，而这些问题往往是比较难发现的。

第二次作业

设计思路

相较于上一次作业，本次作业主要增加了三角函数、自定义函数以及嵌套括号的要求，由于笔者在上一次的作业中主要采用的正则匹配的方法来对字符串进行分割解析，而在本次作业中，因为三角函数的增加，使得构造正则表达式的难度大大增加，并且考虑到使用正则表达式时会出现的bug问题，因此笔者选择了重构。

在本次作业中，核心思想还是和上次作业一样，将自定义函数带入表达式后，将新得到的表达式按照项进行分割，再对每一项进行判断，若不存在括号，则将其交给Term类进行解析，若存在括号，则将其去除括号后交给Expression类进行递归解析，然后再与剩下的因子相乘，最终实现对括号的去除。

结构分析

Function类

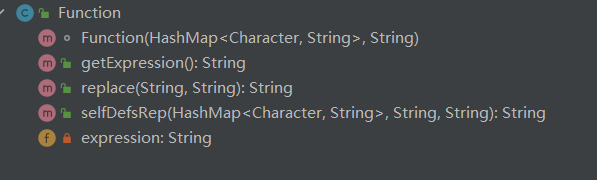
该类的作用主要是处理自定义函数（含有f、g、h）和sum求和函数。在处理自定义函数时，笔者主要通过HashMap来建立参数对应的关系，并进一步将表达式字符串中的自定义函数替换。

Expression类

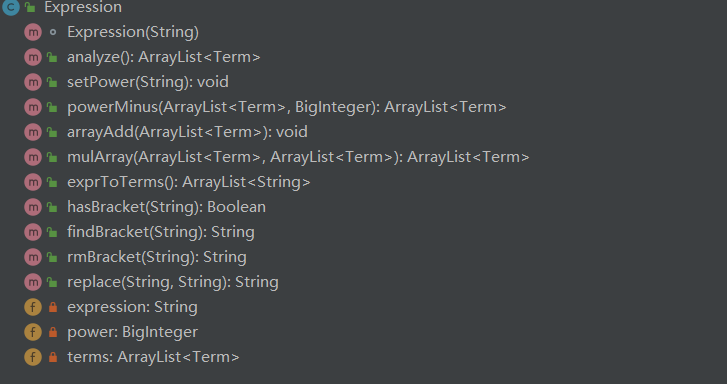
考虑到表达式字符串的复杂性，笔者在该类中对于按项分割等方法进行了重写如：

exprToTerms()：将表达式字符串按项分割成若干项。
findBracket()：找出项中括号存在的部分。
replace()：将项中括号部分替换成1。

该类的核心思想是，将表达式按项分割，对于每一项，若存在括号，则将括号部分去除括号后放入新的Expression类进行解析，剩下部分将括号部分替换成1后放入另一个Expression类解析，然后将两个Expression类解析后的结果相乘后，放入该类的terms属性中。将每一项解析完成以后，最后返回expression表达式指数运算后的结果（power属性默认为1）。

Term类

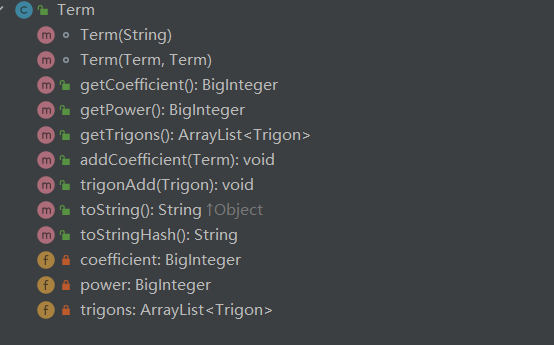
在本项目中，笔者将项类抽象成了 [系数]*x**[幂]*[三角函数类]···的形式，因此该类储存了系数-coeffcient，幂-power，三角函数容器-trigons，便于我们对项进行加减乘操作。

Trigon类

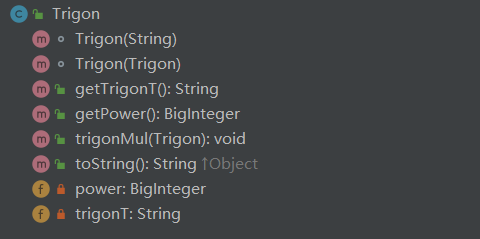
该类主要储存了三角函数的比较关键的两个部分，本体-用String储存和幂-用BigInteger储存。

总UML图

度量分析

方法复杂度分析

method	CogC	ev(G)	iv(G)	v(G)
Trigon.trigonMul(Trigon)	0.0	1.0	1.0	1.0
Trigon.Trigon(Trigon)	0.0	1.0	1.0	1.0
Trigon.Trigon(String)	2.0	1.0	2.0	2.0
Trigon.toString()	0.0	1.0	1.0	1.0
Trigon.getTrigonT()	0.0	1.0	1.0	1.0
Trigon.getPower()	0.0	1.0	1.0	1.0
Term.trigonAdd(Trigon)	5.0	3.0	3.0	4.0
Term.toStringHash()	1.0	1.0	2.0	2.0
Term.toString()	1.0	1.0	2.0	2.0
Term.Term(Term, Term)	2.0	1.0	3.0	3.0
Term.Term(String)	9.0	1.0	6.0	6.0
Term.getTrigons()	0.0	1.0	1.0	1.0
Term.getPower()	0.0	1.0	1.0	1.0
Term.getCoefficient()	0.0	1.0	1.0	1.0
Term.addCoefficient(Term)	0.0	1.0	1.0	1.0
Main.print(HashMap)	30.0	1.0	10.0	11.0
Main.mergeSim(ArrayList)	4.0	1.0	3.0	3.0
Main.main(String[])	1.0	1.0	2.0	2.0
Main.format(String)	6.0	1.0	6.0	6.0
Function.selfDefsRep(HashMap, String, String)	40.0	1.0	12.0	14.0
Function.replace(String, String)	0.0	1.0	1.0	1.0
Function.getExpression()	0.0	1.0	1.0	1.0
Function.Function(HashMap, String)	15.0	1.0	5.0	7.0
Expression.setPower(String)	1.0	1.0	2.0	2.0
Expression.rmBracket(String)	0.0	1.0	1.0	1.0
Expression.replace(String, String)	5.0	3.0	4.0	5.0
Expression.powerMinus(ArrayList, BigInteger)	4.0	3.0	3.0	3.0
Expression.mulArray(ArrayList, ArrayList)	3.0	1.0	3.0	3.0
Expression.hasBracket(String)	0.0	1.0	1.0	1.0
Expression.findBracket(String)	38.0	1.0	9.0	19.0
Expression.exprToTerms()	13.0	1.0	6.0	9.0
Expression.Expression(String)	0.0	1.0	1.0	1.0
Expression.arrayAdd(ArrayList)	0.0	1.0	1.0	1.0
Expression.analyze()	4.0	1.0	3.0	3.0
Total	184.0	40.0	101.0	121.0
Average	5.411764705882353	1.1764705882352942	2.9705882352941178	3.5588235294117645

类复杂度分析

class	OCavg	OCmax	WMX
Expression	3.727272727272727	13.0	41.0
Function	5.0	11.0	20.0
Main	5.5	11.0	22.0
Term	2.3333333333333335	6.0	21.0
Trigon	1.1666666666666667	2.0	7.0
Total			111.0
Average	3.264705882352941	8.6	22.2

本次作业的复杂度相较于上一次错作业，出现了明显的上升，其主要还是由于嵌套括号的多次迭代，使得系统复杂度提升。

BUG分析

在这次作业中，笔者出现了较多的bug，但是经过笔者的检查，发现主要bug是来源于Function类对于自定义函数的处理，由于在对自定义函数处理时缺少了一些必要的括号，导致后续处理的结果发生了错误。总的来说，还是笔者对于本次的测试还不够完善。

第三次作业

设计思路

本次作业相较于上一次作业来说，改变不是很大，主要是支持自定义函数的嵌套和三角函数的因子包括了表达式因子，因此，笔者在Trigon类中引入了Expression类对三角函数括号中的因子进行分析。

结构分析

本次作业相较于上一次作业，主要改动了Function类和Trigon类，因而笔者在此只展示这两个类的结构。

Function类
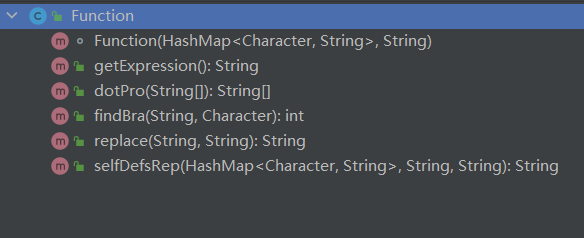
Trigon类

度量分析

方法复杂度分析

method	CogC	ev(G)	iv(G)	v(G)
Trigon.trigonMul(Trigon)	0.0	1.0	1.0	1.0
Trigon.Trigon(Trigon)	0.0	1.0	1.0	1.0
Trigon.Trigon(String)	2.0	1.0	2.0	2.0
Trigon.toString()	0.0	1.0	1.0	1.0
Trigon.print(HashMap)	30.0	3.0	10.0	11.0
Trigon.mergeSim(ArrayList)	4.0	1.0	3.0	3.0
Trigon.getTrigonT()	0.0	1.0	1.0	1.0
Trigon.getPower()	0.0	1.0	1.0	1.0
Trigon.formPrint(String)	0.0	1.0	1.0	1.0
Trigon.findTrigon(String)	17.0	1.0	5.0	13.0
Term.trigonAdd(Trigon)	5.0	3.0	3.0	4.0
Term.toStringHash()	1.0	1.0	2.0	2.0
Term.toString()	1.0	1.0	2.0	2.0
Term.Term(Term, Term)	2.0	1.0	3.0	3.0
Term.Term(String)	10.0	1.0	7.0	7.0
Term.isTrigon(String)	1.0	1.0	2.0	2.0
Term.getTrigons()	0.0	1.0	1.0	1.0
Term.getPower()	0.0	1.0	1.0	1.0
Term.getCoefficient()	0.0	1.0	1.0	1.0
Term.findTrigon(String, int)	32.0	3.0	13.0	23.0
Term.addCoefficient(Term)	0.0	1.0	1.0	1.0
Main.print(HashMap)	31.0	1.0	11.0	12.0
Main.mergeSim(ArrayList)	4.0	1.0	3.0	3.0
Main.main(String[])	1.0	1.0	2.0	2.0
Main.format(String)	7.0	1.0	7.0	7.0
Function.selfDefsRep(HashMap, String, String)	26.0	1.0	9.0	11.0
Function.replace(String, String)	0.0	1.0	1.0	1.0
Function.getExpression()	0.0	1.0	1.0	1.0
Function.Function(HashMap, String)	15.0	1.0	5.0	7.0
Function.findBra(String, Character)	3.0	1.0	2.0	3.0
Function.dotPro(String[])	5.0	1.0	2.0	4.0
Expression.setPower(String)	1.0	1.0	2.0	2.0
Expression.rmBracket(String)	0.0	1.0	1.0	1.0
Expression.replace(String, String)	5.0	3.0	4.0	5.0
Expression.powerMinus(ArrayList, BigInteger)	4.0	3.0	3.0	3.0
Expression.mulArray(ArrayList, ArrayList)	3.0	1.0	3.0	3.0
Expression.hasBracket(String)	19.0	1.0	3.0	9.0
Expression.findBracket(String)	38.0	1.0	9.0	20.0
Expression.exprToTerms()	13.0	1.0	6.0	9.0
Expression.Expression(String)	0.0	1.0	1.0	1.0
Expression.arrayAdd(ArrayList)	0.0	1.0	1.0	1.0
Expression.analyze()	4.0	1.0	3.0	3.0
Total	284.0	52.0	141.0	190.0
Average	6.761904761904762	1.2380952380952381	3.357142857142857	4.523809523809524

类复杂度分析

class	OCavg	OCmax	WMX
Expression	4.454545454545454	14.0	49.0
Function	4.166666666666667	9.0	25.0
Main	6.0	12.0	24.0
Term	3.1818181818181817	12.0	35.0
Trigon	2.9	11.0	29.0
Total			162.0
Average	3.857142857142857	11.6	32.4

BUG分析

本次作业的bug主要来源于本项目代码不支持直接对常数的幂进行计算，后期化简时的考虑不仔细，以及sum求和函数对于参数e和t的范围没有仔细考虑。

第一单元总结与感想

本单元是笔者在面向对象设计与构造课程的第一站，由于笔者刚刚接触基于面向对象的设计思想，因此在本次作业的设计构造过程中还存在着很多不如意的地方，比如在这几次的作业中，类与类之间的耦合性偏高以及内聚性明显不足，类的抽象程度也还明显不够，这也就导致了我的几个类中方法以及代码规模比较大。

当然，在这几次的作业过程中我也对面向过程的设计方法有了一定的了解和熟悉。当我们去解决一个问题时，面向对象的设计，就是将问题中的事物抽象成一个个的对象，然后赋予一定的属性和方法，然后让每个对象去执行自己的方法，从而解决问题。这种让对象自己去解决问题的方法，既保证了数据的安全稳定，又易于维护，使得系统更具有灵活性。而一个好的面向对象的设计，他的对象一般是高度抽象的，更利于凸显事物的本质属性。

同时，在项目的开发过程中，和其他人一起讨论并分享自己的思路，我认为是一个非常重要的过程。在和他人的讨论过程中，我们往往会收获到一些十分有用的方法，比如，在合并同类项时，我们可以考虑利用HashMap，将系数作为value，去除系数剩下的部分作为对应的key。采用这种方法，可以比较高效的查找相同项并进行合并。

最后，希望我能在接下来的学习中，能够不断强化自己面向对象的思维，加强自己作业的层次化设计，增强自己的架构设计能力。

posted @ 2022-03-25 23:30 Zhenlee 阅读(29) 评论(0) 编辑收藏举报

刷新页面返回顶部

zhenlee-blog

BUAA_OO_第一单元作业总结

简述

第一次作业

设计思路

结构分析

Expression类

Term类

Variable类

总UML图

度量分析

方法复杂度分析

类复杂度分析

BUG分析

第二次作业

设计思路

结构分析

Function类

Expression类

Term类

Trigon类

总UML图

度量分析

方法复杂度分析

类复杂度分析

BUG分析

第三次作业

设计思路

结构分析

Function类

Trigon类

度量分析

方法复杂度分析

类复杂度分析

BUG分析

第一单元总结与感想

公告