时间序列分析中预测类问题下的建模方案

【说在前面】本人博客新手一枚，象牙塔的老白，职业场的小白。以下内容仅为个人见解，欢迎批评指正，不喜勿喷！[认真看图][认真看图]

【补充说明】时间序列分析主要有两个方向，一个通过是对历史数据的分析进行异常检测和分类，二是进行预测！ 

【补充说明】回归分析假设每个数据点都是独立的，而时间序列分析则是利用数据之间的相关性进行预测！

【多说一句】本文主要对时间序列分析中预测类问题下的建模方案进行探讨，其他内容之后再分享！

一、基于统计学模型

1. 基本概念

一个时间序列可能存在的特征包括以下几种：

• 趋势：时间序列在长时间内呈现出来的长期上升或下降的变动
• 季节性：时间序列在一年内出现的周期性波动，例如销售淡季和销售旺季等
• 序列相关性：又称为自相关性。即时间序列中数据点之间存在正相关或者负相关
• 随机噪声：时间序列中除去趋势、季节变化和自相关性之后的剩余随机扰动。

时间序列中预测类问题的目标是利用统计建模来识别时间序列中潜在的趋势、季节变化和序列相关性。

而衡量一个模型是否适合原始时间序列的标准正是考察原始值和拟合值之间的残差序列是否近似的为白噪声。

因此，首先要进行时间序列的自相关性分析，确定训练数据是符合时间序列要求：

• 用时滞图观察：时滞图是把时间序列的值及相同序列在时间轴上后延的值放在一起展示。
• Ljung-Box检验：是一种对平稳性检验的方法，判断一个序列是白噪声还是序列存在相关性。

时间序列建模的过程可以总结如下：

2. 平稳性检验

如果想要对时间序列进行统计学模型分析，需要保证时间序列具有平稳性。

在数学上，时间序列的严平稳有着更精确的定义：它要求时间序列中任意给定长度的两段子序列都满足相同的联合分布。这是一个很强的条件，在实际中几乎不可能被满足。因此还有弱平稳的定义，它要求时间序列满足均值平稳性和二阶平稳性（方差平稳性）。

检验平稳性的方法有很多种：

（1）图示法

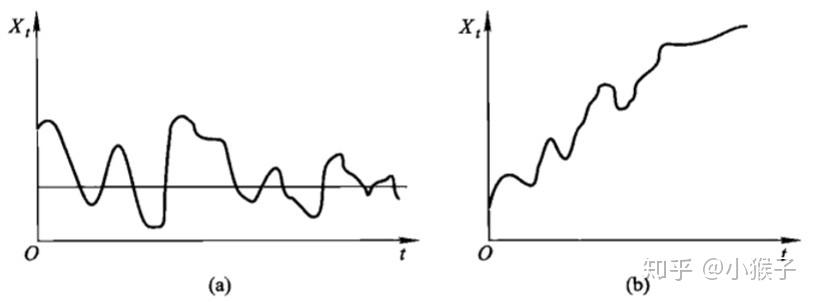
根据时序图粗略判断是否平稳：平稳时序图的特征为围绕均值波动，而非平稳时序图表现为在不同时间段具有不同的均值。

即可以从两个特征进行判断：趋势（即均值随时间变化）、季节性（即方差随时间变化、自协方差随时间变化）。

如图所示，图a为平稳时序图，图b为非平稳时序图。

（2）单位根检测法

例如DF检验、ADF检验、KPSS、P-P等，具体不展开介绍。

3. 平稳化处理

• 变换：例如取对数、取平方等
• 平滑处理：例如移动平均等
• 差分
• 分解
• 多项式拟合：例如拟合回归等

4. 统计学模型：自回归模型 AR

数学上，满足如下关系的时间序列 被称为一个 阶的自回归模型，记为 模型：

阶的意思是使用当前时刻 之前的 个观测值作为自变量对 建模。模型的含义是， 可以表达为 时刻之前的 个收益率观测值的线性组合以及一个 时刻的随机误差 。 的取值可以是任何一个正整数，因此最简单的自回归模型就是 模型（ ）。

需要说明的是，自回归模型不一定都满足平稳性。

5. 统计学模型：滑动平均模型 MA

数学上，满足如下关系的时间序列 被称为一个 阶的滑动平均模型，记为 模型：

与自回归模型不同，滑动平均模型一定满足平稳性。

6. 统计学模型：自回归滑动平均模型 ARMA

ARMA模型是针对平稳时间序列建立的模型。将一个 阶的自回归模型和一个 阶的滑动平均模型组合在一起，将 AR 和 MA 模型的优势互补起来。由于 AR 和 MA 模型都是线性模型，因此它俩的线性组合，即 ARMA 模型，也是线性模型。

数学上，满足如下关系的时间序列 被称为一个阶数为 的自回归滑动平均模型，记为 模型：

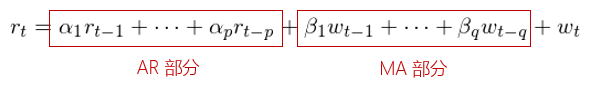
相比较单一的 AR 或者 MA 模型，ARMA 模型拥有更多的参数，出现过拟合的危险就更高。因此，在确定 AR、MA 以及 ARMA 模型的阶数时，常使用信息量准则，包括赤池信息量准则（简称 AIC）以及贝叶斯信息量准则（简称 BIC）。这两个信息量准则的目的都是寻找可以最好地解释数据但包含最少自由参数的模型，均使用模型的似然函数、参数个数以及观测点个数来构建一个标量函数，以此作为评价模型好坏的标准，区别在于标量函数的表达式有所不同。

7. 统计学模型：差分整合移动平均自回归模型 ARIMA

ARIMA （p，d，q）模型是针对非平稳时间序列建模，在ARMA模型的基础上多了差分项（即前文提到的平稳化处理）。其中AR是“自回归”，p为自回归项数，MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数。其中，对于p，d，q的选择是通过ACF（自相关函数，描述了时间序列数据与其之后版本的相关性）与PACF（偏自相关函数，描述了各个序列的相关性）来确定的。

8. 统计学模型：季节性差分自回归滑动平均模型 SARIMA

在 ARIMA 模型的基础上进行了季节性调节。不同的是SARIMA的差分项有两个，分别是季节性差分与非季节性差分。

9. 模型检验：残差检验

如果一个模型和原时间序列的残差满足白噪声，那么该模型就是合适的。因此，只需要检验残差序列是否在任何间隔 k 上呈现出统计意义上显著的自相关性。在这方面，Ljung–Box 检验是一个很好的方法，它同时检验残差序列各间隔的自相关系数是否显著的不为 0。

最后，分享大佬总结的一些内容：时间序列分析常用统计模型

• 单变量时间序列统计学模型：例如平均方法、平滑方法、有/无季节性条件的 ARIMA 模型等
• 多变量时间序列统计学模型：例如外生回归变量、VAR等
• 附加或组件模型：例如Facebook Prophet、ETS等
• 结构化时间序列模型：例如贝叶斯结构化时间序列模型、分层时间序列模型等

二、基于机器学习模型

时间序列预测类问题被抽象为回归问题，从而可以使用机器学习的相关模型，不需要受到基本假设的限制，适用范围更广。

具体方法包括但不限于线性回归、支持向量机、随机森林、xgboost等。

关于机器学习/数据挖掘的全流程介绍，欢迎浏览我的另一篇博客：数据挖掘比赛/项目全流程介绍，这里不再赘述。

值得一提的是，机器学习在特征工程阶段，可以提取时间截面特征/统计特征/滑窗特征等，也可以借助特征提取工具（例如tsfresh等）。

三、基于深度学习模型

具体方法包括但不限于卷积神经网络CNN、循环神经网络LSTM等，目前还有用生成对抗网络GAN等比较新的技术来实现时间序列预测。

关于循环神经网络，欢迎浏览我的另一篇博客：深度学习中的序列模型演变及学习笔记，这里不再赘述。

关于深度学习模型，欢迎浏览我的另一篇博客：深度学习中的一些组件及使用技巧，这里不再赘述。

值得一提的是，深度学习在准备数据时，需要将时序数据通过时间滑窗进行时间步的拼接，从而作为训练集的输入与标签。

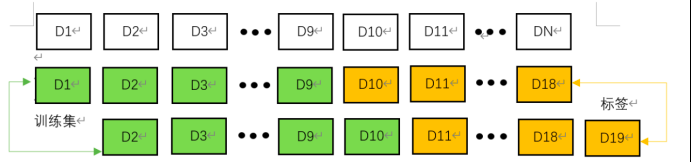
综上所述，三种类型的模型各有所长和不足。一般来说，统计类模型适合于数据量较小同时工业化需求不高的情况，机器学习类模型更广泛适合于工业化情境，而深度学习模型在大数据量的预测上更具备优势。

 

如果你对智能推荐感兴趣，欢迎浏览我的另一篇随笔：智能推荐算法演变及学习笔记

如果你对广告推荐感兴趣，欢迎浏览我的另一篇随笔：CTR预估模型演变及学习笔记

如果您对人工智能算法感兴趣，欢迎浏览我的另一篇博客：人工智能新手入门学习路线和学习资源合集（含AI综述/python/机器学习/深度学习/tensorflow）、人工智能领域常用的开源框架和库（含机器学习/深度学习/强化学习/知识图谱/图神经网络）

如果你是计算机专业的应届毕业生，欢迎浏览我的另外一篇博客：如果你是一个计算机领域的应届生，你如何准备求职面试？

如果你是计算机专业的本科生，欢迎浏览我的另外一篇博客：如果你是一个计算机领域的本科生，你可以选择学习什么？

如果你是计算机专业的研究生，欢迎浏览我的另外一篇博客：如果你是一个计算机领域的研究生，你可以选择学习什么？

如果你对金融科技感兴趣，欢迎浏览我的另一篇博客：如果你想了解金融科技，不妨先了解金融科技有哪些可能？

之后博主将持续分享各大算法的学习思路和学习笔记：hello world: 我的博客写作思路