机器学习中的聚类算法演变及学习笔记
【说在前面】本人博客新手一枚,象牙塔的老白,职业场的小白。以下内容仅为个人见解,欢迎批评指正,不喜勿喷![认真看图][认真看图]
【补充说明】聚类算法可以作为独立方法将数据聚成不同簇,也可以作为数据挖掘任务(例如分类、关联规则等)的预处理!
【补充说明】聚类算法与分类算法的主要区别在于训练时的样本有无标签,聚类算法无监督学习,分类算法有监督学习!
【再说一句】本文主要介绍机器学习中聚类算法的演变路径,和往常一样,不会详细介绍各算法的具体实现,望理解!
一、相似性衡量方法
1. 基于距离
- 闵可夫斯基距离(Minkowski Distance):计算距离的通用的公式
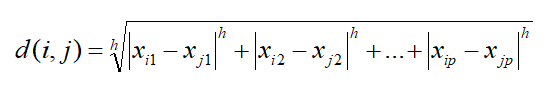
- 曼哈顿距离(即城市块距离Manhattan distance):h=1(例如用于L1正则化等)
![]()
- 欧几里德距离(用的比较多):h=2(例如用于L2正则化等)

- 其他距离:例如核函数距离K(x,y)、DTW距离、Mahalanobis距离等
2. 基于相似系数
例如余弦相似度等,主要优势在于不受原线性变换的影响,可以轻松地转换为距离,但其运算速度相对较慢。
二、基于划分的聚类
1. K-Means聚类
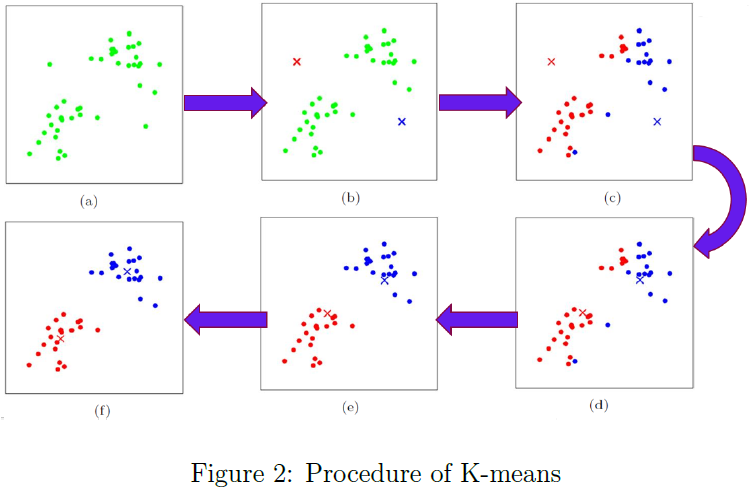
主要步骤如下:
(1)确定要聚类的数量K,并随机初始化K个簇的中心点。
(2)将每个样本分配到与其距离最近的中心点所在的簇(这里采用欧氏距离)。
(3)计算每一个簇内所有样本点的平均值,作为该簇的新中心点。
迭代重复以上这些步骤,直到各簇中心点在迭代过程中变化不大(即小于设定的阈值)。
K-Means聚类的优点:
- 原理简单,实现容易,收敛速度快
- 参数只有K,计算复杂度相对较低
- 模型可解释性强
K-Means聚类的缺点:
- 需要事先确定聚类的簇数(即K值)
- 对簇中心初始值的选取比较敏感
- 对噪声和离群点很敏感
- 采用迭代方法,容易陷入局部最优
- 适用场景有限,不能解决非凸数据
2. K值的选取
- 根据数据的可视化分布情况,结合对业务场景理解,人工选定K值
- Elbow method(即手肘法则):通过WSS随聚类数量K的变化曲线,取手肘位置的K(例如Gap Statistic、Jump Statistic等)
- 通过计算类内内聚程度和类间分离度来确定K(例如使用平均轮廓系数、类内距离/类间距离等)
- 其他:例如使用ISODATA、Gap Statistic公式、计算不同K值下的BIC/AIC、X-means clustering(AIC/BIC)等
3. K-Means聚类变体:考虑到K-Means对簇中心初始值的选取比较敏感
例如k-means++、intelligent k-means、genetic k-means、CLARANS等。这里以常见的k-means++为例,进行介绍。
k-means++按照如下的思想选取K个聚类中心:
- 在选取第一个聚类中心(n=1)时,同样是通过随机的方法。
- 在选取第n+1个聚类中心时,距离当前n个聚类中心越远的点会有更高的概率被选为第n+1个聚类中心。
4. K-Means聚类变体:考虑到k-means对噪声和离群值很敏感
例如k-medoids、k-medians等。这里以常见的k-medians为例,进行介绍。
k-medians对于中心点的选取方式是中位值。原因在于,噪声和离群点对中位值的变化影响不大。但是需要排序,速度较慢。
5. K-Means聚类变体:考虑到k-means不适用于类别型数据
例如k-modes等。这里以常见的k-modes为例,进行介绍。
k-modes算法采用差异度来代替k-means算法中的距离。k-modes算法中差异度越小,则表示距离越小。
6. K-Means聚类变体:考虑到k-means不能解决非凸数据
例如kernel k-means、谱聚类等。这里以常见的kernel k-means为例,进行介绍。
kernel k-means通过一个非线性映射,将输入空间中的数据点映射到一个高维特征空间中,使得样本在核空间线性可分,在特征空间聚类。
值得一提的是,谱聚类算法是建立在图论中的谱图理论基础上,其本质是将聚类问题转化为图的最优划分问题,是一种点对聚类算法。
三、基于密度的聚类
1. Mean-Shift聚类
均值漂移聚类是基于滑动窗口的算法,寻找数据点的密集区域。类似爬山,每一次迭代都向密度更高的区域移动,直到收敛。
主要步骤如下:
(1)确定滑动窗口半径r,以随机选取的中心点C、半径为r的圆形滑动窗口开始滑动。
(2)每一次滑动到新区域,计算窗口内的均值作为中心点,窗口内的点数量作为密度。在每一次移动中,窗口会想密度更高的区域移动。
(3)移动窗口,直到窗口内的密度不再增加为止。
其中,步骤1到3会产生很多个滑动窗口,当多个滑动窗口重叠时,保留包含最多点的窗口,然后根据数据点所在的滑动窗口进行聚类。

Mean-Shift聚类的优点:
- 不同于K-Means算法,均值漂移聚类算法不需要知道有多少簇,能够自动发现
- 基于密度的算法,相比于K-Means受均值影响较小
Mean-Shift聚类的缺点:
- 窗口半径r的选择需要仔细考虑
2. DBSCAN聚类
DBSCAN的聚类定义很简单,由密度可达关系导出的最大密度相连的样本集合,即为最终聚类的一个簇。
主要步骤如下:
(1)首先任意选择一个没有类别的核心对象作为种子,然后找到所有这个核心对象能够密度可达的样本集合,即为一个聚类簇。
(2)接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合,这样就得到另一个聚类簇。
一直运行到所有核心对象都有类别为止。
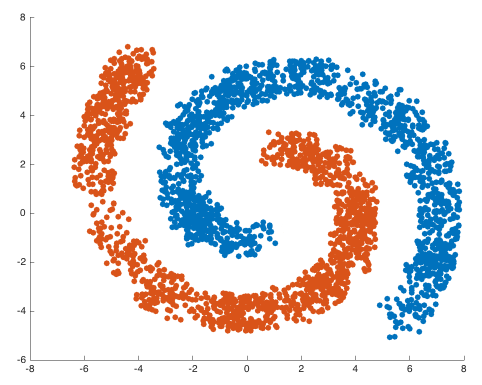
- 不需要知道有多少簇,能够自动发现
- 可以在带有噪声的空间数据库中发现任意形状的簇
DBSCAN聚类的缺点:
- 需要确定Eps领域半径、MinPts在领域中点的最少个数(即密度)这两个全局参数,较为敏感
3. DBSCAN聚类的变体
OPTICS聚类通过优先对高密度进行搜索,然后根据高密度的特点设置参数,改善了DBSCAN的不足。
当然还有其他算法,例如DENCLUE聚类等。
四、基于概率模型的聚类
1. 用高斯混合模型(GMM)的最大期望(EM)聚类
GMM聚类采用概率模型来表达原型,即通过统计得到每个样本点属于各个类的概率,而不是判定它完全属于一个类,也会被称为软聚类。
主要步骤如下:
(1)选择簇的数量,并随机初始化每个簇的高斯分布参数(即均值和方差)。
(2)给定每个簇的高斯分布,计算每个数据点属于每个簇的概率。一个点越靠近高斯分布的中心就越可能属于该簇。
(3)计算高斯分布参数,使概率最大化(EM最大期望),可用数据点概率的加权计算这些新的参数,权重就是数据点属于该簇的概率。
重复迭代步骤2和3,直到迭代中的变化不大。
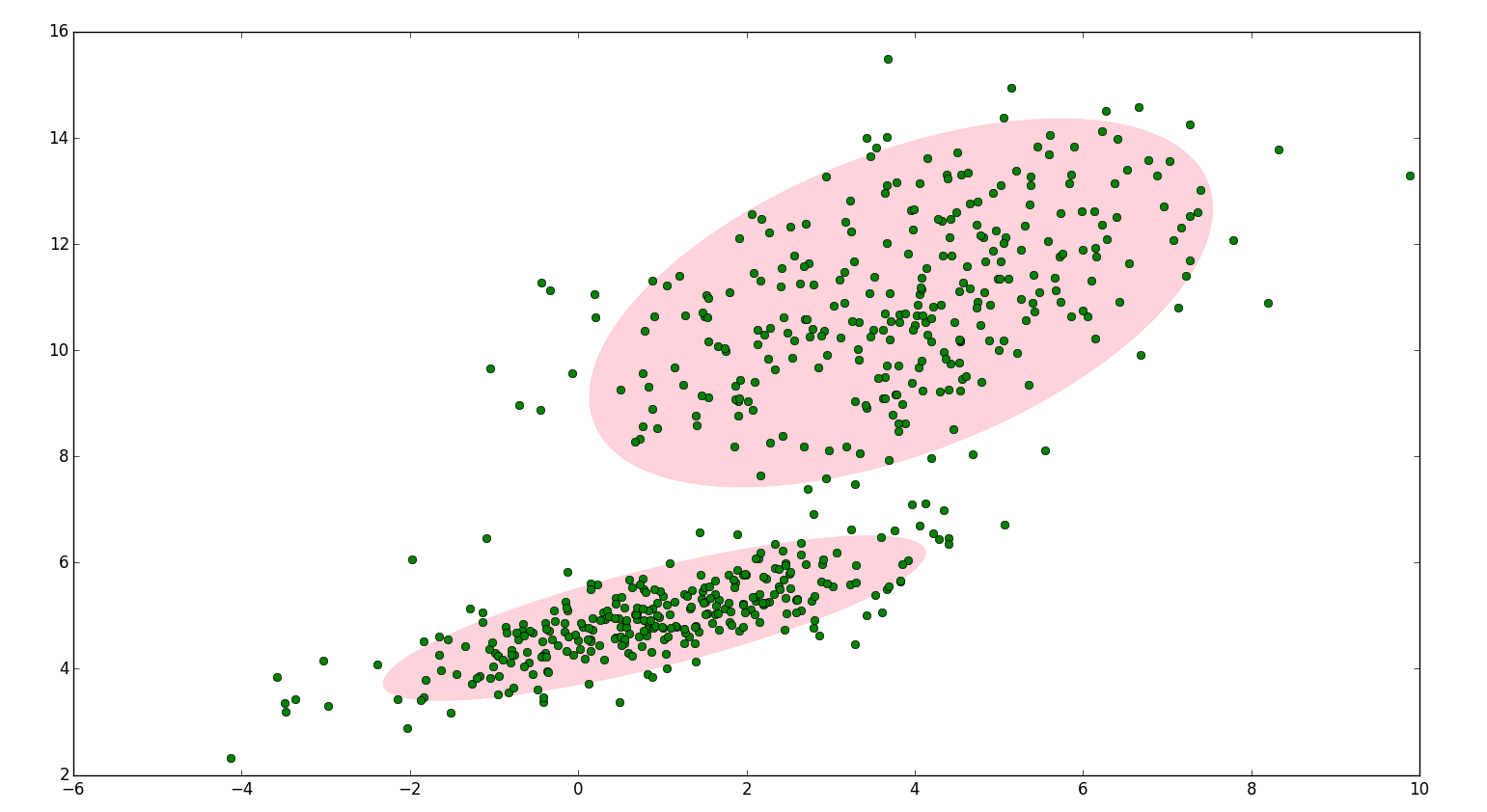
GMM聚类的优点:
- 使用均值和标准差,簇可以呈现出椭圆形,而不是仅仅限制于圆形。
- 使用概率,一个数据点可以属于多个簇。例如数据点X可以有百分之20的概率属于A簇,百分之80的概率属于B簇。
GMM聚类的缺点:
- 执行效率不高,特别是分布数量很多并且数据量很少的时候
2. 其他方法
例如基于神经网络模型的聚类SOM、基于统计学的聚类COBWeb等。
五、基于层次的聚类
对给定的数据集进行层次似的分解,直到某种条件满足为止。具体又可分为“自底向上”和“自顶向下”两种方案。
1. AGNES聚类
是一种自底向上聚合策略的层次聚类算法。
主要步骤如下:
(1)先将数据集中的每个样本看做是一个初始聚类簇。
(2)然后在算法运行的每一步中,找出距离最近的两个聚类簇进行合并。该过程不断重复,直至达到预设的聚类簇个数。
其中,如何计算簇之间的距离,并进行合并:
- 单链接算法:两个簇中距离最近的样本的距离(最小距离)
- 全链接算法:两个簇中距离最远的样本的距离(最大距离)
- 均链接算法:两个簇中每两个样本之间的距离相加求平均的距离(平均距离)
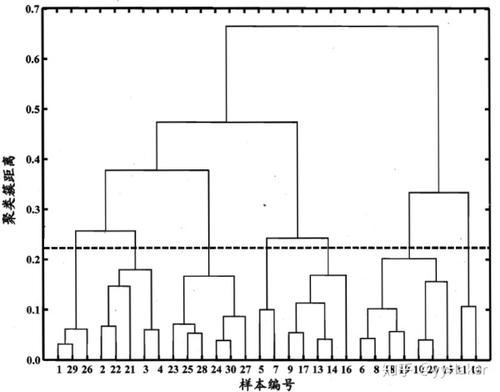
AGNES聚类的优点:
- 距离和规则的相似度容易定义,限制少
- 不需要预先制定聚类数
- 可以发现类的层次关系
- 可以聚类成其它形状
AGNES聚类的缺点:
- 计算复杂度太高
- 奇异值也能产生很大影响
- 算法很可能聚类成链状
2. BIRCH聚类
BIRCH算法是个树形结构,树的每一个节点是由若干个聚类特征CF组成。BIRCH算法比较适合于数据量大,类别数K也比较多的情况。
对于CF Tree,一般有几个重要参数:
- 第一个参数是每个内部节点的最大CF数B
- 第二个参数是每个叶子节点的最大CF数L
- 第三个参数是叶节点每个CF的最大样本半径阈值T
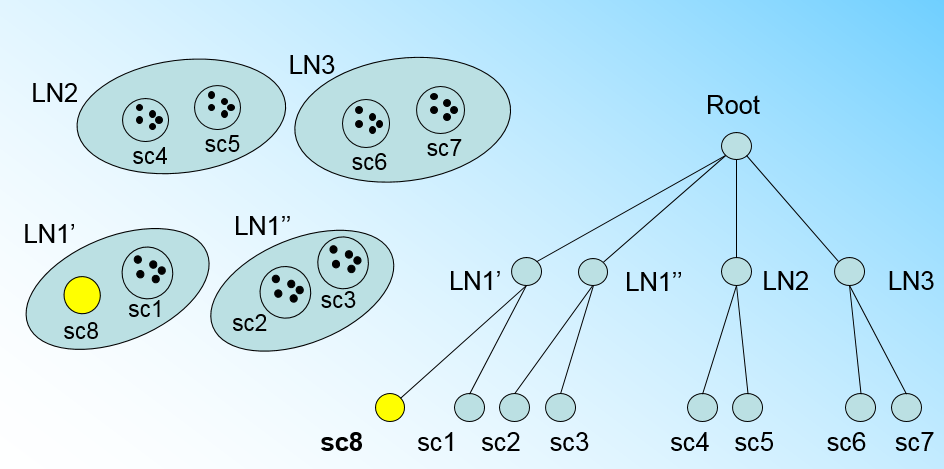
BIRCH聚类的优点:
- 不用输入聚类数K值
- 节约内存,所有的样本都在磁盘上,CF Tree仅仅存了CF节点和对应的指针
- 聚类速度快,只需要单遍扫描数据集就能建立CF Tree,CF Tree的增删改都很快
- 可以识别噪音点,还可以对数据集进行初步分类的预处理
BIRCH聚类的缺点:
- BIRCH的调参较为复杂,几个参数对CF Tree的最终形式影响很大
- 由于CF Tree对每个节点的CF个数有限制,导致聚类的结果可能和真实的类别分布不同
- 对高维特征的数据聚类效果不好(如果 n_features大于20,通常使用MiniBatchKMeans会更好)
- 如果数据集的分布簇不是类似于超球体,或者说不是凸的,则聚类效果不好
3. 其他方法
例如Diana、ROCK、CURE、CAMELEON等。
六、基于网格的聚类
核心原理就是:
(1)将数据空间划分为网格单元,将数据对象集映射到网格单元中,并计算每个单元的密度。
(2)根据预设的阈值判断每个网格单元是否为高密度单元,由邻近的稠密单元组形成”类“。
网格聚类的优点:
- 执行效率高,其速度只依赖于数据空间中每个维上单元的个数
网格聚类的缺点:
- 对参数敏感
- 无法处理不规则分布的数据
- 维数灾难
STING、CLIQUE、WaveCluster等是该类方法中的代表性算法。以下是CLIQUE的例子:

七、其他角度的聚类
例如基于约束的聚类(COD)、基于图网络的聚类(图团体检测)等。
八、聚类算法的性能度量
大佬对常用的聚类算法从可伸缩性、适合的数据类型、高维性、异常数据的抗干扰度、聚类形状和算法效率6个方面进行了综合性能评价。
还有一些对聚类的评测指标,这里不打算展开介绍了。个人感觉通过聚类来辅助具体业务场景的分析会比较重要,就像开头说的那样,聚类算法可以作为独立方法将数据聚成不同簇,也可以作为数据挖掘任务(例如分类、关联规则等)的预处理。这里要提一嘴的是,很多聚类算法都已经被封装在sklearn中,方便调用。
当然,聚类算法有很多的应用场景,例如目标用户群体分类、异常值检测等。说到这里,我接着想写一个“异常检测”专题了。

如果您对数据挖掘感兴趣,欢迎浏览我的另几篇博客:数据挖掘比赛/项目全流程介绍
如果你对智能推荐感兴趣,欢迎先浏览我的另几篇随笔:智能推荐算法演变及学习笔记
如果您对人工智能算法感兴趣,欢迎浏览我的另一篇博客:人工智能新手入门学习路线和学习资源合集(含AI综述/python/机器学习/深度学习/tensorflow)、人工智能领域常用的开源框架和库(含机器学习/深度学习/强化学习/知识图谱/图神经网络)
如果你是计算机专业的应届毕业生,欢迎浏览我的另外一篇博客:如果你是一个计算机领域的应届生,你如何准备求职面试?
如果你是计算机专业的本科生,欢迎浏览我的另外一篇博客:如果你是一个计算机领域的本科生,你可以选择学习什么?
如果你是计算机专业的研究生,欢迎浏览我的另外一篇博客:如果你是一个计算机领域的研究生,你可以选择学习什么?
如果你对金融科技感兴趣,欢迎浏览我的另一篇博客:如果你想了解金融科技,不妨先了解金融科技有哪些可能?
之后博主将持续分享各大算法的学习思路和学习笔记:hello world: 我的博客写作思路

