堆排序算法原理

更多内容，前往 IT-BLOG

它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。 

一、什么是堆

---

【1】堆是一个完全二叉树，特点是从上往下，从左往右以次排列的；
【2】在堆的数据结构中，堆中的最大值总是位于根节点，所有父节点都满足大于等于其子节点；
  ​
我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子
 ​

二、创建堆

---

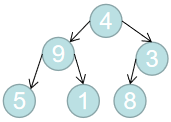
【需求】：将下面的二叉树，变成一个平衡二叉树。
  ​
【思路】：【1】先创建一个 heapfiy() 方法，从4号节点开始判断是否大于其孩子节点，如果否，则进行交换，并递归对4号节点进行 heapfiy() 操作。具体看代码操作；
【2】创建推是需要从h(树的高度)-1 层最后一个节点（3号）向上调用 heapfiy() 方法。最终就会得到堆。
【3】将上面的树转为一维数组[4,9,3,5,1,8]；
【4】父节点计算公式：parent = (i - 1) / 2；
【5】左子节点计算公式：c1 = 2i + 1；
【6】右子节点计算公式：c2 = 2i + 2；

/**
 * Created by Administrator on 2020/3/21 0021. 创建堆
 */
public class HeapSortDemo {
    /**@desc 说明1 heapfy 方法
     * @param i : 表示对那个节点进行堆的heapify
     * @param h : 表示堆的节点个数
     */
    public void heapfiy(Integer[] arr, int i, int h){
        //1、计算树的节点个数,减1代表下标
        int n = h;

        //递归需要定义一个出口
        if(i >= (n-2)/2){
            return;
        }
        //计算 i 的左子树和右子树
        int c1 = i * 2 + 1;
        int c2 = i * 2 + 2;
        int max = i;
        //判断左子树是否大于 max 下标的值
        if(c1 < n && arr[c1] > arr[max] ){
            max = c1;
        }

        //判断右子树是否大于 max 下标的值
        if(c2 < n && arr[c2] > arr[max] ){
            max = c2;
        }

        //如果 i == max 说明就是堆，否则就递归 heapfiy 调用
        if(max != i){
            swap(arr,max,i);
            heapfiy(arr,max,h);
        }
    }

    //说明2: 数组到序递归 heapify，从最后一个节点的parent;
    public void build_heap(Integer arr[],int n){
        //确定最后一个节点的父节点
        int parent = (n - 2) / 2;
        //由下向上堆排序
        for(int i = parent; i >= 0; i--){
            heapfiy(arr,i,n);
        }
    }

    //数据交换
    public void swap(Integer[] arr,int i,int n){
        int temp ;
        temp = arr[i];
        arr[i] = arr[n];
        arr[n] = temp;
    }
}

三、堆排序

---

将堆的根结点与最后一位进行交换，然后将最后一位砍断，对剩余的数组进行递归构建堆并进行首尾交换截取即可。

//堆排序
public void heapSort(Integer[] arr){
    //节点的个数
    //循环构建堆对象,i表示数组参与堆的个数
    for(int i = arr.length; i > 0; i--){
        build_heap(arr,i);
        //对第一个节点和最后一个进行交换
        swap(arr,0,i-1);
    }
}