哈夫曼树与集合

哈夫曼树的应用：根据结点不同的查找频率构造更有效的搜索树

最优二叉树/哈夫曼树：WPL（带权路径长度）最小的二叉树

typedef struct TreeNode *HuffmanTree;

struct TreeNode {

　　int Weight;

　　HuffmanTree Left, Right;

};

 

哈夫曼树的构造：每次把权值最小的两科二叉树合并

HuffmanTree Huffman ( MinHeap H ) {

　　//假设H->Size个权值已经存在H->Elements[]->Weight里

　　int i;

　　HuffmanTree T;

　　BuildMinHeap(H);　　//将H->Elements[]按权值调整为最小堆

　　for (i=1; i<H->Size; i++) {　　//做H->Size-1次合并

　　　　T = malloc ( sizeof ( struct TreeNode ) );　　//建立新结点

　　　　//从最小堆中删除一个结点，作为新T的左子结点

　　　　T->Left = DeleteMin(H);

　　　　//从最小堆中删除一个结点，作为新T的右子结点

　　　　T->Right = DeleteMin(H);

　　　　//计算新权值

　　　　T->Weight = T->Left->Weight + T->Right->Weight;

　　　　Insert( H, T );　　//将新T插入最小堆

　　}

　　T = DeleteMin (H);

　　return T;

}

选取两个最小的元素，排序方法的效率不如堆

整体复杂度为O(N logN)；

 

哈夫曼树的特点：

　　1.没有度为1的结点；

　　2.n个叶子结点的哈夫曼树共有2n-1个结点；

　　（有2个儿子的结点总数 = 叶结点总数 - 1）

　　3.哈夫曼的任意非叶结点的左右子树交换后仍是哈夫曼树；

　　4.对同一组权值，存在不同构的两棵哈夫曼树，但最优化的值WPL是一样的；

　　

前缀码：任何字符的编码都不是另一字符编码的前缀，可以无二义地编码

用二叉树进行编码：

　　1.左右分支：0，1

　　2.字符只在叶结点上

 

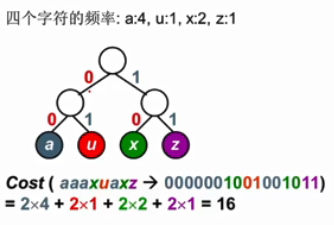
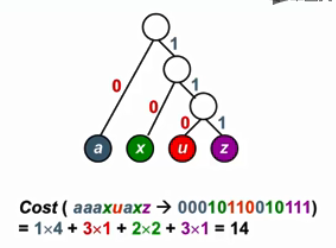
 如何构造一颗编码代价最小的二叉树——哈夫曼树

 

集合的表示

集合运算：交、并、补、差，判定一个元素是否属于某一集合

并查集：集合并、查某元素属于什么集合，可以用树结构表示集合，树的每个结点代表一个集合元素

双亲表示法：孩子指向双亲

采用数组存储形式

typedef struct {

　　ElementType Data;　　//结点的值

　　int Parent;　　//每个结点父结点的下标

} SetType;

 

（1）查找某个元素所在的集合（用根结点表示）

int Find ( SetType S[], ElementType X ) {

　　//在数组S中查找值为X的元素所属的集合

　　//MaxSize是全局变量，为数组S的最大长度

　　int i;

　　for (i=0; i<MaxSize && S[i].Data != X; i++);　　//寻找X的下标

　　if (i>=MaxSize)　　return -1;　　//未找到X,返回-1

　　for ( ; S[i].Parent >= 0; i=S[i].Parent );

　　return i;　　//找到X所属集合，返回树根结点在数组S中的下标

}

 

（2）集合的并运算

　　1.分别找到X1和X2两个元素所在集合树的根节点

　　2.如果它们不同根，则将其中一个根结点的父结点指针设置成另一个根结点的数组下标。

void Union ( SetType S[], ElementType X1, ElementType X2 ) {

　　int Root1, Root2;

　　Root1 = Find(S, X1);

　　Root2 = Find(S, X2);

　　if (Root1 != Root2)

　　　　S[Root2].Parent = Root1;

}

不断union树会越来越高，为了改善合并以后的查找性能，可以采用小的集合合并到相对大的集合中。（更改union函数）可以更改Parent的值，如果集合内有n个元素，Parent改为-n。