[NOIP2019模拟赛]LuoguP4261白金元首与克劳德斯
题目描述
给出坐标系中n个矩形,类型1的矩形每单位时间向x轴正方向移动1个单位,类型2的矩形向y轴正方向,初始矩形不重叠,一个点被矩形覆盖当且仅当它在矩形内部(不含边界),求$(-\infty ,+\infty)$时间内一个点被覆盖的最多矩形数量。n<=10^5。
分析
部分分给的可真多,$n^2$就能拿80pts(然而我n==2的特判打错了(不知道为什么我puts("0")了qwq)变成70pts)
首先:我们可以把竖着运动的矩形看成静止不动,把横着运动的矩形看成延斜率k=-1的直线运动的矩形
因为一开始没有重复矩形,所以最后最多只有两个重复,所以答案不是1,就是2
所以我们输出rand()%2+1
考试的时候把这道题当做计算几何做了...
考虑$n^2$做法:
由上面的分析可以得到,如果答案为2,只有这三种情况:
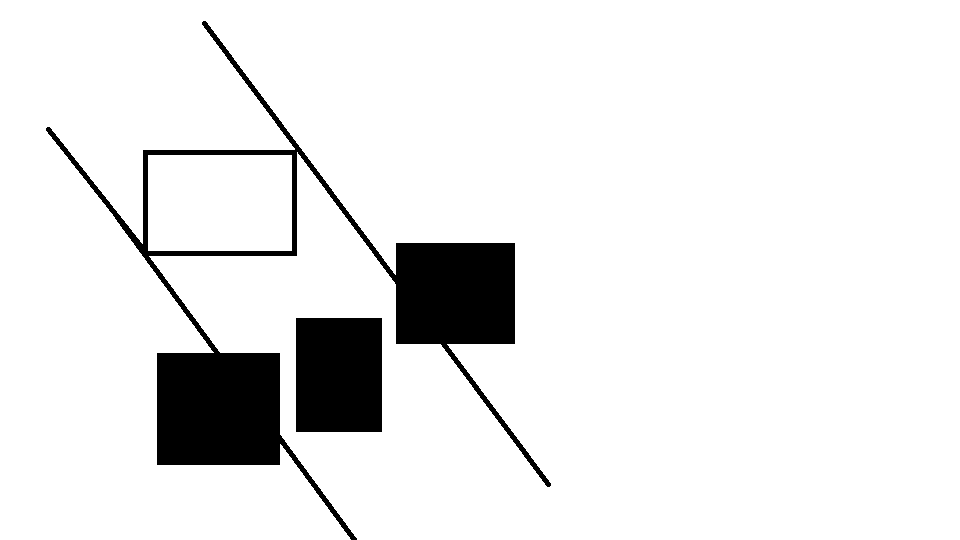
分别枚举每一个0的矩形和1的矩形判断有没有重叠就好了
注意check的时候能不能取等号
考虑优化:
显然我们可以把这题转换成区间覆盖,每个矩形变成这样的线段:
$$(x_2-x_1-w_1,x_2+w_2-x_1)$$
和
$$(y_1-y_2-h_2,y_1+h_1-y_2)$$
然后化简一下,用贪心做区间覆盖就好了(比我打的$n^2$还简单。。。)
1 #include<bits/stdc++.h> 2 using namespace std; 3 inline int read(){ 4 int ans=0,f=1;char chr=getchar(); 5 while(!isdigit(chr)){if(chr=='-')f=-1;chr=getchar();} 6 while(isdigit(chr)) {ans=(ans<<3)+(ans<<1)+chr-48;chr=getchar();} 7 return ans*f; 8 }const int M = 1e5+5; 9 int n,T,n1,n2; 10 //-----------------------------------n^2暴力做法------------------------------------ 11 struct P{int x,y,w,h;}a[M],b[M]; 12 struct Poi{int x,y;}; 13 struct Line{int a[2];}ll[M]; 14 int L[M]; 15 int s[1001][1001]; 16 inline bool check_up(Poi x,int l){ 17 int y=-x.x+l; 18 if(x.y>y) return 1; 19 return 0; 20 } 21 inline bool check_down(Poi x,int l){ 22 int y=-x.x+l; 23 if(x.y<y) return 1; 24 return 0; 25 } 26 inline bool check(Poi x,Poi y,int l1,int l2){ 27 int y1=-x.x+l1,y2=-y.x+l2; 28 if(x.y>=y1&&y.y<=y2) return 1; 29 return 0; 30 } 31 inline void Solve_1(){ 32 n=read();n1=0,n2=0; 33 for(int i=1;i<=n;i++){ 34 int x=read(),y=read(),w=read(),h=read(),d=read(); 35 if(d==0) 36 a[++n1]=(P){x,y,w,h}; 37 else b[++n2]=(P){x,y,w,h}; 38 } 39 for(int i=1;i<=n1;i++){ 40 ll[i].a[0]=a[i].x+a[i].y; 41 ll[i].a[1]=a[i].x+a[i].y+a[i].w+a[i].h; 42 }int ff=0; 43 for(int i=1;i<=n2;i++){ 44 Poi A,B; 45 A=(Poi){b[i].x,b[i].y}; 46 B=(Poi){b[i].x+b[i].w,b[i].y+b[i].h}; 47 for(int j=1;j<=n1;j++){ 48 if(check_down(A,ll[j].a[0])&&check_up(B,ll[j].a[0])|| 49 check_down(A,ll[j].a[1])&&check_up(B,ll[j].a[1])|| 50 check(A,B,ll[j].a[0],ll[j].a[1])) 51 {ff=1;break;} 52 } 53 }if(!ff) puts("1");else puts("2"); 54 } 55 //-------------------------------------------------------------------------------------------- 56 int lst[M],ff; 57 struct PP{int x,y,type;}seg[M]; 58 bool cmp(const PP&a,const PP&b){return a.x==b.x&&a.y<b.y||a.x<b.x;} 59 inline void Solve(){ 60 n=read(),ff=0; 61 for(int i=1;i<=n;i++){ 62 int x=read(),y=read(),w=read(),h=read(),d=read(); 63 seg[i]=(PP){x+y,x+y+w+h,d}; 64 }sort(seg+1,seg+n+1,cmp); 65 memset(lst,-0x3f,sizeof(lst)); 66 for(int i=1;i<=n;i++){ 67 if(seg[i].x<lst[seg[i].type^1]){ 68 puts("2"); 69 ff=1;break; 70 }lst[seg[i].type]=max(lst[seg[i].type],seg[i].y); 71 }if(!ff)puts("1"); 72 } 73 int main(){ 74 freopen("cloud.in","r",stdin); 75 freopen("cloud.out","w",stdout); 76 T=read(); 77 while(T--){ 78 // Solve_1(); 79 Solve(); 80 } 81 return 0; 82 }


