【寒假集训系列2.13】
又要爆零了...
第一题数学题,第二题打了一个错误的表,找到了错误的规律(漏加1),第三题骗分(不过只有10分)
总分:100+0+10=110
诶怎么又是110,怕是跟police过不去了...
T1集合对
题目描述:
定义集合xor操作: A xor B=A∪B-A∩B。
问有多少对(P,Q)满足 P∈A ,Q∈B 使得 (P xor A)xor(Q xor B)=A xor B其中P ,Q都是集合。(答案对1e9+7取模。)
例如:A ={1} ,B={1,2},A xor B = {2},枚举所有情况P,Q有2种。
输入:
三个整数a,b,c。表示|A|,|B|,|A∩B|。
输出:
满足要求的集合对。(输出答案对10^9+7取模)
样例输入:
1 2 1
样例输出:
2
数据规模:
50%:a,b,c<=10^6
100%: a,b,c<=10^18
思路:xor是异或的意思嘛...然后这里稍微转换一下就发现答案是:
C(N,1)+C(N,2)+C(N,3)+...+C(N,N) = 2^N (N=|A∩B|))
然后显然要快速幂啊...打上就好了...(把int #define成 long long了)
#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> #define int long long #define ll long long const int MOD=1e9+7; using namespace std; inline int read(){ int ans=0,f=1;char chr=getchar(); while(!isdigit(chr)){if(chr=='-') f=-1;chr=getchar();} while(isdigit(chr)) {ans=(ans<<3)+(ans<<1)+chr-48;chr=getchar();} return ans*f; } inline void kai(){ freopen("set.in","r",stdin); freopen("set.out","w",stdout); }long long a,b,c; int ksm(int x,int m){ if(m==1) return x; if(m==0) return 1ll; int t=ksm(x,m>>1);t=t*t%MOD; if(m&1) return t*x%MOD; return t; } signed main(){ // kai(); a=read(),b=read(),c=read(); int ans=ksm(2,c); cout<<ans; return 0; }
T2克拉克与数字
题目描述:
克拉克是一名人格分裂患者.某一天克拉克变成了一名数论研究者,在研究数字。
他想到了一个题:给定非负整数 x和正整数 k(1≤k≤2),可以做若干以下两种操作之一:
1. x=x-k
2. x=floor(sqrt(x))^2
现在克拉克想知道,这个整数最少经过多少次操作可以变成 0。
输入:
第一行是一个正整数T,表示数据组数。每组数据只有一行两个整数x, k。
输出:
每组数据输出一行一个整数,表示最少的操作数。若不存在方案,输出-1。
样例输入:
2
2 1
3 2
样例输出:
2
-1
数据规模:
30%:x≤100
50%:x≤2*10^9
100%: 1≤T≤100,0≤x≤10^18, 1≤k≤2
那个啥,精度误差了解一下...
当场打了一个搜索,暴力找规律,然后还真的找到了...
然而,爆搜打错了...每个都漏了1,然后输出的答案也漏了1...
正确思路好像是DP出小的数字答案,大的数字显然是要开方更划算的
Tip:
·注意精度误差,系统自带的sqrt可能对较大的数有些误差,所以要调整一下(或者手打二分也可以),反正我搞这个搞了好久...
·小的数(小于5)没规律,要打表
代码如下:
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #include<cmath> 6 #define int long long 7 using namespace std; 8 inline int read(){ 9 int ans=0,f=1;char chr=getchar(); 10 while(!isdigit(chr)){if(chr=='-') f=-1;chr=getchar();} 11 while(isdigit(chr)) {ans=(ans<<3)+(ans<<1)+chr-48;chr=getchar();} 12 return ans*f; 13 } 14 inline void kai(){ 15 freopen("clarke.in","r",stdin); 16 freopen("clarke.out","w",stdout); 17 } 18 int T,x,y,ans; 19 int dfs2(int x){ 20 if(x<0||x==1) return -1; 21 if(x==0) return 0; 22 if(x==2) return 1; 23 int p=floor(sqrt(x));p*=p; 24 if(p==x) return dfs2(x-2)+1; 25 int t1=dfs2(x-2),t2=dfs2(p); 26 if(t1==-1) return t2+1; 27 return min(t1,t2)+1; 28 } 29 inline int Sqrt(int n){ 30 int x=sqrt(n); 31 if (x*x==n)return x; 32 if (x*x>n){while(x*x>n)x--;return x;} 33 else{while((x+1)*(x+1)<n)x++;return x;} 34 } 35 signed main(){ 36 kai(); 37 T=read(); 38 while(T--){ 39 x=read(),y=read(); 40 if(y==1){ 41 if(x==0) {puts("0");continue;} 42 int k=Sqrt(x);k*=k; 43 if(k==x) 44 ans=2*Sqrt(x)-1; 45 else ans=2*Sqrt(x); 46 printf("%lld\n",ans); 47 }else{ 48 if(x==5) {puts("3");continue;} 49 if(x<5){ 50 if(x==1||x==3) {printf("-1\n");continue;} 51 printf("%lld\n",dfs2(x)); 52 } 53 else 54 { 55 int k=Sqrt(x);k*=k; 56 if(k==x||k+1==x){ 57 ans=2*Sqrt(x)-3; 58 }else{ 59 ans=2*Sqrt(x)-2; 60 } 61 printf("%lld\n",ans+1); 62 } 63 } 64 } 65 return 0; 66 }
T3电压
题目描述:
老胡的某个机房中有着复杂的电路。电路由n个节点和m根细长的电阻组成,节点被标号为1~N。
每个节点有一个可设定的状态【高电压】或者【低电压】。每个电阻连接两个节点,只有一端是高电压,另一端是低电压的电阻才会有电流流过。两端都是高电压或者低电压的电阻不会有电流流过。
某天,老胡为了维护电路,选择了一根电阻,为了能让【只有这根电阻上的电流停止流动,其他M-1根电阻中都有电流流过】,需要调节各节点的电压。为了满足这个条件,能选择的电阻共有多少根?
现在给出电路的信息,请你输出电路维护时可以选择使其不流的电阻的个数。
输入:
第一行两个空格分隔的正整数N和M,表示电路中有N个节点和M根电阻。
接下来M行,第i行有两个空格分隔的正整数Ai和Bi(1<=Ai<=N,1<=Bi<=N,Ai≠Bi),表示第i个电阻连接节点Ai和节点Bi。
输出:
输出一行一个整数,代表电路维护时可选择的使其不流的电阻个数。
样例输入:
4 4
1 2
2 3
3 2
4 3
样例输出:
2
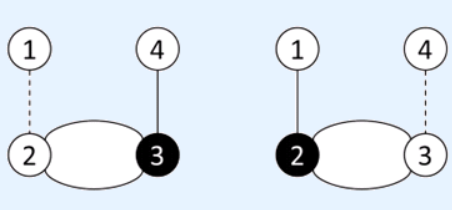
样例解释:
可以选择第一根电阻或第四根电阻。
数据规模:
50%:N<=1000,M<=2000
100%: 2<=N<=10^5,1<=M<=2*10^5
题目转换:
给一张图,需要删掉一条边后使其成为一张二分图,且删掉的边不能是二分图上的边,求满足条件的边数。
思路:找在所有奇数环上,且不在偶数环上的边。 对图dfs,差分统计即可。 (图上与环有关的问题可以使用类似tarjan的做法先dfs出一颗树,再对非树边进行处理)
1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<algorithm> 5 #include<map> 6 using namespace std; 7 char B[1<<15],*S=B,*T=B,ch; 8 #define getc() (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++) 9 inline int read(){ 10 int x=0; char ch=getc(); 11 while (ch<'0'||ch>'9') {ch=getc();} 12 while (ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+ch-'0'; ch=getc();} 13 return x; 14 } 15 inline void kai(){ 16 freopen("voltage.in","r",stdin); 17 freopen("voltage.out","w",stdout); 18 }const int M=2e5+5; 19 int n,m,fa[M],head[M<<1],ver[M<<1],nxt[M<<1],tot=1,d[M],odd[M],even[M],even_tot,odd_tot,ans; 20 inline void add(int x,int y){ver[++tot]=y;nxt[tot]=head[x];head[x]=tot;} 21 void dfs(int x,int l){ 22 for(int i=head[x];i;i=nxt[i]) if((i^1)!=l){ 23 int v=ver[i]; 24 if(d[v]){ 25 if(d[v]>d[x]) continue; 26 if((d[x]-d[v])&1)//奇数环 27 ++odd[x],--odd[v],++odd_tot;//记录差分(奇环) 28 else ++even[x],--even[v],++even_tot;//同上(偶环) 29 }else{ 30 d[v]=d[x]+1;//访问顺序 31 dfs(v,i);//继续向下 32 odd[x]+=odd[v];even[x]+=even[v]; 33 } 34 } 35 } 36 int main(){ 37 // kai(); 38 n=read(),m=read(); 39 for(int i=1;i<=m;++i){int x=read(),y=read();add(x,y),add(y,x);} 40 for(int i=1;i<=n;++i){if(!d[i]) d[i]=1,dfs(i,0),fa[i]=1;} 41 for(int i=1;i<=n;++i)if(!fa[i]&&even[i]==even_tot&&!odd[i]) ++ans; 42 if(even_tot==1) ++ans; 43 cout<<ans; 44 return 0; 45 }