03.四元数
四元数
单位四元数可以用来描述三维空间中的旋转,它既是紧凑的,也没有奇异性。
一个四元数描述唯一一个空间旋转,但是一个空间旋转可以由互为相反数的两个四元数表示。
1.四元数
-
四元数的定义
- 四元数是由四个元构成的数
- \(\boldsymbol{Q}(q_0,q_1,q_2,q_3) = q_0 + q_1\boldsymbol{i}+q_2\boldsymbol{j}+q_3\boldsymbol{k}\)
- \(q_0,q_1,q_2,q_3\)是实数,\(\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\)是满足如下条件的单位向量
- \(\boldsymbol{i}\otimes\boldsymbol{i}=-1,\boldsymbol{j}\otimes\boldsymbol{j}=-1,\boldsymbol{k}\otimes\boldsymbol{k}=-1\) 自己与自己进行四元数乘结果为-1。
- \(\boldsymbol{i}\otimes\boldsymbol{j}=\boldsymbol{k},\boldsymbol{j}\otimes\boldsymbol{k}=\boldsymbol{i},\boldsymbol{k}\otimes\boldsymbol{i}=\boldsymbol{j}\) 按照\(\boldsymbol{i}\rarr\boldsymbol{j}\rarr\boldsymbol{k}\rarr\boldsymbol{i}...\) 的顺序两两作四元数乘可以得到下一个。
- \(\boldsymbol{j}\otimes\boldsymbol{i}=\boldsymbol{-k},\boldsymbol{k}\otimes\boldsymbol{j}=\boldsymbol{-i},\boldsymbol{i}\otimes\boldsymbol{k}=\boldsymbol{-j}\) 按照\(\boldsymbol{i}\rarr\boldsymbol{j}\rarr\boldsymbol{k}\rarr\boldsymbol{i}...\) 相反的顺序两两作四元数乘可以得到下一个的负。
- \(\otimes\)表示四元数乘法
-
四元数的表达方式
-
矢量式
-
\(\boldsymbol{Q}=q_0+\boldsymbol{q}\)
其中\(q_0\)称四元数\(\boldsymbol{Q}\)的标量部分,\(\boldsymbol{q}\)称四元数\(\boldsymbol{Q}\)的矢量部分。\(\boldsymbol{q}\)是三维空间中的一个向量。
-
-
复数式
-
\(\boldsymbol{Q}=q_0+q_1\boldsymbol{i}+q_2\boldsymbol{j}+q_3\boldsymbol{k}\)
可视为一个超复数,\(\boldsymbol{Q}\)的共轭复数记为:
\(\boldsymbol{Q}^*=q_0-q_1\boldsymbol{i}-q_2\boldsymbol{j}-q_3\boldsymbol{k}\)
-
-
三角式
-
\(\boldsymbol{Q}=cos\frac{\theta}{2}+\boldsymbol{u}sin\frac{\theta}{2}\)
式中,\(\boldsymbol{u}\)为单位向量,即旋转轴。\(\theta\)为实数,即绕单位向量\(\boldsymbol{u}\)的旋转角度。
-
-
指数式
-
\(\boldsymbol{Q}=e^{\boldsymbol{u}\frac{\theta}{2}}\)
式中,\(\boldsymbol{u}\)和\(\theta\)同上。
-
-
矩阵式
- \({\boldsymbol{Q}}=\begin{bmatrix}q_0\\ q_1 \\ q_2 \\ q_3 \end{bmatrix}\)
-
-
四元数的大小—范数
-
四元数的大小用四元数的范数来表示:
\(||\boldsymbol{Q}||=q^2_0+q^2_1+q^2_2+q^2_3\)
-
\(||\boldsymbol{Q}||=1\),则\(\boldsymbol{Q}\)成为规范化四元数。描述旋转的四元数成为规范化四元数。规范化四元数参与旋转运动时要作归一化。
-
-
四元数的运算
-
加法和减法:对应实部和虚部相加/减
-
设
\(\boldsymbol{Q}=q_0+q_1\boldsymbol{i}+q_2\boldsymbol{j}+q_3\boldsymbol{k}\)
\(\boldsymbol{P}=p_0+p_1\boldsymbol{i}+p_2\boldsymbol{j}+p_3\boldsymbol{k}\)
则
\(\boldsymbol{Q}\pm\boldsymbol{P}=(q_0\pm p_0)+(q_1\pm p_1)\boldsymbol{i}+(q_2\pm p_2)\boldsymbol{j}+(q_3\pm p_3)\boldsymbol{k}\)
-
-
乘法:合并同类项(根据向量\(\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}\)向量相乘规则)
-
标量乘
\(a\boldsymbol{Q}=aq_0+aq_1\boldsymbol{i}+aq_2\boldsymbol{j}+aq_3\boldsymbol{k}\)
其中\(a\)为标量
-
四元数乘
\[\begin{align} P\otimes Q&=(q_0+q_1\boldsymbol{i}+q_2\boldsymbol{j}+q_3\boldsymbol{k})\otimes(p_0+p_1\boldsymbol{i}+p_2\boldsymbol{j}+p_3\boldsymbol{k})\\ &=(p_0q_0-p_1q_1-p_2q_2-p_3q_3)+(p_0q_1+p_1q_0+p_2q_3-p_3q_2)\boldsymbol{i}+(p_0q_2+p_2q_0+p_3q_1-p_1q_3)\boldsymbol{j}+(p_0q_3+p_3q_0+p_1q_2-p_2q_1)\boldsymbol{k}\\ &=r_0+r_1\boldsymbol{i}+r_2\boldsymbol{j}+r_3\boldsymbol{k} \end{align} \]-
写成矩阵形式
-
\[\begin{bmatrix}r_0\\ r_1\\ r_2 \\ r_3\end{bmatrix}=\begin{bmatrix}p_0&-p_1&-p_2&-p_3\\ p_1&p_0&-p_3&p_2 \\ p_2&p_3&p_0&-p_1\\p_3&-p_2&p_1&p_0\end{bmatrix}\begin{bmatrix}q_0\\ q_1\\ q_2 \\ q_3\end{bmatrix}=\boldsymbol{M(P)Q} \]
或
\[\begin{bmatrix}r_0\\ r_1\\ r_2 \\ r_3\end{bmatrix}=\begin{bmatrix}q_0&-q_1&-q_2&-q_3\\ q_1&q_0&q_3&-q_2 \\ q_2&-q_3&q_0&q_1\\q_3&q_2&-q_1&q_0\end{bmatrix}\begin{bmatrix}p_0\\ p_1\\ p_2 \\ p_3\end{bmatrix}=\boldsymbol{M^{'}(Q)P} \]-
注意:
-
四元数乘法不满足交换律
- \(P\otimes Q=\boldsymbol{M(P)Q}\ne\boldsymbol{M^{'}(P)Q}=Q\otimes P\)
-
四元数乘法满足分配律和结合律
- \(P\otimes (Q+R)=P\otimes Q + P\otimes R\)
- \(P\otimes Q\otimes R=(P\otimes Q)\otimes R=P\otimes (Q\otimes R)\)
-
此外,还有
- \((P\otimes Q)^*=Q^*\otimes P^*\)
证明,略。
-
-
除法—求逆
\(P\otimes P^* =||P||\)
\(P\otimes\frac{\boldsymbol{P}^*}{||\boldsymbol{P}||}=1\)
所以:
\(\boldsymbol{P}^{-1}=\frac{\boldsymbol{P}^*}{||\boldsymbol{P}||}\)
-
2.四元数和姿态矩阵之间的关系
-
根据四元数的三角式 \(\boldsymbol{Q}=cos\frac{\theta}{2}+\boldsymbol{u}sin\frac{\theta}{2}\) ,\(\boldsymbol{u}\)为单位向量,即旋转轴。\(\theta\)为实数,即绕单位向量\(\boldsymbol{u}\)的旋转角度。(证明可见《惯性导航》 秦永元 第二版)
-
四元数与旋转矩阵(略)
-
坐标变换的四元数乘表示法
- \(\boldsymbol{r}^n=\boldsymbol{Q}\otimes \boldsymbol{r}^b\otimes \boldsymbol{Q}^*\)
其中\(\boldsymbol{Q}\)为\(b\)系至\(n\)系的旋转四元数,等价于:
- \(\boldsymbol{r}^n=\boldsymbol{C}^n_br^b\)
有时为了简单记向量变换会被用四元数的方式记为 \(\boldsymbol{r}^n=\boldsymbol{q}_{nb}b\) 甚至Eigen矩阵运算库也支持这样的表达式求解,但是在实际运算时任然要根据四元数的乘法表示法来运算
3.四元数微分方程
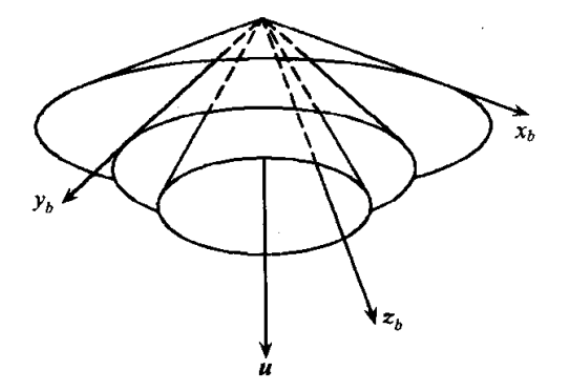
\(b\)坐标系绕\(\boldsymbol{u}\)轴旋转时形成的三个圆锥面
\(\boldsymbol{Q}\)为表征由\(n\)系至\(b\)系的旋转四元数:
\(\boldsymbol{Q}=cos\frac{\theta}{2}+\boldsymbol{u}sin\frac{\theta}{2}\)
上式两边求导
\(\frac{d\boldsymbol{Q}}{dt}=-\frac{\dot{\theta}}{2}sin\frac{\theta}{2}+\boldsymbol{u}^n\frac{\dot{\theta}}{2}cos\frac{\theta}{2}+sin\frac{\theta}{2}\frac{d\boldsymbol{u}^n}{dt}\)
其中:
\(\frac{d\boldsymbol{u}^n}{dt}=\frac{d\boldsymbol{u}}{dt}|^n_n=R^n_b\frac{d\boldsymbol{u}}{dt}|^b_b+\omega^n_{nb}×\boldsymbol{u}^n\)
由于刚体绕\(\boldsymbol{u}\)旋转,与刚体固联的\(b\)坐标系各轴在旋转过程中分别为与三个不同的圆锥平面上,圆锥顶点即为坐标原点,\(\boldsymbol{u}\)在\(b\)坐标系内观察始终未变,即有:
\(\frac{d\boldsymbol{u}}{dt}|^b_b=\boldsymbol{0}\)
又由于:
\(\omega^n_{nb}=\dot{\theta}\boldsymbol{u}^n\)
所以:
\(\frac{d\boldsymbol{u}^n}{dt}=R^n_b\frac{d\boldsymbol{u}}{dt}|^b_b+\dot{\theta}\boldsymbol{u}^n×\boldsymbol{u}^n=\boldsymbol{0}\)
因此:
\(\frac{d\boldsymbol{Q}}{dt}=-\frac{\dot{\theta}}{2}sin\frac{\theta}{2}+\boldsymbol{u}^n\frac{\dot{\theta}}{2}cos\frac{\theta}{2}\)
又由于
\(\frac{\dot{\theta}}{2}\boldsymbol{u}^n\otimes \boldsymbol{Q}=\frac{\dot{\theta}}{2}\boldsymbol{u}^n\otimes (cos\frac{\theta}{2}+\boldsymbol{u}^nsin\frac{\theta}{2})=\frac{\dot{\theta}}{2}cos\frac{\theta}{2}\boldsymbol{u}^n+\boldsymbol{u}^n\otimes \boldsymbol{u}^n\frac{\dot{\theta}}{2}sin\frac{\theta}{2}\)
\(\boldsymbol{u}^n\otimes \boldsymbol{u}^n=-1\)
所以
\(\frac{\dot{\theta}}{2}\boldsymbol{u}^n\otimes \boldsymbol{Q}=\frac{\dot{\theta}}{2}\boldsymbol{u}^ncos\frac{\theta}{2}-\frac{\dot{\theta}}{2}sin\frac{\theta}{2}\)
在捷联惯导中我们能直接测量的是机体坐标系(b)下的旋转,因此还有如下转换下:
\(\omega^n_{nb}=\boldsymbol{Q}\otimes\omega^b_{nb}\otimes\boldsymbol{Q}^*\)
代入上式得:
- 简单推导
根据四元数的三角式表达
当旋转一小段时间,即角度趋于0时,容易有:
上式在表示旋转时记得要进行归一化.
其中\(\boldsymbol{\delta\theta}\)的方向表示旋转轴,模长表示旋转的角度
角速度:
根据由导数的定义,四元数对时间求导(右乘扰动模型):


