02.旋转向量和欧拉角

旋转向量和欧拉角

1.旋转向量

SO(3)的旋转矩阵有9个量，但是只有3个自由度，并且是单位正交矩阵，具有冗余性，对其估计或优化问题的求解不方便，SE(3)的变换矩阵也有类似的问题。我们可以用一个旋转轴和一个旋转角描述任意旋转。一个方向与旋转轴一致，长度（模）等于旋转角的向量，我们称之为旋转向量(或轴角)。同样，对于变换矩阵，我们可以用一个三维的旋转向量和一个平移向量表达。

• 旋转向量到旋转矩阵(Rodrigues’s Formula)

  \(\boldsymbol{n}\)为旋转轴，\(\theta\)为旋转角，\(\boldsymbol{R}\)为相应的旋转矩阵，为旋转后的坐标系在原坐标系下的表达

  \[\boldsymbol{R}=cos\theta\boldsymbol{I}+(1-cos\theta)\boldsymbol{n}\boldsymbol{n}^T+sin\theta \hat{\boldsymbol{n}} \]

  或者:

  \[\boldsymbol{R}=\boldsymbol{I}+sin\hat{\boldsymbol{n}}+(1-cos\theta)\hat{\boldsymbol{n}}\hat{\boldsymbol{n}} \]

  其中^是向量的反对称转换符:

  \[\hat{\boldsymbol{n}}=\begin{bmatrix}0&-n_z&n_y\\ n_z&0&-n_x \\ -n_y&n_x&0\end{bmatrix} \]

  (1)和(2)两个公式是等价的，其中公式(1)是高博在《视觉SLAM十四讲》中用到的形式

• 旋转矩阵到旋转向量转

  • 旋转角度：
  \[\begin{align} tr(\boldsymbol{R})&=cos\theta tr((\boldsymbol{I}))+(1-cos\theta)tr(\boldsymbol{n}\boldsymbol{n}^T)+sin\theta tr(\hat{\boldsymbol{n}})\\ &=3cos\theta + (1-cos\theta)\\ &=1+2cos(\theta) \end{align} \]

  ​ 所以:

  \[\theta = arccos(\frac{tr(\boldsymbol{R}-1)}{2})) \]

  • 旋转向量：

    方法一：关于旋转轴\(\boldsymbol{n}\)，由于旋转轴上的向量在旋转之后不发生改变，则有：

    \[\boldsymbol{R}\boldsymbol{n} = \boldsymbol{n} \]

    因此旋转轴\(\boldsymbol{n}\)是矩阵\(\boldsymbol{R}\)特征值对应的特征向量。求解此方程，再归一化，就得到了旋转轴。

    方法二：根据轴角表达的物理含义

    \[\boldsymbol{R}^T=cos\theta\boldsymbol{I}+(1-cos\theta)\boldsymbol{n}\boldsymbol{n}^T-sin\theta \hat{\boldsymbol{n}} \]

    所以：

    \[\hat{\boldsymbol{n}} = \frac{\boldsymbol{R} - \boldsymbol{R}^T}{2sin\theta} \]

2.欧拉角

对于轴角表示情况,转轴具有2个自由度,转角1个自由度。实 际上，一个一般的转动可分解为三个基本转动的复合。基本转动是 指以坐标轴为转轴的转动,相当于选取“固定”的转轴，这样，转轴不再具有自由度，3个自由度通过3个转角表示,这就是欧拉角。 根据三次基本转动选取的坐标轴的不同，欧拉角共有12种组合。如 果再考虑到可选取原始坐标系的坐标轴，也可选取“新”坐标系的坐标轴，则共有24种欧拉角表示。一般规定原始坐标系为静坐标系，每个基本转动后形成的新坐标系为动坐标系。

• 24 种欧拉角表示列举如下：

  • 静轴(即转轴选静坐标系的坐标轴):
    \(sXYZ,sXZY, sXYX, sXZX, sYXZ, sYZX,\)
    \(sYXY, sYZY, sZXY, sZYX, sZXZ, sZYZ\)

  • 动轴(即转轴选动坐标系的坐标轴):

    \(rZYX, rYZX, rXYX, rXZX, rZXY, rXZY,\)
    \(rYXY, rYZY, rYXZ, rXYZ, rZXZ, rZYZ\)

• 静轴欧拉角和动轴欧拉角有如下规律:

  绕静轴 \(XYZ\) 分别 转 \(α , β , γ\) 角度的转动与绕动轴 $ZYX $分别转 \(γ , β , α\) 角度的转动等 价，其他形式的欧拉角亦有此类似规律。

我们以导航中常用的动轴\(rZYX\) （即：偏航(yaw)->俯仰(pitch)->滚转(roll))为例，说明下由欧拉角到旋转矩阵的转换过程。

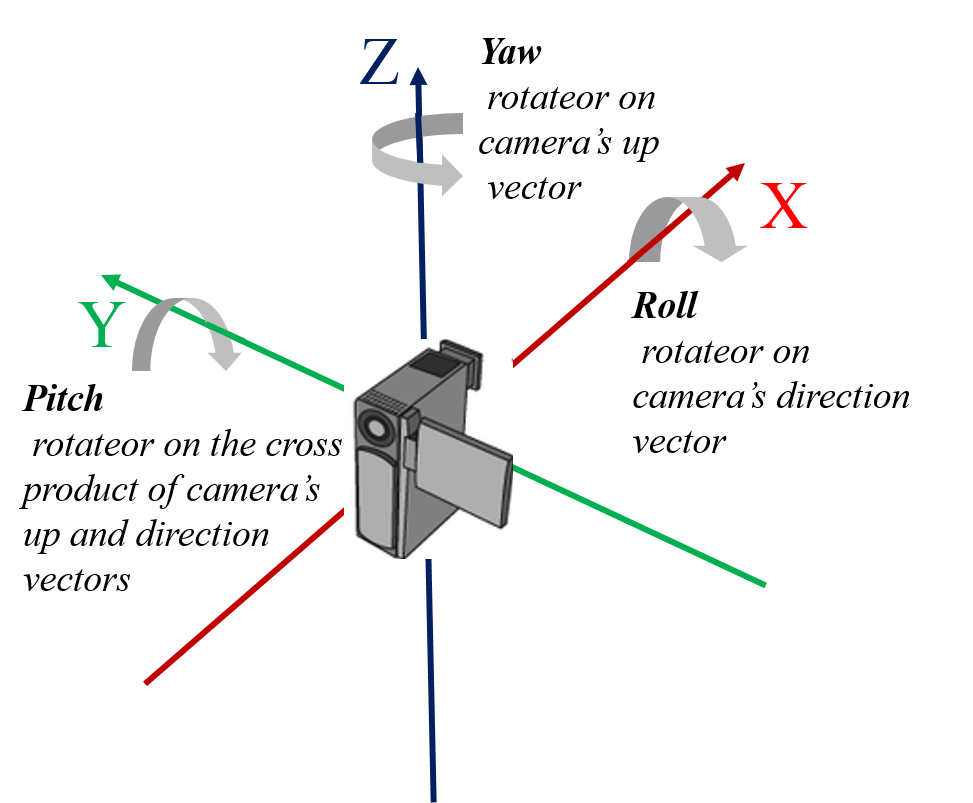
对于不同的坐标系定义，有不同的转换关系。我们只讨论常用的一种情况：如上图，右手系，Z轴朝上，X轴朝前，y轴朝左。绕Z轴作偏航（Yaw）运动，绕Y轴作俯仰（Pitch）运动，绕X轴作滚转（Roll）运动，运动正方向如上图所示。

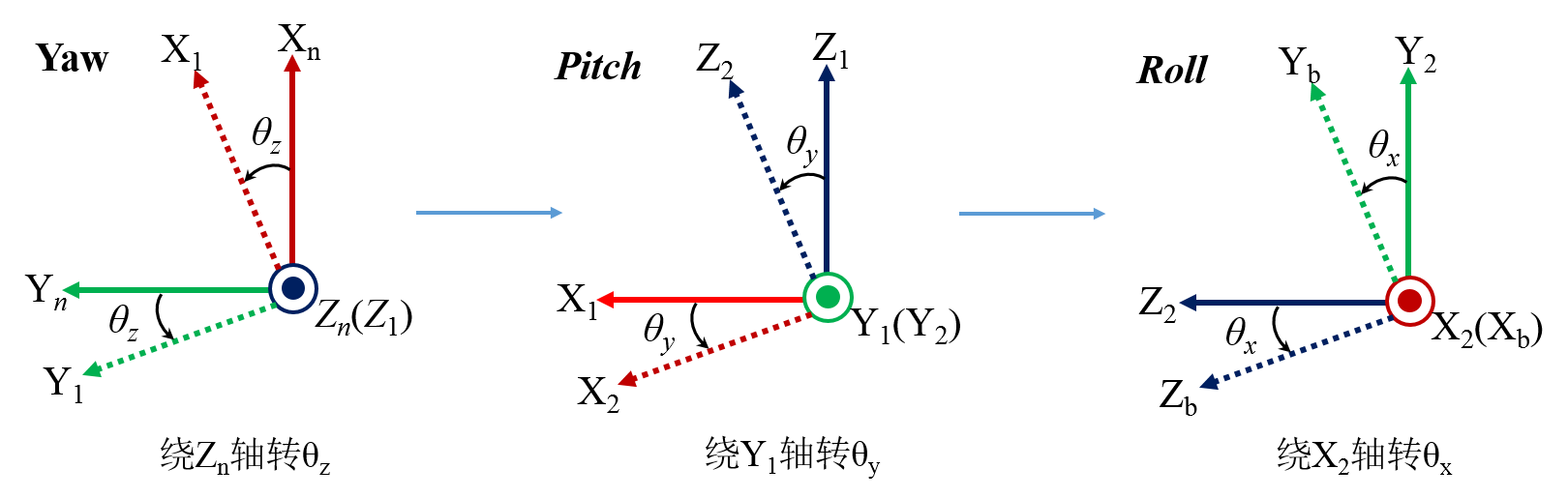
称仅绕一根轴的旋转为基本旋转，两坐标系之间任何复杂的角位置关系都可以看作有限次基本旋转的复合，变换矩阵等于基本旋转矩阵确定的变换矩阵的连乘，连乘顺序依基本旋转的先后次序由右向左排列。上图描述了由坐标系n经过偏航、俯仰和滚转三次基本旋转到坐标系b，得到\(R_b^n\)

\(R_1^n\)代表了经过一次偏航后坐标系1在坐标系n下的姿态描述（投影）:

\[\begin{align} R_z=R_1^n=\begin{bmatrix}\cos\theta_z & -\sin\theta_z & 0 \\\sin\theta_z & \cos\theta_z & 0 \\0 & 0 & 1 \\\end{bmatrix} \end{align} \]

\(R_2^1\)代表了经过一次俯仰后坐标系2在坐标系1下的姿态描述（投影）:

\[\begin{align} R_y=R_2^1=\begin{bmatrix}\cos\theta_y & 0 & \sin\theta_y \\0 & 1 & 0 \\-\sin\theta_y & 0 & \cos\theta_y \\\end{bmatrix} \end{align} \]

\(R_b^2\)代表了经过一次滚转后坐标系b在坐标系2下的姿态描述（投影）:

\[\begin{align} R_x=R_b^2=\begin{bmatrix}1 & 0 & 0 \\0 & \cos\theta_x &-\sin\theta_x \\0 & \sin\theta_x & \cos\theta_x \\\end{bmatrix} \end{align} \]

对于列向量的变换，连乘顺序依基本旋转的先后次序由右向左排列：

\[R_b^n=R_1^n\cdot R_2^1 \cdot R_b^2=R_z\cdot R_y \cdot R_x \]

上式中\(R_b^n\)与旋转次序有关，即当\(\theta_z\)，\(\theta_y\)，\(\theta_x\)不都为小角时，对应于不同的旋转次序，空间坐标系b的最终位置时不同的，这就是有限转动的不可交换性。但是当\(\theta_z\)，\(\theta_y\)，\(\theta_x\)都为小角时，忽略小角间的高阶小量：

当\(\Delta x \rightarrow 0\),\(cos\Delta x \rightarrow1\)，\(sin\Delta x \rightarrow\Delta x\)

\[\begin{align} R_b^n\approx\begin{bmatrix}1 & -\theta_z & \theta_y \\ \theta_z & 1 & -\theta_x \\ -\theta_y & \theta_x & 1 \\\end{bmatrix} \end{align} \]

其中\(\theta_z\)，\(\theta_y\)，\(\theta_x\)角度为弧度，此时\(\theta_z\)，\(\theta_y\)，\(\theta_x\)构成的列向量\([\theta_z，\theta_y，\theta_x]^T\)可视为三维空间的（旋转）矢量，此时旋转后的坐标系的最终角位置与旋转次序无关：无限转动与旋转次序无关