A Simple Chess---hdu5794（容斥+Lucas）

题目链接：http://acm.split.hdu.edu.cn/showproblem.php?pid=5794

题意：给你一个n*m的网格，问从(1, 1)走到(n, m)的方案数是多少，其中有r个点是不可到达的；

根据公式我们可以知道每次只能走”日"型；

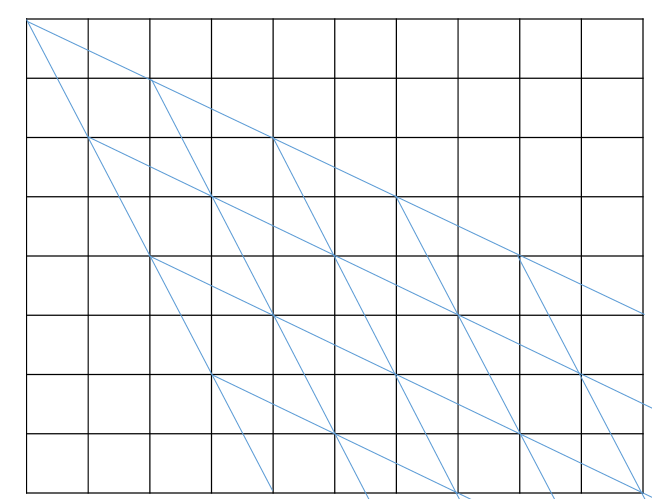
路径如上图所示，我们可以看到有很多点是不可达的,可达点都是满足(x+y)%3=2的;路径可以看成一个斜着放置的杨辉三角。我们只需要把坐标转换一下即可，这是没有障碍时的方案数；

让(1,1)到(n,m)中如果有一个障碍，那么我们可以用起点到终点的方法数-起点到障碍点的方法数*障碍点到终点的方法数；同样如果有 r 个，那就减去r次这样的情况；

同样处理到达每个点的时候也是这样处理的；

注意有不可达的，所以判断一下不然会re的；

#include<iostream>
#include<algorithm>
#include<string.h>
#include<stdio.h>
#include<math.h>
using namespace std;
#define N 120000
#define PI 4*atan(1.0)
#define mod 110119
#define met(a, b) memset(a, b, sizeof(a))
typedef long long LL;

struct node
{
    LL x, y;
    friend bool operator < (node p, node q)
    {
        if(p.x!=q.x)
            return p.x < q.x;
        return p.y < q.y;
    }
}a[105];

LL f[N] = {1};

LL Pow(LL a, LL b)
{
    LL ans = 1;
    while(b)
    {
        if(b&1)
            ans = ans*a%mod;
        b/=2;
        a = a*a%mod;
    }
    return ans%mod;
}

LL C(LL n, LL m)
{
    if(m>n)return 0;
    if(m == 0)return 1;
    LL ans = f[n] * Pow(f[m], mod-2)%mod * Pow(f[n-m], mod-2) % mod;
    return ans;
}
LL Lucas(LL n, LL m)
{
    if(n<0 || m<0)return 0;///会出现不可达的情况，所以注意判断，否则会re；
    if(m > n) return 0;
    if(m == 0) return 1;
    return C(n%mod, m%mod) * Lucas(n/mod, m/mod) % mod;
}

LL solve(LL x1, LL y1, LL x2, LL y2)
{
    if((x1+y1)%3 != 2)return 0;
    if((x2+y2)%3 != 2)return 0;

    LL ax = (x1+y1-2)/3;
    LL ay = y1 - 1 - ax;

    LL bx = (x2+y2-2)/3;
    LL by = y2 - 1 - bx;

    return Lucas(bx-ax, by-ay);
}


int main()
{
    for(int i=1; i<=110119; i++)
        f[i] = f[i-1]*i % mod;

    LL n, m;
    int t = 1, r;
    while(scanf("%I64d %I64d %d", &n, &m, &r)!=EOF)
    {
        LL ans[N];///起点到i的方案数；

        for(int i=1; i<=r; i++)
            scanf("%I64d %I64d", &a[i].x, &a[i].y);

        sort(a+1, a+r+1);///按x的升序排列，再按y的升序排列；

        LL sum = solve(1, 1, n, m);

        for(int i=1; i<=r; i++)
        {
            ans[i] = solve(1, 1, a[i].x, a[i].y);
            for(int j=1; j<i; j++)
            {
                ans[i] = ((ans[i] - ans[j]*solve(a[j].x, a[j].y, a[i].x, a[i].y)%mod) + mod) % mod;
            }
        }
        for(int i=1; i<=r; i++)
        {
            sum = (sum - ans[i]*solve(a[i].x, a[i].y, n, m)%mod + mod) % mod;
        }
        printf("Case #%d: %I64d\n", t++, sum);
    }
    return 0;
}