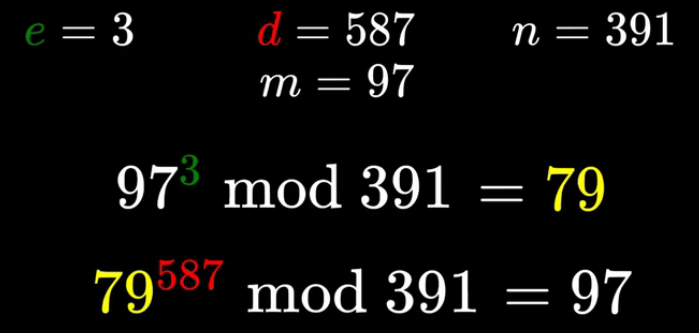公钥加密算法 RSA

到一个B站视频讲解，觉得很清晰，就想记录一下

 

原始数据：m

加密数据：c

 

 

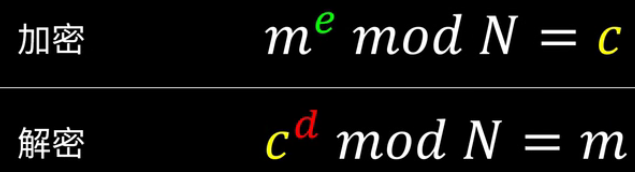
由 m^e mod N = c  得  m^e = Nt + c，即 c = m^e  - Nt . 然后带入 c^d mod N = m 得  (m^e  - Nt)^d mod N = m。

(m^e  - Nt)^d展开后只有第一项不包含N，其他项对N求余之后都为0，所以只保留m^ed。因此可得到下面变换。

 

 

 

 

             

 

 

 

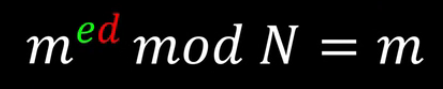
将欧拉定理进行变换

 

 

 

 

 

 

 

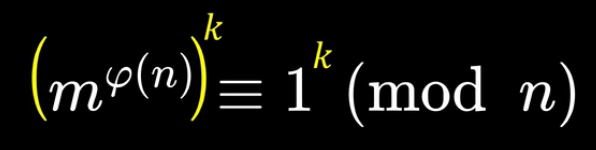
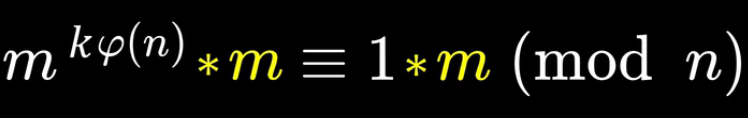
得到

 

 

 与之前的公式放一起

 

 

 

 

可以得到，

 

 

 

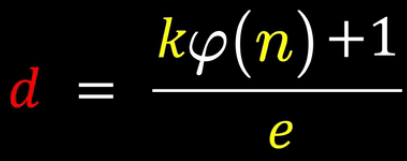
k为任意常数，n为了方便计算欧拉值，取质数

 

 

欧拉函数的性质：

 

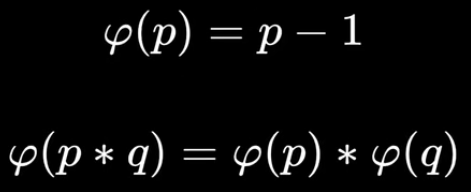
其中p为任意质数，p和q互质 

 

例如：

 

 

 

 

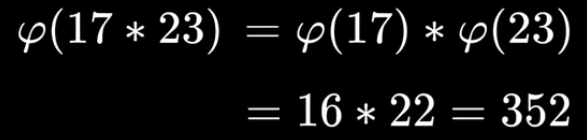
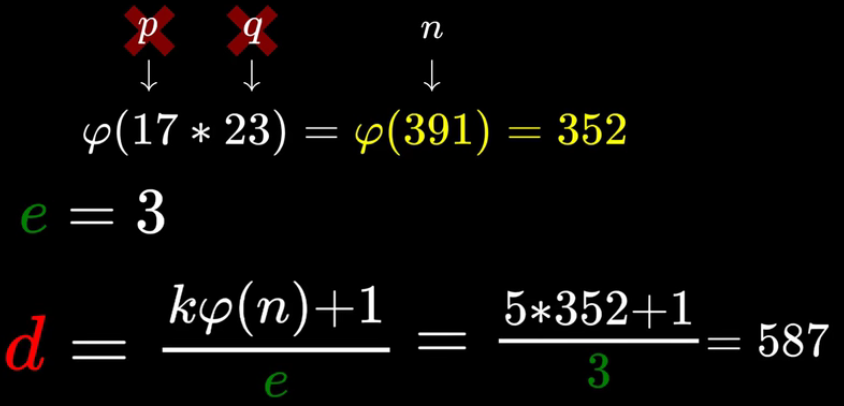
 其中选取的公钥e与φ(n)互质（这里不太清楚为什么），然后选取k值，这里的e为3，k为5, 可以计算取私钥d

 

公钥：(e,n)

私钥：d

 

因为攻击者不知道 p 和 q，所以无法计算出来φ(n)（因为大数分解质因子是困难的）因此无法得到私钥 d

 

利用上述信息进行RSA举例：对字符 ‘a’进行加解密