DNA sequence HDU - 1560
DNA sequence
Time Limit: 15000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4217 Accepted Submission(s): 2020
Problem Description
The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.
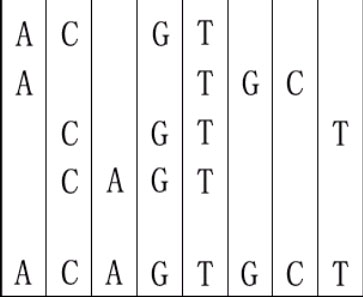
For example, given "ACGT","ATGC","CGTT" and "CAGT", you can make a sequence in the following way. It is the shortest but may be not the only one.

Input
The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.
Output
For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.
Sample Input
1
4
ACGT
ATGC
CGTT
CAGT
Sample Output
8
Author
LL
Source
Recommend
LL
题意:现在我们给定了数个DNA序列,请你构造出一个最短的DNA序列,使得所有我们给定的DNA序列都是它的子序列。例如,给定"ACGT","ATGC","CGTT","CAGT",你可以构造的一个最短序列为"ACAGTGCT",但是需要注意的是,这并不是此问题的唯一解。
思路: *IDA 若当前长度+最长构造长度< 迭代的最大深度则return 进行良好剪枝
accode
#include<iostream> #include<cstdio> #include<cstdlib> #include<sstream> #include<cstring> #include<string> #include<vector> #include<set> #include<stack> #include<queue> #include<map> #include<cmath> #include<algorithm> using namespace std; #define inf 0x3f3f3f3f #define ll long long #define MAX_N 1000005 #define gcd(a,b) __gcd(a,b) #define mem(a,x) memset(a,x,sizeof(a)) #define mid(a,b) a+b/2 #define stol(a) atoi(a.c_str())//string to long string temp[10]; string c = "ACGT"; int pos[10]; int len[10]; int deep; int n; int ans(){ int maxn = 0; for(int i = 0; i < n; i++){ maxn = max(maxn,len[i]-pos[i]); } return maxn; } int dfs(int step){ if(step + ans() > deep) return 0; if(!ans())//满足构造序列包含所有序列 return 1; int temp1[10]; for(int i = 0; i < 4; i++){ int flag = 0; for(int j = 0; j < n; j++) temp1[j] = pos[j]; for(int j = 0; j < n; j++){ if(temp[j][pos[j]] == c[i]){ flag = 1; pos[j]++; } } if(flag){ if(dfs(step+1)) return 1; for(int j = 0; j < n; j++) pos[j] = temp1[j]; } } return 0; } int main(){ // freopen("D:\\in.txt","r",stdin); int T; scanf("%d",&T); while(T--){ scanf("%d",&n); deep = 0; for(int i = 0; i < n; i++){ cin>>temp[i]; len[i] = temp[i].length(); pos[i] = 0; deep = max(deep,len[i]); } while(1){ if(dfs(0)) break; ++deep; } printf("%d\n",deep); } return 0; }


