常用极限定理

1.数列运算法则

假设 \(lim_{x \to \infty}x_n=a\) , \(lim_{y \to \infty}y_n=b\)

（1）\(lim_{n \to \infty} (x_n+y_n)=lim_{n \to \infty}x_n+lim_{n \to \infty y_n}=a+b\)（减法，乘法同）

（2） \(lim_{n \to \infty} \frac{x_n}{y_n} =\frac{lim_{n \to \infty} x_n}{lim_{n \to \infty} y_n}=\frac{a}{b} (lim_{n \to \infty}y_n=b \neq 0)\)

（3）\(lim_{n \to \infty }\sqrt{x_n}=\sqrt{lim_{n \to \infty }x_n}=\sqrt{a} (x_n \geq 0,a \geq 0)\)

2.函数运算法则

基本等同数列运算法则

拓展

\(lim f(x)^n =[lim f(x)]^n\)

\(lim (k*f(x))=k* lim f(x)\)

3.有关函数极限定理

定理1： \(lim_{x \to \infty} f(x)=A\) 的充要条件是 \(lim_{x \to +\infty}f(x)=lim_{x \to -\infty}f(x)=A\)

定理2：函数 \(f(x)\) 当 $x \to x_0 $ 时极限存在的充分必要条件是左极限及右极限各自存在且相等，此定理可以用来证明函数极限不存在。

4.两边夹定理（夹逼定理）

准则1（数列） 如果数列 \({x_n},{y_n},{z_n}\) 满足下列条件：

（1）\(y_n \leq x_n \leq z_n(n=N+1,N+2,...，N为自然数)\)

（2）\(lim_{n \to \infty }y_n=lim_{n \to \infty }z_N=a\),

则 \(lim_{n \to \infty} x_n\) 存在，且为 \(a\) 。

准则2（函数） 等同准则1,把范围拓广即可。

5.单调有界收敛定理

准则1：单调有界数列必有极限。

（1）单调递增有上界数列必有极限。

（2）单调递减有下界数列必有极限。

故求解数列极限可分三个步骤：证单调，证有界，列方程求极限（对递推式两边同时区极限，即假定 \(x_n=x_{n-1}\) ）。

6.两个重要极限

第一重要极限

\(lim_{x \to 0} \frac{sin x}{x} =1\)

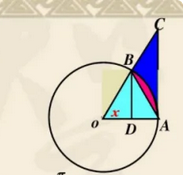
证明：在单位圆中，如图所示,设 \(\angle AOB=x(0 < x < \frac{\pi}{2})\) 则 \(BD=sinx,AC=tanx,\overset{\LARGE{\frown}}{AB}=x.\)

因为 \(S_{\triangle AOB} < S_{扇形AOB} < S_{\triangle AOC}\),即 $ sinx < x <tanx$.

故 \(cosx < \frac{sinx}{x} < 1\)

根据两边夹定理： \(lim_{x \to 0} 1 =lim_{x \to 0} {cosx}=1\) ,得 \(lim_{x \to 0} \frac{sinx}{x}=1\) .

第二重要极限

\(lim_{x \to \infty}(1+\frac{1}{x})^{x}=e\)

证明：首先利用二项式定理可以证明数列 \(x_n=(1+\frac{1}{n})^n\) 一定为单调有界的数列（直接二项式定理,然后拆出来每一项即可）,所以 \(x_n=(1+\frac{1}{n})^n\) 存在极限。

于是我们定义 \(lim_{n \to \infty} (1+ \frac{1}{n})^n\) 的极限的值记为 \(e\) ，这个值即自然对数 \(y=lnx\) 的底。该数列的极限可以推广到函数。

变式：\(lim_{x \to \infty} (1+x)^{\frac{1}{x}}=e\)

第二重要极限的特征：为 \(1^{\infty}\) 型，即指数的极限为 \(\infty\) 。

推论1：

\(lim_{x \to 0} \frac{ln(1+x)}{x}=1\)

证明： \(lim_{x \to 0} \frac{ln(1+x)}{x}=lim_{x \to 0} ln(1+x)^{\frac{1}{x}}=ln lim_{x \to 0}(1+x)^{\frac{1}{x}}=ln e=1\)

推论2：

\(lim_{x \to 0}\frac{e^x-1}{x}=1\)

证明：令 \(y=e^x-1\) ，因为 \(x \to 0\)，所以 \(y \to 0\) ，则 \(x=In(1+y)\).

将式子代换得： \(lim_{y \to 0}\frac{y}{In(1+y)}=lim_{y \to 0}\frac{1}{\frac{In(1+y)}{y}}=1\)