ForkJoin

ForkJoinPool 是 JDK 7 中，@author Doug Lea 加入的一个线程池类。Fork/Join 框架的核心原理就是分治算法（Divide-and-Conquer）和工作窃取算法（work-stealing algorithm）。

Fork分解任务成独立的子任务，用多线程去执行这些子任务，Join合并子任务的结果。这样就能使用多线程的方式来执行一个任务。

JDK7引入的Fork/Join有三个核心类：

• ForkJoinPool，执行任务的线程池。
• ForkJoinWorkerThread，执行任务的工作线程。
• ForkJoinTask，一个用于ForkJoinPool的任务抽象类。它提供了很多方法，但核心的是fork()和join()方法，承载着主要的任务协调工作，fork()用于任务提交，join()用于结果获取。

因为ForkJoinTask比较复杂，抽象方法比较多，日常使用时一般不会继承ForkJoinTask来实现自定义的任务，而是继承ForkJoinTask的两个子类：

• RecursiveTask：子任务带返回结果时使用。
• RecursiveAction：子任务不带返回结果时使用。

ForkJoinPool 最适合的是计算密集型的任务，如果存在 I/O，线程间同步，sleep() 等会造成线程长时间阻塞的情况时，最好配合使用 ManagedBlocker。

ForkJoinPool 分治算法思想

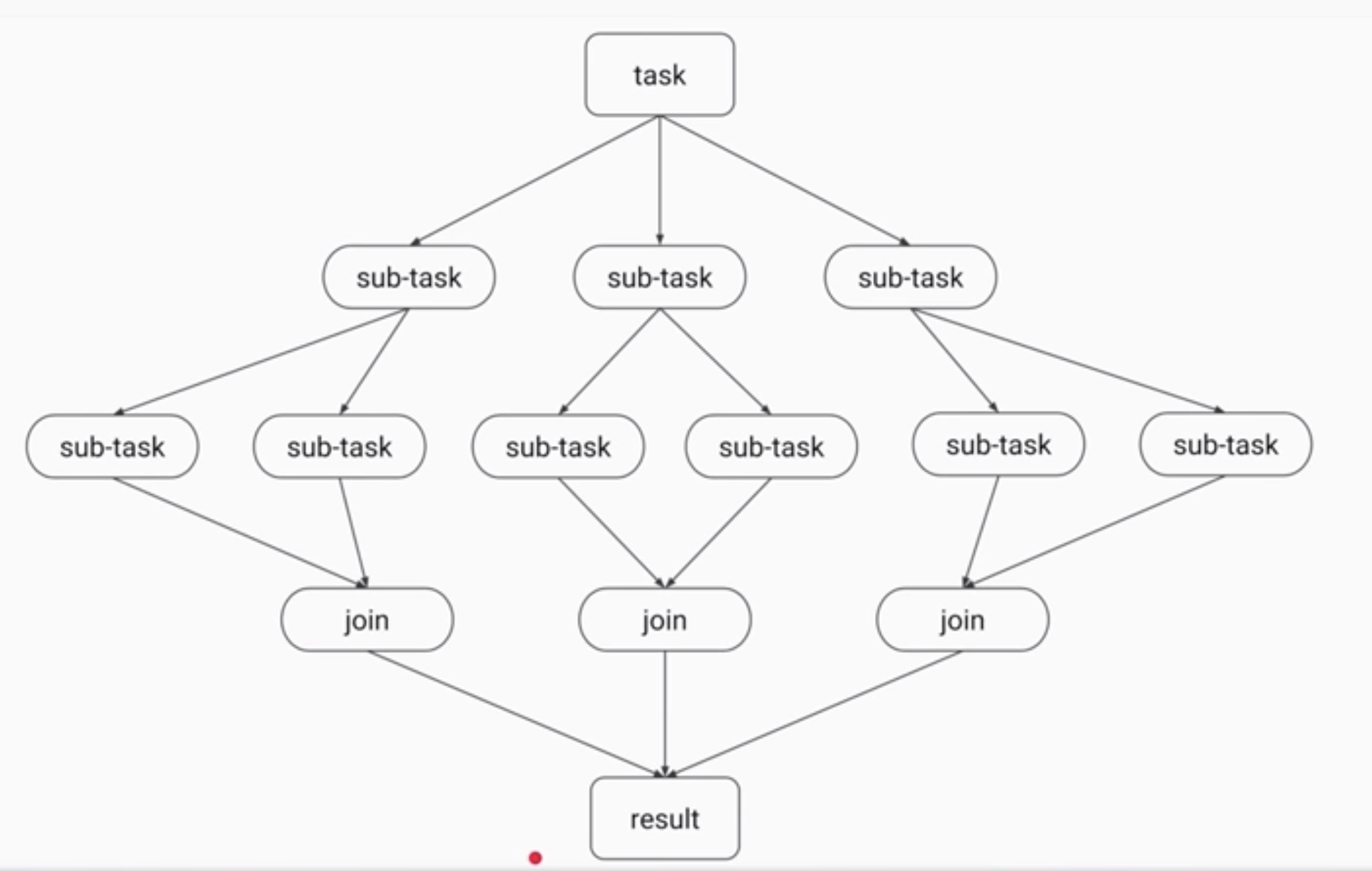
分治（divide and conquer），也就是把一个复杂的问题分解成相似的子问题，然后子问题再分子问题，直到问题分的无法再划分了。然后层层返回子问题的结果，最终合并返回问题结果。

分治在算法上有很多应用，类似大数据的MapReduce，归并算法、快速排序算法等。JUC中的Fork/Join的并行计算框架类似于单机版的 MapReduce。

我们常用的数组工具类 Arrays 在JDK 8之后新增的并行排序方法（parallelSort）就运用了 ForkJoinPool 的特性，还有 ConcurrentHashMap 在JDK 8之后添加的函数式方法（如forEach等）也有运用。在整个JUC框架中，ForkJoinPool 相对其他类会复杂很多。

工作窃取算法（work-stealing）

ForkJoinPool 的核心特性是它使用了work-stealing（工作窃取）算法：线程池内的所有工作线程都尝试找到并执行已经提交的任务，或者是被其他活动任务创建的子任务（如果不存在就阻塞等待）。

这种特性使得 ForkJoinPool 在运行多个可以产生子任务的任务，或者是提交的许多小任务时效率更高。尤其是构建异步模型的 ForkJoinPool 时，对不需要合并（join）的事件类型任务也非常适用。

• 工作窃取算法的优点是充分利用线程进行并行计算，从尾部窃取任务减少了线程间的竞争。
• 工作窃取算法缺点是在某些情况下还是存在竞争，比如双端队列里只有一个任务时。并且消耗了更多的系统资源，比如创建多个线程和多个双端队列。

在 ForkJoinPool 中，线程池中每个工作线程（ForkJoinWorkerThread）都对应一个任务队列（WorkQueue），工作线程优先处理来自自身队列的任务（LIFO或FIFO顺序，参数 mode 决定），然后以FIFO的顺序随机窃取其他队列中的任务。

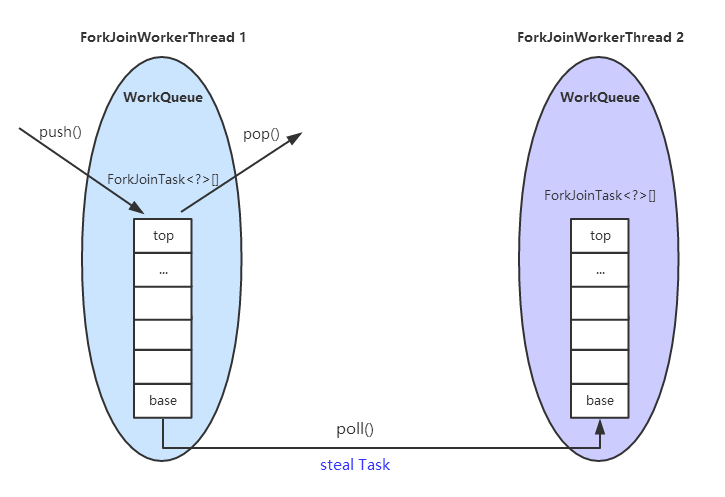
ForkJoinPool 中的任务分为两种：一种是本地提交的任务（Submission task，如 execute、submit 提交的任务）；另外一种是 fork 出的子任务（Worker task）。两种任务都会存放在 WorkQueue 数组中，但是这两种任务并不会混合在同一个队列里，ForkJoinPool 内部使用了一种随机哈希算法（有点类似 ConcurrentHashMap 的桶随机算法）将工作队列与对应的工作线程关联起来，Submission 任务存放在 WorkQueue 数组的偶数索引位置，Worker 任务存放在奇数索引位。

示例

public class LongSum extends RecursiveTask<Long> {
    // 任务拆分最小阈值
    static final int SEQUENTIAL_THRESHOLD = 10000000;

    // 记录每个任务中元素的起始和终止位置
    // 如果任务中的元素个数超过了拆分的最小阈值就会进一步拆分
    // 直到被拆成最小的任务
    int low;
    int high;
    int[] array;

    LongSum(int[] arr, int lo, int hi) {
        array = arr;
        low = lo;
        high = hi;
    }

    @Override
    protected Long compute() {

        //当任务拆分到小于等于阀值时开始求和
        if (high - low <= SEQUENTIAL_THRESHOLD) {

            long sum = 0;
            for (int i = low; i < high; ++i) {
                sum += array[i];
            }
            return sum;
        } else {  // 任务过大继续拆分
            int mid = low + (high - low) / 2;
            LongSum left = new LongSum(array, low, mid);
            LongSum right = new LongSum(array, mid, high);
            // 提交任务
            left.fork();
            right.fork();
            //获取任务的执行结果return left.join() + right.join();
        }
    }
}