文章目录
一、仿真名称
蛮力法与减治算法应用
二、仿真目的
1.掌握蛮力法和减治法的基本思想;
2.学会运用蛮力法和减治算法解决实际系统设计应用中碰到的问题。
1.基于蛮力法思想实现
1.1、 伪代码描述
算法 solveKs(w,v,index,capacity)
//实现放入背包的物品价值最大化
//输入背包的容量capacity,价值v和质量w.存储了商品质量W[0…n-1]和价值的数组V[0…n-1]
//输出背包的最大价值
v←0,m←0
If index<0 and capacity<0
Return 0
Else
res←solveKs(w,v,index-1,capacity) //不存放第i个物品所得价值
if
w[index]<=capacity
res←Math.max(res,v[index]+solveKs(w,v,index-1,capacity-w[index]//放入或者不放入第i个物品时,背包最大的价值。
Return res
1.2、代码实现
package com.back.cc;
import java.util.Scanner;
public class Test {
public static void main(String[] args) {
int capacity;// 容量
int m;// 数量
int w = 0;// 初始化背包重量
int v = 0;// 初始化背包价值
// 输入背包的容量和商品的数量
System.out.println("请输入商品的数量:");
Scanner sc = new Scanner(System.in);
m = sc.nextInt();// 获得商品数量
System.out.println("请输入背包的容量:");
capacity = sc.nextInt();
// 用数组存储商品的大小和价值
int[] weight = new int[m];
int[] values = new int[m];
// 通过循环赋值
for (int i = 0; i < m; i++) {
System.out.println("请输入第" + (i + 1) + "个商品的质量:");
weight[i] = sc.nextInt();
System.out.println("请输入第" + (i + 1) + "个商品的价值:");
values[i] = sc.nextInt();
}
//直接调用静态方法
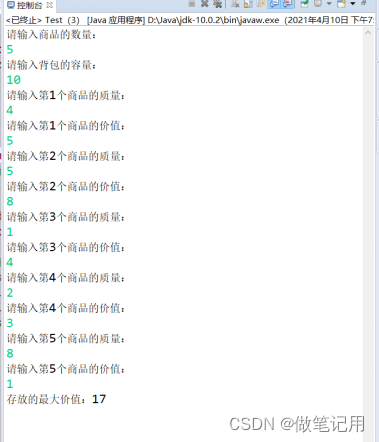
System.out.println("存放的最大价值:"+knapSack(weight, values, capacity));
// long time1 = System.currentTimeMillis();
// long time2 = System.currentTimeMillis();
// int time = (int) ((time2 - time1) / 1000);
// System.out.println("执行了:" + time + "秒!");
}
public static int knapSack(int[] w, int[] v, int C) {
int size = w.length;
return solveKS(w, v, size - 1, C);
}
private static int solveKS(int[] w, int[] v, int index, int capacity) {
// 基准条件:如果索引无效或者容量不足,直接返回当前价值0
if (index < 0 || capacity <= 0)
return 0;
// 不放第index个物品所得价值
int res = solveKS(w, v, index - 1, capacity);
// 放第index个物品所得价值(前提是:第index个物品可以放得下)
if (w[index] <= capacity) {
res = Math.max(res, v[index] + solveKS(w, v, index - 1, capacity - w[index]));
}
return res;
}
}
1.3、背包问题的时间效率分析
将前i件物品放入容量为v的背包中”这个子问题,若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品,那么问题就转化为“前i-1件物品放入容量为v的背包中”,价值为f[i-1][v];如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”,此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。优化空间复杂度以上方法的时间和空间复杂度均为(V N).
2.基于减治法思想实现二叉查找树的插入与查找
2.1 、二叉查找树的插入与查找的伪代码描述
算法:find(v)
//查找二叉树中的数据
//输入数据
//输出:找到数据打印出数据,否则显示无数据
While a!=b do
If a<b c←c.leftchild //如果数据比根节点数据小,则将当前的根节点赋值左孩子
Else c←c.rightchild
Return c
算法:insert(treenode)
//向二叉树插入数据
//输入要插入的值
//输出插入结束后的二叉树
Current ←null ,parent←null a←1
If root==null
Root=newnode
Else
Current=root
While a do
If b<c
current←current.leftchild //当前节点的左孩子赋值给当前节点。当前节点指向左子树
if current==null
parament.leftchild←b //将新节点插入到左子树的空位置
else
current←current.rightchild
if current==null
parament.rightchild←b //将新节点插入到右子树的空位置
2.2、二叉查找树的插入与查找的源代码实现
package com.find.insert;
class TreeNode{
int value;
TreeNode leftChild;
TreeNode rightChild;
public TreeNode() {
}
public TreeNode(int value) {
this.value = value;
leftChild = null;
rightChild = null;
}
public String toString() {
return "Node [value=" + value +"]";
}
}
package com.find.insert;
import java.util.LinkedList;
import java.util.Queue;
class Tree {
TreeNode root = null;
// 查找数据,找到数据打印出该节点
/**
* 查找原理:
* 1、查找的数据和根节点的数值比较。相等返回根节点。
* 2、小于根节点进入左子树查找
* 3、大于根节点进入右子树查找
* 4、左右子树都查找不到返回空值
*
*/
public TreeNode find(int value) {
TreeNode current = root; //把根节点的值赋值给当前指向
while (current.value != value) {
if (value < current.value)
current = current.leftChild;
else
current = current.rightChild;
if (current == null)
System.out.println("当前的二叉树没有此数值!!!");
}
return current;
}
public void insert(TreeNode treenode) {
if (root == null) {
root = treenode;
} else {
TreeNode current = root;
TreeNode parent;
while (true) {
while (true) {
parent = current;//父节点
if (treenode.value < parent.value) {
current = current.leftChild;
if (current == null) {
parent.leftChild = treenode;
return;
}
} else {
current = current.rightChild;
if (current == null) {
parent.rightChild = treenode;
return;
}
}
}
}
}
}
public void levelOrderByStack() {
System.out.println("采用层次遍历二叉树:");
if (root == null)
return;
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.add(root);
while (queue.size() != 0) {
int len = queue.size();
for (int i = 0; i < len; i++) {
TreeNode temp = queue.poll();// 出队列
System.out.print(temp.value + " ");// 输出出队列的值
if (temp.leftChild != null)
queue.add(temp.leftChild);
if (temp.rightChild != null)
queue.add(temp.rightChild);
}
}
}
}
package com.find.insert;
public class TreeDemo {
public static void main(String[] args) {
Tree tree = new Tree();
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(1);
TreeNode node3 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
tree.insert(node1);
tree.insert(node2);
tree.insert(node3);
tree.insert(node4);
tree.insert(node5);
tree.insert(node6);
//查找
System.out.println(tree.find(3));
//层次遍历
tree.levelOrderByStack();
System.out.println();
//插入数据
TreeNode node7 = new TreeNode(7);
tree.insert(node7);
//层次遍历
tree.levelOrderByStack();
}
2.3、叉查找树的插入与查找的时间效率分析
在构建二叉搜索树时,如果插入元素有序或接近有序,如 1 2 3 4 5 6,二叉搜索树退化成为一颗单支树,此时查找的时间复杂度为O(N),此时插入的效率也是O(N);如果左右子树都存在,存在叶子结点,查找的效率和插入的效率是二叉树的高度。
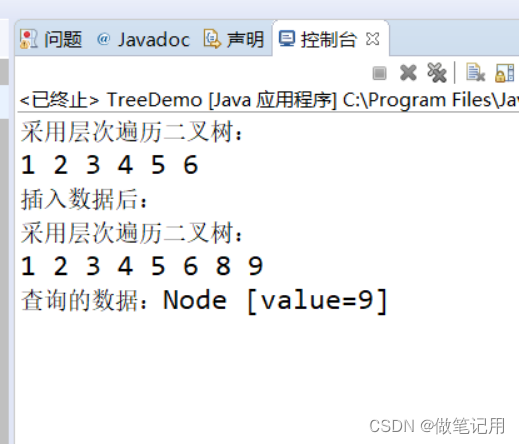
3、测试结果
3.1、基于减治法思想实现二叉查找树的插入与查找的测试用例结果截图