深度学习与计算机视觉系列(3)_线性SVM与SoftMax分类器

深度学习与计算机视觉系列(3)_线性SVM与SoftMax分类器

 

作者： 寒小阳 
时间：2015年11月。 
出处：http://blog.csdn.net/han_xiaoyang/article/details/49999299 
声明：版权所有，转载请注明出处，谢谢。

1. 线性分类器

在深度学习与计算机视觉系列(2)我们提到了图像识别的问题，同时提出了一种简单的解决方法——KNN。然后我们也看到了KNN在解决这个问题的时候，虽然实现起来非常简单，但是有很大的弊端：

• 分类器必须记住全部的训练数据(因为要遍历找近邻啊！！)，而在任何实际的图像训练集上，数据量很可能非常大，那么一次性载入内存，不管是速度还是对硬件的要求，都是一个极大的挑战。
• 分类的时候要遍历所有的训练图片，这是一个相当相当相当耗时的过程。

这个部分我们介绍一类新的分类器方法，而对其的改进和启发也能帮助我们自然而然地过渡到深度学习中的卷积神经网。有两个重要的概念：

• 得分函数/score function：将原始数据映射到每个类的打分的函数
• 损失函数/loss function：用于量化模型预测结果和实际结果之间吻合度的函数

在我们得到损失函数之后，我们就将问题转化成为一个最优化的问题，目标是得到让我们的损失函数取值最小的一组参数。

2. 得分函数/score function

首先我们定义一个有原始的图片像素值映射到最后类目得分的函数，也就是这里提到的得分函数。先笼统解释一下，一会儿我们给个具体的实例来说明。假设我们的训练数据为xi∈RD，对应的标签yi，这里i=1…N表示N个样本，yi∈1…K表示K类图片。

比如CIFAR-10数据集中N=50000，而D=32x32x3=3072像素，K=10，因为这时候我们有10个不同的类别(狗/猫/车…)，我们实际上要定义一个将原始像素映射到得分上函数 f:RD↦RK

2.1 线性分类器

我们先丢出一个简单的线性映射： 

f(xi,W,b)=Wxi+b 

在这个公式里，我们假定图片的像素都平展为[D x 1]的向量。然后我们有两个参数：W是[K x D]的矩阵，而向量b为[K x 1]的。在CIFAR-10中，每张图片平展开得到一个[3072 x 1]的向量，那W就应该是一个[10 x 3072]的矩阵，b为[10 x 1]的向量。

 

这样，以我们的线性代数知识，我们知道这个函数，接受3072个数作为输入，同时输出10个数作为类目得分。我们把W叫做权重，b叫做偏移向量。

说明几个点：

• 我们知道一次矩阵运算，我们就可以借助W把原始数据映射为10个类别的得分。
• 其实我们的输入(xi,yi)其实是固定的，我们现在要做的事情是，我们要调整W, b使得我们的得分结果和实际的类目结果最为吻合。
• 我们可以想象到，这样一种分类解决方案的优势是，一旦我们找到合适的参数，那么我们最后的模型可以简化到只有保留W, b即可，而所有原始的训练数据我们都可以不管了。
• 识别阶段，我们需要做的事情仅仅是一次矩阵乘法和一次加法，这个计算量相对之前…不要小太多好么…

提前剧透一下，其实卷积神经网做的事情也是类似的，将原始输入的像素映射成类目得分，只不过它的中间映射更加复杂，参数更多而已…

2.2 理解线性分类器

我们想想，其实线性分类器在做的事情，是对每个像素点的三个颜色通道，做计算。咱们拟人化一下，帮助我们理解，可以认为设定的参数/权重不同会影响分类器的『性格』，从而使得分类器对特定位置的颜色会有自己的喜好。

举个例子，假如说我们的分类器要识别『船只』，那么它可能会喜欢图片的四周都是蓝色(通常船只是在水里海里吧…)。

我们用一个实际的例子来表示这个得分映射的过程，大概就是下图这个样子：

原始像素点向量xi经过W和b映射为对应结果类别的得分f(xi,W,b)=Wxi+b。不过上面这组参数其实给的是不太恰当的，因为我们看到在这组参数下，图片属于狗狗的得分最高 -_-||

2.2.1 划分的第1种理解

图片被平展开之后，向量维度很高，高维空间比较难想象。我们简化一下，假如把图片像素输入，看做可以压缩到二维空间之中的点，那我们想想，分类器实际上在做的事情就如下图所示：

W中的每一列对应类别中的每一类，而当我们改变W中的值的时候，图上的线的方向会跟着改变，那么b呢？对，b是一个偏移量，它表示当我们的直线方向确定以后，我们可以适当平移直线到合适的位置。没有b会怎么样呢，如果直线没有偏移量，那意味着所有的直线都要通过原点，这种强限制条件下显然不能保证很好的平面类别分割。

2.2.2 划分的第2种理解

对W第二种理解方式是，W的每一行可以看做是其中一个类别的模板。而我们输入图片相对这个类别的得分，实际上是像素点和模板匹配度(通过内积运算获得)，而类目识别实际上就是在匹配图像和所有类别的模板，找到匹配度最高的那个。

是不是感觉和KNN有点类似的意思？是有那么点相近，但是这里我们不再比对所有图片，而是比对类别的模板，这样比对次数只和类目数K有关系，所以自然计算量要小很多,同时比对的时候用的不再是l1或者l2距离，而是内积计算。

我们提前透露一下CIFAR-10上学习到的模板的样子：

你看，和我们设想的很接近，ship类别的周边有大量的蓝色，而car的旁边是土地的颜色。

2.2.3 关于偏移量的处理

我们先回到如下的公式： 

f(xi,W,b)=Wxi+b 

公式中有W和b两个参数，我们知道调节两个参数总归比调节一个参数要麻烦，所以我们用一点小技巧，来把他们组合在一起，放到一个参数中。

 

我们现在要做的运算是矩阵乘法再加偏移量，最常用的合并方法就是，想办法把b合并成W的一部分。我们仔细看看下面这张图片：

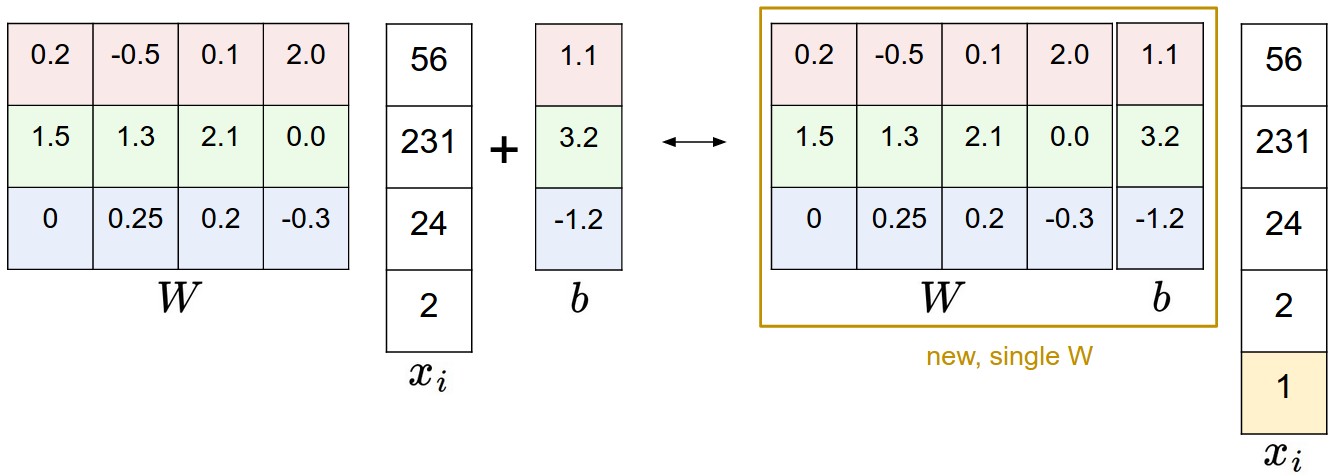
我们给输入的像素矩阵加上一个1，从而把b拼接到W里变成一个变量。依旧拿CIFAR-10举例，原本是[3072 x 1]的像素向量，我们添上最后那个1变成[3073 x 1]的向量，而[W]变成[W b]。

2.2.4 关于数据的预处理

插播一段，实际应用中，我们很多时候并不是把原始的像素矩阵作为输入，而是会预先做一些处理，比如说，有一个很重要的处理叫做『去均值』，他做的事情是对于训练集，我们求得所有图片像素矩阵的均值，作为中心，然后输入的图片先减掉这个均值，再做后续的操作。有时候我们甚至要对图片的幅度归一化/scaling。去均值是一个非常重要的步骤，原因我们在后续的梯度下降里会提到。

2.3 损失函数

我们已经通过参数W，完成了由像素映射到类目得分的过程。同时，我们知道我们的训练数据(xi,yi)是给定的，我们可以调整的是参数/权重W，使得这个映射的结果和实际类别是吻合的。

我们回到最上面的图片中预测 [猫/狗/船] 得分的例子里，这个图片中给定的W显然不是一个合理的值，预测的结果和实际情况有很大的偏差。于是我们现在要想办法，去把这个偏差表示出来，拟人一点说，就是我们希望我们的模型在训练的过程中，能够对输出的结果计算并知道自己做的好坏。

而能帮助我们完成这件事情的工具叫做『损失函数/loss function』，其实它还有很多其他的名字，比如说，你说不定在其他的地方听人把它叫做『代价函数/cost function』或者『客观度/objective』，直观一点说，就是我们输出的结果和实际情况偏差很大的时候，损失/代价就会很大。

2.3.1 多类别支持向量机损失/Multiclass Support Vector Machine loss

腻害的大神们定义出了好些损失函数，我们这里首先要介绍一种极其常用的，叫做多类别支持向量机损失(Multiclass SVM loss)。如果要用一句精简的话来描述它，就是它(SVM)希望正确的类别结果获得的得分比不正确的类别，至少要高上一个固定的大小Δ。

我们先解释一下这句话，一会儿再举个例子说明一下。对于训练集中的第i张图片数据xi，我们的得分函数，在参数W下会计算出一个所有类得分结果f(xi,W)，其中第j类得分我们记作f(xi,W)j，该图片的实际类别为yi，则对于第i张样本图片，我们的损失函数是如下定义的：

 

Li=∑j≠yimax(0,f(xi,W)j−f(xi,W)yi+Δ) 

 

看公式容易看瞎，译者也经常深深地为自己智商感到捉急，我们举个例子来解释一下这个公式。 
假如我们现在有三个类别，而得分函数计算某张图片的得分为f(xi,W)=[13,−7,11]，而实际的结果是第一类(yi=0)。假设Δ=10(这个参数一会儿会介绍)。上面的公式把错误类别(j≠yi)都遍历了一遍，求值加和： 

Li=max(0,−7−13+10)+max(0,11−13+10)

 

仔细看看上述的两项，左边项-10和0中的最大值为0，因此取值是零。其实这里的含义是，实际的类别得分13要比第二类得分-7高出20，超过了我们设定的正确类目和错误类目之间的最小margin Δ=10，因此第二类的结果我们认为是满意的，并不带来loss，所以值为0。而第三类得分11，仅比13小2，没有大于Δ=10，因此我们认为他是有损失/loss的，而损失就是当前距离2距离设定的最小距离Δ的差距8。

注意到我们的得分函数是输入像素值的一个线性函数(f(xi;W)=Wxi)，因此公式又可以简化为(其中wj是W的第j行)： 

Li=∑j≠yimax(0,wTjxi−wTyixi+Δ) 

 

我们还需要提一下的是，关于损失函数中max(0,-)的这种形式，我们也把它叫做hinge loss/铰链型损失，有时候你会看到squared hinge loss SVM(也叫L2-SVM)，它用到的是max(0,−)2，这个损失函数惩罚那些在设定Δ距离之内的错误类别的惩罚度更高。两种损失函数标准在特定的场景下效果各有优劣，要判定用哪个，还是得借助于交叉验证/cross-validation。

对于损失函数的理解，可以参照下图： 

 

 

2.3.2 正则化

如果大家仔细想想，会发现，使用上述的loss function，会有一个bug。如果参数W能够正确地识别训练集中所有的图片(损失函数为0)。那么我们对M做一些变换，可以得到无数组也能满足loss function=0的参数W’(举个例子，对于λ>1的所有λW，原来的错误类别和正确类别之间的距离已经大于Δ，现在乘以λ，更大了，显然也能满足loss为0)。

于是…我们得想办法把W参数的这种不确定性去除掉啊…这就是我们要提到的正则化，我们需要在原来的损失函数上再加上一项正则化项(regularization penalty R(W))，最常见的正则化项是L2范数，它会对幅度很大的特征权重给很高的惩罚： 

R(W)=∑k∑lW2k,l 

根据公式可以看到，这个表达式R(W)把所有W的元素的平方项求和了。而且它和数据本身无关，只和特征权重有关系。

 

我们把两部分组(数据损失/data loss和正则化损失/regularization loss)在一起，得到完整的多类别SVM损失权重，如下： 

L=1N∑iLidata loss+λR(W)⏟regularization loss 

 

也可以展开，得到更具体的完整形式： 

L=1N∑i∑j≠yi[max(0,f(xi;W)j−f(xi;W)yi+Δ)]+λ∑k∑lW2k,l 

 

其中N是训练样本数，我们给正则化项一个参数λ，但是这个参数的设定只有通过实验确定，对…还是得交叉验证/cross-validation。

关于设定这样一个正则化惩罚项为什么能解决W的不确定性，我们在之后的系列里会提到，这里我们举个例子简单看看，这个项是怎么起到作用的。

假定我们的输入图片像素矩阵是x=[1,1,1,1]，而现在我们有两组不同的W权重参数中对应的向量w1=[1,0,0,0]，w2=[0.25,0.25,0.25,0.25]。那我们很容易知道wT1x=wT2x=1，所以不加正则项的时候，这俩得到的结果是完全一样的，也就意味着——它们是等价的。但是加了正则项之后，我们发现w2总体的损失函数结果更小(因为4*0.25^2<1)，于是我们的系统会选择w2，这也就意味着系统更『喜欢』权重分布均匀的参数，而不是某些特征权重明显高于其他权重(占据绝对主导作用)的参数。

之后的系列里会提到，这样一个平滑的操作，实际上也会提高系统的泛化能力，让其具备更高的通用性，而不至于在训练集上过拟合。

另外，我们在讨论过拟合的这个部分的时候，并没有提到b这个参数，这是因为它并不具备像W一样的控制输入特征的某个维度影响力的能力。还需要说一下的是，因为正则项的引入，训练集上的准确度是会有一定程度的下降的，我们永远也不可能让损失达到零了(因为这意味着正则化项为0，也就是W=0)。

下面是简单的计算损失函数(没加上正则化项)的代码，有未向量化和向量化两种形式：

def L_i(x, y, W):
  """
  未向量化版本. 
  对给定的单个样本(x,y)计算multiclass svm loss.
  - x: 代表图片像素输入的向量 (例如CIFAR-10中是3073 x 1，因为添加了bias项对应的1到x中)
  - y: 图片对应的类别编号(比如CIFAR-10中是0-9)
  - W: 权重矩阵 (例如CIFAR-10中是10 x 3073)
  """
  delta = 1.0 # 设定delta
  scores = W.dot(x) # 内积计算得分
  correct_class_score = scores[y]
  D = W.shape[0] # 类别数:例如10
  loss_i = 0.0
  for j in xrange(D): # 遍历所有错误的类别
    if j == y:
      # 跳过正确类别
      continue
    # 对第i个样本累加loss
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i

def L_i_vectorized(x, y, W):
  """ 
  半向量化的版本，速度更快。
  之所以说是半向量化，是因为这个函数外层要用for循环遍历整个训练集 -_-||
  """ 
  delta = 1.0
  scores = W.dot(x)
  # 矩阵一次性计算
  margins = np.maximum(0, scores - scores[y] + delta)

  margins[y] = 0 
  loss_i = np.sum(margins)
  return loss_i

def L(X, y, W):
  """ 
  全向量化实现 :
  - X: 包含所有训练样本中数据(例如CIFAR-10是3073 x 50000)
  - y: 所有的类别结果 (例如50000 x 1的向量)
  - W: 权重矩阵 (例如10 x 3073)
  """
  #待完成...

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22
• 23
• 24
• 25
• 26
• 27
• 28
• 29
• 30
• 31
• 32
• 33
• 34
• 35
• 36
• 37
• 38
• 39
• 40
• 41
• 42
• 43

说到这里，其实我们的损失函数，是提供给我们一个数值型的表示，来衡量我们的预测结果和实际结果的差别。而要提高预测的准确性，要做的事情是，想办法最小化这个loss。

2.4 一些现实的考虑点

2.4.1 设定Delta

我们在计算Multi SVM loss的时候，Δ是我们提前设定的一个参数。这个值咋设定？莫不是…也需要交叉验证…？其实基本上大部分的场合下我们设定Δ=1.0都是一个安全的设定。我们看公式中的参数Δ和λ似乎是两个截然不同的参数，实际上他俩做的事情比较类似，都是尽量让模型贴近标准预测结果的时候，在 数据损失/data loss和 正则化损失/regularization loss之间做一个交换和平衡。

在损失函数计算公式里，可以看出，权重W的幅度对类别得分有最直接的影响，我们减小W，最后的得分就会减少；我们增大W，最后的得分就增大。从这个角度看，Δ这个参数的设定(Δ=1或者Δ=100)，其实无法限定W的伸缩。而真正可以做到这点的是正则化项，λ的大小，实际上控制着权重可以增长和膨胀的空间。

2.4.2 关于二元/Binary支持向量机

如果大家之前接触过Binary SVM，我们知道它的公式如下： 

Li=Cmax(0,1−yiwTxi)+R(W) 

 

我们可以理解为类别yi∈−1,1，它是我们的多类别识别的一个特殊情况，而这里的C和λ是一样的作用，只不过他们的大小对结果的影响是相反的，也就是C∝1λ

2.4.3 关于非线性的SVM

如果对机器学习有了解，你可能会了解很多其他关于SVM的术语：kernel，dual，SMO算法等等。在这个系列里面我们只讨论最基本的线性形式。当然，其实从本质上来说，这些方法都是类似的。

2.5 Softmax分类器

话说其实有两种特别常见的分类器，前面提的SVM是其中的一种，而另外一种就是Softmax分类器，它有着截然不同的损失函数。如果你听说过『逻辑回归二分类器』，那么Softmax分类器是它泛化到多分类的情形。不像SVM这种直接给类目打分f(xi,W)并作为输出，Softmax分类器从新的角度做了不一样的处理，我们依旧需要将输入的像素向量映射为得分f(x_i; W) = W x_i，只不过我们还需要将得分映射到概率域，我们也不再使用hinge loss了，而是使用交叉熵损失/cross-entropy loss，形式如下： 

Li=−log(efyi∑jefj)或者Li=−fyi+log∑jefj 

 

我们使用fj来代表得分向量f的第j个元素值。和前面提到的一样，总体的损失/loss也是Li遍历训练集之后的均值，再加上正则化项R(W)，而函数fj(z)=ezj∑kezk被称之为softmax函数：它的输入值是一个实数向量z，然后在指数域做了一个归一化(以保证之和为1)映射为概率。

2.5.1 信息论角度的理解

对于两个概率分布p(“真实的概率分布”)和估测的概率分布q(估测的属于每个类的概率)，它们的互熵定义为如下形式： 

H(p,q)=−∑xp(x)logq(x) 

 

而Softmax分类器要做的事情，就是要最小化预测类别的概率分布(之前看到了，是q=efyi/∑jefj)与『实际类别概率分布』(p=[0,…1,…,0]，只在结果类目上是1，其余都为0)两个概率分布的交叉熵。

另外，因为互熵可以用熵加上KL距离/Kullback-Leibler Divergence(也叫相对熵/Relative Entropy)来表示，即H(p,q)=H(p)+DKL(p||q)，而p的熵为0(这是一个确定事件，无随机性)，所以互熵最小化，等同于最小化两个分布之间的KL距离。换句话说，交叉熵想要从给定的分布q上预测结果分布p。

2.5.2 概率角度的理解

我们再来看看以下表达式 

P(yi∣xi;W)=efyi∑jefj 

 

其实可以看做给定图片数据xi和类别yi以及参数W之后的归一化概率。在概率的角度理解，我们在做的事情，就是最小化错误类别的负log似然概率，也可以理解为进行最大似然估计/Maximum Likelihood Estimation (MLE)。这个理解角度还有一个好处，这个时候我们的正则化项R(W)有很好的解释性，可以理解为整个损失函数在权重矩阵W上的一个高斯先验，所以其实这时候是在做一个最大后验估计/Maximum a posteriori (MAP)。

2.5.3 实际工程上的注意点：数据稳定性

在我们要写代码工程实现Softmax函数的时候，计算的中间项efyi和∑jefj因为指数运算可能变得非常大，除法的结果非常不稳定，所以这里需要一个小技巧。注意到，如果我们在分子分母前都乘以常数C，然后整理到指数上，我们会得到下面的公式： 

efyi∑jefj=CefyiC∑jefj=efyi+logC∑jefj+logC 

 

C的取值由我们而定，不影响最后的结果，但是对于实际计算过程中的稳定性有很大的帮助。一个最常见的C取值为logC=−maxjfj。这表明我们应该平移向量f中的值使得最大值为0，以下的代码是它的一个实现：

f = np.array([123, 456, 789]) # 3个类别的预测示例
p = np.exp(f) / np.sum(np.exp(f)) # 直接运算，数值稳定性不太好

# 我们先对数据做一个平移，所以输入的最大值为0:
f -= np.max(f) # f 变成 [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # 结果正确，同时解决数值不稳定问题

• 1
• 2
• 3
• 4
• 5
• 6

• 1
• 2
• 3
• 4
• 5
• 6

2.5.4 关于softmax这个名字的一点说明

准确地说，SVM分类器使用hinge loss(有时候也叫max-margin loss)。而Softmax分类器使用交叉熵损失/cross-entropy loss。Softmax分类器从softmax函数(恩，其实做的事情就是把一列原始的类别得分归一化到一列和为1的正数表示概率)得到，softmax函数使得交叉熵损失可以用起来。而实际上，我们并没有softmax loss这个概念，因为softmax实质上就是一个函数，有时候我们图方便，就随口称呼softmax loss。

2.6 SVM 与 Softmax

这个比较很有意思，就像在用到分类算法的时候，就会想SVM还是logistic regression呢一样。 
我们先用一张图来表示从输入端到分类结果，SVM和Softmax都做了啥： 

 

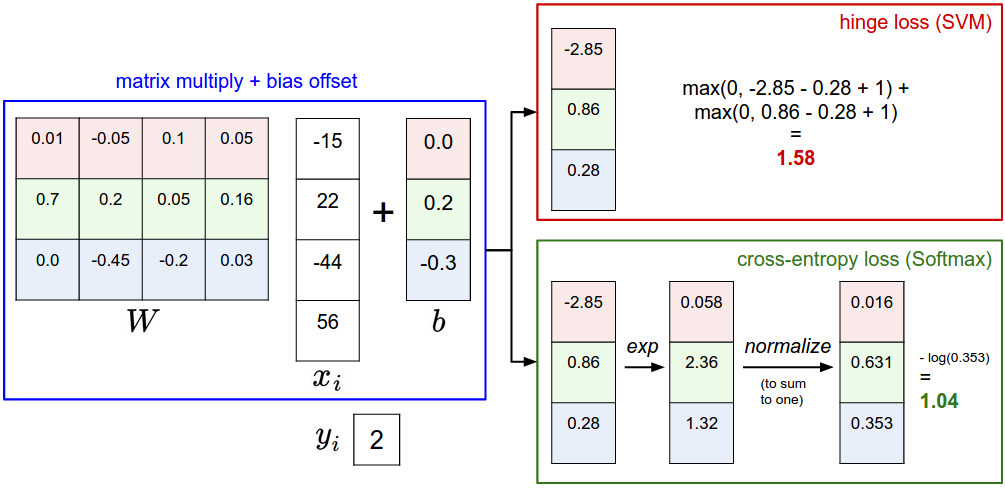
区别就是拿到原始像素数据映射得到的得分之后的处理，而正因为处理方式不同，我们定义不同的损失函数，有不同的优化方法。

2.6.1 另外的差别

• SVM下，我们能完成类别的判定，但是实际上我们得到的类别得分，大小顺序表示着所属类别的排序，但是得分的绝对值大小并没有特别明显的物理含义。
• Softmax分类器中，结果的绝对值大小表征属于该类别的概率。

举个例子说，SVM可能拿到对应 猫/狗/船 的得分[12.5, 0.6, -23.0]，同一个问题，Softmax分类器拿到[0.9, 0.09, 0.01]。这样在SVM结果下我们只知道『猫』是正确答案，而在Softmax分类器的结果中，我们可以知道属于每个类别的概率。

但是，Softmax中拿到的概率，其实和正则化参数λ有很大的关系，因为λ实际上在控制着W的伸缩程度，所以也控制着最后得分的scale，这会直接影响最后概率向量中概率的『分散度』，比如说某个λ下，我们得到的得分和概率可能如下： 

[1,−2,0]→[e1,e−2,e0]=[2.71,0.14,1]→[0.7,0.04,0.26] 

 

而我们加大λ，提高其约束能力后，很可能得分变为原来的一半大小，这时候如下： 

[0.5,−1,0]→[e0.5,e−1,e0]=[1.65,0.37,1]→[0.55,0.12,0.33] 

 

因为λ的不同，使得最后得到的结果概率分散度有很大的差别。在上面的结果中，猫有着统治性的概率大小，而在下面的结果中，它和船只的概率差距被缩小。

2.6.2 际应用中的SVM与Softmax分类器

实际应用中，两类分类器的表现是相当的。当然，每个人都有自己的喜好和倾向性，习惯用某类分类器。

一定要对比一下的话：

SVM其实并不在乎每个类别得到的绝对得分大小，举个例子说，我们现在对三个类别，算得的得分是[10, -2, 3]，实际第一类是正确结果，而设定Δ=1，那么10-3=7已经比1要大很多了，那对SVM而言，它觉得这已经是一个很标准的答案了，完全满足要求了，不需要再做其他事情了，结果是 [10, -100, -100] 或者 [10, 9, 9]，它都是满意的。

然而对于Softmax而言，不是这样的， [10, -100, -100] 和 [10, 9, 9]映射到概率域，计算得到的交叉熵损失是有很大差别的。所以Softmax是一个永远不会满足的分类器，在每个得分计算到的概率基础上，它总是觉得可以让概率分布更接近标准结果一些，交叉熵损失更小一些。

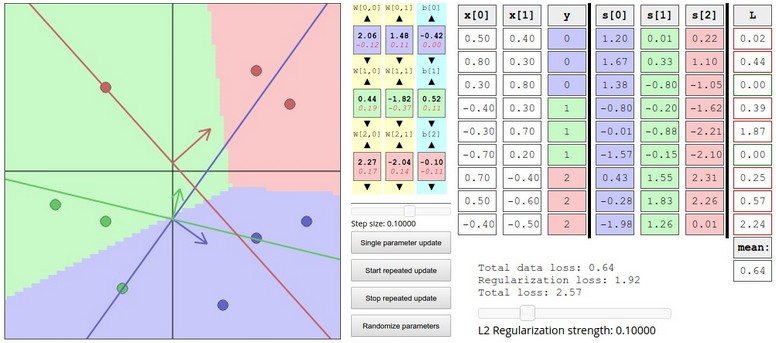
有兴趣的话，W与得分预测结果demo是一个可以手动调整和观察二维数据上的分类问题，随W变化结果变化的demo，可以动手调调看看。 

 

 

参考资料与原文

cs231n 线性分类器 SVM与softmax