[LeetCode 84.] 柱状图中最大的矩形
LeetCode 84. 柱状图中最大的矩形
题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
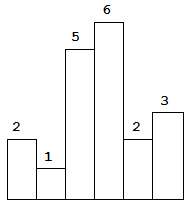
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。

图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10
解题思路
这道题看起来没有接雨水的实际应用场景那么强,唯一的应用例子是楼房安装广告牌。
最直观的解题思路依旧是暴力解法,遍历没一个柱子,然后左右拓展,直到小于当前柱子高度。暴力解法的时间复杂度是O(N^2)。
不同于接雨水,这道题没有很好的通过记录“状态”来压缩实践复杂度的方法。
单调栈
解决办法是单调栈。入栈 —— 保存状态;出栈 —— 计算收益。
与接雨水相比,不同点在于出入栈的触发条件上:
- 接雨水是新条形更高,会触发水位上涨,因而出栈。导致保存状态的单调栈是单调递减的。
- 最大矩形是新条形更低,会阻断矩形扩展,因而出栈。导致保存状态的单调栈是单调递增的。
相同之处在于,二者触发条件时,会从栈顶一直向前触发,直到不满足触发条件为止,从而维护了栈的单调性质。
参考代码
/*
* @lc app=leetcode id=84 lang=cpp
*
* [84] Largest Rectangle in Histogram
*/
// @lc code=start
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int res = 0;
heights.push_back(0); // 插入哨兵,用于最后清空队列
deque<int> q;
for (int i=0; i<heights.size(); i++) {
while (!q.empty() && heights[i] < heights[q.back()]) {
// res = std::max(res, (i-q.back())*heights[q.back()]);
// q.pop_back();
int h = heights[q.back()];
q.pop_back();
int w = q.empty() ? i : (i - q.back() - 1);
res = std::max(res, w * h);
}
q.push_back(i);
}
return res;
}
};
// @lc code=end



