赫夫曼树(最优二叉树)
—— 赫夫曼树 相关概念 ——
结点的权:树中结点被赋予一个表示某种意义的数值,称为该结点的权。
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度(WPL):树中所有叶子结点的带权路径长度之和。
赫夫曼树:当用 n 个结点(都做叶子结点且都有各自的权值)构建一棵树时,如果构建的这棵树的带权路径长度(WPL)最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
例如,下面有3棵二叉树都有4个叶子结点a、b、c、d,分别带权7、5、2、4。
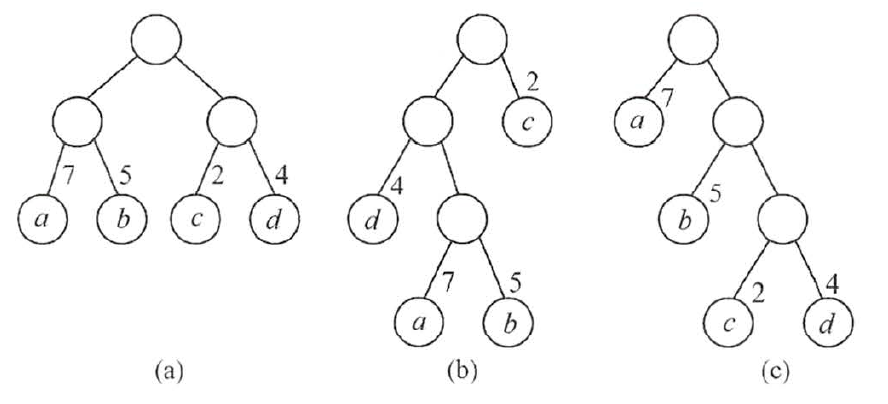
图1 具有不同带权长度的二叉树
它们的带权路径长度分别为:
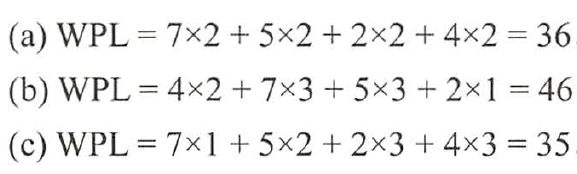
其中,图(c)树的WPL 最小。可以验证,它恰好为赫夫曼树。
在构建赫夫曼树时,要使WPL最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在图 1 中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
一个规律:WPL = 赫夫曼树中所有非叶子结点权值之和。
—— 赫夫曼树的构造 ——
给定n 个权值分别为W 1 ,W 2 ,… , Wn 的结点,构造赫夫曼树的算法描述如下:
- 1)将这n 个结点分别作为n棵仅含一个结点的二叉树,构成森林F。
- 2 )构造一个新结点,从F中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值设置为左、右子树上根结点的权值之和。
- 3 )从F 中删除刚才选出的两棵树,同时将新得到的树加入F 中。
- 4 )重复步骤2)和3), 直至F中只剩下一棵树为止。
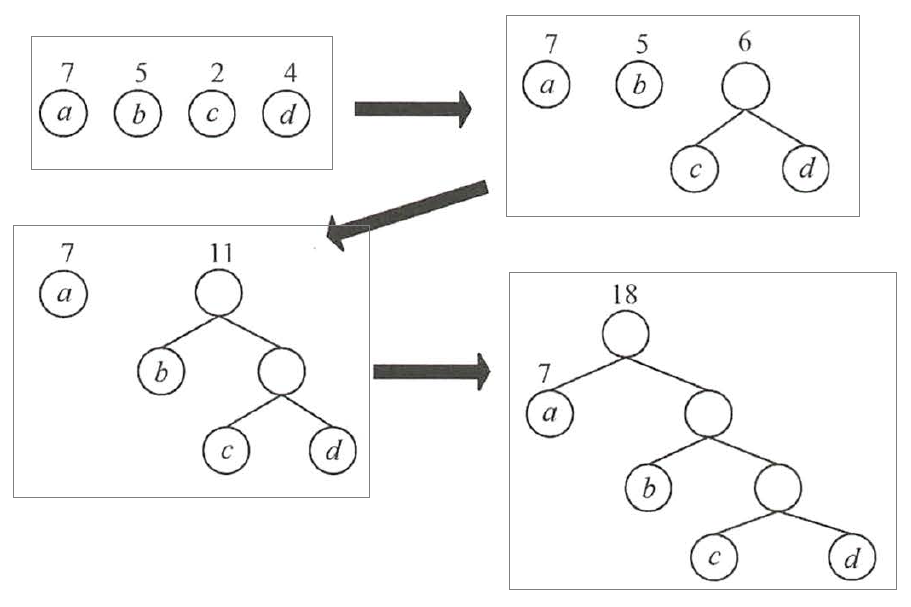
图2 赫夫曼树的构造过程
从上述构造过程中可以看出赫夫曼树具有如下特点:
- 1 )每个初始结点最终都成为叶结点, 且,权值越小的结点到根结点的路径长度越大。
- 2 )构造过程中共新建了n -1个结点(双分支结点),因此ll合夫曼树的结点总数为2n -1 。
- 3 ) 每次构造都选择2 棵树作为新结点的孩子,因此哈夫曼树中不存在度为1的结点。
—— 赫夫曼编码 ——
在数据通信中,若对每个字符用相等长度的二进制位表示,称这种编码方式为固定长度编码。若允许对不同字符用不等长的二进制位表示,则这种编码方式称为可变长度编码。可变长度编码比固定氏度编码要好得多, 其特点是对频率高的字符赋以短编码,而对频率较低的字符则赋以较长一些的编码,从而可以使字符的平均编码长度减短,起到压缩数据的效果。赫夫曼编码是一种被广泛应用而且非常有效的数据压缩编码。
若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码。举例:设计字符A、B和C 对应的编码0、 101 和100 是前缀编码。对前缀编码的解码很简单,因为没有一个编码是其他编码的前缀。所以识别出第一个编码,将它翻译为原码, 再对余下的编码文件重复同样的解码操作。例如,码串00101100 可被唯一地翻译为0, 0, 101 和100 。另举反例:如果再将字符D 的编码设计为00 , 此时0 是00 的前缀,那么这样的码串的前两位就无法唯一翻译。
由赫夫曼树得到赫夫曼编码是很自然的过程。首先,将每个出现的字符当作一个独立的结点,其权值为它出现的频度(或次数),构造出对应的哈夫曼树。显然,所有宇符结点都出现在叶结点中。我们可将字符的编码解释为从根至该字符的路径上边标记的序列,其中边标记为0表示“转向左孩子”,标记为l1表示“转向右孩子”。图3 所示为一个由赫夫曼树构造哈夫曼编码的示例,矩形方块表示字符及其出现的次数。
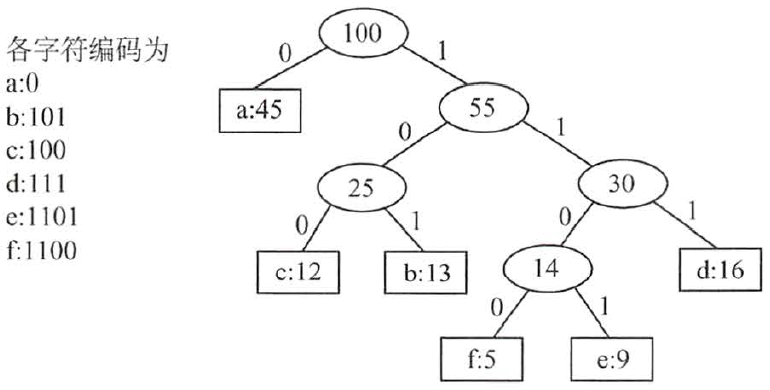
图3 由赫夫曼树构造赫夫曼编码
这棵哈夫曼树的WPL为:
![]()
此处的WPL 可视为最终编码得到二进制编码的长度, 共224 位。若采用3 位固定长度编码,则得到的二进制编码氏度为300 位,因此哈夫曼编码共压缩了25% 的数据。利用哈夫曼树可以设计出总氏度最短的二进制前缀编码。
注意: 0 和1究竟是表示左子树还是右子树没有明确规定。左、右孩子结点的顺序是任意的,所以构造出的赫夫曼树并不唯一,但各赫夫曼树的带权路径长度WPL 相同且为最优。此外, 如有若干权值相同的结点,则构造出的赫夫曼树更可能不同, 但 WPL 必然相同且是最优的。
—— 赫夫曼树的算法实现 ——
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<queue> 5 #include<algorithm> 6 using namespace std; 7 8 //定义结点结构体 9 struct node { 10 int w,h; //w为权重,h为高度, n为结点编号 11 node() {w = 0, h=0;} 12 node(int w, int h): w(w), h(h){} 13 bool operator <(const node &a)const{ //重载运算符 14 return a.w == w ? h>a.h : w>a.w; //优先考虑权值,其次考虑高度 15 } 16 }; 17 18 int wpl; // 赫夫曼树的带权路径长度(WPL) = 赫夫曼树中所有非叶子结点权值之和 19 20 priority_queue<node>q; //类型为node的优先队列 21 22 int main() { 23 24 int w[5] = { 2, 8, 7, 6, 5 }; 25 for(int i = 0; i < 5; i++) { 26 q.push(node(w[i], 1)); //默认h=1, 这里进行强制类型转换 27 } 28 29 /* 构造赫夫曼树,结点两两合并 */ 30 while(q.size() != 1) { 31 int h = 0; 32 int w = 0; 33 34 /* 2个最小的结点作为孩子结点,构造一颗子树 */ 35 node t1 = q.top(); //最小的结点 36 q.pop(); 37 node t2 = q.top(); //次小的结点 38 q.pop(); 39 h = max(t1.h, t2.h); // 2个孩子结点中最大的高度 40 w = t1.w + t2.w; //权值相加 41 42 wpl += w; //wpl 43 q.push(node(w, h + 1)); //父结点进入优先队列,父节点高度在子结点的基础上+1 44 } 45 46 cout<<"WPL = "<<wpl<<endl; 47 48 49 system("pause"); 50 return 0; 51 }
—— K阶 赫夫曼树 ——
对于k叉赫夫曼树的求解,直观的想法是在贪心的基础上,改为每次从堆中去除最小的k个权值合并。我们便可以按照赫夫曼树的构造方式,将当前最小的K个节点合并为1个父节点(显然,可以使用优先队列(二叉堆)进行维护),直至只有一个父节点。
注意一个细节,如果在执行最后一次循环时,堆的大小在(2~k-1)之间(不足以取出k个),那么整个赫夫曼树的根的子节点个数就小于k,也就表明了最靠近根节点的位置反而没有被排满,这显然不是最优解 。因此,我们应该在执行上述贪心算法之前,补加一些额外的权值为0的叶子节点,使叶子节点的个树满足(n-1)%(k-1)=0。
1 // K阶的赫夫曼树 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<queue> 6 #include<algorithm> 7 //#define ll long long 8 using namespace std; 9 10 //定义结点结构体 11 struct node { 12 int w,h; //w为权重,h为高度 13 node() {w = 0, h=0;} 14 node(int w, int h): w(w), h(h) {} 15 bool operator <(const node &a)const{ //重载运算符 16 return a.w == w ? h>a.h : w>a.w; //优先考虑权值,其次考虑高度 17 } 18 }; 19 20 int wpl; 21 22 priority_queue<node>q; //类型为node的优先队列 23 24 int main() { 25 int n,k; 26 cin>>n>>k; 27 for(int i = 1; i <= n; i++) { 28 int w; 29 cin>>w; 30 q.push(node(w,1)); //默认h=1,这里进行强制类型转换 31 } 32 while((q.size()-1) % (k-1) !=0 ) { //需要添加空节点的情况 33 q.push(node(0,1)); //空节点默认w=0,h=1 34 } 35 while(q.size()>=1) { 36 int h = -1; 37 int w = 0; 38 for(int i = 1; i <= k; ++i) { //每次选出最小的k个结点 39 node t = q.top(); 40 q.pop(); 41 h = max(h,t.h); 42 w += t.w; 43 } 44 wpl += w; 45 q.push(node(w, h + 1)); 46 } 47 48 cout<<wpl<<endl; 59 50 system("pause"); 51 return 0; 52 }

