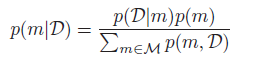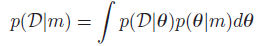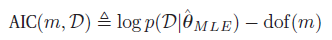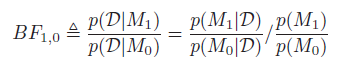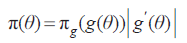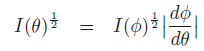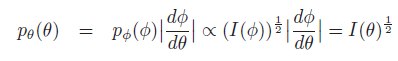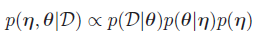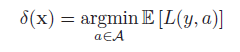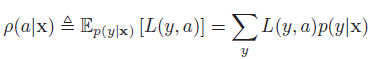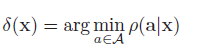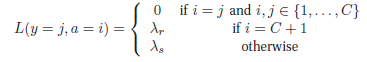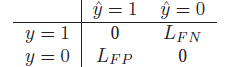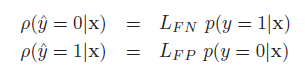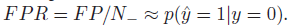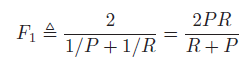Bayesian statistics
文件夹
1Bayesian model selection(贝叶斯模型选择)
使用多项式阶数过高会导致过拟合。过低会导致欠拟合。
正则化參数过小会导致过拟合,过大会导致欠拟合。我们面临一系列不同复杂度的模型,怎样选择,就是模型选择问题。
一个方法是使用交叉验证(cross-validation)来预计全部备选模型的错误。挑选最好的一个模型。However, this requires fitting each model K times, where K is the number of CV folds.
一个高效的方法是计算模型的后验:
我们非常easy计算最大后验概率模型:
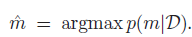
这就叫贝叶斯模型选择。
这个quantity叫marginal likelihood,integrated likelihood,或者模型m的evidence。
1.1奥卡姆剃刀(Occam’s razor)原理
One might think that using p(D|m) to select models would always favor the model with the most parameters. This is true if we use
【在全部可能选择的模型中,能够非常好地解释已知数据而且十分简单才是最好的模型。也就是应该选择的模型。】
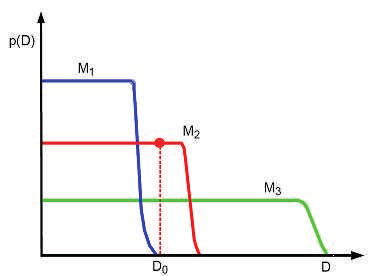
Bayesian Occam’s razor解释图:D0为真实的观測数据,模型M1最简单。M3最复杂。
因为简单的模型仅仅能产生简单的数据,复杂的模型參数多,不仅能够产生简单的数据。同一时候能够产生复杂的数据。当给定的一个数据集后,简单的模型因为表现能力差。使用边缘似然函数比較小。同一时候因为过于复杂的模型能够产生很多其它的复杂数据,那么它产生该特定数据的概率就会相对变小,因此它的边缘似然函数同样不大。仅仅有复杂度适中的模型的边缘似然函数最大。
【如果有K个模型
这个过程叫做模型选择或模型评估。
】
2Computing the marginal likelihood (evidence)
贝叶斯判断中边际似然函数涉及到维数较高的复杂积分的计算, 因而精确地计算边际似然函数往往有困难.常常会选择一种近似方法来预计边际似然函数。
2-1 BIC approximation to log marginal likelihood
一个简单流行的近似是贝叶斯信息标准(Bayesian information criterion or BIC),它的形式为:
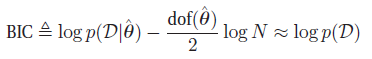
当中, 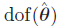
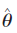
一个非常类似的表达是Akaike information criterion or AIC,定义为
这是来源于频率学框架的。不能用来做marginal likelihood的近似判断。
BIC对參数添加的惩处力度大于户AIC,这使得AIC选择的是更复杂的模型,可是这能导致更好的预測准确性。
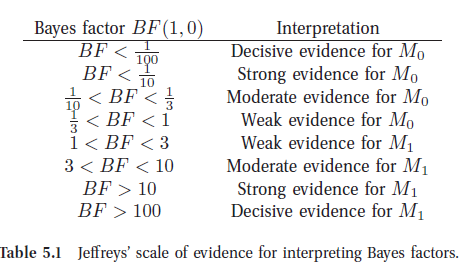
2-2贝叶斯因子
Suppose our prior on models is uniform
考虑模型M0,M1,定义贝叶斯因子为两个的比:
Jeffreys解释贝叶斯因子的标准
3先验
在Bayes 分析中,进行统计判断与决策所依赖的后验分布是以先验分布为基础。因此,怎样获得先验分布是Bayes 方法的最关键问题。
3-1 确定无信息先验分布的Jeffreys原则
Jeffreys先验(Jeffreys’ Prior) Jeffreys提出的选取先验分布的原则是一种不变原理,採用Fisher信息阵的平方根作为θ的无信息先验分布。
Jeffreys 提出了一种基于信息函数的无信息先验分布选择方法,即Jeffreys 原则。较好地攻克了Bayes如果中的一个矛盾,即若对參数θ 选用均匀分布,则其函数g(θ) 往往不是均匀分布。同一时候,该原则给出了寻求先验分布的详细办法。
Jeffreys原则:
依照原则决定參数θ 的先验分布为π(θ) ,对于θ 的函数g(θ) 作为參数,依照同一原则决定的η = g(θ) 的先验分布是πg(η) 。则应有关系式:
若选取的π(θ) 符合上式。则用θ 或θ 的函数g(θ) 导出的先验分布总是一致的。
困难之处在于怎样找出满足上式的π(θ) 。Jeffreys 巧妙的利用了Fisher信息阵的性质。找到了符合要求的π(θ) 。
引理: 设g(θ) 是θ 的函数,η = g(θ) 与θ 具有同样的维数k ,则有:
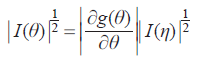
当中。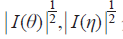
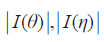
由此引理与Jeffreys原则,可取:π(θ)∝|I(θ)|^{1/2}
该式对标量參数和矢量參数都适用。
推导:
p(φ) is non-informative,θ = h(φ) for some function h, should also be non-informative
let us pick: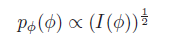
where I(φ) is the Fisher information:
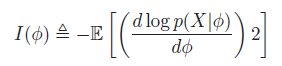
有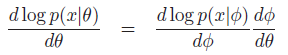
平方并取x的期望,得到
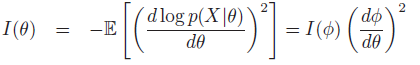
即
so we find the transformed prior is:
So
3-2共轭先验(Conjugate Priors)
共轭先验是指先验分布和后验分布来自同一个分布族的情况。就是说先验和后验有同样的分布形式(当然。參数是不同的)。这些共轭先验是结合似然的形式推导出来的。
Conjugate prior的意义:
使得贝叶斯推理更加方便,比方在Sequential Bayesian inference(连续贝叶斯推理)中。得到一个observation之后。能够算出一个posterior(后验)。因为选取的是 Conjugate prior共轭先验。因此后验和原来先验的形式一样。能够把该后验当做新的先验,用于下一次observation,然后继续迭代。
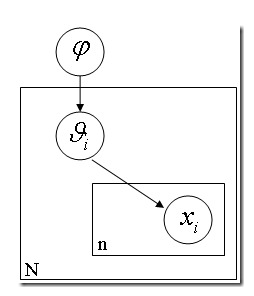
4Hierarchical Bayes
计算后验p(θ|D)的一个关键是带超參数η的p(θ|η),如果我们不知道η,能够使用前面的无信息先验,很多其它的贝叶斯方法是通过先验的先验!
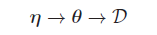
这就是层级贝叶斯模型。
如果你手头有 N 枚硬币。它们是同一个工厂铸出来的。你把每一枚硬币掷出一个结果,然后基于这 N 个结果对这 N 个硬币的 θ (出现正面的比例)进行推理。然而我们又知道每一个硬币的 p(θ) 是有一个先验概率的。或许是一个 beta 分布。也就是说,每一个硬币的实际投掷结果 Xi 服从以 θ 为中心的正态分布,而 θ 又服从还有一个以 Ψ 为中心的 beta 分布。层层因果关系就体现出来了。进而 Ψ 还可能依赖于因果链上更上层的因素。以此类推。
5Empirical Bayes
在分层贝叶斯模型中。我们须要在多层级潜在变量上计算后验。比如。两个层级的模型:
一种经验贝叶斯分析就是用边际分布来预计η,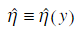
边际极大似然预计。然后以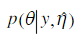
6Bayesian decision theory
选择未知的状态/參数/标签,y ∈ Y,然后产生一个观測x ∈ X。然后我们做出决策。选择一个行为a。从行为空间A中选择。损失为L(y, a)。
比如,使用误分类损失L(y, a) = I(y ≠ a),或者平方损失
我们的目标是产生一个决策过程或者策略,δ : X → A,表示每一个可能的输入最佳的行为action。
最优化,意味着最小化期望损失:
使用贝叶斯方法的决策理论。最优化行为。用于观測x,行为a,最小化后验期望损失:
因此,贝叶斯预计。也称为贝叶斯决策规则(Bayes decision rule)为:
基于最小错误率的贝叶斯决策
以后验概率值的大小做判据
基于最小风险的贝叶斯决策
判决根据为对该观測值X条件下各个状态后验概率求加权和的方法
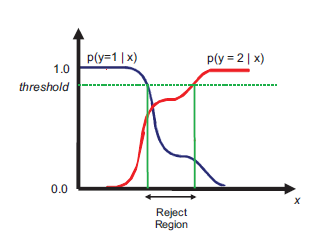
6-1拒绝选择
如上图。分类错误来自于在输入中不同类别在同样空间区域上有重叠,这时候能够採取拒绝分类的方法。即reject option。当样本落在这个区域的时候。就有疑惑的结果留待人类专家来判定。
引入一个阈值threshold,将最大后验概率小于或者等于该阈值的输入样本X拒绝预測。
设a = C + 1相当于选择reject action,a ∈ {1, … , C}相当于选择一个类
定义损失函数为:
λr is the cost of the reject action, and λs is the cost of a substitution error
6-2The false positive vs false negative tradeoff
二元决策问题中两类错误:
1)False Positive 假阳性也被称为误报或者虚警(把“不是”说成“是”),预计量
2)False Negative 假阴性也被称为漏报(把“是”说成“不是”),预计量
损失矩阵:
LFN是false negative的损失。LFP是false positive的损失,则这两个actions的后验期望损失为:
6-2-1完美的ROC曲线
如果类标签数据集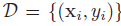

confusion matrix,N+ 是真实数量的阳性, (N_+ ) ̂ 是被声称的阳性, N- 真实数量的阴性,(N_- ) ̂是被声称的阴性。
TPR(true positive rate)
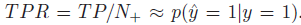
FPR(false alarm rate)
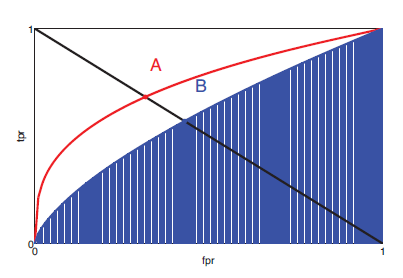
不单单使用一个固定的阈值τ,而是一系列的τ值时,绘制出将FPR定义为x轴,TPR定义为y轴的曲线,称为ROC曲线:
两个如果的分类系统ROC曲线。A比B效果好。
左下角:(FPR = 0, TPR = 0),设置τ=1,全部的类别被分为negative
右上角:(FPR = 1, TPR = 1),设置τ=0。全部的类别被分位positive
【最好的预測方式是一个在左上角的点,在ROC空间坐标轴(0,1)点。这个代表着100%灵敏(没有假阴性)和100%特异(没有假阳性)。而(0,1)点被称为“完美分类器”。
一个全然随机的预測会得到一条从左下到右上对角线(也叫无识别率线)上的一个点,这条线上的任一点相应的精确度(ACC)都是50%。
】
ROC曲线以下的区域称为AUC,AUC分数越高越好。最大为1.
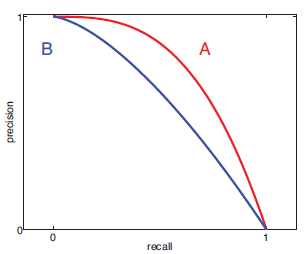
6-2-2Precision Recall曲线(查准率-查全率曲线)
PR曲线在分类、检索等领域有着广泛的使用。来表现分类/检索的性能。
精度:
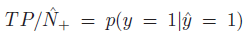
召回率:
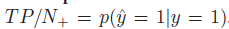
【如果是分类器的话,通过调整分类阈值,能够得到不同的P-R值。从而能够得到一条曲线(纵坐标为P,横坐标为R)。通常随着分类阈值从大到小变化(大于阈值觉得P)。查准率减小,查全率添加。比較两个分类器好坏时。显然是查得又准又全的比較好,也就是的PR曲线越往坐标(1。1)的位置靠近越好。】
precision-recall曲线。A比B效果好。
6-2-3F-scores
在检索系统中。希望检索的结果P越高越好,R也越高越好,但其实这两者在某些情况下是矛盾的。一个综合评价指标定义为F score 或者F1 score:
參考链接:
贝叶斯统计基础