作者：zhbzz2007 出处：http://www.cnblogs.com/zhbzz2007 欢迎转载，也请保留这段声明。谢谢！
这是RNN教程的第三部分。
在前面的教程中，我们从头实现了一个循环神经网络，但是并没有涉及随时间反向传播（BPTT）算法如何计算梯度的细节。在这部分，我们将会简要介绍BPTT并解释它和传统的反向传播有何区别。我们也会尝试着理解梯度消失问题，这也是LSTM和GRU（目前NLP及其它领域中最为流行和有用的模型）得以发展的原因。梯度消失问题最早是由 Sepp Hochreiter 在1991年发现，最近由于深度框架的广泛应用再次获得很多关注。
为了能够完全理解这部分，我建议你熟悉偏微分和基本的反向传播工作原理。如果你不熟悉这些内容，你需要看这些教程 CS231n Convolutional Neural Networks for Visual Recognition 、 Calculus on Computational Graphs: Backpropagation 、 How the backpropagation algorithm works ，这些教程的难度依次增加 。
1 BPTT
让我们快速回忆一下循环神经网络中的一些基本公式。定义中略微有些变化，我们将 \(o\) 修改为 \(\hat{y}\) 。这是为了与一些参考文献保持一致。
\(s_{t} = tanh(U x_{t} + W s_{t-1})\)
\(\hat{y_{t}} = softmax(V s_{t})\)
我们定义损失或者误差为互熵损失，如下所示，
\(E_{t}(y_{t},\hat{y_{t}}) = -y_{t}log(\hat{y_{t}})\)
\(E_{t}(y,\hat{y}) = \sum_{t}E_{t}(y_{t},\hat{y_{t}})=-\sum_{t}y_{t}log(\hat{y_{t}})\)
在这里， \(y_{t}\) 是时刻 t 上正确的词， \(\hat{y_{t}}\) 是预测出来的词。我们通常将一整个序列（一个句子）作为一个训练实例，所以总的误差就是各个时刻（词）的误差之和。
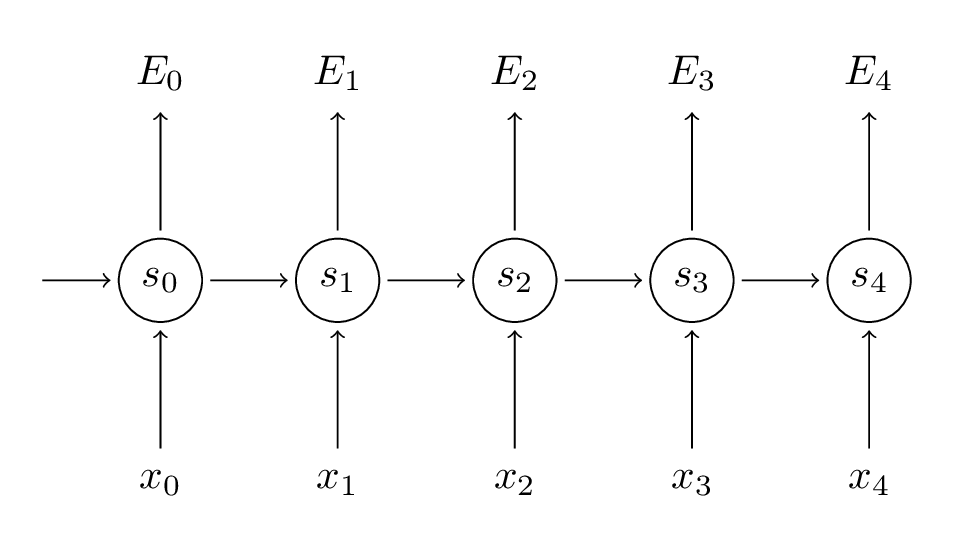
请牢记，我们的目标是计算误差关于参数U、V和W的梯度，然后使用梯度下降法学习出好的参数。正如我们将误差相加，我们也将一个训练实例在每时刻的梯度相加： \(\frac{\partial E}{\partial W} = \sum_{t}\frac{\partial E_{t}}{\partial W}\) 。
为了计算这些梯度，我们需要使用微分的链式法则。当从误差开始向后时，这就是 反向传播 。在本文后续的部分，我们将会以 \(E_{3}\) 为例，仅仅是为了使用具体的数字。
\(\frac{\partial E_{3}}{\partial V} = \frac{\partial E_{3}}{\partial \hat{y_{3}}} \frac{\partial \hat{y_{3}}}{\partial V} =\frac{\partial E_{3}}{\partial \hat{y_{3}}} \frac{\partial \hat{y_{3}}}{\partial z_{3}} \frac{\partial z_{3}}{\partial V}=(\hat{y_{3}} - y_{3}) \otimes s_{3}\)
在上述定义中，我们定义 \(z_{3} = V s_{3}\) ，\(\otimes\) 是两个向量的外积。如果你暂时跟不上，不要担心，我忽略了其中几步，你也可以尝试着自己计算这些梯度。我想要强调的是 \(\frac{\partial E_{3}}{\partial V}\) 仅仅依赖当前时刻的值，如 \(\hat{y_{3}}\) ， \(y_{3}\) ， \(s_{3}\) 。如果你已经有这些值，计算变量V的梯度就是一个简单的矩阵相乘。
计算 \(\frac{\partial E_{3}}{\partial W}\) 却有所不同，对于U也是。为了了解原因，我们写出链式法则，正如上面所示，
\(\frac{\partial E_{3}}{\partial W}=\frac{\partial E_{3}}{\partial \hat{y_{3}}} \frac{\partial \hat{y_{3}}}{\partial s_{3}} \frac{\partial s_{3}}{\partial W}\)
其中， \(s_{3} = tanh(U x_{t} + W s_{2})\) （应该为 \(s_{3} = tanh(U x_{3} + W s_{2})\) ）依赖于 \(s_{2}\) ，而 \(s_{2}\) 依赖于 W和 \(s_{1}\) 。所以如果我们对 W 求导数，我们不能简单的将 \(s_{2}\) 视为一个常量。我们需要再次应用链式法则，我们真正想要的如下所示：
\(\frac{\partial E_{3}}{\partial W}=\sum_{k=0}^{3}\frac{\partial E_{3}}{\partial \hat{y_{3}}} \frac{\partial \hat{y_{3}}}{\partial s_{3}} \frac{\partial s_{3}}{\partial s_{k}} \frac{\partial s_{k}}{\partial W}\)
我们将每时刻对梯度的贡献相加。也就是说，由于 W 在每时刻都用在我们所关心的输出上，我们需要从时刻 t = 3 通过网络的所有路径到时刻 t = 0 来反向传播梯度：
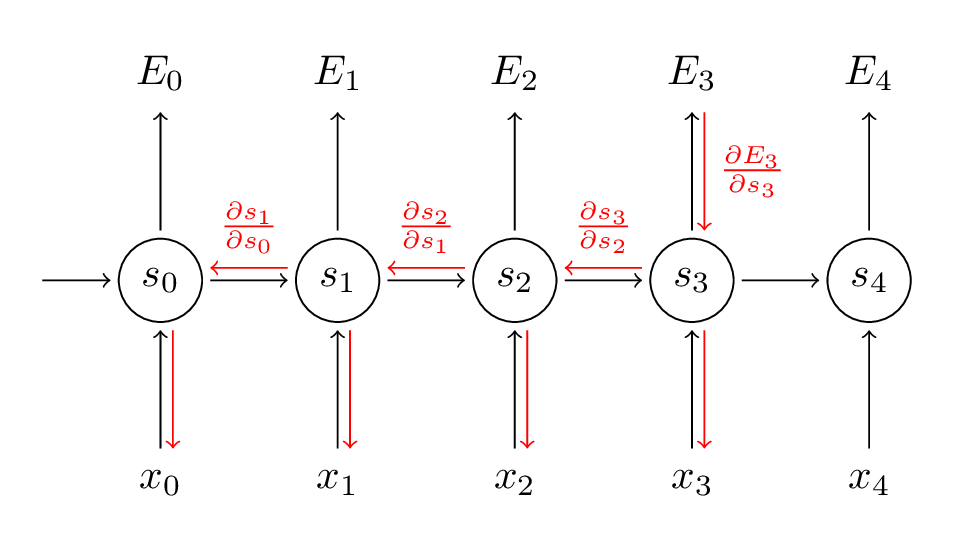
请留意，这与我们在深度前馈神经网络中使用的标准反向传播算法完全相同。主要的差异就是我们将每时刻 W 的梯度相加。在传统的神经网络中，我们在层之间并没有共享参数，所以我们不需要相加。但是我认为，BPTT就是标准反向传播算法在展开的循环神经网络上一个花哨的名称。正如在反向传播算法中，你可以定义一个反向传播的 delta 向量，例如 \(\delta_{2}^{(3)} = \frac{\partial E_{3}}{\partial z_{2}} = \frac{\partial E_{3}}{\partial s_{3}} \frac{\partial s_{3}}{\partial s_{2}} \frac{\partial s_{2}}{\partial z_{2}}\) ，其中 \(z_{2} = U x_{2} + W s_{1}\) ， 然后应用相同的方程。
一个朴素的BPTT实现，代码如下，
def bptt(self, x, y):
T = len(y)
# Perform forward propagation
o, s = self.forward_propagation(x)
# We accumulate the gradients in these variables
dLdU = np.zeros(self.U.shape)
dLdV = np.zeros(self.V.shape)
dLdW = np.zeros(self.W.shape)
delta_o = o
delta_o[np.arange(len(y)), y] -= 1.
# For each output backwards...
for t in np.arange(T)[::-1]:
dLdV += np.outer(delta_o[t], s[t].T)
# Initial delta calculation: dL/dz
delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
# Backpropagation through time (for at most self.bptt_truncate steps)
for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
# print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
# Add to gradients at each previous step
dLdW += np.outer(delta_t, s[bptt_step-1])
dLdU[:,x[bptt_step]] += delta_t
# Update delta for next step dL/dz at t-1
delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
return [dLdU, dLdV, dLdW]
这应该会给你一个印象：为什么标准的循环神经网络很难训练？序列（句子）可以很长，可能20个词或者更多，因此你需要反向传播很多层。实际上，许多人会在反向传播数步之后进行截断。
2 梯度消失
在前面的博文 Recurrent Neural Network系列1--RNN（循环神经网络）概述 中，我已经提到循环神经网络很难学习到长期的依赖 -- 在相隔数步的词之间的影响。这就会导致一些问题，因为英文句子通常被一些不是很近的词所决定，例如：“The man who wore a wig on his head went inside” 。这个句子是关于一个人走进屋里，不是关于假发的。对于普通的循环神经网络，不太可能捕获这些信息。为了理解为什么，让我们仔细分析一下上面推导出来的梯度：
\(\frac{\partial E_{3}}{\partial W}=\sum_{k=0}^{3}\frac{\partial E_{3}}{\partial \hat{y_{3}}} \frac{\partial \hat{y_{3}}}{\partial s_{3}} \frac{\partial s_{3}}{\partial s_{k}} \frac{\partial s_{k}}{\partial W}\)
请注意， \(\frac{\partial s_{3}}{\partial s_{k}}\) 本身就是一个链式法则。例如， \(\frac{\partial s_{3}}{\partial s_{1}} = \frac{\partial s_{3}}{\partial s_{2}} \frac{\partial s_{2}}{\partial s_{1}}\) 。也要注意，我们是在一个向量上对向量函数求导，结果会是一个矩阵（称之为 雅克比矩阵 ），所有的元素都是对应的导数。我可以将上述的梯度重写为：
\(\frac{\partial E_{3}}{\partial W}=\sum_{k=0}^{3}\frac{\partial E_{3}}{\partial \hat{y_{3}}} \frac{\partial \hat{y_{3}}}{\partial s_{3}} (\prod_{j = k+1}^{3} \frac{\partial s_{j}}{\partial s_{j-1}}) \frac{\partial s_{k}}{\partial W}\)
上述雅克比矩阵中的2范数（你可以认为是绝对值）上限是1（具体参考这篇 On the difficulty of training recurrent neural networks）。tanh（或者sigmoid）激活函数将所有的值映射到-1到1这个区间，导数的范围在0到1这个区间（sigmoid是0到 \(\frac{1}{4}\) 这个区间），如下图所示：
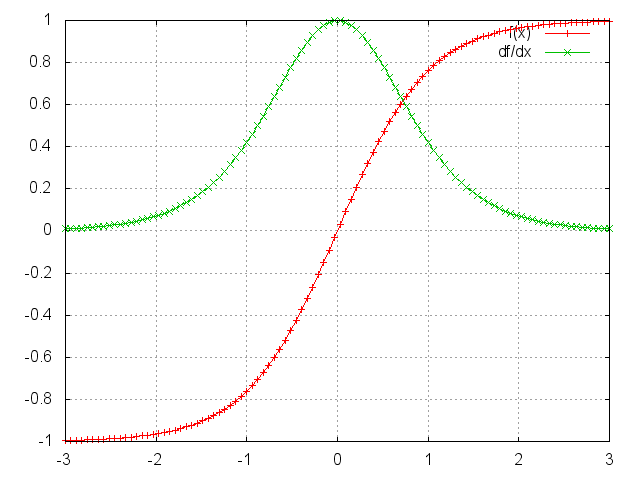
你可以看到tanh和sigmoid函数在两端导数均为0。它们逐渐成为一条直线，当这个现象发生时，我们就说相应的神经元已经饱和了。它们的梯度为0，驱动前一层的其它梯度也趋向于0。因此，矩阵中有小值，并且经过矩阵相乘（t - k次），梯度值快速的以指数形式收缩，最终在几个时刻之后完全消失。较远的时刻贡献的梯度变为0，这些时刻的状态不会对你的学习有所贡献：你最终以无法学习到长期依赖而结束。梯度消失不仅仅出现在循环神经网络中。它们也出现深度前馈神经网络中。它仅仅是循环神经网络趋向于很深（在我们这个例子中，深度与句子长度一样），这将会导致很多问题。
依赖于我们的激活函数和网络参数，如果雅克比矩阵的值非常大，我们没有出现梯度消失，但是却可能出现梯度爆炸。这就是梯度爆炸问题。梯度消失问题比梯度爆炸问题受到更多的关注，主要有两个原因：1）梯度爆炸很明显，你的梯度将会变成Nan（不是一个数字），你的程序将会挂掉；2）在预定义阈值处将梯度截断（具体参考这篇 On the difficulty of training recurrent neural networks）是一种简单有效的方法去解决梯度爆炸问题。梯度消失问题更加复杂是因为它不明显，如论是当它们发生或者如何处理它们时。
幸运的是，目前已经有了一些缓解梯度消失问题的方法。对矩阵 W 合理的初始化可以减少梯度消失的影响。也可以加入正则化项。一个更好的方案是使用 ReLU而不是tanh或者sigmoid激活函数。ReLU函数的导数是个常量，要么是0，要么是1，所以它不太可能出现梯度消失。更加流行的方法是使用长短时记忆（LSTM）或者门控循环单元（GRU）架构。LSTM是在 1997年提出，在NLP领域可能是目前最为流行的模型。GRU是在2014年提出，是LSTM的简化版。这些循环神经网络的设计都是为了处理梯度消失和有效学习长期依赖。我们将会在后面的博文中介绍。
3 Reference
wiki-Backpropagation through time
BPTT算法推导（需要注意此文中W和U与本文的W和U是相反的）
