作者:zhbzz2007 出处:http://www.cnblogs.com/zhbzz2007 欢迎转载,也请保留这段声明。谢谢!
1 算法简介
在 结巴分词2--基于前缀词典及动态规划实现分词 博文中,博主已经介绍了基于前缀词典和动态规划方法实现分词,但是如果没有前缀词典或者有些词不在前缀词典中,jieba分词一样可以分词,那么jieba分词是如何对未登录词进行分词呢?这就是本文将要讲解的,基于汉字成词能力的HMM模型识别未登录词。
利用HMM模型进行分词,主要是将分词问题视为一个序列标注(sequence labeling)问题,其中,句子为观测序列,分词结果为状态序列。首先通过语料训练出HMM相关的模型,然后利用Viterbi算法进行求解,最终得到最优的状态序列,然后再根据状态序列,输出分词结果。
2 实例
2.1 序列标注
序列标注,就是将输入句子和分词结果当作两个序列,句子为观测序列,分词结果为状态序列,当完成状态序列的标注,也就得到了分词结果。
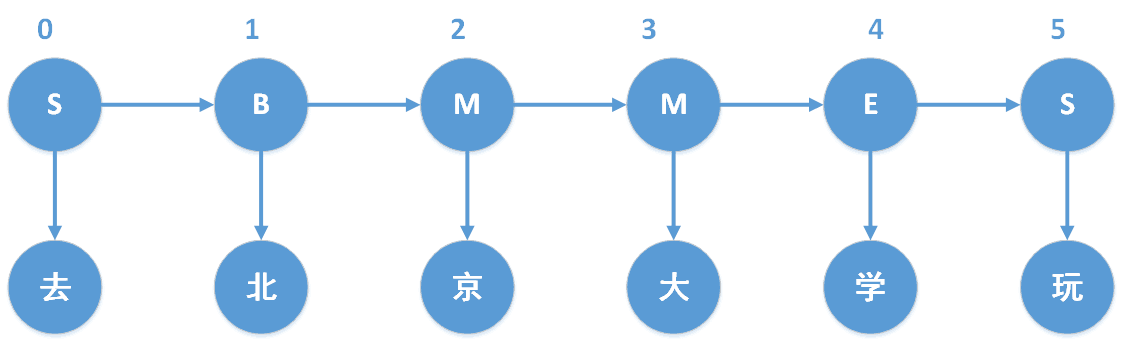
以“去北京大学玩”为例,我们知道“去北京大学玩”的分词结果是“去 / 北京大学 / 玩”。对于分词状态,由于jieba分词中使用的是4-tag,因此我们以4-tag进行计算。4-tag,也就是每个字处在词语中的4种可能状态,B、M、E、S,分别表示Begin(这个字处于词的开始位置)、Middle(这个字处于词的中间位置)、End(这个字处于词的结束位置)、Single(这个字是单字成词)。具体如下图所示,“去”和“玩”都是单字成词,因此状态就是S,“北京大学”是多字组合成的词,因此“北”、“京”、“大”、“学”分别位于“北京大学”中的B、M、M、E。
2.2 HMM模型
关于HMM模型的介绍,网络上有很多的资源,比如 52nlp整理的 HMM相关文章索引 。博主在此就不再具体介绍HMM模型的原理,但是会对分词涉及的基础知识进行讲解。
HMM模型作的两个基本假设:
-
1.齐次马尔科夫性假设,即假设隐藏的马尔科夫链在任意时刻t的状态只依赖于其前一时刻的状态,与其它时刻的状态及观测无关,也与时刻t无关;
P(states[t] | states[t-1],observed[t-1],...,states[1],observed[1]) = P(states[t] | states[t-1]) t = 1,2,...,T
-
2.观测独立性假设,即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其它观测和状态无关,
P(observed[t] | states[T],observed[T],...,states[1],observed[1]) = P(observed[t] | states[t]) t = 1,2,...,T
HMM模型有三个基本问题:
- 1.概率计算问题,给定模型 \(\lambda =(A,B,\pi)\) 和观测序列 \(O=(o_{1},o_{2},...,o_{T})\) ,怎样计算在模型 \(\lambda\) 下观测序列O出现的概率 \(P(O|\lambda)\) ,也就是Forward-backward算法;
- 2.学习问题,已知观测序列 \(O=(o_{1},o_{2},...,o_{T})\) ,估计模型 \(\lambda =(A,B,\pi)\) ,使得在该模型下观测序列的概率 \(P(O|\lambda)\) 尽可能的大,即用极大似然估计的方法估计参数;
- 3.预测问题,也称为解码问题,已知模型 \(\lambda =(A,B,\pi)\) 和观测序列 \(O=(o_{1},o_{2},...,o_{T})\) ,求对给定观测序列条件概率 \(P(S|O)\) 最大的状态序列 \(I=(s_{1},s_{2},...,s_{T})\) ,即给定观测序列。求最有可能的对应的状态序列;
其中,jieba分词主要中主要涉及第三个问题,也即预测问题。
HMM模型中的五元组表示:
- 1.观测序列;
- 2.隐藏状态序列;
- 3.状态初始概率;
- 4.状态转移概率;
- 5.状态发射概率;
这里仍然以“去北京大学玩”为例,那么“去北京大学玩”就是观测序列。
而“去北京大学玩”对应的“SBMMES”则是隐藏状态序列,我们将会注意到B后面只能接(M或者E),不可能接(B或者S);而M后面也只能接(M或者E),不可能接(B或者S)。
状态初始概率表示,每个词初始状态的概率;jieba分词训练出的状态初始概率模型如下所示。其中的概率值都是取对数之后的结果(可以让概率相乘转变为概率相加),其中-3.14e+100代表负无穷,对应的概率值就是0。这个概率表说明一个词中的第一个字属于{B、M、E、S}这四种状态的概率,如下可以看出,E和M的概率都是0,这也和实际相符合:开头的第一个字只可能是每个词的首字(B),或者单字成词(S)。这部分对应jieba/finaseg/prob_start.py,具体可以进入源码查看。
P={'B': -0.26268660809250016,
'E': -3.14e+100,
'M': -3.14e+100,
'S': -1.4652633398537678}
状态转移概率是马尔科夫链中很重要的一个知识点,一阶的马尔科夫链最大的特点就是当前时刻T = i的状态states(i),只和T = i时刻之前的n个状态有关,即{states(i-1),states(i-2),...,states(i-n)}。
再看jieba中的状态转移概率,其实就是一个嵌套的词典,数值是概率值求对数后的值,如下所示,
P={'B': {'E': -0.510825623765990, 'M': -0.916290731874155},
'E': {'B': -0.5897149736854513, 'S': -0.8085250474669937},
'M': {'E': -0.33344856811948514, 'M': -1.2603623820268226},
'S': {'B': -0.7211965654669841, 'S': -0.6658631448798212}}
P['B']['E']代表的含义就是从状态B转移到状态E的概率,由P['B']['E'] = -0.5897149736854513,表示当前状态是B,下一个状态是E的概率对数是-0.5897149736854513,对应的概率值是0.6,相应的,当前状态是B,下一个状态是M的概率是0.4,说明当我们处于一个词的开头时,下一个字是结尾的概率要远高于下一个字是中间字的概率,符合我们的直觉,因为二个字的词比多个字的词更常见。这部分对应jieba/finaseg/prob_trans.py,具体可以查看源码。
状态发射概率,根据HMM模型中观测独立性假设,发射概率,即观测值只取决于当前状态值,也就如下所示,
P(observed[i],states[j]) = P(states[j]) * P(observed[i] | states[j])
其中,P(observed[i] | states[j])就是从状态发射概率中获得的。
P={'B': {'一': -3.6544978750449433,
'丁': -8.125041941842026,
'七': -7.817392401429855,
...
'S': {':': -15.828865681131282,
'一': -4.92368982120877,
'丁': -9.024528361347633,
...
P['B']['一']代表的含义就是状态处于'B',而观测的字是‘一’的概率对数值为P['B']['一'] = -3.6544978750449433。这部分对应jieba/finaseg/prob_emit.py,具体可以查看源码。
2.3 Viterbi算法
Viterbi算法实际上是用动态规划求解HMM模型预测问题,即用动态规划求概率路径最大(最优路径)。这时候,一条路径对应着一个状态序列。
根据动态规划原理,最优路径具有这样的特性:如果最优路径在时刻t通过结点 \(i_{t}^{*}\) ,那么这一路径从结点 \(i_{t}^{*}\) 到终点 \(i_{T}^{*}\) 的部分路径,对于从 \(i_{t}^{*}\) 到 \(i_{T}^{*}\) 的所有可能的部分路径来说,必须是最优的。因为假如不是这样,那么从 \(i_{t}^{*}\) 到 \(i_{T}^{*}\) 就有另一条更好的部分路径存在,如果把它和从 \(i_{t}^{*}\) 到达 \(i_{T}^{*}\) 的部分路径连接起来,就会形成一条比原来的路径更优的路径,这是矛盾的。依据这个原理,我们只需要从时刻t=1开始,递推地计算在时刻t状态i的各条部分路径的最大概率,直至得到时刻t=T状态为i的各条路径的最大概率。时刻t=T的最大概率就是最优路径的概率 \(P^{*}\) ,最优路径的终结点 \(i_{T}^{*}\) 也同时得到。之后,为了找出最优路径的各个结点,从终结点 \(i_{T}^{*}\) 开始,由后向前逐步求得结点 \(i_{T-1}^{*},...,i_{1}^{*}\) ,最终得到最优路径 \(I^{*}=(i_{1}^{*},i_{2}^{*},...,i_{T}^{*})\) 。
2.4 输出分词结果
由Viterbi算法得到状态序列,也就可以根据状态序列得到分词结果。其中状态以B开头,离它最近的以E结尾的一个子状态序列或者单独为S的子状态序列,就是一个分词。以”去北京大学玩“的隐藏状态序列”SBMMES“为例,则分词为”S / BMME / S“,对应观测序列,也就是”去 / 北京大学 / 玩”。
3 源码分析
jieba分词中HMM模型识别未登录词的源码目录在jieba/finalseg/下,
__init__.py 实现了HMM模型识别未登录词;
prob_start.py 存储了已经训练好的HMM模型的状态初始概率表;
prob_trans.py 存储了已经训练好的HMM模型的状态转移概率表;
prob_emit.py 存储了已经训练好的HMM模型的状态发射概率表;
3.1 HMM模型参数训练
HMM模型的参数是如何训练出来,此处可以参考jieba中Issue 模型的数据是如何生成的? #7,如下是jieba的开发者的解释:
来源主要有两个,一个是网上能下载到的1998人民日报的切分语料还有一个msr的切分语料。另一个是我自己收集的一些txt小说,用ictclas把他们切分(可能有一定误差),然后用python脚本统计词频。
要统计的主要有三个概率表:1)位置转换概率,即B(开头),M(中间),E(结尾),S(独立成词)四种状态的转移概率;2)位置到单字的发射概率,比如P("和"|M)表示一个词的中间出现”和"这个字的概率;3) 词语以某种状态开头的概率,其实只有两种,要么是B,要么是S。
3.2 基于HMM模型的分词流程
jieba分词会首先调用函数cut(sentence),cut函数会先将输入句子进行解码,然后调用__cut函数进行处理。__cut函数就是jieba分词中实现HMM模型分词的主函数。__cut函数会首先调用viterbi算法,求出输入句子的隐藏状态,然后基于隐藏状态进行分词。
def __cut(sentence):
global emit_P
# 通过viterbi算法求出隐藏状态序列
prob, pos_list = viterbi(sentence, 'BMES', start_P, trans_P, emit_P)
begin, nexti = 0, 0
# print pos_list, sentence
# 基于隐藏状态序列进行分词
for i, char in enumerate(sentence):
pos = pos_list[i]
# 字所处的位置是开始位置
if pos == 'B':
begin = i
# 字所处的位置是结束位置
elif pos == 'E':
# 这个子序列就是一个分词
yield sentence[begin:i + 1]
nexti = i + 1
# 单独成字
elif pos == 'S':
yield char
nexti = i + 1
# 剩余的直接作为一个分词,返回
if nexti < len(sentence):
yield sentence[nexti:]
3.3 Viterbi算法
首先先定义两个变量, \(\delta,\psi\),定义在时刻t状态i的所有单个路径 \((i_{1},i_{2},...,i_{t})\) 中概率最大值为
\(\delta_{t}(i) = max_{i_{1},i_{2},..,i_{n}}P(i_{t} = i,i_{t-1},...,i_{1},o_{t},...,o_{1}|\lambda), i = 1,2,...,N\)
由此可得变量 \(\delta\) 的递推公式为,
\(\delta_{t+1}(i) = max_{i_{1},i_{2},..,i_{n}}P(i_{t+1} = i,i_{t},...,i_{1},o_{t+1},...,o_{1}|\lambda)\)
\(=max_{1\le j \le N}[\delta_{t}(j)*a_{ji}]*b_{i}(o_{t+1}),i = 1,2,...,N,t = 1,2,...,N-1\)
定义在时刻t状态i的所有单个路径 \((i_{1},i_{2},...,i_{t-1},i)\) 中概率最大的路径的第t-1个结点为,
\(\psi_{t}(i) = argmax_{1 \le j \le N}[\delta_{t-1}(j)*a_{ji}]\)
Viterbi算法的大致流程:
输入:模型 \(\lambda =(A,B,\pi)\) 和观测序列 \(O=(o_{1},o_{2},...,o_{T})\) ;
输出:最优路径 \(I^{*}=(i_{1}^{*},i_{2}^{*},...,i_{T}^{*})\);
(1)初始化
\(\delta_{1}(i) = \pi_{i} * b_{i}(o_{1}),i = 1,2,...,N\)
\(\psi_{1}(i) = 0,i = 1,2,...,N\)
(2)递推
\(\delta_{t}(i) = max_{1\le j \le N}[\delta_{t-1}(j)*a_{ji}]*b_{i}(o_{t}),i = 1,2,...,N\)
\(\psi_{t}(i) = argmax_{1 \le j \le N}[\delta_{t-1}(j)*a_{ji}],,i = 1,2,...,N\)
(3)终止
\(P^{*} = max_{1\le j \le N}\delta_{T}(i)\)
\(i_{T}^{*} = argmax_{1 \le i \le N}[\delta_{T}(i)]\)
(4)最优路径回溯,对于t=T-1,T-2,...,1,
\(i_{t}^{*} = \psi_{t+1}(i)\)
最终求得最优路径 \(I^{*}=(i_{1}^{*},i_{2}^{*},...,i_{T}^{*})\) ;
jieba分词实现Viterbi算法是在viterbi(obs, states, start_p, trans_p, emit_p)函数中实现。viterbi函数会先计算各个初始状态的对数概率值,然后递推计算,每时刻某状态的对数概率值取决于上一时刻的对数概率值、上一时刻的状态到这一时刻的状态的转移概率、这一时刻状态转移到当前的字的发射概率三部分组成。
def viterbi(obs, states, start_p, trans_p, emit_p):
V = [{}] # tabular
path = {}
# 时刻t = 0,初始状态
for y in states: # init
V[0][y] = start_p[y] + emit_p[y].get(obs[0], MIN_FLOAT)
path[y] = [y]
# 时刻t = 1,...,len(obs) - 1
for t in xrange(1, len(obs)):
V.append({})
newpath = {}
# 当前时刻所处的各种可能的状态
for y in states:
# 获取发射概率对数
em_p = emit_p[y].get(obs[t], MIN_FLOAT)
# 分别获取上一时刻的状态的概率对数,该状态到本时刻的状态的转移概率对数,本时刻的状态的发射概率对数
# 其中,PrevStatus[y]是当前时刻的状态所对应上一时刻可能的状态
(prob, state) = max(
[(V[t - 1][y0] + trans_p[y0].get(y, MIN_FLOAT) + em_p, y0) for y0 in PrevStatus[y]])
V[t][y] = prob
# 将上一时刻最优的状态 + 这一时刻的状态
newpath[y] = path[state] + [y]
path = newpath
# 最后一个时刻
(prob, state) = max((V[len(obs) - 1][y], y) for y in 'ES')
# 返回最大概率对数和最优路径
return (prob, path[state])
相关优化:
-
1.将每一时刻最优概率路径记录下来,避免了第4步的最优路径回溯;
-
2.提前建立一个当前时刻的状态到上一时刻的状态的映射表,记录每个状态在前一时刻的可能状态,降低计算量;如下所示,当前时刻的状态是B,那么前一时刻的状态只可能是(E或者S),而不可能是(B或者M);
PrevStatus = {
'B': 'ES',
'M': 'MB',
'S': 'SE',
'E': 'BM'
}



