Loading

从极大似然估计到变分自编码器 - VAE 公式推导

在知乎上也发了一份：https://zhuanlan.zhihu.com/p/711402258

前言

在开始之前，先说说写这篇文章的目的。关于 VAE 的解读和教程已经很多了，但是它们大多是从“逆向工程”的角度出发，作者已经事先知道了 ELBO 这个东西，然后在推导时想办法让公式往 ELBO 上靠。能不能从“正向工程”的角度出发进行推导呢？假设我不了解变分推断和 VAE，怎样从熟悉的极大似然估计出发，一步一步排除掉不合理的设计方案，最终重新发明一遍 VAE 呢?

VAE 的整体思路

VAE 的生成过程有两个步骤：

  1. 隐变量 \(\boldsymbol{z}\) 是根据某个先验分布 \(p(\boldsymbol{z})\) 生成的。
  2. 样本 \(\boldsymbol{x}\) 是从依赖于 \(\boldsymbol{z}\) 的条件分布 \(p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta})\) 生成的。

于是 \(p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta}) = p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta})\) 就是我们所需要的生成模型。

能不能像训练 autoencoder 那样，通过“重构”来训练生成模型呢？一种朴素的想法是：

  1. 生成隐变量 \(\boldsymbol{z}\)。
    • 注：通常会假定隐变量 \(\boldsymbol{z}\) 服从某种简单的概率分布，例如高斯分布，这样只需要简单的随机数生成器就能生成隐变量了。
  2. 根据 \(p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta})\) 从 \(\boldsymbol{z}\) 中生成出（或者说重构出）样本，通过最小化重构损失来训练模型的参数 \(\boldsymbol{\theta}\)。

这个想法的问题在于：我们无法找到生成样本与原始样本之间的对应关系，重构损失算不了，无法训练。

VAE 的做法是引入后验分布 \(p(\boldsymbol{z} | \boldsymbol{x})\)，训练过程变为：

  1. 采样原始样本 \(\boldsymbol{x}\)。
  2. 根据后验分布 \(p(\boldsymbol{z} | \boldsymbol{x})\) 获得每个样本 \(\boldsymbol{x}\) 对应的隐变量 \(\boldsymbol{z}\)。
    • 注：实际上无法算出准确的后验分布，用的是后验分布的一个近似，记为 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\)。
  3. 根据 \(p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta})\) 从隐变量 \(\boldsymbol{z}\) 中重构出 \(\hat{\boldsymbol{x}}\)，通过最小化重构样本 \(\hat{\boldsymbol{x}}\) 与原始样本 \(\boldsymbol{x}\) 的重构损失来训练 \(\boldsymbol{\theta}\)。

从这个角度来看，\(q(\boldsymbol{z} | \boldsymbol{x}; \boldsymbol{\phi})\) 相当于编码器，\(p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta})\) 相当于解码器，训练结束后只需要保留解码器即可，解码器就是我们想要的生成模型。

记号

  • \(\boldsymbol{\theta}\)：生成模型的参数、解码器网络的参数。
  • \(\boldsymbol{\phi}\)：编码器网络的参数。
  • \(\boldsymbol{x}\)：原始样本。
  • \(\hat{\boldsymbol{x}}\)：重构样本。
  • \(\boldsymbol{z}\)：隐变量。
  • \(p(\boldsymbol{z})\)：隐变量的先验 (prior) 分布。
  • \(p(\boldsymbol{z}|\boldsymbol{x})\)：隐变量的后验 (posterior) 分布。
  • \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\)：近似的后验分布。
  • \(p(\boldsymbol{x}; \boldsymbol{\theta})\)：证据 (evidence)、边缘似然 (marginal likelihood)。
  • \(\log p(\boldsymbol{x}; \boldsymbol{\theta})\)：log evidence，很多人会把这个也叫做 evidence。

从极大似然估计开始

接下来，我们将从极大似然估计 (maximum likelihood estimation, MLE) 开始推导 VAE 的优化目标。

在概率论与数理统计中我们就学习过极大似然估计法，它的用途是从数据中估计概率模型的参数。所谓训练一个生成模型，就是给定一堆样本 \(\boldsymbol{x}^{(1)}, \ldots, \boldsymbol{x}^{(N)}\)，从这堆样本中估计出最优的模型参数 \(\boldsymbol{\theta}^*\)，要做的事情其实是一样的。

生成模型的参数记为 \(\boldsymbol{\theta}\)，模型生成样本时的概率密度函数记为 \(p(\boldsymbol{x}; \boldsymbol{\theta})\)，使用极大似然估计法估计模型参数：

\[\begin{aligned} \boldsymbol{\theta}^* & = \operatorname*{\arg\max}_{\boldsymbol{\theta}} p(\boldsymbol{x}^{(1)}; \boldsymbol{\theta}) \cdots p(\boldsymbol{x}^{(N)}; \boldsymbol{\theta}) \\ & = \operatorname*{\arg\max}_{\boldsymbol{\theta}} \log\Big(p(\boldsymbol{x}^{(1)}; \boldsymbol{\theta}) \cdots p(\boldsymbol{x}^{(N)}; \boldsymbol{\theta})\Big) \\ & = \operatorname*{\arg\max}_{\boldsymbol{\theta}} \sum_{i=1}^n \log p(\boldsymbol{x}^{(i)}; \boldsymbol{\theta}). \end{aligned} \]

要是能写出概率密度函数 \(p(\boldsymbol{x}; \boldsymbol{\theta})\) 的表达式，那么用普通的梯度下降就能优化 \(\boldsymbol{\theta}\) 了，我们来试一下。前面提到过，生成模型是一个输入隐变量 \(\boldsymbol{z}\)、输出样本 \(\boldsymbol{x}\) 的神经网络，因此 \(p(\boldsymbol{x}; \boldsymbol{\theta})\) 可以写成积分的形式，如下：

\[\begin{aligned} p(\boldsymbol{x}; \boldsymbol{\theta}) & = \int_{\boldsymbol{z}} p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z} \\ & = \int_{\boldsymbol{z}} p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z}. \end{aligned} \]

现在的问题在于 \(\boldsymbol{z} \to \boldsymbol{x}\) 的过程很复杂，涉及到神经网络，所以概率密度函数 \(p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta})\) 的形式很复杂，这样我们无法解析地求出 \(\int_{\boldsymbol{z}} p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z}\) 这个积分。

采样估计积分

既然解析求解不可行，那么能不能数值求解呢？有经验的同学会注意到，上述积分可以写成期望的形式：

\[\begin{aligned} p(\boldsymbol{x}; \boldsymbol{\theta}) & = \int_{\boldsymbol{z}} p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z} \\ & = \mathbb{E}_{\boldsymbol{z} \sim p(\boldsymbol{z})} [p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})] \\ & \approx \frac{1}{m}\sum_{i=1}^m p(\boldsymbol{x}|\boldsymbol{z}^{(i)}; \boldsymbol{\theta}), \quad \boldsymbol{z}^{(i)} \sim p(\boldsymbol{z}). \end{aligned} \]

于是我们便可以用蒙特卡洛方法，以采样的方式估计积分的值了。对于某个样本 \(\boldsymbol{x}\)，要想估计其概率密度 \(p(\boldsymbol{x}; \boldsymbol{\theta})\)，只需要从先验分布 \(p(\boldsymbol{z})\) 中采样 \(m\) 次 \(\boldsymbol{z}\)，给这 \(m\) 次的 \(p(\boldsymbol{x}|\boldsymbol{z}^{(i)}; \boldsymbol{\theta})\) 算个平均值即可。

问题似乎已经彻底解决了？实则不然，用这种方法估计 \(p(\boldsymbol{x})\) 是非常低效的，采样次数 \(m\) 要设得非常大才能估得比较准。原因在于，对于某个样本 \(\boldsymbol{x}\)，它所“对应”的隐变量 \(\boldsymbol{z}\) 局限在一个很小的区域内。也就是说，只有很少一部分 \(\boldsymbol{z}\) 具有较大的 \(p(\boldsymbol{x}|\boldsymbol{z})\)，绝大部分 \(\boldsymbol{z}\) 对积分的值几乎没有贡献，所以需要大量地采样才能采到那些贡献较大的 \(\boldsymbol{z}\) 点。

普通蒙特卡洛方法的问题在于，忽视了样本 \(\boldsymbol{x}\) 为我们提供的信息，无论是怎样的样本，全都一视同仁地从先验分布 \(p(\boldsymbol{z})\) 中采样。一种改进的思路是运用重要性采样 (importance sampling) 技术，将从先验分布 \(p(\boldsymbol{z})\) 中采样 \(\boldsymbol{z}\) 转化为从后验分布 \(p(\boldsymbol{z}|\boldsymbol{x})\) 中采样 \(\boldsymbol{z}\)：

\[\begin{aligned} p(\boldsymbol{x}; \boldsymbol{\theta}) & = \int_{\boldsymbol{z}} p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z} \\ & = \int_{\boldsymbol{z}} \frac{p(\boldsymbol{z}|\boldsymbol{x})}{p(\boldsymbol{z}|\boldsymbol{x})}p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z} \\ & = \mathbb{E}_{\boldsymbol{z}\sim p(\boldsymbol{z}|\boldsymbol{x})}\left[\frac{p(\boldsymbol{z})p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})}{p(\boldsymbol{z}|\boldsymbol{x})}\right]. \end{aligned} \]

这么做的好处在于后验分布 \(p(\boldsymbol{z}|\boldsymbol{x})\) 是一个尖峰的分布，从中采样得到的 \(\boldsymbol{z}\) 大概率是样本 \(\boldsymbol{x}\) 所“对应”的隐变量，只需要少量采样就能较为准确地估计 \(p(\boldsymbol{x}; \boldsymbol{\theta})\)。

变分推断与 ELBO

那么怎样得到后验分布 \(p(\boldsymbol{z}|\boldsymbol{x})\) 呢，由于

\[p(\boldsymbol{z}|\boldsymbol{x}) = \frac{p(\boldsymbol{z})p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})}{p(\boldsymbol{x}; \boldsymbol{\theta})}, \]

然而 \(p(\boldsymbol{x}; \boldsymbol{\theta})\) 正是我们不知道的、要估计的值，这下死循环了。变分推断 (variational inference, VI) 的破局思路在于，虽然我们不知道真实的后验分布，但是可以用一个模型 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 去近似它。注意，本文开头提到的编码器 \(\boldsymbol{\phi}\) 在这里出现了。于是改为从近似后验分布 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 中采样：

\[\begin{aligned} p(\boldsymbol{x}; \boldsymbol{\theta}) & = \int_{\boldsymbol{z}} p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z} \\ & = \int_{\boldsymbol{z}} \frac{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}p(\boldsymbol{z})p(\boldsymbol{x} | \boldsymbol{z}; \boldsymbol{\theta}) \mathrm{d}\boldsymbol{z} \\ & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\frac{p(\boldsymbol{z})p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right], \end{aligned} \]

改为从近似后验分布 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 中采样后，同样能得到 \(p(\boldsymbol{x}; \boldsymbol{\theta})\) 的一个无偏估计量，近似的好与坏只影响估计量的方差（估计是否高效）。

在变分推断和 VAE 相关文章中，经常能见到 ELBO (evidence lower bound) 这个东西。顾名思义，ELBO 就是 log evidence 的一个下界。\(p(\boldsymbol{x}; \boldsymbol{\theta})\) 这个东西被称为边缘似然 (marginal likelihood)，在变分贝叶斯方法的术语中也被称为证据 (evidence)。可能是出于方便，很多人会把 log evidence 也叫做 evidence，ELBO 当中的 evidence 指的就是 log evidence。

前面说到，利用蒙特卡洛估计和重要性采样方法，我们得到了 evidence 的一个无偏估计量。但是在 VAE 中，并不是直接优化 log evidence 的无偏估计量，而是将 log 放在期望里面：

\[\begin{aligned} \log p(\boldsymbol{x}; \boldsymbol{\theta}) & = \log\mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\frac{p(\boldsymbol{z})p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right] \\ & \geq \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{p(\boldsymbol{z})p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right] \\ & = \text{ELBO}(\boldsymbol{x}; \boldsymbol{\theta}, \boldsymbol{\phi}). \end{aligned} \]

根据琴生不等式，凸/凹函数和期望交换次序时，要变成不等号。VAE 优化的是 log evidence 的一个下界，这个下界就叫做 ELBO。不过，如果我们能以优化的方式最大化 ELBO，那么就可以认为是在间接地最大化 log evidence，从而实现对模型参数 \(\boldsymbol{\theta}\) 的极大似然估计，算是“曲线救国”了。至于为什么优化 ELBO 比优化 \(\log\mathbb{E}[\ldots]\) 更好，详见下一节“ELBO 的优化”。

前面说到，\(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 对真实后验分布 \(p(\boldsymbol{z}|\boldsymbol{x})\) 近似得越好，采样估计的效率就越高。那么怎样让 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 近似得比较好呢，实际上优化 ELBO 可以自动地帮我们实现这一点，注意到 ELBO 可以拆成两项：

\[\begin{aligned} \text{ELBO}(\boldsymbol{x}; \boldsymbol{\theta}, \boldsymbol{\phi}) & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{p(\boldsymbol{x}, \boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right] \\ & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{p(\boldsymbol{x}; \boldsymbol{\theta})p(\boldsymbol{z}|\boldsymbol{x})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right] \\ & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}[\log p(\boldsymbol{x}; \boldsymbol{\theta})] + \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{p(\boldsymbol{z}|\boldsymbol{x})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right] \\ & = \log p(\boldsymbol{x}; \boldsymbol{\theta}) - \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}{p(\boldsymbol{z}|\boldsymbol{x})}\right] \\ & = \log p(\boldsymbol{x}; \boldsymbol{\theta}) - \mathrm{KL}[q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi}) \parallel p(\boldsymbol{z}|\boldsymbol{x})], \end{aligned} \]

因此当我们最大化 ELBO 时，实际上同时干了两件事，一是最大化 log evidence，这是极大似然估计的目标，二是将近似后验分布 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 和真实后验分布 \(p(\boldsymbol{z}|\boldsymbol{x})\) 拉近，以实现更高效的采样估计。不得不说 ELBO 构造得很巧妙，起到了一石二鸟的效果。

这里说一个题外话，细心的朋友可以注意到，此处的 KL 是 reverse KL，而不是更常用的 forward KL，为什么呢？因为无法从真实后验分布中采样，所以只能写成从 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 中采样的 reverse KL 了。VI 和 RL 领域大多用 reverse KL 应该就是出于这个原因——无法从目标分布中采样。注：把目标分布放在第一个位置称为 forward KL，放在第二个位置称为 reverse KL，此处的目标分布是 \(p(\boldsymbol{z}|\boldsymbol{x})\)。

ELBO 的优化

再次将 ELBO 拆分成两项，不过这次的拆分方式稍有不同：

\[\begin{aligned} \text{ELBO}(\boldsymbol{x}; \boldsymbol{\theta}, \boldsymbol{\phi}) & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{p(\boldsymbol{z})p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right] \\ & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}[p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})] + \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{p(\boldsymbol{z})}{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\right] \\ & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}[p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})] - \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}\left[\log\frac{q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}{p(\boldsymbol{z})}\right] \\ & = \mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}[p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})] - \mathrm{KL}[q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi}) \parallel p(\boldsymbol{z})]. \end{aligned} \]

其中第一个积分 \(\mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}[p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})]\) 对应 VAE 的重构损失，第二个积分 \(- \mathrm{KL}[q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi}) \parallel p(\boldsymbol{z})]\) 对应 VAE 的 KL 散度损失。

为什么优化 ELBO 比优化 \(\log\mathbb{E}[\ldots]\) 更好？即为什么要把 log 放到期望里面而不是留在外面。

  1. 除了最大化 log evidence 这个目标，我们还需要一个正则项来拉近 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 和 \(p(\boldsymbol{z}|\boldsymbol{x})\) 的距离，以保证采样估计的高效性，ELBO 相当于自带了 \(-\mathrm{KL}[q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi}) \parallel p(\boldsymbol{z}|\boldsymbol{x})]\) 这个正则项。
  2. 将 log 放到期望里面后，这个积分可以可以拆出 \(-\mathrm{KL}[q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi}) \parallel p(\boldsymbol{z})]\) 这一项，这一项是有解析解的！我们无需采样估计整个积分，只需要对其中的一部分使用采样估计，减少了采样带来的误差。

KL 散度损失

近似后验分布的建模

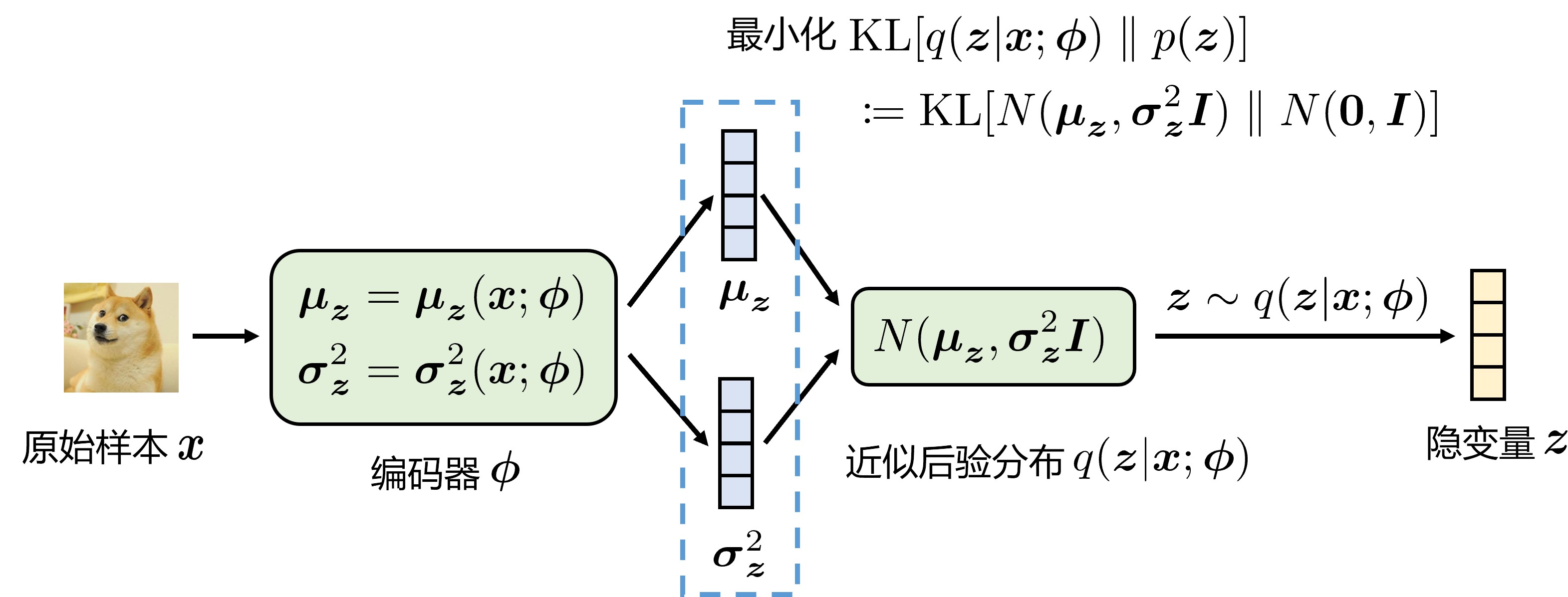
首先面临的问题是如何用神经网络去建模这个近似后验分布 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 呢？平常都是让神经网络输入样本 \(\boldsymbol{x}\) 并输出一个值，但是这里要让神经网络“输出一个分布”。“输出一个分布”听起来有点抽象，其实我们只需要预先定义好某种形式的分布，然后用神经网络输出这个分布的参数即可。VAE 的做法是将近似后验分布建模为各分量相互独立的多元高斯分布

\[q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi}) := N(\boldsymbol{z}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2\boldsymbol{I}), \]

并用编码器网络 \(\boldsymbol{\phi}\) 输出这个高斯分布的参数 \(\boldsymbol{\mu}\) 和 \(\boldsymbol{\sigma}^2\)。

VAE 编码器示意图：

VAE 的编码器部分

KL 散度的解析解

使用各分量相互独立的标准高斯分布作为 \(\boldsymbol{z}\) 的先验分布

\[p(\boldsymbol{z}) := N(\boldsymbol{z}; \boldsymbol{0}, \boldsymbol{I}), \]

这样一来，\(\mathrm{KL}[q(\boldsymbol{z}|\boldsymbol{x}) \parallel p(\boldsymbol{z})]\) 这个积分是可以写出解析解的，无需采样估计。

由于 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 和 \(p(\boldsymbol{z})\) 都是各维度相互独立的，因此只需要推导一维高斯分布的情形即可：

\[\begin{aligned} & \mathrm{KL}[N(z; \mu, \sigma^2) \parallel N(z; 0, 1)] \\ & = \int_z N(z; \mu, \sigma^2)\log\frac{N(z; \mu, \sigma^2)}{N(z; 0, 1)} \mathrm{d}z \\ & = \int_z N(z; \mu, \sigma^2) \log\frac{\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(z - \mu)^2}{2\sigma^2}\right)}{\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{z^2}{2}\right)} \mathrm{d}z \\ & = \int_z N(z; \mu, \sigma^2) \left(-\log\sigma - \frac{(z - \mu)^2}{2\sigma^2} + \frac{z^2}{2} \right) \mathrm{d}z \\ & = \frac{1}{2}\int_z N(z; \mu, \sigma^2) \left(-2\log\sigma - \frac{(z - \mu)^2}{\sigma^2} + z^2\right)\mathrm{d}z \\ & = \frac{1}{2}\left(-\log\sigma^2\int_z N(z; \mu, \sigma^2) \mathrm{d}z - \frac{1}{\sigma^2}\int_z N(z; \mu, \sigma^2)(z - \mu)^2\mathrm{d}z + \int_z N(z; \mu, \sigma^2)z^2\mathrm{d}z\right), \end{aligned} \]

\(\int_z N(z; \mu, \sigma^2) \mathrm{d}z = 1\)，任意概率密度函数在定义域上的积分为 1。

\(\int_z N(z; \mu, \sigma^2)(z - \mu)^2\mathrm{d}z\)，这是方差的定义，高斯分布的方差为 \(\sigma^2\)。

\(\int_z N(z; \mu, \sigma^2)z^2\mathrm{d}z\)，这是二阶矩的定义，高斯分布的二阶矩为 \(\mu^2 + \sigma^2\)。

注：根据方差的常用计算公式 \(\text{Var}[X] = \mathbb{E}[X^2] - \mathbb{E}[X]^2\) 可得 \(\mathbb{E}[X^2] = \mathbb{E}[X]^2 + \text{Var}[X]\)。

所以

\[\begin{aligned} & \mathrm{KL}[N(z; \mu, \sigma^2) \parallel N(z; 0, 1)] \\ & = \frac{1}{2}\left(-\log\sigma^2 \cdot 1 - \frac{1}{\sigma^2} \cdot \sigma^2 + \mu^2 + \sigma^2\right) \\ & = \frac{1}{2}(-\log\sigma^2 - 1 + \mu^2 + \sigma^2). \end{aligned} \]

各维度相互独立时，多维分布的 KL 就是各个维度的 KL 求和：

\[\begin{aligned} & \mathrm{KL}[q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi}) \parallel p(\boldsymbol{z})] \\ & = \int_{\boldsymbol{z}} q(\boldsymbol{z}|\boldsymbol{x})\frac{\log[q(z_1|\boldsymbol{x}) \cdots q(z_J|\boldsymbol{x})]}{\log[p(z_1) \cdots p(z_J)]} \mathrm{d}\boldsymbol{z} \\ & = \int_{\boldsymbol{z}} q(\boldsymbol{z}|\boldsymbol{x}) \left[\sum_{j=1}^J \log q(z_j|\boldsymbol{x}) - \sum_{j=1}^J \log p(z_j)\right] \mathrm{d}\boldsymbol{z} \\ & = \sum_{j=1}^J \int_{\boldsymbol{z}} q(\boldsymbol{z}|\boldsymbol{x})[\log q(z_j|\boldsymbol{x}) - \log p(z_j)] \mathrm{d}\boldsymbol{z} \\ & = \sum_{j=1}^J \int_{z_j} q(z_j|\boldsymbol{x})[\log q(z_j|\boldsymbol{x}) - \log p(z_j)] \mathrm{d}z_j \\ & = \sum_{j=1}^J \mathrm{KL}[q(z_j|\boldsymbol{x}) \parallel p(z_j)], \end{aligned} \]

其中 \(J\) 表示隐变量 \(\boldsymbol{z}\) 的维度。

重构损失

对于 \(\mathbb{E}_{\boldsymbol{z} \sim q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})}[\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})]\) 这个积分，就没有刚才的 KL 项那么好办了。这个积分写不出解析解，只能用采样估计的方法了。不过在实践中，对于每个样本 \(\boldsymbol{x}\)，只需要从 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 采样一次 \(\boldsymbol{z}\) 就能正常训练 VAE 了，效率很高，可见重要性采样的思想还是很有效的。

高斯分布模型作为解码器

接下来解决如何用神经网络建模 \(p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})\) 这个分布的问题。有了刚才建模 \(q(\boldsymbol{z}|\boldsymbol{x}; \boldsymbol{\phi})\) 经验，这里我们依葫芦画瓢，将其建模为各维度独立的高斯分布

\[p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta}) := N(\boldsymbol{x}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2\boldsymbol{I}), \]

解码器网络 \(\boldsymbol{\theta}\) 输入隐变量 \(\boldsymbol{z}\)，输出这个高斯分布的参数 \(\boldsymbol{\mu}\) 和 \(\boldsymbol{\sigma}^2\)。

由于各维度相互独立，因此概率密度函数的表达式为：

\[\begin{aligned} p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta}) & := N(\boldsymbol{x}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2\boldsymbol{I}) \\ & = \prod_{i=1}^D N(x_i; \mu_i, \sigma_i^2) \\ & = \left(\prod_{i=1}^D\frac{1}{\sqrt{2\pi}\sigma_i}\right)\exp\left(\sum_{i=1}^D-\frac{(x_i - \mu_i)^2}{2\sigma_i^2}\right), \end{aligned} \]

其中 \(D\) 表示样本 \(\boldsymbol{x}\) 的维度。

在此基础上，推导一下 \(\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})\) 的表达式：

\[\begin{aligned} & \log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta}) \\ & = -\frac{D}{2}\log 2\pi - \frac{1}{2}\sum_{i=1}^D\log\sigma_i^2 - \frac{1}{2}\sum_{i=1}^D\frac{(x_i - \mu_i)^2}{\sigma_i^2}. \end{aligned} \]

为了简化模型，通常会假设各维度的方差 \(\sigma_i^2\) 都相同，且都是一个常数。此时解码器网络 \(\boldsymbol{\theta}\) 只需要输出均值参数 \(\boldsymbol{\mu}\) 即可，并且有

\[\operatorname*{\arg\max}_{\boldsymbol{\theta}} \log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta}) = \operatorname*{\arg\min}_{\boldsymbol{\theta}} \frac{1}{2}\sum_{i=1}^D(x_i - \mu_i)^2. \]

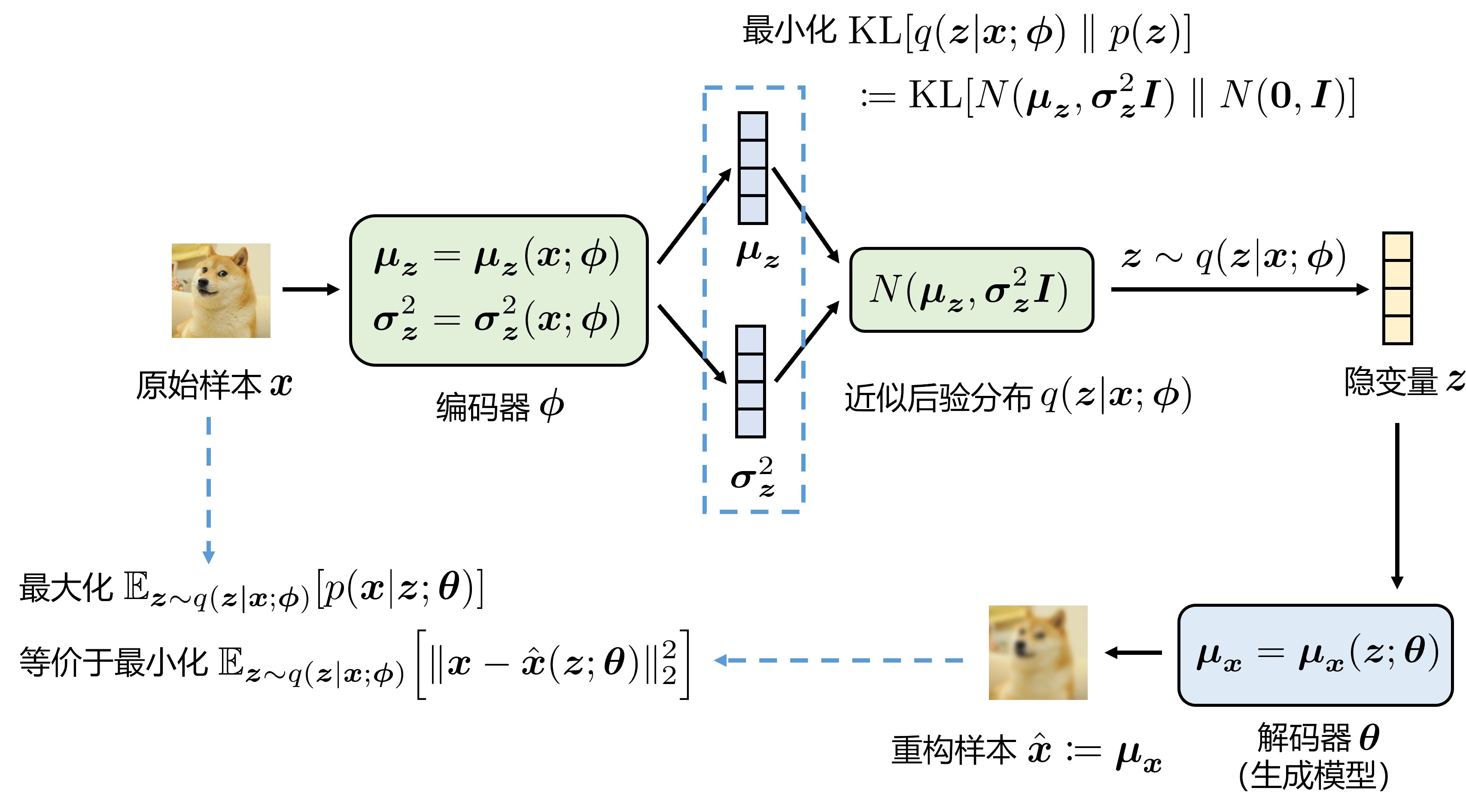
总的来说，如果用高斯分布模型作为解码器，那么：

  1. 解码器网络 \(\boldsymbol{\theta}\) 输出的均值参数 \(\boldsymbol{\mu}\) 就是重构出的样本 \(\hat{\boldsymbol{x}}\)。
  2. 最大化 \(\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})\) 等价于最小化重构样本 \(\hat{\boldsymbol{x}}\) 和原始样本 \(\boldsymbol{x}\) 的 MSE 损失。

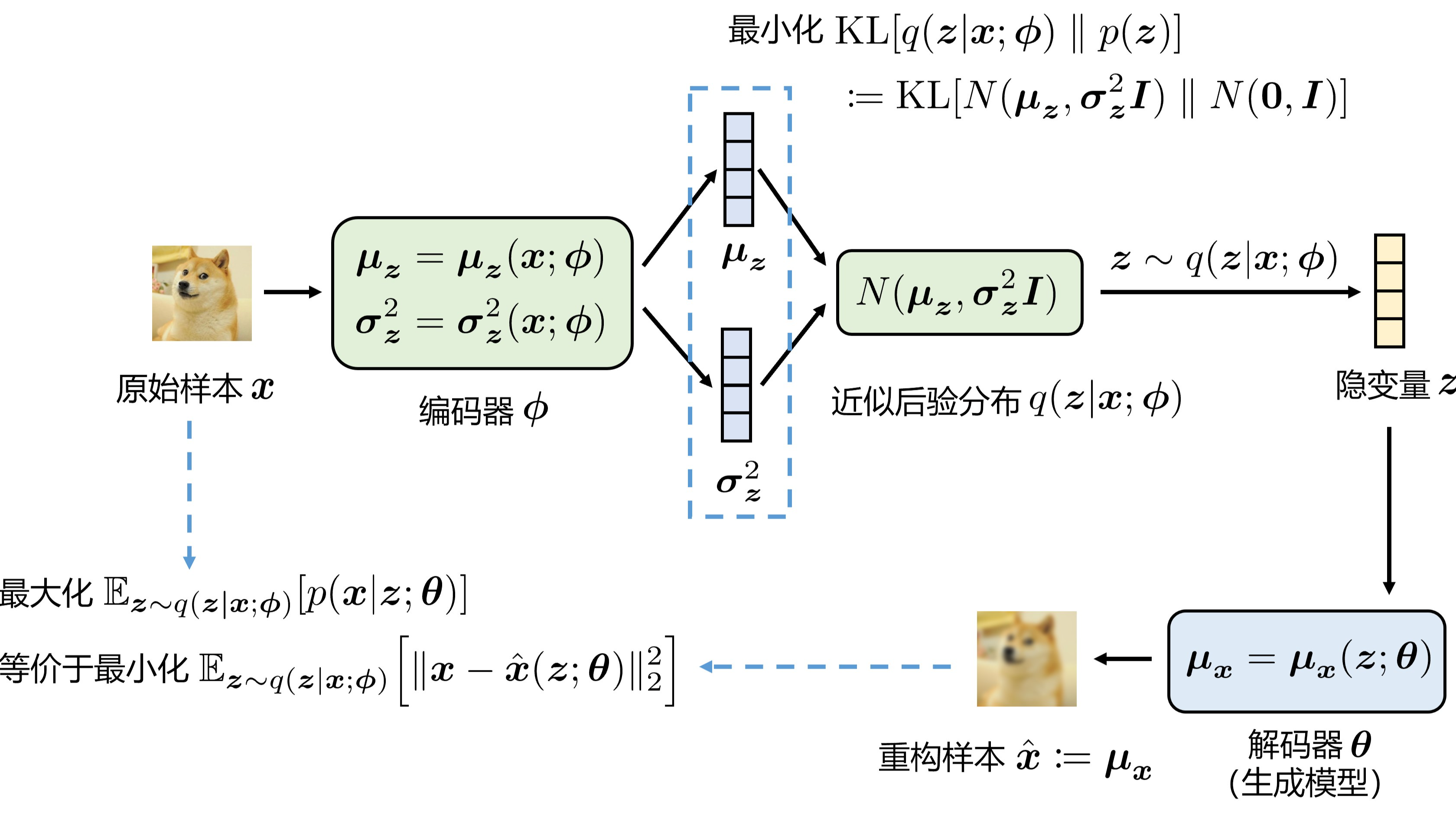
完整的 VAE 示意图：

VAE 示意图

伯努利分布模型作为解码器

有时候样本并不是数值型的，而是离散型的，例如样本可能是 0/1 二值向量，此时不宜使用高斯分布模型作为解码器，而应该使用伯努利分布（两点分布）模型。

类似地，将 \(p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})\) 建模为各维度相互独立的伯努利分布，解码器网络 \(\boldsymbol{\theta}\) 输入隐变量 \(\boldsymbol{z}\)，输出伯努利分布的参数。用 \(y_i\) 表示解码器输出的第 \(i\) 维伯努利分布的参数，有

\[p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta}) := \prod_{i=1}^D y_i^{x_i}(1 - y_i)^{1 - x_i}, \]

\[\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta}) = \sum_{i=1}^D x_i\log y_i + (1 - x_i)\log(1 - y_i). \]

总的来说，如果用伯努利分布模型作为解码器，那么：

  1. 解码器网络 \(\boldsymbol{\theta}\) 输出的参数 \(\boldsymbol{y}\) 就是重构出的样本。
  2. 最大化 \(\log p(\boldsymbol{x}|\boldsymbol{z}; \boldsymbol{\theta})\) 等价于最小化重构样本和原始样本的交叉熵损失。

重参数化技巧实现可微采样

VAE 的编码器与 autoencoder 的编码器不同，autoencoder 的编码器直接输出隐变量 \(\boldsymbol{z}\) 的值，而 VAE 编码器输出的是高斯分布的参数 \(\boldsymbol{\mu}, \boldsymbol{\sigma}^2\)，隐变量 \(\boldsymbol{z}\) 是从分布 \(N(\boldsymbol{z}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2\boldsymbol{I})\) 中采样得到的。

为了通过梯度下降优化编码器网络，需要知道隐变量 \(\boldsymbol{z}\) 对编码器网络 \(\boldsymbol{\phi}\) 的梯度：

\[\frac{\partial\boldsymbol{z}}{\partial\boldsymbol{\phi}} = \frac{\partial\boldsymbol{z}}{\partial\boldsymbol{\mu}}\frac{\partial\boldsymbol{\mu}}{\partial\boldsymbol{\phi}} + \frac{\partial\boldsymbol{z}}{\partial\boldsymbol{\sigma}^2}\frac{\partial\boldsymbol{\sigma}^2}{\partial\boldsymbol{\phi}}, \]

\(\frac{\partial\boldsymbol{\mu}}{\partial\boldsymbol{\phi}}\) 和 \(\frac{\partial\boldsymbol{\sigma}^2}{\partial\boldsymbol{\phi}}\) 很容易求，因为 \(\boldsymbol{\mu}\) 和 \(\boldsymbol{\sigma}^2\) 是编码器网络 \(\boldsymbol{\phi}\) 的直接输出，但是如何计算 \(\frac{\partial\boldsymbol{z}}{\partial\boldsymbol{\mu}}\) 和 \(\frac{\partial\boldsymbol{z}}{\partial\boldsymbol{\sigma}^2}\) 呢，\(\boldsymbol{z}\) 可是由采样得到的。

VAE 的解决方法是所谓的重参数化技巧 (reparameterization trick)，即分布变换，这类方法也叫 pathwise gradient estimator (PGE)。具体而言，为了得到 \(\boldsymbol{z} \sim N(\boldsymbol{z}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2)\)，我们先从无参分布 \(N(\boldsymbol{\epsilon}; \boldsymbol{0}, \boldsymbol{I})\) 中采样一个 \(\boldsymbol{\epsilon}\)，然后通过变换函数 \(\boldsymbol{z} = g(\boldsymbol{\epsilon}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2)\) 得到 \(\boldsymbol{z}\) 即可。这里的变换函数为

\[\boldsymbol{z} = g(\boldsymbol{\epsilon}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2) := \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon}. \]

PGE 的关键思路在于，采样的过程 \(\boldsymbol{\epsilon} \sim N(\boldsymbol{\epsilon}; \boldsymbol{0}, \boldsymbol{I})\) 是与参数 \(\boldsymbol{\mu}, \boldsymbol{\sigma}^2\) 无关的，\(\boldsymbol{z}\) 与参数的关联被挪到了变换函数 \(g(\boldsymbol{\epsilon}; \boldsymbol{\mu}, \boldsymbol{\sigma}^2)\) 之中，所以只要求变换函数 \(g\) 对参数可导即可。

参考资料

论文原文：Auto-Encoding Variational Bayes

15 分钟了解变分推理：

从零推导：变分自编码器（VAE） - Alex的文章 - 知乎

苏剑林的 VAE 系列博客：

posted @ 2023-07-01 13:55  zhb2000  阅读(2042)  评论(0)  编辑  收藏  举报